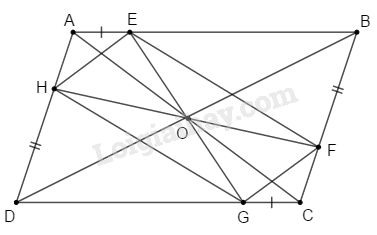
Bài 1 trang 183 SBT toán 8 tập 2

Đề bài

Cho hình bình hành $ABCD.$ $O$ là giao điểm của hai đường chéo. Trên các cạnh $AB, BC, CD, DA$ ta lần lượt lấy các điểm $E, F, G, H$ sao cho $AE = CG, BF = DH.$

a) Xác định tâm đối xứng của hình bình hành $ABCD.$

b) Chứng minh $EFGH$ là hình bình hành, tìm tâm đối xứng của nó.

c) $O$ còn là tâm đối xứng của những hình bình hành nào?

Lời giải chi tiết

a) Tâm đối xứng của hình bình hành $ABCD$ là giao điểm $O$ của hai đường chéo $AC$ và $BD.$

b) $ABCD$ là hình bình hành nên $AB//DC;AD//BC$

Do đó $AE//CG;DH//BF$.

Tứ giác $AECG$ có $AE//CG, AE = CG$ nên $AECG$ là hình bình hành.

$⇒ O$ là trung điểm của $EG.$

Tứ giác $BFDH$ có $BF//DH;BF=DH$ nên $BFDH$ là hình bình hành.

$⇒ O$ là trung điểm của $HF.$

Tứ giác $EFGH$ có hai đường chéo $EG$ và $HF$ cắt nhau tại trung điểm $O$ của mỗi đường nên $EFGH$ là hình bình hành.

Vậy $O$ là tâm đối xứng của hình bình hành $EFGH$.

c) Tứ giác $EBGD$ có hai đường chéo $BD$ và $EG$ cắt nhau tại trung điểm $O$ của mỗi đường nên $EBGD$ là hình bình hành.

Tứ giác $AHCF$ có hai đường chéo $AC$ và $HF$ cắt nhau tại trung điểm $O$ của mỗi đường nên $AHCF$ là hình bình hành.

Vậy $O$ còn là tâm đối xứng của các hình bình hành: $AECG, EBGD, AHCF, BFDH.$

HocTot.Nam.Name.Vn