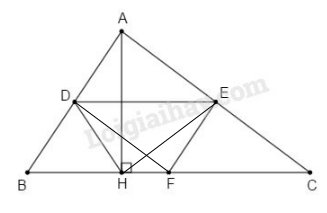
Bài 4 trang 184 SBT toán 8 tập 2

Đề bài

Cho tam giác nhọn \(ABC (AC > AB)\), đường cao \(AH.\) Gọi \(D, E, F\) theo thứ tự là trung điểm của \(AB, AC, BC.\)

a) Xác định dạng của tứ giác \(DECH, BDEF\) và \(DEFH.\)

b) Biết \(AH = 8cm, HB = 4cm,\) \(HC = 6cm,\) tính diện tích các tứ giác \(DECH, BDEF\) và \(DEFH.\)

c) Tính độ dài \(HE.\)

Lời giải chi tiết

a) \(DE\) là đường trung bình của \(\Delta ABC\) nên \(DE//BC;DE = \dfrac{1}{2}BC\).

Tứ giác \(DECH\) có \(DE//HC\) nên  là hình thang.

Tứ giác \(BDEF\) có \(DE//BF; DE=BF= \dfrac{1}{2}BC\) nên là hình bình hành.

Xét tam giác \(AHC\) vuông tại \(H\), có đường trung tuyến \(HE\) ứng với cạnh huyền \(AC\) nên \(HE = \dfrac{1}{2}AC\).

\(DF\) là đường trung bình của \(\Delta ABC\) nên \(DF//AC;DF = \dfrac{1}{2}AC\).

Tứ giác \(DEFH\) có \(DE//HF\) và \(DF = HE = \dfrac{1}{2}AC\) nên là hình thang cân.

b) \(BC=HB+HC=4+6=10 \;(cm)\).

\(BF=FC=DE=BC:2=10:2\)\(\,=5\;(cm)\).

\(HF=BF-BH=5-4=1\;(cm)\).

Hình thang \(DEFH\), hình thang \(DECH\) và hình bình hành \(BDEF\) có cùng chiều cao bằng \(\dfrac{1}{2}AH = \dfrac{1}{2}.8 = 4\,cm\).

Diện tích của hình thang \(DEFH\) là:

\({S_{DEFH}} = \dfrac{1}{2}.\left( {1 + 5} \right).4 = 12\,\left( {c{m^2}} \right)\)

Diện tích hình thang \(DECH\) là:

\({S_{DECH}} = \dfrac{1}{2}.\left( {5 + 6} \right).4 = 22\,\left( {c{m^2}} \right)\)

Diện tích hình bình hành \(BDEF\) là:

\({S_{BDEF}} = 4.5 = 20\,\left( {c{m^2}} \right)\)

c) Áp dụng định lí Pytago vào tam giác vuông \(AHC\), ta có:

\(\begin{array}{l}
A{C^2} = A{H^2} + H{C^2} = {8^2} + {6^2} = 100\\
\Rightarrow AC = \sqrt {100} = 10
\end{array}\)

Suy ra \(HE = \dfrac{1}{2}AC = \dfrac{1}{2}.10 = 5\,\left( {cm} \right)\).

HocTot.Nam.Name.Vn