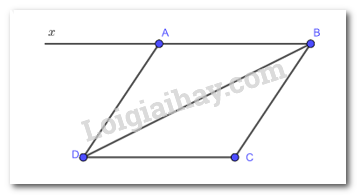
Giải bài 1 trang 107 SGK Toán 8 tập 1 - Cánh diều

Đề bài

Cho tứ giác ABCD có $\widehat {DAB} = \widehat {BC{\rm{D}}};\widehat {ABC} = \widehat {C{\rm{D}}A}$. Kẻ tia Ax là tia đối của tia AB. Chứng minh:

a) $\widehat {ABC} + \widehat {DAB} = {180^o}$

b) $\widehat {xA{\rm{D}}} = \widehat {ABC};AC//BC$

c) Tứ giác ABCD là hình bình hành.

Lời giải chi tiết

a, Tứ giác ABCD có:

$\widehat {ABC} + \widehat {BCD} + \widehat {CDA} + \widehat {DAB} = {360^0}$

$\widehat {ABC} + \widehat {DAB} + \widehat {ABC} + \widehat {DAB} = {360^0}$(do $\widehat {DAB} = \widehat {BCD};\widehat {ABC} = \widehat {CDA}$)

$\begin{array}{l}2\widehat {ABC} + 2\widehat {DAB} = {360^0}\\\widehat {ABC} + \widehat {DAB} = \dfrac{{{{360}^0}}}{2} = {180^0}\end{array}$

b, Ta có: $\widehat {xAD} + \widehat {DAB} = {180^0}$(do tia Ax là tia đối của tia AB)

Nên $\widehat {xAD} + \widehat {DAB} = \widehat {ABC} + \widehat {DAB}$

Suy ra $\widehat {xAD} = \widehat {ABC}$

Suy ra AD//BC (hai góc đồng vị bằng nhau)

c, Vì AD//BC nên $\widehat {ADB} = \widehat {DBC}$ (2 góc so le trong)

Xét $\Delta ADB$ có $\widehat {ABD} = {180^0} - \widehat {ADB} - \widehat {DAB} = {180^0} - \widehat {DBC} - \widehat {BCD}\left( 1 \right)$

(vì $\widehat {ADB} = \widehat {DBC};\widehat {DAB} = \widehat {BCD})$

Xét $\Delta CDB$ có: $\widehat {BDC} = {180^0} - \widehat {DBC} - \widehat {BCD}\left( 2 \right)$

Từ (1), (2) suy ra $\widehat {ABD} =\widehat {BDC}$

Xét $\Delta ADB$ và $\Delta BCD$ có:

$\left. \begin{array}{l}DB \; chung\\\widehat {ABD} = \widehat {BDC}\\\widehat {BAD} = \widehat {DBC}\end{array} \right\}$

Suy ra $\Delta A{\rm{D}}B = \Delta C{\rm{D}}B$

Do đó $A{\rm{D}} = BC,AB = CB$

Suy ra tứ giác ABCD có cặp cạnh đối bằng nhau nên ABCD là hình bình hành.