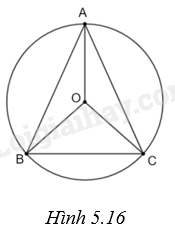
Giải bài 1 trang 105, 106 vở thực hành Toán 9Cho đường tròn (O; 4cm) và ba điểm A, B, C trên đường tròn đó sao cho tam giác ABC cân tại đỉnh A và số đo của cung nhỏ BC bằng ({70^o}). a) Giải thích tại sao hai cung nhỏ AB và AC bằng nhau. b) Tính độ dài của các cung BC, AB và AC (làm tròn kết quả đến hàng phần mười). Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Cho đường tròn (O; 4cm) và ba điểm A, B, C trên đường tròn đó sao cho tam giác ABC cân tại đỉnh A và số đo của cung nhỏ BC bằng \({70^o}\). a) Giải thích tại sao hai cung nhỏ AB và AC bằng nhau. b) Tính độ dài của các cung BC, AB và AC (làm tròn kết quả đến hàng phần mười). Phương pháp giải - Xem chi tiết a) + Chứng minh \(\Delta OAB = \Delta OAC\left( {c.c.c} \right)\). Suy ra \(\widehat {AOB} = \widehat {AOC}\). + Từ đó suy ra hai cung nhỏ $\overset\frown{AB}$ và $\overset\frown{AC}$ bằng nhau. b) + Từ giả thiết \(sđ\overset\frown{BC}={{70}^{o}}\), ta có: Độ dài cung BC là ${{l}_{BC}}=\frac{sđ\overset\frown{BC}}{180}.\pi R$ + Do A thuộc cung lớn BC nên \(sđ\overset\frown{AB}+sđ\overset\frown{AC}=2.sđ\overset\frown{AB}=sđ\overset\frown{BC}\)lớn + Từ đó tính được \(sđ\overset\frown{AB}=sđ\overset\frown{AC}\). + Tính được độ dài mỗi cung nhỏ AB và AC. Lời giải chi tiết (H.5.16) a) Hai tam giác OAB và OAC có: OA là cạnh chung; \(AB = AC\) (\(\Delta ABC\) cân tại A); \(OA = OB\) Do đó, \(\Delta OAB = \Delta OAC\left( {c.c.c} \right)\). Suy ra \(\widehat {AOB} = \widehat {AOC}\). Lại có, cung nhỏ AB bị chắn bởi góc ở tâm \(\widehat {AOB}\); cung nhỏ AC bị chắn bởi góc ở tâm \(\widehat {AOC}\). Từ đó suy ra hai cung nhỏ $\overset\frown{AB}$ và $\overset\frown{AC}$ bằng nhau. b) Từ giả thiết \(sđ\overset\frown{BC}={{70}^{o}}\), ta có: Độ dài cung BC là ${{l}_{BC}}=\frac{sđ\overset\frown{BC}}{180}.\pi R=\frac{70}{180}\pi .4=\frac{14}{9}\pi \approx 4,9\left( cm \right)$ Do A thuộc cung lớn BC nên \(sđ\overset\frown{AB}+sđ\overset\frown{AC}=2.sđ\overset\frown{AB}=sđ\overset\frown{BC}\)lớn$={{360}^{o}}-{{70}^{o}}={{290}^{o}}$ Từ đó ta có \(sđ\overset\frown{AB}=sđ\overset\frown{AC}={{145}^{o}}\). Vậy độ dài mỗi cung nhỏ $\overset\frown{AB}$ và $\overset\frown{AC}$ là: \(l = \frac{{145}}{{180}}\pi .4 = \frac{{29}}{9}\pi \approx 10,1\left( {cm} \right)\)
|