Trang chủ

Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2

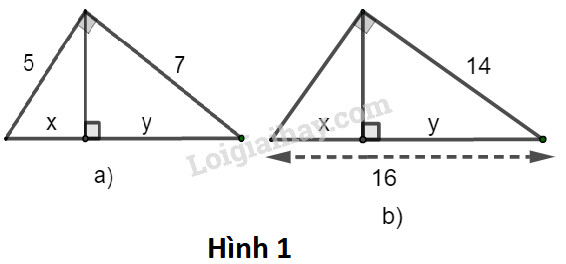
Bài 1 trang 102 SBT toán 9 tập 1

Giải bài 1 trang 102 sách bài tập toán 9. Hãy tính x và y trong các hình sau:

Đề bài

Hãy tính $x$ và $y$ trong các hình sau:

Phương pháp giải - Xem chi tiết

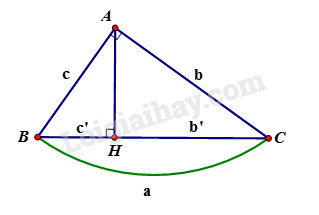
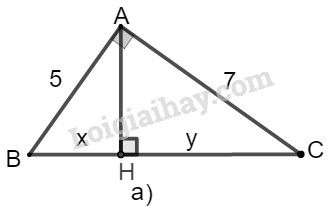
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ . Khi đó ta có các hệ thức sau:

+) $A{B^2} = BH.BC$ hay ${c^2} = a.c'$

+) $A{C^2} = CH.BC$ hay ${b^2} = ab'$

+) $AB^2+AC^2=BC^2$ hay $c^2+b^2=a^2$ (định lý Pytago)

Lời giải chi tiết

a) Ta đặt tên như hình vẽ dưới đây:

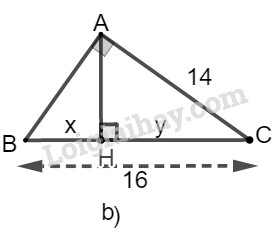
Xét tam giác $ABC$ vuông tại A, đường cao $AH.$

Theo định lý Py-ta-go, ta có:

$B{C^2}=A{C^2}+A{B^2} = {5^2} + {7^2}$

Hay $x + y =BC= \sqrt {{5^2} + {7^2}} = \sqrt {74}$

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó, ta có:

$A{B^2} = BH.BC$

$\Rightarrow {5^2} = x.\sqrt {74} \Rightarrow x = \dfrac{{25}}{{\sqrt {74}}}$

Thay $x = \dfrac{{25}}{{\sqrt {74}}}$ vào $x + y = \sqrt {74}$ , ta có:

$y + \dfrac{{25}}{{\sqrt {74} }} = \sqrt {74}$ $\Rightarrow y = \sqrt {74} - \dfrac{{25}}{{\sqrt {74}}}$ $= \dfrac{{74 - 25}}{{\sqrt {74} }} = \dfrac{{49}}{{\sqrt {74} }}$

Vậy $x = \dfrac{{25}}{{\sqrt {74}}};$ $y= \dfrac{{49}}{{\sqrt {74} }}.$

b) Ta đặt tên như hình vẽ dưới đây:

Xét tam giác $ABC$ vuông tại A, đường cao $AH.$

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:

$A{C^2} = CH.BC$

$\Rightarrow {14^2} = y.16 \Rightarrow y = \dfrac{{{{14}^2}}}{{16}}$ $= \dfrac{{196}}{{16}} = 12,25$

Mà $x + y = 16 \Rightarrow x = 16 - y$ $= 16 - 12,25 = 3,75$

Vậy $x=12,25;y=3,75.$

Chia sẻ

Bình luận

Bình chọn:

4.6 trên 55 phiếu

Bài 2 trang 102 SBT toán 9 tập 1
Giải bài 2 trang 102 sách bài tập toán 9. Hãy tính (x) và (y) trong các hình sau:
Bài 3 trang 103 SBT toán 9 tập 1
Giải bài 3 trang 103 sách bài tập toán 9. Hãy tính x và y trong các hình sau:...
Bài 4 trang 103 SBT toán 9 tập 1
Giải bài 4 trang 103 sách bài tập toán 9. Hãy tính x và y trong các hình sau:
Bài 5 trang 103 SBT toán 9 tập 1
Giải bài 5 trang 103 sách bài tập toán 9. Cho tam giác ABC vuông tại A, đường cao AH (h.5). Giải bài toán trong mỗi trường hợp sau: AH = 16, BH = 25....
Bài 6 trang 103 SBT toán 9 tập 1
Giải bài 6 trang 103 sách bài tập toán 9. Cho tam giác vuông với các cạnh góc vuông có độ dài là 5 và 7, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và các đoạn thẳng và nó chia ra trên cạnh huyền.

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Bài 1 trang 102 SBT toán 9 tập 1

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Góp ý

Báo lỗi góp ý

Báo lỗi