Bài 5 trang 103 SBT toán 9 tập 1

LG a

Cho \(AH = 16, BH = 25.\) Tính \(AB, AC, BC, CH\)

Phương pháp giải:

Để giải bài toán ta áp dụng các công thức sau: 

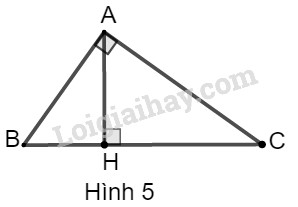
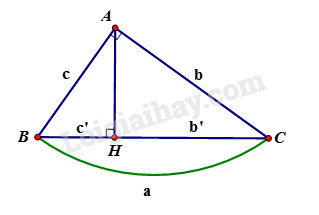
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau:

+) \(A{B^2} = BH.BC\) hay \({c^2} = a.c'\)

+) \(A{C^2} = CH.BC\) hay \({b^2} = ab'\)

+) \(AH^2=HB.HC;AB.AC=AH.BC\)

+) \(AB^2+AC^2=BC^2\) hay \(c^2+b^2=a^2\) (định lý Pytago)

Lời giải chi tiết:

Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: \({AH^2} = BH.CH\)

\( \Rightarrow CH = \dfrac{{A{H^2}}}{{BH}} \)\(=  \dfrac{{{{16}^2}}}{{25}} = 10,24\)

\(BC = BH + CH\)\( = 25 + 10,24 = 35,24\)

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có: 

\(\eqalign{
& A{B^2} = BH.BC \cr 
& \Rightarrow AB = \sqrt {BH.BC} \cr 
& = \sqrt {25.35,24} = \sqrt {881}  \approx  29,68 \cr} \)

\(\eqalign{
& A{C^2} = HC.BC \cr 
& \Rightarrow AC = \sqrt {CH.BC} \cr 
& = \sqrt {10,24.35,24}  \cr 
&= \sqrt {360,9} \approx  18,99 \cr} \) 

LG b

Cho \(AB = 12, BH = 6.\) Tính \(AH, AC, BC, CH.\)

Phương pháp giải:

Để giải bài toán ta áp dụng các công thức sau: 

Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau:

+) \(A{B^2} = BH.BC\) hay \({c^2} = a.c'\)

+) \(A{C^2} = CH.BC\) hay \({b^2} = ab'\)

+) \(AH^2=HB.HC;AB.AC=AH.BC\)

+) \(AB^2+AC^2=BC^2\) hay \(c^2+b^2=a^2\) (định lý Pytago)

Lời giải chi tiết:

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:     

\(\eqalign{
& A{B^2} = BH.BC \cr 
& \Rightarrow BC =  \dfrac{{A{B^2}}}{{BH}} =  \dfrac{{{{12}^2}}}{6} = 24 \cr} \)

\(CH = BC - BH = 24 - 6 = 18\)

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:

\(\eqalign{
& A{C^2} = HC.BC \cr 
& \Rightarrow AC = \sqrt {CH.BC} \cr 
& = \sqrt {18.24} = \sqrt {432} \approx 20,78 \cr} \) 

Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:

\(\eqalign{
& A{H^2} = HB.HC \cr 
& \Rightarrow AH = \sqrt {HB.HC} \cr 
& = \sqrt {6.18} = \sqrt {108} = 6\sqrt 3 \cr} \) 

HocTot.Nam.Name.Vn