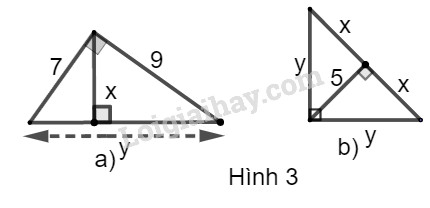
Bài 3 trang 103 SBT toán 9 tập 1Giải bài 3 trang 103 sách bài tập toán 9. Hãy tính x và y trong các hình sau:... Đề bài Hãy tính \(x\) và \(y\) trong các hình sau:
Phương pháp giải - Xem chi tiết
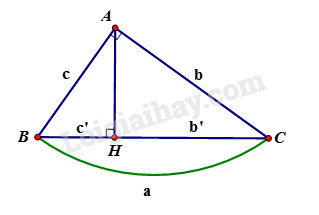
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau: +) \(A{B^2} = BH.BC\) hay \({c^2} = a.c'\) +)\(A{C^2} = CH.BC\) hay \({b^2} = ab'\) +) \(AB^2+AC^2=BC^2\) hay \(c^2+b^2=a^2\) (định lý Pytago) Lời giải chi tiết a) Hình a Theo định lý Pi-ta-go, ta có: \({y^2} = {7^2} + {9^2}\)\( \Rightarrow y = \sqrt {{7^2} + {9^2}} = \sqrt {130} \) Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có: \(x.y = 7.9 \Rightarrow x = \dfrac{{7.9}}{{ y}} = \dfrac{{63}}{{\sqrt {130} }}\) b) Hình b Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: \({5^2} = x.x = {x^2} \Rightarrow x = 5\) Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có: \({y^2} = x.(x + x) = 5.(5 + 5) = 50\)\( \Rightarrow y = \sqrt {50} = 5\sqrt 2 \) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
