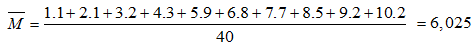Đề thi học kì 2 môn toán lớp 7 năm 2019 - 2020 trường THCS Nguyễn TrãiGiải chi tiết đề thi học kì 2 môn toán lớp 7 năm 2019 - 2020 trường thcs Nguyễn Trãi với cách giải nhanh và chú ý quan trọng
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài I. TRẮC NGHIỆM (1 điểm) Khoanh tròn vào chữ cái A, B, C, D đứng trước câu trả lời đúng trong các câu sau. Câu 1. Giá trị của biểu thức \( - 3{x^2}{y^3}\) tại \(x = - 2\) và \(y = - 1\) là A. \( - 4\) B. \(12\) C. \( - 10\) D. \( - 12\) Câu 2. Bậc của đơn thức \(5{x^3}{y^2}{x^2}z\) là: A. \(3\) B. \(5\) C. \(7\) D. \(8\) Câu 3. Một tam giác có H là trực tâm, thì H là giao điểm của ba đường: A. Đường cao B. Trung trực C. Phân giác D. Trung tuyến Câu 4. Cho tam giác ABC có \(AB = 3\,\,cm,BC = 4\,\,cm,\) \(AC = 5\,\,cm\). Thì: A. Góc A lớn hơn góc B B. Góc B nhỏ hơn góc C C. Góc B lớn hơn góc C D. Góc A nhỏ hơn góc C II. TỰ LUẬN (9 điểm) Bài 1 (1,5 điểm) Điểm kiểm tra học kỳ II môn Toán của lớp 7A được thống kê như sau:
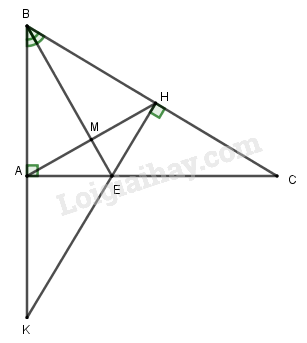
a) Dấu hiệu ở đây là gì? Tìm mốt của dấu hiệu. b) Tìm số trung bình cộng. Bài 2: (3 điểm) Cho hai đa thức \(\begin{array}{l}P\left( x \right) = - 8 + 5x - 5{x^3} + {x^2} - 2{x^4}\\Q\left( x \right) = {x^2} + 8 + 2{x^4} + 5{x^3} - 2x\end{array}\) a) Sắp xếp các đa thức trên theo lũy thừa giảm dần của biến. b) Tính: \(\begin{array}{l}H\left( x \right) = P\left( x \right) + Q\left( x \right)\\F\left( x \right) = P\left( x \right) - Q\left( x \right)\end{array}\) c) Tìm nghiệm của \(H\left( x \right)\). Bài 3: (4 điểm) Cho \(\Delta ABC\) vuông tại \(A\), đường phân giác \(BE\). Kẻ \(EH\) vuông góc với \(BC\) \(\left( {H \in BC} \right)\). Gọi \(K\) là giao điểm của \(AB\) và \(HE\). Chứng minh rằng: a) \(\Delta ABE = \Delta HBE\) b) \(BE\) là đường trung trực của đoạn thẳng \(AH\). c) \(EK = EC\) d) \(AE < EC\) Bài 4: (0,5 điểm) Hãy xác định các hệ số \(a\) và \(b\) để nghiệm của đa thức \(F\left( x \right) = {x^2} + 2x - 15\) cũng là nghiệm của đa thức \(G\left( x \right) = 2{x^2} + ax + b\). Đ/a TN
Câu 1 (NB): Phương pháp: Thay \(x = - 2;y = - 1\) vào biểu thức rồi tính toán Cách giải: Thay \(x = - 2;y = - 1\) vào biểu thức \( - 3{x^2}{y^3}\) ta được: \( - 3.{\left( { - 2} \right)^2}.{\left( { - 1} \right)^3}\) \( = - 3.4.\left( { - 1} \right) = 12\) Chọn B Câu 2 (NB): Phương pháp: Thu gọn đơn thức rồi tìm bậc của đơn thức là tổng số mũ của các biến có trong đơn thức Cách giải: Ta có \(5{x^3}{y^2}{x^2}z\) \( = 5\left( {{x^3}{x^2}} \right){y^2}z = 5{x^5}{y^2}z\) Bậc của đơn thức là \(5 + 2 + 1 = 8\) Chọn D Câu 3 (NB): Phương pháp: Trực tâm là giao điểm của ba đường cao của tam giác Cách giải: Trong một tam giác, trực tâm là giao điểm ba đường cao. Chọn A Câu 4 (TH): Phương pháp: Trong một tam giác, đối diện với cạnh lớn hơn là góc lớn hơn Cách giải: Xét tam giác ABC có \(AC > BC > AB\) \(\left( {5cm > 4cm > 3cm} \right)\) nên \(\widehat B > \widehat A > \widehat C\) (đối diện với cạnh lớn hơn là góc lớn hơn) Chọn C LG bài 1 Phương pháp giải: a) Mốt của dấu hiệu là giá trị có tần số lớn nhất b) Số trung bình cộng: \(\overline M = \dfrac{{{x_1}{n_1} + {x_2}{n_2} + ... + {x_k}{n_k}}}{N}\) Với \({n_1};{n_2};...;{n_k}\) là các tần số tương ứng của các giá trị \({x_1};{x_2};...;{x_k}\) \(N = {n_1} + {n_2} + ... + {n_k}\) là tổng các giá trị Lời giải chi tiết: a) Dấu hiệu ở đây là: Điểm kiểm tra học kỳ II môn Toán của lớp 7A Mốt của dấu hiệu \({M_0} = 5\) (vì giá trị 5 có tần số lớn nhất là 9) b) Số trung bình cộng:
LG bài 2 Phương pháp giải: a) Sắp xếp các đa thức theo yêu cầu b) Thực hiện cộng trừ các đa thức bằng cách cộng trừ các đơn thức đồng dạng c) Nghiệm của đa thức là giá trị của biến làm cho đa thức có giá trị bằng 0 Lời giải chi tiết: a) Ta có: \(\begin{array}{l}P\left( x \right) = - 8 + 5x - 5{x^3} + {x^2} - 2{x^4}\\ = - 2{x^4} - 5{x^3} + {x^2} + 5x - 8\\Q\left( x \right) = {x^2} + 8 + 2{x^4} + 5{x^3} - 2x\\ = 2{x^4} + 5{x^3} + {x^2} - 2x + 8\end{array}\) b) Ta có: \(H\left( x \right) = P\left( x \right) + Q\left( x \right)\) \( = - 2{x^4} - 5{x^3} + {x^2} + 5x - 8\) \( + \left( {2{x^4} + 5{x^3} + {x^2} - 2x + 8} \right)\) \( = - 2{x^4} - 5{x^3} + {x^2} + 5x - 8\) \( + 2{x^4} + 5{x^3} + {x^2} - 2x + 8\) \( = \left( { - 2{x^4} + 2{x^4}} \right) + \left( { - 5{x^3} + 5{x^3}} \right)\) \( + \left( {{x^2} + {x^2}} \right) + \left( {5x - 2x} \right)\)\( - 8 + 8\) \( = 2{x^2} + 3x\) Vậy \(H\left( x \right) = 2{x^2} + 3x\) \(F\left( x \right) = P\left( x \right) - Q\left( x \right)\) \( = - 2{x^4} - 5{x^3} + {x^2} + 5x - 8\) \( - \left( {2{x^4} + 5{x^3} + {x^2} - 2x + 8} \right)\) \( = - 2{x^4} - 5{x^3} + {x^2} + 5x - 8\) \( - 2{x^4} - 5{x^3} - {x^2} + 2x - 8\) \( = \left( { - 2{x^4} - 2{x^4}} \right) + \left( { - 5{x^3} - 5{x^3}} \right)\) \( + \left( {{x^2} - {x^2}} \right) + \left( {5x + 2x} \right)\) \( - 8 - 8\) \( = - 4{x^4} - 10{x^3} + 7x - 16\) Vậy \(F\left( x \right) = - 4{x^4} - 10{x^3} + 7x - 16\) c) Ta có: \(H\left( x \right) = 2{x^2} + 3x\) \(H\left( x \right) = 0\) thì \(2{x^2} + 3x = 0\) \( \Rightarrow x\left( {2x + 3} \right) = 0\) TH1: \(x = 0\) TH2: \(2x + 3 = 0\) \(\begin{array}{l}2x = - 3\\x = - \dfrac{3}{2}\end{array}\) Vậy nghiệm của đa thức \(H\left( x \right)\) là \(x = 0;x = - \dfrac{3}{2}\). LG bài 3 Phương pháp giải: a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền – góc nhọn. b) Chứng minh \(BE\) vuông góc với \(AH\) tại trung điểm của \(AH\) bằng cách gọi \(M\) là giao điểm của \(AH\) với \(BE\). Từ đó chứng minh \(\Delta ABM = \Delta HBM\). c) Chứng minh \(\Delta AEK = \Delta HEC\) theo trường hợp cạnh huyền – cạnh góc vuông. Từ đó suy ra đpcm. d) So sánh \(AE\) và \(EK\) trong cùng tam giác \(AEK\). Từ đó suy ra so sánh \(AE\) và \(EC\) (chú ý \(EK = EC\)) Lời giải chi tiết: Cho \(\Delta ABC\) vuông tại \(A\), đường phân giác \(BE\). Kẻ \(EH\) vuông góc với \(BC\) \(\left( {H \in BC} \right)\). Gọi \(K\) là giao điểm của \(AB\) và \(HE\). Chứng minh rằng:
a) \(\Delta ABE = \Delta HBE\) Tam giác \(ABC\) vuông tại \(A\) nên \(\widehat {BAE} = {90^0}\) \(EH \bot BC\left( {gt} \right)\) \( \Rightarrow \widehat {EHB} = {90^0}\) Xét \(\Delta ABE\) và \(\Delta HBE\) có: \(\widehat {BAE} = \widehat {EHB} = {90^0}\) \(\widehat {ABE} = \widehat {HBE}\) (\(BE\) là phân giác góc \(B\)) \(BE\) chung \( \Rightarrow \Delta ABE = \Delta HBE\left( {ch - gn} \right)\) (đpcm) b) \(BE\) là đường trung trực của đoạn thẳng \(AH\). Gọi \(M\) là giao điểm của \(BE\) và \(AH\). Theo câu a, \(\Delta ABE = \Delta HBE\)\( \Rightarrow AB = HB\) (cạnh tương ứng) Xét \(\Delta ABM\) và \(\Delta HBM\) có: \(\begin{array}{l}AB = HB\left( {cmt} \right)\\\widehat {ABM} = \widehat {HBM}\left( {cmt} \right)\\BM\,\,\,chung\\ \Rightarrow \Delta ABM = \Delta HBM\left( {c - g - c} \right)\end{array}\) \( \Rightarrow AM = HM\) (cạnh tương ứng) \(\widehat {AMB} = \widehat {HMB}\) (góc tương ứng) Mà \(\widehat {AMB} + \widehat {HMB} = {180^0}\) (kề bù) \( \Rightarrow 2\widehat {AMB} = {180^0} \Rightarrow \widehat {AMB} = {90^0}\) \( \Rightarrow BM \bot AH\) Do đó \(BE\) vuông góc với \(AH\) tại trung điểm \(M\). Vậy \(BE\) là đường trung trực của đoạn thẳng \(AH\) (đpcm). c) \(EK = EC\) Theo câu a, \(\Delta ABE = \Delta HBE\)\( \Rightarrow AE = HE\) (cạnh tương ứng) Xét \(\Delta AEK\) và \(\Delta HEC\) có: \(\begin{array}{l}\widehat {EAK} = \widehat {EHC} = {90^0}\\EA = EH\left( {cmt} \right)\end{array}\) \(\widehat {AEK} = \widehat {HEC}\) (đối đỉnh) \( \Rightarrow \Delta AEK = \Delta HEC\left( {ch - cgv} \right)\) \( \Rightarrow EK = EC\) (cạnh tương ứng) (đpcm) d) \(AE < EC\) Xét tam giác \(AEK\) có \(\widehat {EAK} = {90^0}\) nên \(\widehat {AKE} < \widehat {EAK}\) \( \Rightarrow AE < EK\) (quan hệ giữa góc và cạnh đối diện trong tam giác) Mà \(EK = EC\left( {cmt} \right)\) nên \(AE < EC\) (đpcm). LG bài 4 Phương pháp giải: - Tìm nghiệm của đa thức \(F\left( x \right)\). - Thay nghiệm này vào đa thức \(G\left( x \right)\) suy ra \(a,b\). Lời giải chi tiết: Hãy xác định các hệ số \(a\) và \(b\) để nghiệm của đa thức \(F\left( x \right) = {x^2} + 2x - 15\) cũng là nghiệm của đa thức \(G\left( x \right) = 2{x^2} + ax + b\). Ta có: \(\begin{array}{l}{x^2} + 2x - 15\\ = {x^2} + 5x - 3x - 15\\ = \left( {{x^2} + 5x} \right) - \left( {3x + 15} \right)\\ = x\left( {x + 5} \right) - 3\left( {x + 5} \right)\\ = \left( {x - 3} \right)\left( {x + 5} \right)\end{array}\) \(\begin{array}{l}F\left( x \right) = 0\\ \Rightarrow \left( {x - 3} \right)\left( {x + 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x + 5 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 5\end{array} \right.\end{array}\) Do đó đa thức \(F\left( x \right)\) có các nghiệm là \(3\) và \( - 5\). Để các nghiệm \(3\) và \( - 5\) cũng là nghiệm của \(G\left( x \right)\) thì: \(\begin{array}{l}{2.3^2} + a.3 + b = 0\\ \Leftrightarrow 18 + 3a + b = 0\\ \Leftrightarrow b = - 18 - 3a\end{array}\) Và \(\begin{array}{l}2.{\left( { - 5} \right)^2} + a.\left( { - 5} \right) + b = 0\\ \Leftrightarrow 50 - 5a + b = 0\\ \Rightarrow 50 - 5a + \left( { - 18 - 3a} \right) = 0\\ \Leftrightarrow 50 - 5a - 18 - 3a = 0\\ \Leftrightarrow 32 - 8a = 0\\ \Leftrightarrow 8a = 32\\ \Leftrightarrow a = 4\\ \Rightarrow b = - 18 - 3.4 = - 30\end{array}\) Vậy \(a = 4,b = - 30\). HẾT HocTot.Nam.Name.Vn
|