Đề thi học kì 2 môn toán lớp 7 năm 2019 - 2020 PGD Thành phố HuếGiải chi tiết đề thi học kì 2 môn toán lớp 7 năm 2019 - 2020 PGD thành phố Huế với cách giải nhanh và chú ý quan trọng
Lựa chọn câu để xem lời giải nhanh hơn
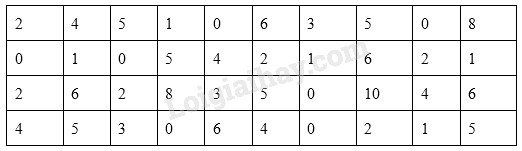
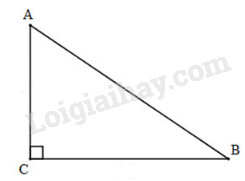
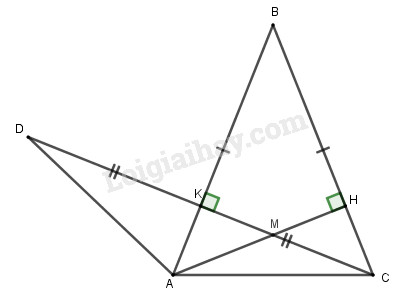
Đề bài Bài 1 (1,5 điểm): Cho hai đơn thức: \(A = 6{y^3}z.\left( { - \dfrac{2}{3}{x^2}yz} \right)\) và \(B = {\left( {2xy} \right)^2}.\dfrac{3}{5}{y^2}{z^2}.\) Chứng tỏ hai đơn thức trên đồng dạng Bài 2 (1,0 điểm): a) Cho \(\Delta ABC\) vuông tại C có \(AB = 25cm,AC = 15cm.\) Tính độ dài cạnh BC. b) Cho \(\Delta MNP\) có \(\widehat M = {50^0};\widehat P = {70^0}.\) So sánh MP với MN. Bài 3 (2,5 điểm): Số buổi vắng của từng học sinh trong HK1 ở lớp 7/1 dược ghi lại như sau:
a) Dấu hiệu ở đây là gì? Lớp 7/1 có bao nhiêu học sinh? b) Lập bảng tần số, tính số trung bình cộng (làm tròn đến hàng đơn vị) và tìm mốt của dấu hiệu. Bài 4 (2,0 điểm): Cho hai đa thức \(M\left( x \right) = 4{x^2} - 3{x^4} + {x^3} - 2{x^2} + {x^4} + 8\) \(N\left( x \right) = {x^4} + 2{x^3} - 2{x^2} - 3{x^3} + x + 6\) a) Thu gọn và sắp xếp các đa thức \(M\left( x \right),N\left( x \right)\) theo lũy thừa giảm dần của biến b) Tìm bậc, hệ số tự do, hệ số cao nhất của đa thức \(P\left( x \right) = M\left( x \right) - N\left( x \right)\) c) Chứng tỏ \(x = 2\) là nghiệm của đa thức \(H\left( x \right) = M\left( x \right) + N\left( x \right)\) Bài 5 (3,0 điểm): Cho \(\Delta ABC\) cân tại B \(\left( {\widehat B < {{90}^0}} \right)\). Kẻ \(AH \bot BC\left( {H \in BC} \right),\) \(CK \bot AB\left( {K \in AB} \right)\), AH và CK cắt nhau tại M a) Chứng minh AH=CK b) Chứng minh \(\Delta MAC\) cân c) Trên tia CK lấy điểm D sao cho K là trung điểm của CD. Chứng minh \(\widehat {ADC} = \widehat {HAC}.\) HẾT LG bài 1 Phương pháp giải: Thực hiện nhân để thu gọn các đơn thức sau đó chứng minh hai đơn thức đồng dạng bằng cách chỉ ra phần hệ số khác 0 và phần biến số giống nhau Lời giải chi tiết: Ta có: \(A = 6{y^3}z.\left( { - \dfrac{2}{3}{x^2}yz} \right)\)\( = \left( {6.\dfrac{{ - 2}}{3}} \right).\left( {{y^3}.y} \right).\left( {z.z} \right).{x^2}\) \( = - 4{x^2}{y^4}{z^2}\) \(B = {\left( {2xy} \right)^2}.\dfrac{3}{5}{y^2}{z^2}\)\( = 4.{x^2}{y^2}.\dfrac{3}{5}{y^2}{z^2}\) \( = \left( {4.\dfrac{3}{5}} \right).{x^2}.\left( {{y^2}.{y^2}} \right).{z^2}\) \( = \dfrac{{12}}{5}.{x^2}{y^4}{z^2}\) Hai đa thức trên có phần hệ số khác 0 và phần biến số giống nhau (cùng là \({x^2}{y^4}{z^2}\)) nên chúng là hai đơn thức đồng dạng. LG bài 2 Phương pháp giải: a) Sử dụng định lý Pytago trong tam giác vuông: Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông b) Sử dụng: Trong một tam giác, đối diện với góc lớn hơn là cạnh lớn hơn. Lời giải chi tiết: a) Cho \(\Delta ABC\) vuông tại C có \(AB = 25cm,AC = 15cm.\) Tính độ dài cạnh BC.
Xét tam giác ABC vuông tại C, theo định lý Pytago ta có: \(\begin{array}{l}A{B^2} = A{C^2} + B{C^2}\\ \Rightarrow B{C^2} = A{B^2} - A{C^2}\end{array}\) \( = {25^2} - {15^2} = 400\) \( \Rightarrow BC = 20cm\) Vậy BC=20cm b) Cho \(\Delta MNP\) có \(\widehat M = {50^0};\widehat P = {70^0}.\) So sánh MP với MN. Xét tam giác MNP, theo định lý tổng ba góc trong tam giác ta có: \(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^0}\\ \Rightarrow \widehat N = {180^0} - \widehat M - \widehat P\\ = {180^0} - {50^0} - {70^0} = {60^0}\end{array}\) Hay \(\widehat N = {60^0}\) Trong \(\Delta MNP\) có \(\widehat N < \widehat P\) (do \({60^0} < {70^0}\)) Nên \(MP < MN\) (đối diện với góc nhỏ hơn là cạnh nhỏ hơn) LG bài 3 Phương pháp giải: a) Dựa vào bảng số liệu xác định dấu hiệu và số học sinh lớp 7/1 b) Tần số của 1 giá trị là số lần xuất hiện của nó trong bảng số liệu Mốt của dấu hiệu là giá trị có tần số cao nhấ Số trung bình cộng: \(\overline M = \dfrac{{{x_1}{n_1} + {x_2}{n_2} + ... + {x_k}{n_k}}}{N}\) Với \({n_1};{n_2};...;{n_k}\) là các tần số tương tứng của các giá trị \({x_1};{x_2};...;{x_k}\) \(N = {n_1} + {n_2} + ... + {n_k}\) là tổng các tần số Lời giải chi tiết: a) Dấu hiệu ở đây là số buổi vắng của từng học sinh trong HK1 ở lớp 7/1 Lớp 7/1 có 40 học sinh (vì bảng số liệu có tất cả 40 giá trị) b) Bảng tần số:
Số trung bình cộng: \(\overline M = \dfrac{{0.7 + 1.5 + 2.6 + 3.3 + 4.5 + 5.6 + 6.5 + 8.2 + 10.1}}{{40}}\) \( = 3,3 \approx 3\). Mốt của dấu hiệu là \({M_0} = 0\) (vì giá trị 0 có tần số lớn nhất là 7) LG bài 4 Phương pháp giải: a) Nhóm các đơn thức đồng dạng và thức hiện phép cộng, trừ các đơn thức đó. b) Thực hiện tính \(M\left( x \right) - N\left( x \right)\) rồi thu gọn được đa thức \(P\left( x \right)\). c) Tính \(H\left( x \right)\), kiểm tra \(H\left( 2 \right) = 0\) rồi suy ra kết luận. Lời giải chi tiết: a) \(\begin{array}{l}M\left( x \right)\\ = 4{x^2} - 3{x^4} + {x^3} - 2{x^2} + {x^4} + 8\\ = \left( {4{x^2} - 2{x^2}} \right) - \left( {3{x^4} - {x^4}} \right) + {x^3} + 8\\ = 2{x^2} - 2{x^4} + {x^3} + 8\\ = - 2{x^4} + {x^3} + 2{x^2} + 8\\N\left( x \right)\\ = {x^4} + 2{x^3} - 2{x^2} - 3{x^3} + x + 6\\ = {x^4} + \left( {2{x^3} - 3{x^3}} \right) - 2{x^2} + x + 6\\ = {x^4} - {x^3} - 2{x^2} + x + 6\end{array}\) Vậy \(\begin{array}{l}M\left( x \right) = - 2{x^4} + {x^3} + 2{x^2} + 8\\N\left( x \right) = {x^4} - {x^3} - 2{x^2} + x + 6\end{array}\) b) \(\begin{array}{l}M\left( x \right) - N\left( x \right)\\ = - 2{x^4} + {x^3} + 2{x^2} + 8\\ - \left( {{x^4} - {x^3} - 2{x^2} + x + 6} \right)\\ = - 2{x^4} + {x^3} + 2{x^2} + 8\\ - {x^4} + {x^3} + 2{x^2} - x - 6\\ = \left( { - 2{x^4} - {x^4}} \right) + \left( {{x^3} + {x^3}} \right)\\ + \left( {2{x^2} + 2{x^2}} \right) - x + \left( {8 - 6} \right)\\ = - 3{x^4} + 2{x^3} + 4{x^2} - x + 2\end{array}\) Do đó \(P\left( x \right) = - 3{x^4} + 2{x^3} + 4{x^2} - x + 2\) Bậc của \(P\left( x \right)\) là \(4\). Hệ số tự do của \(P\left( x \right)\) là \(2\). Hệ số cao nhất của \(P\left( x \right)\) là \( - 3\). c) \(\begin{array}{l}M\left( x \right) + N\left( x \right)\\ = - 2{x^4} + {x^3} + 2{x^2} + 8\\ + \left( {{x^4} - {x^3} - 2{x^2} + x + 6} \right)\\ = - 2{x^4} + {x^3} + 2{x^2} + 8\\ + {x^4} - {x^3} - 2{x^2} + x + 6\\ = \left( { - 2{x^4} + {x^4}} \right) + \left( {{x^3} - {x^3}} \right)\\ + \left( {2{x^2} - 2{x^2}} \right) + x + \left( {8 + 6} \right)\\ = - {x^4} + x + 14\\ \Rightarrow H\left( x \right) = - {x^4} + x + 14\end{array}\) Với \(x = 2\) thì \(H\left( 2 \right) = - {2^4} + 2 + 14\) \( = - 16 + 2 + 14 = 0\) \( \Rightarrow H\left( 2 \right) = 0\) Vậy \(x = 2\) là một nghiệm của đa thức \(H\left( x \right)\). LG bài 5 Phương pháp giải: a) Chứng minh \(\Delta AHB = \Delta CKB\) theo trường hợp cạnh huyền – góc nhọn. b) Chứng minh tam giác có hai góc kề một đáy bằng nhau. c) Chứng minh \(\widehat {ADC} = \widehat {ACK}\) rồi sử dụng tính chất bắc cầu suy ra đpcm. Lời giải chi tiết: Cho \(\Delta ABC\) cân tại B \(\left( {\widehat B < {{90}^0}} \right)\). Kẻ \(AH \bot BC\left( {H \in BC} \right),\) \(CK \bot AB\left( {K \in AB} \right)\), AH và CK cắt nhau tại M
a) Chứng minh AH=CK Tam giác ABC cân tại B nên BA=BC. \(AH\) là đường cao của tam giác nên \(\widehat {AHB} = {90^0}\) \(CK\) là đường cao của tam giác nên \(\widehat {CKB} = {90^0}\) Xét \(\Delta AHB\) và \(\Delta CKB\) có: \(\widehat {AHB} = \widehat {CKB} = {90^0}\) \(\begin{array}{l}AB = CB\left( {cmt} \right)\\\widehat B\,\,\,chung\end{array}\) \( \Rightarrow \Delta AHB = \Delta CKB\) (cạnh huyền – góc nhọn) \( \Rightarrow AH = CK\) (cạnh tương ứng) (đpcm). b) Chứng minh \(\Delta MAC\) cân Tam giác ABC cân tại B nên \(\widehat {BAC} = \widehat {BCA}\) (1) Theo câu a, \(\Delta AHB = \Delta CKB\)\( \Rightarrow \widehat {BAH} = \widehat {BCK}\) (2) Từ (1) và (2) suy ra \(\begin{array}{l}\widehat {BAC} - \widehat {BAH} = \widehat {BCA} - \widehat {BCK}\\ \Rightarrow \widehat {HAC} = \widehat {KCA}\\ \Rightarrow \widehat {MAC} = \widehat {MCA}\end{array}\) Tam giác \(MAC\) có \(\widehat {MAC} = \widehat {MCA}\left( {cmt} \right)\) nên là tam giác cân tại \(M\) (đpcm) c) Trên tia CK lấy điểm D sao cho K là trung điểm của CD. Chứng minh \(\widehat {ADC} = \widehat {HAC}.\) Xét \(\Delta AKD\) và \(\Delta AKC\) có: \(\begin{array}{l}\widehat {AKD} = \widehat {AKC} = {90^0}\\AK\,\,chung\\KD = KC\left( {gt} \right)\end{array}\) \( \Rightarrow \Delta AKD = \Delta AKC\) (2 cạnh góc vuông) \( \Rightarrow \widehat {ADK} = \widehat {ACK}\) (góc tương ứng) Mà \(\widehat {ACK} = \widehat {HAC}\left( {cmt} \right)\) nên \(\widehat {ADK} = \widehat {HAC}\left( { = \widehat {ACK}} \right)\) \( \Rightarrow \widehat {ADC} = \widehat {HAC}\) (đpcm) HẾT HocTot.Nam.Name.Vn
|