Đề thi học kì 1 Toán 10 Cánh diều - Đề số 2Tải về Câu 1: Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x - 4y + 12 \ge 0}\\{x + y - 5 \ge 0}\\{x + 1 > 0}\end{array}} \right.\)là miền chứa điểm nào trong các điểm sau?
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài I. Phần trắc nghiệm Câu 1: Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x - 4y + 12 \ge 0}\\{x + y - 5 \ge 0}\\{x + 1 > 0}\end{array}} \right.\)là miền chứa điểm nào trong các điểm sau? A. \(M\left( {1{\mkern 1mu} ;{\mkern 1mu} - 3} \right)\) B. \(N\left( {4{\mkern 1mu} ;{\mkern 1mu} 3} \right)\). C. \(P\left( { - 1{\mkern 1mu} ;{\mkern 1mu} 5} \right)\). D. \(Q\left( { - 2{\mkern 1mu} ;{\mkern 1mu} - 3} \right)\). Câu 2: Tìm tập xác định D của hàm số \(y = \frac{{3x - 1}}{{2x - 2}}\). A. \(D = \mathbb{R}\) B. \(D = \left( {1; + \infty } \right)\) C. \(D = \mathbb{R}\backslash \left\{ 1 \right\}\) D. \(D = \left[ {1; + \infty } \right)\) Câu 3: Cho hàm số\(y = {\mkern 1mu} \left\{ {\begin{array}{*{20}{l}}{\frac{2}{{x - 1}},{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x \in \left( { - \infty ;{\mkern 1mu} {\mkern 1mu} 0} \right)}\\{\sqrt {x + 1} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x \in \left[ {0;{\mkern 1mu} {\mkern 1mu} 2} \right]}\\{{x^2} - 1,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x \in \left( {2;{\mkern 1mu} {\mkern 1mu} 5} \right]}\end{array}} \right..{\mkern 1mu} {\mkern 1mu} \) Tính \(f(4),\) ta được kết quả: A. 2/3 B. 15 C. D. kết quả khác Câu 4: Cho hàm số \(y = a{x^2} + bx + c{\mkern 1mu} {\mkern 1mu} \left( {a < 0} \right)\) có đồ thị (P). Khẳng định nào sau đây là khẳng định đúng? A. Hàm số đồng biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\) B. Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\) C. Đồ thị luôn cắt trục hoành tại 2 điểm phân biệt D. Đồ thị có trục đối xứng là đường thẳng \(x = {\rm{ \;}} - \frac{b}{{2a}}\) Câu 5: Cho hàm số \(y = \left( {m - 4} \right){x^2} - 3x + 2\). Hàm số đã cho là hàm số bậc hai khi: A. m = 4 B. m > 4 C. m < 4 D. \(m \ne 4\) Câu 6: Cho tam thức bậc hai \(f(x) = a{x^2} + bx + c{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (a \ne 0)\). Điều kiện cần và đủ để \(f(x) \le 0,\forall x \in \mathbb{R}\) là: A. \(\left\{ {\begin{array}{*{20}{l}}{a < 0}\\{\Delta {\rm{ \;}} > 0}\end{array}} \right.\) B. \(\left\{ {\begin{array}{*{20}{l}}{a < 0}\\{\Delta {\rm{ \;}} > 0}\end{array}} \right.\) C. \(\left\{ {\begin{array}{*{20}{l}}{a > 0}\\{\Delta {\rm{ \;}} \ge 0}\end{array}} \right.\) D. \(\left\{ {\begin{array}{*{20}{l}}{a < 0}\\{\Delta {\rm{ \;}} \le 0}\end{array}} \right.\) Câu 7: Mệnh đề nào sau đây đúng? A. Có duy nhất một vectơ cùng phương với mọi vectơ. B. Có ít nhất hai vectơ có cùng phương với mọi vectơ. C. Có vô số vectơ cùng phương với mọi vectơ. D. Không có vectơ nào cùng phương với mọi vectơ. Câu 8: Cho hình bình hành ABCD, giao điểm của hai đường chéo là \(O\). Tìm mệnh đề sai trong các mệnh đề sau: A. \(\overrightarrow {CO} {\rm{ \;}} - \overrightarrow {OB} {\rm{ \;}} = \overrightarrow {BA} \) B. \(\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {DB} \) C. \(\overrightarrow {DA} {\rm{ \;}} - \overrightarrow {DB} {\rm{ \;}} = \overrightarrow {OD} {\rm{ \;}} - \overrightarrow {OC} \) D. \(\overrightarrow {DA} {\rm{ \;}} + \overrightarrow {DB} {\rm{ \;}} + \overrightarrow {DC} {\rm{ \;}} = \vec 0\) Câu 9: Cho ba điểm A,B,C phân biệt. Đẳng thức nào sau đây là đẳng thức sai? A. \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {AC} \) B. \(\overrightarrow {CA} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {BC} \) C. \(\overrightarrow {BA} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} = \overrightarrow {BC} \) D. \(\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {AC} {\rm{ \;}} = \overrightarrow {CB} \) Câu 10: Cho hình bình hành ABCD tâm \(O\). Đẳng thức nào sau đây sai? A. \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BD} } \right|\) B. \(\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {DA} } \right|\) C. \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\) D. \(\left| {\overrightarrow {AO} } \right| = \frac{1}{2}\left| {\overrightarrow {CA} } \right|\) Câu 11: Cho \(\vec a\) và \(\vec b\) là hai vecto cùng hướng và đều khác vecto \(\vec 0\). Mệnh đề nào sau đây đúng? A. \(\vec a \cdot \vec b = \left| {\vec a} \right|{\mkern 1mu} \cdot \left| {\vec b} \right|\) B. \(\vec a \cdot \vec b = 0\) C. \(\vec a \cdot \vec b = {\rm{\;}} - 1\) D. \(\vec a \cdot \vec b = {\rm{\;}} - \left| {\vec a} \right|{\mkern 1mu} \cdot \left| {\vec b} \right|\) Câu 12: Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị như hình dưới đây. Mệnh đề nào sau đây đúng?
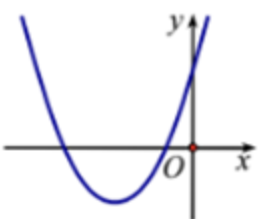
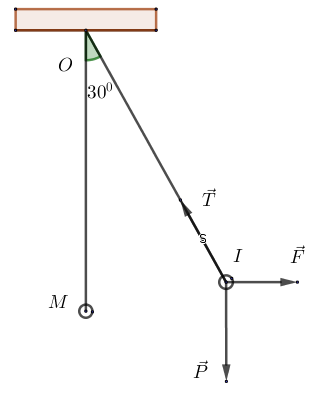
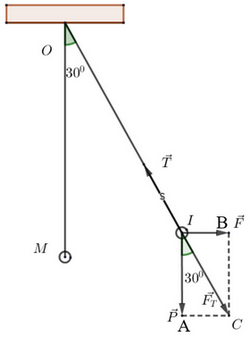
A. a > 0, b = 0, c > 0 B. a > 0, b < 0, c > 0 C. a > 0, b > 0, c > 0 D. a < 0, b > 0, c > 0 Câu 13: Cho hàm số \(f\left( x \right) = {x^2} - 4x + 5\) khẳng định nào sau đây đúng? A. Hàm số đồng biến trên \(\left( { - \infty ;2} \right)\), nghịch biến trên \(\left( {2; + \infty } \right)\). B. Hàm số đồng biến trên các khoảng\(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\). C. Hàm số nghịch biến trên các khoảng\(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\). D. Hàm số nghịch biến trên \(\left( { - \infty ;2} \right)\), đồng biến trên \(\left( {2; + \infty } \right)\). Câu 14: Tập xác định của hàm số \(y = \sqrt {5 - 4x - {x^2}} \) là A. \(\left[ { - 5;1} \right]\) B. \(\left[ { - \frac{1}{5};1} \right]\) C. \(\left( { - \infty ; - 5} \right] \cup \left[ {1; + \infty } \right)\) D. \(\left( { - \infty ; - \frac{1}{5}} \right] \cup \left[ {1; + \infty } \right)\) Câu 15: Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình \(\sqrt {2{x^2} - 2} {\rm{\;}} = x + 1\). Khi đó \({x_1} + {x_2}\) bằng A. \(0\). B. \(2\). C. \(1\). D. \( - 1\). Câu 16: Cho tam giác ABC đều cạnh \(a\). Gọi \(M\) là trung điểm BC. Khẳng định nào sau đây đúng? A. \(\overrightarrow {MB} {\rm{ \;}} = \overrightarrow {MC} \) B. \(\overrightarrow {AM} {\rm{ \;}} = \frac{{a\sqrt 3 }}{2}\) C. \(\overrightarrow {AM} {\rm{ \;}} = a\) D. \(\left| {\overrightarrow {AM} } \right| = \frac{{a\sqrt 3 }}{2}\) Câu 17: Cho tam giác ABC và điểm \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} {\rm{ \;}} - \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\). Mệnh đề nào sau đây sai? A. MABC là hình bình hành. B. \(\overrightarrow {AM} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {AC} \) C. \(\overrightarrow {BA} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {BM} \) D. \(\overrightarrow {MA} {\rm{ \;}} = \overrightarrow {BC} \) Câu 18: Cho hình vuông ABCD có cạnh bằng \(a\). Khi đó \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right|\) bằng: A. \(\frac{{a\sqrt 5 }}{2}\) B. \(\frac{{a\sqrt 3 }}{2}\) C. \(\frac{{a\sqrt 3 }}{3}\) D. \(a\sqrt 5 \) Câu 19: Cho tam giác ABC. Trên cạnh BC lấy điểm \(D\) sao cho \(\overrightarrow {BD} {\rm{\;}} = \frac{1}{3}\overrightarrow {BC} \). Khi đó, vectơ \(\overrightarrow {AD} \) bằng A. \(\frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \) B. \(\frac{1}{3}\overrightarrow {AB} {\rm{\;}} + \frac{2}{3}\overrightarrow {AC} \) C. \(\overrightarrow {AB} {\rm{\;}} + \frac{2}{3}\overrightarrow {AC} \) D. \(\frac{5}{3}\overrightarrow {AB} {\rm{\;}} - \frac{1}{3}\overrightarrow {AC} \) Câu 20: Cho tam giác ABC có \(AB = 2,\)\(BC = 4,{\mkern 1mu} {\mkern 1mu} CA = 3\). Tính \(\overrightarrow {AB} .\overrightarrow {AC} \) và \(\cos A\). A. \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{\;}} = \frac{3}{2}\) và \(\cos A = \frac{1}{4}\) B. \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{\;}} = {\rm{\;}} - \frac{3}{2}\) và \(\cos A = {\rm{\;}} - \frac{1}{4}\) C. \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{\;}} = {\rm{\;}} - \frac{2}{3}\) và \(\cos A = {\rm{\;}} - \frac{1}{4}\) D. \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{\;}} = \frac{2}{3}\) và \(\cos A = \frac{1}{4}\) Câu 21: Cho hàm số bậc hai \(y = a{x^2} + bx + 3{\mkern 1mu} {\mkern 1mu} \left( {a \ne 0} \right)\) có đồ thị (P), biết rằng đồ thị (P) có đỉnh S(-2;-1). Tính 2a – b? A. -2 B. -1 C. 1 D. 2 Câu 22: Với giá trị nào của \(b\) thì tam thức bậc hai \(f\left( x \right) = {x^2} - bx + 3\) có nghiệm? A. \(b \in \left[ { - {\mkern 1mu} 2\sqrt 3 ;{\mkern 1mu} {\mkern 1mu} 2\sqrt 3 } \right]\) B. \(b \in \left( { - {\mkern 1mu} 2\sqrt 3 ;{\mkern 1mu} {\mkern 1mu} 2\sqrt 3 } \right)\) C. \(b \in \left( { - {\mkern 1mu} \infty ;{\mkern 1mu} {\mkern 1mu} - {\mkern 1mu} 2\sqrt 3 } \right] \cup \left[ {2\sqrt 3 ;{\mkern 1mu} {\mkern 1mu} + {\mkern 1mu} \infty } \right)\) D. \(b \in \left( { - {\mkern 1mu} \infty ;{\mkern 1mu} {\mkern 1mu} - {\mkern 1mu} 2\sqrt 3 } \right) \cup \left( {2\sqrt 3 ;{\mkern 1mu} {\mkern 1mu} + {\mkern 1mu} \infty } \right)\) Câu 23: Tổng tất cả các giá trị nguyên của \(x\) để tam thức \(f\left( x \right) = 2{x^2} - 7x - 9\) nhận giá trị âm là A. \(7\) B. \(8\) C. \(9\) D. 10 Câu 24: Số nghiệm của phương trình \(\sqrt {5x - 1} = \sqrt {3x - 2} + \sqrt {x - 1} \) là A. 3 B. 2 C. 1 D. 0 Câu 25: Cho tứ giác ABCD. Gọi \(M,N,P,Q\) lần lượt là trung điểm của AB, BC, CD, DA. Khẳng định nào sau đây là sai? A. \(\overrightarrow {MN} {\rm{ \;}} = \overrightarrow {QP} \) B. \(\left| {\overrightarrow {QP} } \right| = \left| {\overrightarrow {MN} } \right|\) C. \(\overrightarrow {MQ} {\rm{ \;}} = \overrightarrow {NP} \) D. \(\left| {\overrightarrow {MN} } \right| = \left| {\overrightarrow {AC} } \right|\) Câu 26: Cho tứ giác ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tìm giá trị của \(k\) thích hợp điển vào đẳng thức vec tơ\(\overrightarrow {MN} {\rm{ \;}} = k\left( {\overrightarrow {AD} {\rm{ \;}} + \overrightarrow {BC} } \right)\). A. \(k = 3\) B. \(k = \frac{1}{2}\) C. \(k = 2.\) D. \(k = \frac{1}{3}\) Câu 27: Tam giác ABC có \(AB = AC = a\), \(\angle BAC = {120^0}\). Độ dài vectơ \(\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} \) là A. \(a\sqrt 3 \) B. \(a\) C. \(a\sqrt 2 \) D. \(\frac{{a\sqrt 3 }}{2}\) Câu 28: Cho tam giác ABC có \(BC = a,\)\(CA = b,{\mkern 1mu} {\mkern 1mu} AB = c\). Gọi \(M\) là trung điểm của cạnh BC. Tính \(\overrightarrow {AM} .\overrightarrow {BC} \). A. \(\overrightarrow {AM} .\overrightarrow {BC} {\rm{\;}} = \frac{{{b^2} - {c^2}}}{2}\) B. \(\overrightarrow {AM} .\overrightarrow {BC} {\rm{\;}} = \frac{{{c^2} + {b^2}}}{2}\) C. \(\overrightarrow {AM} .\overrightarrow {BC} {\rm{\;}} = \frac{{{c^2} + {b^2} + {a^2}}}{3}\) D. \(\overrightarrow {AM} .\overrightarrow {BC} {\rm{\;}} = \frac{{{c^2} + {b^2} - {a^2}}}{2}\) Câu 29: Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 4x + 3 > 0}\\{3{x^2} - 10x + 3 \le 0}\\{4{x^2} - x - 3 > 0}\end{array}} \right.\) có nghiệm là: A. Vô nghiệm B. \( - \frac{3}{4} < x < \frac{1}{3}\) C. \(\frac{1}{3} < x < 1\) D. \(1 < x < 3\) Câu 30: Một con lắc đơn đang đứng yên tại vị trí cân bằng \(M\). Thực tập viên tác dụng một lực \(\vec F\) lên con lắc đưa nó đến vị trí \(I\) và giữ yên như hình vẽ.
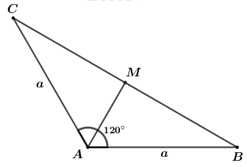
Biết rằng con lắc đang chịu tác động của lực căng dây \(\vec T\) có cường độ 30N, trọng lực \(\vec P\) và lực tác dụng \(\vec F\). Hãy xác định cường độ của lực \(\vec F\)? A. \(30\sqrt 3 {\mkern 1mu} \left( N \right)\) B. \(30{\mkern 1mu} \left( N \right)\) C. \(15{\mkern 1mu} \left( N \right)\) D. \(15\sqrt 2 {\mkern 1mu} \left( N \right)\) II. Phần tự luận Câu 1: Cho \(\Delta ABC,\) \(I\) là trung điểm BC và \(D,{\mkern 1mu} {\mkern 1mu} E\) thỏa mãn\(\;\overrightarrow {BD} {\rm{\;}} = \overrightarrow {DE} {\rm{\;}} = \overrightarrow {EC} \) a) Chứng minh rằng: \(\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = \overrightarrow {AD} {\rm{\;}} + \overrightarrow {AE} \) b) Tính: \(\overrightarrow {AS} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \overrightarrow {AD} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} + \overrightarrow {AE} \) theo \(\overrightarrow {AI} .\) Từ đó suy ra \(A,{\mkern 1mu} {\mkern 1mu} S,{\mkern 1mu} {\mkern 1mu} I\) thẳng hàng. Câu 2: Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe honda Future Fi với chi phí mua vào một chiếc là 27 triệu và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bản mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất. Câu 3: Tìm giá trị nhỏ nhất của a để phương trình \({x^2} - 6ax + 9{a^2} - 2a + 2 = 0\) có hai nghiệm lớn hơn 3. ----- HẾT ----- Lời giải HƯỚNG DẪN GIẢI CHI TIẾT I. Phần trắc nghiệm
Câu 1 (NB): Phương pháp: Thay tọa độ từng điểm vào hệ bất phương trình. Cách giải: Ta có \(\left\{ {\begin{array}{*{20}{l}}{3x - 4y + 12 \ge 0}\\{x + y - 5 \ge 0}\\{x + 1 > 0}\end{array}} \right.\), kiểm tra đáp án thấy \(N\left( {4{\mkern 1mu} ;{\mkern 1mu} 3} \right)\) thoả mãn. Chọn B. Câu 2 (NB): Phương pháp: Hàm phân thức xác định khi mẫu thức khác 0. Cách giải: ĐKXĐ: \(2x - 2 \ne 0 \Leftrightarrow x \ne 1\). Vậy TXĐ của hàm số là \(D = \mathbb{R}\backslash \left\{ 1 \right\}\). Chọn C. Câu 3 (NB): Cách giải: \(f(4) = {4^2} - 1 = {\rm{\;}}15\) Chọn B. Câu 4 (NB): Phương pháp: Đồ thị hàm số \(y = a{x^2} + bx + c\) có trục đối xứng là đường thẳng \(x = {\rm{ \;}} - \frac{b}{{2a}}\). Với a < 0: Hàm số đồng biến trên \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\) và nghịch biến trên \(\left( { - \frac{b}{{2a}}; + \infty } \right)\). Cách giải: Vì a < 0 nên hàm số đồng biến trên \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\) và nghịch biến trên \(\left( { - \frac{b}{{2a}}; + \infty } \right)\). Do đó A và B sai. Đồ thị có trục đối xứng là đường thẳng \(x = {\rm{ \;}} - \frac{b}{{2a}}\) nên D đúng. Chưa đủ dữ kiện để xác định số giao điểm của đồ thị hàm số với trục hoành nên C sai. Chọn D. Câu 5 (NB): Phương pháp: Hàm số bậc hai có dạng \(y = a{x^2} + bx + c{\mkern 1mu} {\mkern 1mu} \left( {a \ne 0} \right)\). Cách giải: Hàm số \(y = \left( {m - 4} \right){x^2} - 3x + 2\) là hàm số bậc hai khi \(m - 4 \ne 0 \Leftrightarrow m \ne 4\). Chọn D. Câu 6 (NB): Phương pháp: Áp dụng quy tắc dấu của tam thức bậc hai. Cách giải: \(f(x) = a{x^2} + bx + c{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (a \ne 0)\), \(f(x) \le 0,\forall x \in \mathbb{R}\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a < 0}\\{\Delta {\rm{ \;}} \le 0}\end{array}} \right.\). Chọn D. Câu 7 (NB): Phương pháp: Vectơ-không cùng phương với mọi vectơ. Cách giải: Vectơ-không cùng phương với mọi vectơ. Chọn A. Câu 8 (NB): Phương pháp: Xét từng đáp án. Sử dụng công thức hình bình hành, các tính chất của phép cộng vectơ Cách giải: Ta có: \(\overrightarrow {DA} {\rm{ \;}} + \overrightarrow {DB} {\rm{ \;}} + \overrightarrow {DC} {\rm{ \;}} = \left( {\overrightarrow {DA} {\rm{ \;}} + \overrightarrow {DC} } \right) + \overrightarrow {DB} {\rm{ \;}} = \overrightarrow {DB} {\rm{ \;}} + \overrightarrow {DB} {\rm{ \;}} = 2\overrightarrow {DB} {\rm{ \;}} \ne \vec 0\). Chọn D. Câu 9 (NB): Phương pháp: Sử dụng quy tắc cộng vectơ. Cách giải: Với ba điểm A,B,C phân biệt ta có: \(\overrightarrow {CA} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {CB} \). Vậy đáp án B sai Chọn B. Câu 10 (NB): Phương pháp: Áp dụng tính chất của hình bình hành. Cách giải:
Vì ABCD là hình bình hành nên \(AB = DC,{\mkern 1mu} {\mkern 1mu} AD = BC,{\mkern 1mu} {\mkern 1mu} AO = \frac{1}{2}AC\). Do vậy các đáp án đúng là: \(\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {DA} } \right|\), \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\), \(\left| {\overrightarrow {AO} } \right| = \frac{1}{2}\left| {\overrightarrow {CA} } \right|\) \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BD} } \right|\) là đáp án sai vì AC và BD là hai đường chéo của hình bình hành ABCD nên \(AC \ne BD\). Chọn A. Câu 11 (NB): Phương pháp: Áp dụng công thức: \(\vec a.\vec b = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec b} \right)\) Hai vecto cùng hướng thì góc giữa hai vecto bằng \({0^0}\). Cách giải: Ta có: \(\vec a \cdot \vec b = \)\(\left| {\vec a} \right|{\mkern 1mu} \cdot \left| {\vec b} \right| \cdot \cos \left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec b} \right)\) Do \(\vec a\) và \(\vec b\) là hai vecto cùng hướng nên \(\left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec b} \right) = {0^^\circ }\)\( \Rightarrow \cos \left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec b} \right) = 1\). \( \Rightarrow \vec a \cdot \vec b = \left| {\vec a} \right|{\mkern 1mu} \cdot \left| {\vec b} \right|\) Vậy \(\vec a \cdot \vec b = \left| {\vec a} \right|{\mkern 1mu} \cdot \left| {\vec b} \right|\). Chọn A. Câu 12 (TH): Phương pháp: Hàm số bậc hai \(y = a{x^2} + bx + c\) với a > 0 có bề lõm hướng lên và với a < 0 có bề lõm hướng xuống. Giao với trục tung tại điểm nằm trên trục hoành thì c > 0 và nằm dưới trục hoành thì c < 0. Đồ thị cắt trục hoành tại 2 điểm có hoành độ âm nên phương trình \(a{x^2} + bx + c = 0\) có 2 nghiệm âm. Cách giải: Đồ thị hàm số có bề lõm hướng lên nên a > 0 => Loại D. Đồ thị cắt trục tung tại điểm nằm trên trục hoành nên c > 0. Đồ thị cắt trục hoành tại 2 điểm có hoành độ âm nên phương trình \(a{x^2} + bx + c = 0\) có 2 nghiệm âm. \( \Rightarrow \frac{{ - b}}{a} < 0 \Leftrightarrow {\rm{ \;}} - b < 0 \Leftrightarrow b > 0\) => Loại A và B. Chọn C. Câu 13 (TH): Phương pháp: Với \(a > 0\), hàm số bậc hai đồng biến trên \(\left( {\frac{{ - b}}{{2a}}; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;\frac{{ - b}}{{2a}}} \right)\) Cách giải: Đồ thị hàm số \(f\left( x \right) = {x^2} - 4x + 5\) có \({x_I} = \frac{{ - b}}{{2a}} = 2\) và có \(a = 1 > 0\) Suy ra hàm số nghịch biến trên \(\left( { - \infty ;2} \right)\), đồng biến trên \(\left( {2; + \infty } \right)\). Chọn D. Câu 14 (TH): Phương pháp: Hàm số \(y = \sqrt {f(x)} \) xác định khi \(f\left( x \right) \ge 0.\) Xét dấu hàm số \(f\left( x \right) = 5 - 4x - {x^2}\), để giải \(f\left( x \right) \ge 0.\) Cách giải: Hàm số xác định khi \(5{x^2} - 4x - 1 \ge 0\). Ta có \(a = {\rm{ \;}} - 1 < 0;\Delta {\rm{ \;}} > 0.\) \(f\left( x \right)\) có hai nghiệm phân biệt \(x = 1;x = {\rm{ \;}} - 5.\) Vậy \( - 5 \le x \le 1\). Chọn A. Câu 15 (TH): Phương pháp: Giải phương trình \(\sqrt A {\rm{\;}} = B \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{B \ge 0}\\{A = {B^2}}\end{array}} \right.\) Cách giải: \(\sqrt {2{x^2} - 2} = x + 1 \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\2{x^2} - 2 = {\left( {x + 1} \right)^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\2{x^2} - 2 = {x^2} + 2x + 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\{x^2} - 2x - 3 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\\left[ \begin{array}{l}x = 3\\x = - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 1\end{array} \right.\) Khi đó \({x_1} + {x_2} = 3 + \left( { - 1} \right) = 2\). Chọn B. Câu 16 (TH): Phương pháp: - Kiểm tra đáp án A bằng cách xác định hướng và độ dài của hai vecto \(\overrightarrow {MB} ;{\mkern 1mu} {\mkern 1mu} \overrightarrow {MC} .\) - Kiểm tra các đáp án B, C, D bằng cách tính độ dài đoạn thẳng AM. Cách giải: Tam giác đều ABC cạnh a, có độ dài đường trung tuyến AM là: \(A{M^2} = \frac{{A{C^2} + A{B^2}}}{2} - \frac{{B{C^2}}}{4} = \frac{{{a^2} + {a^2}}}{2} - \frac{{{a^2}}}{4} = \frac{{3a}}{4}.\) \( \Rightarrow AM = \frac{{\sqrt 3 a}}{2}\)\( \Rightarrow \overrightarrow {\left| {AM} \right|} {\rm{ \;}} = \frac{{\sqrt 3 a}}{2}.\) Chọn D. Câu 17 (TH): Phương pháp: Biến đổi \(\overrightarrow {MA} {\rm{ \;}} - \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\) về hai vectơ bằng nhau. Xác định vị trí điểm M dựa vào điều kiện vừa tìm được. Cách giải:
Ta có \(\overrightarrow {MA} {\rm{ \;}} - \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\)\( \Leftrightarrow \overrightarrow {BA} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Leftrightarrow \overrightarrow {MC} {\rm{ \;}} = \overrightarrow {AB} \) \( \Rightarrow \) MABC là hình bình hành. Chọn A. Câu 18 (TH): Phương pháp: Gọi M là trung điểm BC. Sử dụng tính chất trung điểm. Cách giải:
Gọi \(M\) là trung điểm BC. Ta có: \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2AM = 2\sqrt {A{B^2} + B{M^2}} {\rm{ \;}} = 2\sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} {\rm{ \;}} = a\sqrt 5 \). Chọn D. Câu 19 (TH): Phương pháp: Áp dụng định nghĩa tích của vecto với một số, quy tắc cộng vecto để phân tích vecto. Cách giải:
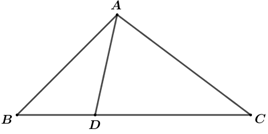
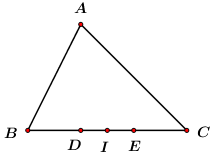
Ta có: \(\overrightarrow {AD} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \overrightarrow {BD} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {BC} \) \({\mkern 1mu} = \overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\left( {\overrightarrow {BA} {\rm{\;}} + \overrightarrow {AC} } \right)\)\( = \overrightarrow {AB} {\rm{\;}} - \frac{1}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \)\({\mkern 1mu} {\mkern 1mu} = \frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \) \( \Rightarrow \overrightarrow {AD} {\rm{\;}} = \frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \) Chọn A. Câu 20 (TH): Phương pháp: Áp dụng: + \({\left( {\overrightarrow {AB} {\rm{\;}} - \overrightarrow {AC} } \right)^2} = A{B^2} + A{C^2} - 2\overrightarrow {AB} .\overrightarrow {AC} \) và quy tắc cộng vecto. + \(\cos A = \cos \left( {\overrightarrow {AB} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}}\) Cách giải: Tam giác ABC:\(AB = 2,\)\(BC = 4,{\mkern 1mu} {\mkern 1mu} CA = 3\). Ta có: \({\left( {\overrightarrow {AB} {\rm{\;}} - \overrightarrow {AC} } \right)^2} = A{B^2} + A{C^2} - 2\overrightarrow {AB} .\overrightarrow {AC} \) \( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} \)\( = \frac{{{{\overrightarrow {AB} }^2} + {{\overrightarrow {AC} }^2} - {{\left( {\overrightarrow {AB} {\rm{\;}} - \overrightarrow {AC} } \right)}^2}}}{2}\)\( = \frac{{{{\overrightarrow {AB} }^2} + {{\overrightarrow {AC} }^2} - {{\overrightarrow {BC} }^2}}}{2}\)\( = \frac{{A{B^2} + A{C^2} - B{C^2}}}{2}\)\( = \frac{{{2^2} + {3^2} - {4^2}}}{2} = \frac{{ - 3}}{2}\) Lại có: \(\cos A = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}}\)\( = \frac{{ - \frac{3}{2}}}{{2.3}} = \frac{{ - 1}}{4}\) Chọn B. Câu 21 (VD): Phương pháp: Từ tọa độ đỉnh suy ra 2 phương trình, giải hệ tìm a, b. Cách giải: Vì S(-2;-1) là đỉnh của (P) nên \(\left\{ {\begin{array}{*{20}{l}}{\frac{{ - b}}{{2a}} = {\rm{ \;}} - 2}\\{ - 1 = 4a - 2b + 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4a - b = 0}\\{4a - 2b = {\rm{ \;}} - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 4}\end{array}} \right.\). Vậy 2a – b = 2.1 – 4 = -2. Chọn A. Câu 22 (VD): Phương pháp: \(f\left( x \right) = 0\) có nghiệm\( \Leftrightarrow \Delta {\rm{ \;}} \ge 0\) Cách giải: Xét \(f\left( x \right) = 0 \Leftrightarrow {x^2} - bx + 3 = 0\) \(\left( 1 \right)\) Để tam thức bậc hai \(f\left( x \right)\) có nghiệm thì \(\left( 1 \right)\)có nghiệm \( \Leftrightarrow \Delta {\rm{ \;}} \ge 0\)\( \Leftrightarrow {b^2} - 12 \ge 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{b \ge 2\sqrt 3 }\\{b \le {\rm{ \;}} - 2\sqrt 3 }\end{array}} \right.\). \( \Rightarrow b \in \left( { - {\mkern 1mu} \infty ;{\mkern 1mu} {\mkern 1mu} - {\mkern 1mu} 2\sqrt 3 } \right] \cup \left[ {2\sqrt 3 ;{\mkern 1mu} {\mkern 1mu} + {\mkern 1mu} \infty } \right)\) Chọn C. Câu 23 (VD): Phương pháp: Tìm các nghiệm của \(f\left( x \right)\), lập bảng xét dấu và kết luận. Cách giải: Giải: \(f\left( x \right) = 0 \Leftrightarrow 2{x^2} - 7x - 9 = 0\)\( \Leftrightarrow \left( {2x - 9} \right)\left( {x + 1} \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = {\rm{ \;}} - 1}\\{x = \frac{9}{2}}\end{array}} \right.\) Dựa vào bảng xét dấu ta có: \(f\left( x \right) = 2{x^2} - 7x - 9 < 0\)\( \Leftrightarrow {\rm{ \;}} - 1 < x < \frac{9}{2}\) Mà \(x \in \mathbb{Z} \Rightarrow x \in \left\{ {0;{\mkern 1mu} {\mkern 1mu} 1;{\mkern 1mu} {\mkern 1mu} 2;{\mkern 1mu} {\mkern 1mu} 3;{\mkern 1mu} {\mkern 1mu} 4} \right\}\) Tổng tất cả các số nguyên \(x\) thỏa mãn là: \(0 + {\mkern 1mu} 1 + 2 + 3 + 4 = 10\) Chọn D. Câu 24 (VD): Phương pháp: Bước 1: Tìm tập xác định (\(\sqrt A \) xác định khi và chỉ khi \(A \ge 0\)) Bước 2: Giải phương trình bằng phương pháp bình phương 2 vế. Cách giải: \(\sqrt {5x - 1} {\rm{\;}} = \sqrt {3x - 2} {\rm{\;}} + \sqrt {x - 1} \) TXĐ: \(D = \left[ {1; + \infty } \right]\) \(\begin{array}{l}\sqrt {5x - 1} = \sqrt {3x - 2} + \sqrt {x - 1} \\ \Leftrightarrow {\left( {\sqrt {5x - 1} } \right)^2} = {\left( {\sqrt {3x - 2} + \sqrt {x - 1} } \right)^2}\\ \Leftrightarrow 5x - 1 = 3x - 2 + x - 1 + 2\sqrt {\left( {3x - 2} \right)\left( {x - 1} \right)} \\ \Leftrightarrow x + 2 = 2\sqrt {3{x^2} - 5x + 2} \end{array}\) \( \Leftrightarrow \left\{ \begin{array}{l}x + 2 \ge 0\\{\left( {x + 2} \right)^2} = 4\left( {3{x^2} - 5x + 2} \right)\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\{x^2} + 4x + 4 = 12{x^2} - 20x + 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\11{x^2} - 24x + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\\left[ \begin{array}{l}x = 2\\x = \frac{2}{{11}}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {Tm} \right)\\x = \frac{2}{{11}}\,\left( {ktm} \right)\end{array} \right.\) Vậy phương trình có 1 nghiệm \(x = 2\) Chọn C. Câu 25 (VD): Phương pháp: - Vẽ hình, xác định các vectơ liên quan. - Hình MNPQ là hình gì? - Dựa vào tính chất hình MNPQ và MN là đường trung bình của tam ABC để chọn đáp án đúng. Cách giải:
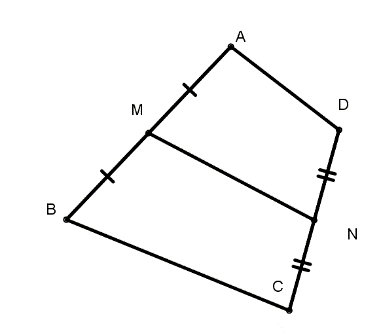
Ta có \(\left\{ {\begin{array}{*{20}{l}}{MN\parallel PQ}\\{MN = PQ}\end{array}} \right.\) (do cùng song song và bằng \(\frac{1}{2}AC\)). Do đó MNPQ là hình bình hành. Suy ra \(\overrightarrow {MN} {\rm{ \;}} = \overrightarrow {QP} \); \(\left| {\overrightarrow {QP} } \right| = \left| {\overrightarrow {MN} } \right|\); \(\overrightarrow {MQ} {\rm{ \;}} = \overrightarrow {NP} \). Ta có: MN là đường trung bình tam giác ABC Suy ra \(MN = \frac{1}{2}AC \Rightarrow \overrightarrow {MN} {\rm{ \;}} = \frac{1}{2}\overrightarrow {AC} \) Chọn D. Câu 26 (VD): Phương pháp: Biểu diễn \(\overrightarrow {MN} \) qua các vectơ \(\overrightarrow {MA} ,{\mkern 1mu} \overrightarrow {AD} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {DN} \). Biểu diễn \(\overrightarrow {MN} \) qua các vectơ \(\overrightarrow {MB} ,{\mkern 1mu} \overrightarrow {BC} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {CN} \). Cộng hai biểu thức trên và biểu diễn \(\overrightarrow {MN} \) qua \(\overrightarrow {AD} ,\overrightarrow {BC} .\) Cách giải: Ta có: \(\overrightarrow {MN} {\rm{ \;}} = \overrightarrow {MA} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} + \overrightarrow {DN} \) (1) \(\overrightarrow {MN} {\rm{ \;}} = \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} + \overrightarrow {CN} \) (2) Cộng vế với vế của (1) và (2) ta được \(2\overrightarrow {MN} {\rm{ \;}} = \overrightarrow {AD} {\rm{ \;}} + \overrightarrow {BC} \) \( \Rightarrow \overrightarrow {MN} {\rm{ \;}} = \frac{1}{2}\left( {\overrightarrow {AD} {\rm{ \;}} + \overrightarrow {BC} } \right) \Rightarrow k = \frac{1}{2}\). Chọn B. Câu 27 (VD): Phương pháp: Áp dụng quy tắc cộng vecto, quy tắc hình bình hành để tìm vecto tổng. Tính độ dài vecto vừa tìm được. Cách giải:
Ta có: \(\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = 2\overrightarrow {AM} \) \(\left| {\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2\left| {\overrightarrow {AM} } \right| = 2.a.\cos {60^0} = a\) Chọn B. Câu 28 (VD): Phương pháp: Nếu \(M\) là trung điểm của cạnh BC thì \(\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = 2\overrightarrow {AM} \). Cách giải:
Vì \(M\) là trung điểm của BC nên \(\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = 2\overrightarrow {AM} \)\( \Rightarrow \overrightarrow {AM} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} } \right)\) Ta có: \(\overrightarrow {AM} .\overrightarrow {BC} \)\( = \frac{1}{2}\left( {\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} } \right).\overrightarrow {BC} \)\( = \frac{1}{2}\left( {\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} } \right).\left( {\overrightarrow {AC} {\rm{\;}} - \overrightarrow {AB} } \right)\) \( = \frac{1}{2}\left( {{{\overrightarrow {AC} }^2} - {{\overrightarrow {AB} }^2}} \right)\)\( = \frac{1}{2}\left( {A{C^2} - A{B^2}} \right)\)\( = \frac{{{b^2} - {c^2}}}{2}\) Vậy \(\overrightarrow {AM} .\overrightarrow {BC} {\rm{\;}} = \frac{{{b^2} - {c^2}}}{2}\). Chọn A. Câu 29 (VDC): Phương pháp: Giải từng bất phương trình sau đó lấy giao các tập hợp nghiệm. Cách giải: \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 4x + 3 > 0}\\{3{x^2} - 10x + 3 \le 0}\\{4{x^2} - x - 3 > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x < 1 \vee x > 3}\\{\frac{1}{3} \le x \le 3}\\{x < {\rm{\;}} - \frac{3}{4} \vee x > 1}\end{array}} \right. \Leftrightarrow x \in \emptyset \) Chọn A. Câu 30 (VDC): Phương pháp: Giả sử \(\vec P{\rm{ \;}} = \overrightarrow {IA} \); \(\vec F{\rm{ \;}} = \overrightarrow {IB} \) có hợp lực \(\overrightarrow {{F_T}} {\rm{ \;}} = \overrightarrow {IC} \), lực căng dây \(\vec T{\rm{ \;}} = \overrightarrow {IN} \). Đặt \(x > 0\) là cường độ lực \(\vec F\), \(x > 0\), đơn vị: \(N\). Tính góc \(\angle ICB\), \(\angle CIA\). Tính IC dựa và tam giác IAC vuông tại A. Vì con lắc đứng yên nên \(IC = \left| {\overrightarrow {IC} } \right| = \left| {\vec T} \right|\). Từ đó tìm x. Cách giải: Giả sử \(\vec P{\rm{ \;}} = \overrightarrow {IA} \); \(\vec F{\rm{ \;}} = \overrightarrow {IB} \) có hợp lực \(\overrightarrow {{F_T}} {\rm{ \;}} = \overrightarrow {IC} \), lực căng dây \(\vec T{\rm{ \;}} = \overrightarrow {IN} \). Đặt \(x,x > 0\) là cường độ của lực \(\vec F\), đơn vị \(N\).
Dễ thấy \(\widehat {IOM} = \widehat {ICB}\) (so le trong) suy ra \(\widehat {ICB} = {30^^\circ }\). Mà \(\widehat {ICB} = \widehat {CIA}\) nên \(\widehat {CIA} = {30^^\circ }\). Ta có \(AC = IB = x \Rightarrow IC = \frac{{AC}}{{{\rm{sin3}}{0^^\circ }}} = 2x\). Do con lắc đứng yên tại \(I\)nên lực căng dây \(\vec T\) có cùng cường độ với hợp lực \(\overrightarrow {{F_T}} \). Nên \(2x = 30 \Leftrightarrow x = 15\). Vậy cường độ của lực tác dụng \(\vec F\) bằng 15N. Chọn C. II. Phần tự luận Câu 1 (TH): Phương pháp: a) Cho \(I\) là trung điểm của AB ta có: \(\overrightarrow {IA} {\rm{\;}} + \overrightarrow {IB} {\rm{\;}} = \vec 0.\) b) Biểu diễn \(\overrightarrow {AS} \) theo vecto \(\overrightarrow {AI} \) rồi suy ra \(A,{\mkern 1mu} {\mkern 1mu} S,{\mkern 1mu} {\mkern 1mu} I\) thẳng hàng. Cách giải:
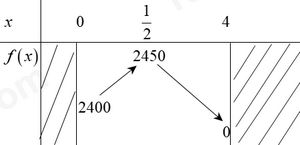
a) Chứng minh rằng: \(\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = \overrightarrow {AD} {\rm{\;}} + \overrightarrow {AE} \) Ta có: \(\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = 2\overrightarrow {AI} \) (I là trung điểm của BC) Vì \(BD = DE = EC,{\mkern 1mu} {\mkern 1mu} I\) là trung điểm BC \( \Rightarrow I\) là trung điểm DE \(\begin{array}{*{20}{l}}{ \Rightarrow \overrightarrow {AD} {\rm{\;}} + \overrightarrow {AE} {\rm{\;}} = 2\overrightarrow {AI} }\\{ \Rightarrow \overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = \overrightarrow {AD} {\rm{\;}} + \overrightarrow {AE} \;\left( { = 2\overrightarrow {AI} } \right)}\end{array}\) b) Tính: \(\overrightarrow {AS} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \overrightarrow {AD} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} + \overrightarrow {AE} \) theo \(\overrightarrow {AI} .\) Từ đó suy ra \(A,{\mkern 1mu} {\mkern 1mu} S,{\mkern 1mu} {\mkern 1mu} I\) thẳng hàng. \(\overrightarrow {AS} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \overrightarrow {AD} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} + \overrightarrow {AE} \) \(\begin{array}{*{20}{l}}{ \Rightarrow \overrightarrow {AS} {\rm{\;}} = \left( {\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} } \right) + \left( {\overrightarrow {AD} {\rm{\;}} + \overrightarrow {AE} } \right)}\\{ \Rightarrow \overrightarrow {AS} {\rm{\;}} = 2\overrightarrow {AI} {\rm{\;}} + 2\overrightarrow {AI} }\\{ \Rightarrow \overrightarrow {AS} {\rm{\;}} = 4\overrightarrow {AI} }\end{array}\) \( \Rightarrow \) \(A,{\mkern 1mu} {\mkern 1mu} S,{\mkern 1mu} {\mkern 1mu} I\) thẳng hàng. Câu 2 (VD): Phương pháp: - Gọi x đồng là số tiền mà doanh nghiệp A dự định giảm giá; \(0 \le x \le 4\). - Lập phương trình tính lợi nhuận khi bán một chiếc xe. - Tính số xe mà doanh nghiệp bán được trong một năm. - Lập hàm số biểu thị lợi nhuận doanh nghiệp thu được trong một năm. - Xét sự biến thiên hàm số trên \([0;4]\) và tìm giá trị lớn nhất của nó. - Kết luận bài toán. Cách giải: Gọi x đồng là số tiền mà doanh nghiệp A dự định giảm giá; \(0 \le x \le 4\). Khi đó: Lợi nhuận thu được khi bán một chiếc xe là \(31 - x - 27 = 4 - x\) (đồng). Số xe mà doanh nghiệp sẽ bán được trong một năm là: \(600 + 200x\) (chiếc). Lợi nhuận mà doanh nghiệp thu được trong một năm là: \(f\left( x \right) = \left( {4 - x} \right)\left( {600 + 200x} \right) = {\rm{ \;}} - 200{x^2} + 200x + 2400.\) Xét hàm số \(f\left( x \right) = {\rm{ \;}} - 200{x^2} + 200x + 2400\) trên đoạn \([0;4]\) có bảng biến thiên sau:
Suy ra \(\mathop {\max }\limits_{[0;4]} f\left( x \right) = 2450 \Leftrightarrow x = \frac{1}{2}.\) Vậy giá mới của chiếc xe là 30,5 triệu đồng thì lợi nhuận thu được là cao nhất. Câu 3 (VDC): Phương pháp: Điều kiện tương đương là: \(\left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{x_1} + {x_2} > 6}\\{\left( {{x_1} - 3} \right)\left( {{x_2} - 3} \right) > 0}\end{array}} \right.\) Giải điều kiện dựa vào định lí Vi-ét. Cách giải: Phương trình có 2 nghiệm phân biệt \({x_1} > {x_2} > 3\). Điều kiện để phương trình có hai nghiệm lớn hơn 3 là: \(\left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{x_1} + {x_2} > 6}\\{\left( {{x_1} - 3} \right)\left( {{x_2} - 3} \right) > 0}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2a - 2 > 0}\\{6a > 6}\\{{x_1}{x_2} - 3\left( {{x_1} + {x_2}} \right) + 9 > 0}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 1}\\{9{a^2} - 2a + 2 - 3.6a + 9 > 0}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 1}\\{9{a^2} - 20a + 11 > 0}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 1}\\{\left[ {\begin{array}{*{20}{l}}{a > \frac{{11}}{9}}\\{a < 1}\end{array}} \right.}\end{array}} \right. \Leftrightarrow a > \frac{{11}}{9}\). Do a nguyên và nhỏ nhất nên a = 2.
|