Đề khảo sát chất lượng đầu năm Toán 10 Cánh diều - Đề số 2Đề bài
Câu 1 :
Cho đường thẳng \(d\):\(y = - kx + b\,\,\left( {k \ne 0} \right)\). Hệ số góc của đường thẳng \(d\) là
Câu 2 :
Cho hàm số \(y = \left( {1 - \sqrt {m - 1} } \right){x^2}.\) Hàm số đã cho đồng biến khi \(x < 0\) nếu:
Câu 3 :
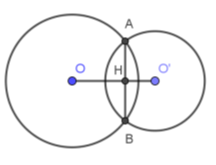
Cho hai đường tròn \(\left( {O;6\,cm} \right)\) và \(\left( {O';2\,cm} \right)\) cắt nhau tại \(A,B\) sao cho \(OA\) là tiếp tuyến của \(\left( {O'} \right)\). Độ dài dây \(AB\) là
Câu 4 :
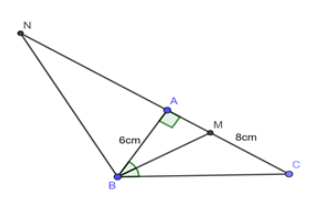
Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AB = 6cm\) và \(AC = 8cm\) . Các phân giác trong và ngoài của góc \(B\) cắt đường thẳng \(AC\) lần lượt tại \(M\) và \(N\). Tính các đoạn thẳng \(AM\) và \(AN\).
Câu 5 :
Cho hình trụ có bán kính đáy \(R = 12\,cm\) và diện tích toàn phần \(672\pi \)\(c{m^2}\) . Tính chiều cao của hình trụ.
Câu 6 :
Giải hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{1}{{x - 2}} + \dfrac{4}{{3y + 1}} = 5\\\dfrac{2}{{x - 2}} - \dfrac{4}{{3y + 1}} = - 2\end{array} \right.\)
Câu 7 :
Rút gọn biểu thức \(\sqrt {9{{\left( { - a} \right)}^2}.{{\left( {3 - 4a} \right)}^6}} \) với \(a \ge \dfrac{3}{4}\) ta được:
Câu 8 :
Cho \(x,y\) là các số tự nhiên thỏa mãn điều kiện \(\left( {x + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 2.\) Tính giá trị của biểu thức \(Q = x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} .\)
Câu 9 :
Cho hình cầu có bán kính \(5\,cm\). Một hình nón cũng có bán kính đáy bằng \(5\,cm\) và có diện tích toàn phần bằng diện tích mặt cầu. Tính chiều cao của hình nón. 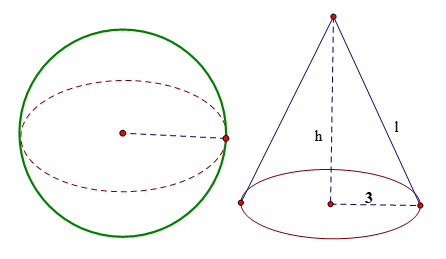
Câu 10 :
Cho hai đường tròn \(\left( {O;4cm} \right)\) và \(\left( {O';3cm} \right)\) biết \(OO' = 5cm\). Hai đường tròn trên cắt nhau tại \(A\) và \(B\). Độ dài \(AB\) là:
Câu 11 :
Cho tam giác \(ABC\) có các đường cao \(BD,CE\) . Chọn khẳng định đúng.
Câu 12 :
Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x - 3\) và \(\left( {{d_2}} \right):y = - \dfrac{1}{2}x + 2\) Tìm \(m\) để ba đường thẳng \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy.
Câu 13 :
Cho hình nón có chiều cao \(h = 24cm\) và thể tích \(V = 800\pi \,\left( {c{m^3}} \right)\) . Tính diện tích toàn phần của hình nón.
Câu 14 :
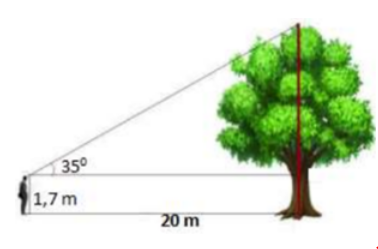
Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất)
Câu 15 :
Cho tam giác \(MNP\) có \(MN = 5cm,NP = 12cm,MP = 13cm\). Vẽ đường tròn \(\left( {M;NM} \right)\). Khẳng định nào sau đây là đúng?
Câu 16 :
Cho (P): \(y = {x^2}\) và đường thẳng \(d':y = 2x + 1\). Phương trình đường thẳng d // d’ và d tiếp xúc (P) là:
Câu 17 :
Cho phương trình \(a{x^2} + bx + c = 0\,\,(a \ne 0)\) có biệt thức \(b = 2b';\Delta ' = b{'^2} - ac\). Phương trình đã cho vô nghiệm khi
Câu 18 :
Rút gọn rồi tính giá trị của biểu thức \(Q = \dfrac{{2x - 3\sqrt x - 2}}{{\sqrt x - 2}}\) tại \(x = 2020 - 2\sqrt {2019} \)
Câu 19 :
Không dùng bảng số và máy tính, hãy so sánh \(\cot 50^\circ \) và \(\cot 46^\circ \)
Câu 20 :
Một người đi xe máy từ A đến B với vận tốc trung bình 30km/giờ. Khi đi được 1 giờ thì xe bị hỏng, người đó phải dừng lại để sửa xe mất 10 phút. Sau khi sửa xong người đó đi tiếp tới B, để đến B đúng giờ đã định người đó phải tăng vận tốc thêm 6km/h. Tính độ dài quãng đường AB.
Câu 21 :
Hai số \(u = m;v = 1 - m\) là nghiệm của phương trình nào dưới đây?
Câu 22 :
Kết quả phân tích đa thức \({x^2} + xy-x-y\;\) thành nhân tử là:
Câu 23 :
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 1\,cm,\,\,BC = 2\,cm.\) Tính các tỉ số lượng giác \(\sin B;\cos B\)
Câu 24 :
Cho \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo tỉ số \(\dfrac{3}{5}\) và chu vi của \(\Delta A'B'C'\) là $60cm.$ Khi đó chu vi \(\Delta ABC\) là:
Câu 25 :
Chọn khẳng định đúng. Nếu phương trình \(a{x^2} = mx + n\) có hai nghiệm phân biệt thì đường thẳng \(d:y = mx + n\) và parabol \(\left( P \right):y = a{x^2}\)
Câu 26 :
Nếu \(\Delta ABC\) vuông tại A có \(BH = 9,HC = 25\) thì đường cao \(AH\) có độ dài là: 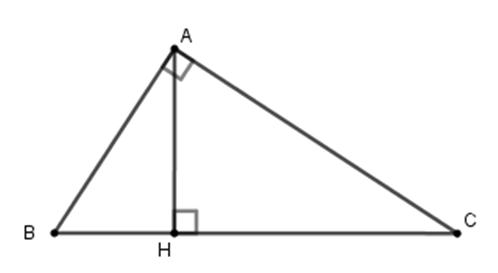
Câu 27 :
Đưa thừa số \(5x\sqrt {\dfrac{{ - 12}}{{{x^3}}}} \) (\(x < 0\)) vào trong dấu căn ta được:
Câu 28 :
Giải phương trình \(\dfrac{{x - 1}}{{x + 2}} - \dfrac{{1 - x}}{{2 - x}} = \dfrac{{2({x^2} + 2)}}{{{x^2} - 4}}\) ta được tập nghiệm là:
Câu 29 :
Thu gọn $\sqrt[3]{{ - \dfrac{1}{{27{a^3}}}}}$ với $a \ne 0$ ta được
Câu 30 :
Không tính cụ thể, bất đẳng thức nào sau đây là bất đẳng thức sai?
Câu 31 :
Giá trị của biểu thức \(\sqrt {17 - 12\sqrt 2 } + \sqrt {9 + 4\sqrt 2 } \).
Câu 32 :
Tìm hệ số góc của đường thẳng \(d\) biết \(d\) đi qua điểm \(M\left( { - 3;2} \right)\) và \(N\left( {1; - 1} \right)\).
Câu 33 :
“Trong các dây của một đường tròn, đường kính là dây có độ dài…”. Cụm từ thích hợp điền vào chỗ trống là:
Câu 34 :
Hình lập phương có thể tích \(512c{m^3}\) thì có diện tích toàn phần là:
Câu 35 :
Giá trị của biểu thức \(2\sqrt {32} - \sqrt {27} - 4\sqrt 8 + 3\sqrt {75} \) là:
Câu 36 :
Cho phương trình \({x^2} - 2\left( {m - 1} \right)x + 2{m^2} - 3m + 1 = 0\), với \(m\) là tham số. Gọi \({x_1},{x_2}\) là nghiệm của phương trình. Chọn câu đúng.
Câu 37 :
Hình vẽ bên là đồ thị của hàm số nào dưới đây? 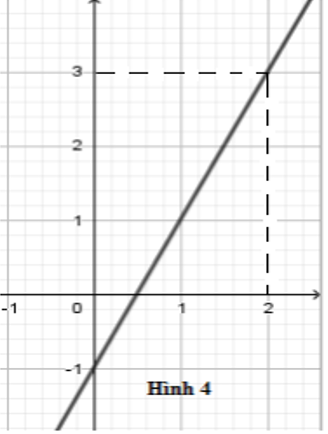
Câu 38 :
Trong các hàm số \(y = - 3x + 2;y = - \dfrac{1}{3}\left( { - x + 1} \right);y = 6 - \dfrac{x}{2};y = - \left( {1 - 2x} \right)\), có bao nhiêu hàm số nghịch biến?
Câu 39 :
Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy \(S = 36\pi \,c{m^2}\) và chiều cao \(h = 8\,cm\) . Nếu trục lăn đủ \(10\) vòng thì diện tích tạo trên sân phẳng là bao nhiêu? 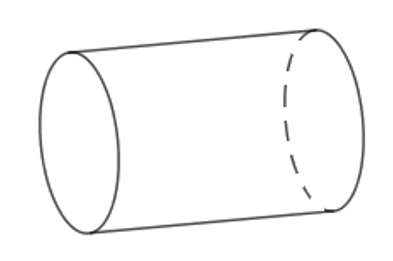
Câu 40 :
Tìm giá trị nhỏ nhất của biểu thức \(A = \sqrt {{m^2} + 2m + 1} + \sqrt {{m^2} - 8m + 16} \).
Lời giải và đáp án
Câu 1 :
Cho đường thẳng \(d\):\(y = - kx + b\,\,\left( {k \ne 0} \right)\). Hệ số góc của đường thẳng \(d\) là
Đáp án : A Lời giải chi tiết :
Đường thẳng \(d\) có phương trình \(y = - kx + b\,\,\left( {k \ne 0} \right)\) có \( - k\) là hệ số góc.
Câu 2 :
Cho hàm số \(y = \left( {1 - \sqrt {m - 1} } \right){x^2}.\) Hàm số đã cho đồng biến khi \(x < 0\) nếu:
Đáp án : C Phương pháp giải :
Dựa vào tính chất của đồ thị hàm số bậc \(2:y = a{x^2}\left( {a \ne 0} \right)\): Khi \(a > 0\) thì bề lõm quay lên trên (tức là hàm số đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0\)). Khi \(a < 0\) thì bề lõm quay xuống dưới (tức là hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\)) Lời giải chi tiết :
Hàm số đồng biến khi \(x < 0\) thì \(1 - \sqrt {m - 1} < 0 \Rightarrow m > 2\)
Câu 3 :
Cho hai đường tròn \(\left( {O;6\,cm} \right)\) và \(\left( {O';2\,cm} \right)\) cắt nhau tại \(A,B\) sao cho \(OA\) là tiếp tuyến của \(\left( {O'} \right)\). Độ dài dây \(AB\) là
Đáp án : B Phương pháp giải :
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và hệ thức lượng trong tam giác vuông. Lời giải chi tiết :
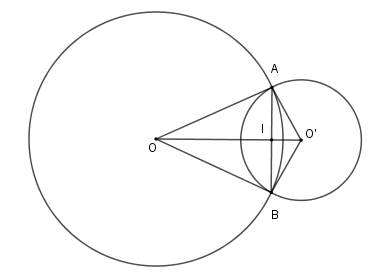 Vì \(OA\) là tiếp tuyến của \(\left( {O'} \right)\) nên \(\Delta OAO'\) vuông tại \(A\). Vì \(\left( O \right)\) và \(\left( {O'} \right)\) cắt nhau tại \(A,B\) nên đường nối tâm \(OO'\) là trung trực của đoạn \(AB\). Gọi giao điểm của \(AB\) và \(OO'\) là \(I\) thì \(AB \bot OO'\) tại \(I\) là trung điểm của \(AB\) Áp dụng hệ thức lượng trong tam giác vuông \(OAO'\) ta có \(\dfrac{1}{{A{I^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O'{A^2}}} = \dfrac{1}{{{6^2}}} + \dfrac{1}{{{2^2}}} \Rightarrow AI = \dfrac{{3\sqrt {10} }}{5}\,cm \Rightarrow AB = \dfrac{{6\sqrt {10} }}{5}\,cm\)
Câu 4 :
Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AB = 6cm\) và \(AC = 8cm\) . Các phân giác trong và ngoài của góc \(B\) cắt đường thẳng \(AC\) lần lượt tại \(M\) và \(N\). Tính các đoạn thẳng \(AM\) và \(AN\).
Đáp án : D Phương pháp giải :
Sử dụng định lý Pitago cho tam giác ABC vuông tại A để tính độ dài cạnh BC. Theo đề bài ta có AM, AN lần lượt là các đường phân giác trong và ngoài của góc B. Khi đó áp dụng tính chất tia phân giác của một góc ta có: \(\dfrac{{AM}}{{MC}} = \dfrac{{AN}}{{NC}} = \dfrac{{AB}}{{BC}}.\) Lời giải chi tiết :
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {6^2} + {8^2} = 100 \Rightarrow BC = 10\left( {cm} \right)\) Vì \(BM\) là tia phân giác trong của góc \(B \Rightarrow \dfrac{{MA}}{{MC}} = \dfrac{{AB}}{{BC}}\) (Tính chất đường phân giác) \( \Rightarrow \dfrac{{MA}}{{MC + MA}} = \dfrac{{AB}}{{BC + AB}} \Rightarrow \dfrac{{MA}}{{AC}} = \dfrac{{AB}}{{BC + AB}}\)\( \Rightarrow \dfrac{{MA}}{8} = \dfrac{6}{{10 + 6}} \Rightarrow MA = 3cm\) Vì \(BM;BN\) là tia phân giác trong và ngoài của góc \(B \Rightarrow \angle NBM = {90^0}\) Áp dụng hệ thức lượng trong \(\Delta ABM\) vuông tại \(B\) có đường cao \(BA\) ta có: \( \Rightarrow A{B^2} = AM.AN\)\( \Leftrightarrow {6^2} = 3.AN \Leftrightarrow AN = 12\left( {cm} \right)\)
Câu 5 :
Cho hình trụ có bán kính đáy \(R = 12\,cm\) và diện tích toàn phần \(672\pi \)\(c{m^2}\) . Tính chiều cao của hình trụ.
Đáp án : A Phương pháp giải :
Sử dụng công thức tính diện tích toàn phần của hình trụ để tính chiều cao hình trụ \(S_{tp}=S_{xq}+S_{2\,đáy}=2\pi.R.h+2 \pi R^2\) Lời giải chi tiết :
Diện tích toàn phần của hình trụ là: \(24\pi h + 2\pi {.12^2} = 672\pi \) Suy ra \(h = 16\,(cm)\)
Câu 6 :
Giải hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{1}{{x - 2}} + \dfrac{4}{{3y + 1}} = 5\\\dfrac{2}{{x - 2}} - \dfrac{4}{{3y + 1}} = - 2\end{array} \right.\)
Đáp án : A Phương pháp giải :
Tìm điều kiện xác định của hệ phương trình. Đặt \(\left\{ \begin{array}{l}u = \dfrac{1}{{x - 2}}\\v = \dfrac{1}{{3y + 1}}\end{array} \right.\). Giải hệ phương trình được \(u,v \Rightarrow x,y\) đối chiếu điều kiện và kết luận. Lời giải chi tiết :
Điều kiện: \(x \ne 2,\,\,\,y \ne - \dfrac{1}{3}.\) Đặt \(\left\{ \begin{array}{l}u = \dfrac{1}{{x - 2}}\\v = \dfrac{1}{{3y + 1}}\end{array} \right..\) Khi đó ta có hệ phương trình \( \Leftrightarrow \left\{ \begin{array}{l}u + 4v = 5\\2u - 4v = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3u = 3\\u + 4v = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}u = 1\\v = 1\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}\dfrac{1}{{x - 2}} = 1\\\dfrac{1}{{3y + 1}} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 2 = 1\\3y + 1 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\,\,\,\,\left( {tm} \right)\\y = 0\,\,\,\left( {tm} \right)\end{array} \right.\) Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {3;0} \right).\)
Câu 7 :
Rút gọn biểu thức \(\sqrt {9{{\left( { - a} \right)}^2}.{{\left( {3 - 4a} \right)}^6}} \) với \(a \ge \dfrac{3}{4}\) ta được:
Đáp án : A Phương pháp giải :
- Sử dụng công thức khai phương một tích: Với hai số \(a,b\) không âm, ta có \(\sqrt a .\sqrt b = \sqrt {ab} \) - Sử dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\) Lời giải chi tiết :
\(\sqrt {9{{\left( { - a} \right)}^2}.{{\left( {3 - 4a} \right)}^6}} = \sqrt 9 \sqrt {{{\left( { - a} \right)}^2}} .\sqrt {{{\left( {3 - 4a} \right)}^6}} = \sqrt {{3^2}} \sqrt {{{\left( { - a} \right)}^2}} .\sqrt {{{\left( {{{\left( {3 - 4a} \right)}^3}} \right)}^2}} = \left| 3 \right|\left| { - a} \right|.\left| {{{\left( {3 - 4a} \right)}^3}} \right| = 3a.{\left( {4a - 3} \right)^3}\) (vì \(a \ge \dfrac{3}{4} \Rightarrow 3 - 4a \le 0 \Rightarrow \left| {3 - 4a} \right| = 4a - 3 \Rightarrow \left| {{{\left( {3 - 4a} \right)}^3}} \right| = {\left( {4a - 3} \right)^3}\))
Câu 8 :
Cho \(x,y\) là các số tự nhiên thỏa mãn điều kiện \(\left( {x + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 2.\) Tính giá trị của biểu thức \(Q = x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} .\)
Đáp án : D Phương pháp giải :
Biến đổi biểu thức đã cho bằng phương pháp nhân liên hợp sau đó tính giá trị biểu thức \(Q\). Lời giải chi tiết :
Theo đề bài ta có: \(\left( {x + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 2\) \(\begin{array}{l} \Rightarrow \left( {x + \sqrt {{x^2} + 1} } \right)\left( {\sqrt {{x^2} + 1} - x} \right)\left( {y + \sqrt {{y^2} + 1} } \right)\left( {\sqrt {{y^2} + 1} - y} \right) = 2\left( {\sqrt {{x^2} + 1} - x} \right)\left( {\sqrt {{y^2} + 1} - y} \right)\\ \Leftrightarrow \left( {{x^2} + 1 - {x^2}} \right)\left( {{y^2} + 1 - {y^2}} \right) = 2\left( {\sqrt {{x^2} + 1} - x} \right)\left( {\sqrt {{y^2} + 1} - y} \right)\\ \Leftrightarrow 1 = 2\left[ {\left( {\sqrt {{x^2} + 1} \sqrt {{y^2} + 1} + xy} \right) - \left( {x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} } \right)} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\end{array}\) Lại có: \(\left( {x + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 2\) \(\begin{array}{l} \Rightarrow \left( {\sqrt {{x^2} + 1} \sqrt {{y^2} + 1} + xy} \right) + \left( {x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} } \right) = 2\,\,\\ \Leftrightarrow 2\left( {\sqrt {{x^2} + 1} \sqrt {{y^2} + 1} + xy} \right) + 2\left( {x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} } \right) = 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array}\) Từ \(\left( 1 \right),\left( 2 \right)\) ta được: \( - 4\left( {x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} } \right) = - 3\)\( \Rightarrow x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} = \dfrac{3}{4}.\) Vậy \(Q = \dfrac{3}{4}.\)
Câu 9 :
Cho hình cầu có bán kính \(5\,cm\). Một hình nón cũng có bán kính đáy bằng \(5\,cm\) và có diện tích toàn phần bằng diện tích mặt cầu. Tính chiều cao của hình nón. 
Đáp án : C Phương pháp giải :
Sử dụng công thức diện tích mặt cầu \(S = 4\pi {R^2}\) và diện tích toàn phần của hình nón \({S_{tp}} = \pi Rl + \pi {R^2}\) Sử dụng công thức liên hệ \({l^2} = {R^2} + {h^2}\) để tính chiều cao của hình nón. Lời giải chi tiết :
Gọi \(l\) là độ dài đường sinh của hình nón. Vì bán kính hình cầu và bán kính đáy của hình nón bằng nhau nên từ giả thiết ta có: \(4\pi {R^2} = \pi Rl + \pi {R^2}\) \(4{R^2} = Rl + {R^2} \) \(3{R^2} = Rl \) \(l = 3R = 3.5 = 15\,(cm)\) Sử dụng công thức tính chiều cao hình nón ta có: \({h^2} = {l^2} - {R^2} = {15^2} - {5^2} = 200\) Suy ra \(h = 10\sqrt 2 \,\,(cm)\)
Câu 10 :
Cho hai đường tròn \(\left( {O;4cm} \right)\) và \(\left( {O';3cm} \right)\) biết \(OO' = 5cm\). Hai đường tròn trên cắt nhau tại \(A\) và \(B\). Độ dài \(AB\) là:
Đáp án : B Phương pháp giải :
Dựa vào tính chất hai đường tròn cắt nhau. Định lí Pi-ta-go đảo. Hệ thức lượng trong tam giác vuông. Lời giải chi tiết :
Xét tam giác \(OAO'\) có \(O{A^2} + O'{A^2} = OO{'^2}\) (vì \({4^2} + {3^2} = {5^2}\)) nên tam giác \(OAO'\) vuông tại \(A\). Xét tam giác \(OAO'\) có \(AH\) là đường cao nên \(AH.OO' = OA.O'A \Rightarrow AH = \dfrac{{OA.O'A}}{{OO'}} = \dfrac{{4.3}}{5} = \dfrac{{12}}{5}\) Mà \(AB = 2AH\) nên \(AB = \dfrac{{24}}{5} = 4,8cm\)
Câu 11 :
Cho tam giác \(ABC\) có các đường cao \(BD,CE\) . Chọn khẳng định đúng.
Đáp án : A Phương pháp giải :
Sử dụng: Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp. Lời giải chi tiết :
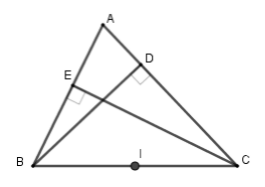 Gọi \(I\) là trung điểm của \(BC\). Xét tam giác \(BEC\) vuông tại \(E\) có \(EI = IB = IC = \dfrac{{BC}}{2}\) (vì \(EI\) là đường trung tuyến ứng với cạnh huyền) Xét tam giác \(BDC\) vuông tại \(D\) có \(DI = IB = IC = \dfrac{{BC}}{2}\) (vì \(DI\) là đường trung tuyến ứng với cạnh huyền) Từ đó ta có \(ID = IE = IB = IC = \dfrac{{BC}}{2}\) nên bốn điểm \(B,E,D,C\) cùng nằm trên một đường tròn có bán kính \(R = \dfrac{{BC}}{2}\). Ta thấy \(IA > ID\) nên điểm \(A\) không thuộc đường tròn trên.
Câu 12 :
Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x - 3\) và \(\left( {{d_2}} \right):y = - \dfrac{1}{2}x + 2\) Tìm \(m\) để ba đường thẳng \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy.
Đáp án : A Phương pháp giải :
Xét phương trình hoành độ giao điểm của hai đồ thị \((d_1);(d_2)\) để tìm \(x,\) thay giá trị \(x\) vừa tìm được vào 1 trong hai phương trình để tìm \(y.\) Ba đường thẳng đồng quy khi và chỉ khi đường thẳng thứ ba đi qua giao điểm của hai đường thẳng còn lại. Lời giải chi tiết :
Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\): \(2x - 3 = - \dfrac{1}{2}x + 2 \Leftrightarrow 2x + \dfrac{1}{2}x = 2 + 3 \Leftrightarrow \dfrac{5}{2}x = 5 \Leftrightarrow x = 2\) Thay \(x = 2\) vào hàm số \(y = 2x - 3\) ta được \(y = 2.2 - 3 = 1.\) Vậy tọa độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(A\left( {2;1} \right)\). Ba đường thẳng \(\left( {{d_1}} \right)\) , \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy \( \Rightarrow \left( {{d_3}} \right)\) đi qua giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)\( \Rightarrow A \in \left( {{d_3}} \right)\) Thay tọa độ điểm \(A\) vào hàm số \(\left( {{d_3}} \right):\,\,y = 3x - 2m - 3\) ta được: \(1 = 3.2 - 2m - 3\)\( \Rightarrow 2m = 6 - 3 - 1 \Rightarrow m = 1\) Vậy \(m = 1\) thì ba đường thẳng \(\left( {{d_1}} \right)\) , \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy.
Câu 13 :
Cho hình nón có chiều cao \(h = 24cm\) và thể tích \(V = 800\pi \,\left( {c{m^3}} \right)\) . Tính diện tích toàn phần của hình nón.
Đáp án : D Phương pháp giải :
Sử dụng công thức thể tich khối nón \(V = \dfrac{1}{3}\pi {R^2}h\) để tính bán kính đường tròn đáy Sử dụng công thức liên hệ \({R^2} + {h^2} = {l^2}\) để tìm đường sinh của hình nón Sử dụng công thức tính diện tích toàn phần của hình nón \({S_{tp}} = \pi Rl + \pi {R^2}\) Lời giải chi tiết :
Ta có \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {R^2}.24 = 800\pi \) suy ra \( {R^2} = 100 \) do đó \( R = 10\,cm\) Và \({R^2} + {h^2} = {l^2} \) hay \( {10^2} + {24^2} = {l^2} \) suy ra \( l = 26\,cm\) Diện tích toàn phần của hình nón là: \({S_{tp}} = \pi Rl + \pi {R^2} = \pi .10.26 + \pi {.10^2} = 360\pi \,\left( {c{m^2}} \right)\)
Câu 14 :
Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất)
Đáp án : B Phương pháp giải :
Sử dụng giá trị lượng giác của một góc nhọn trong tam giác vuông để giải tam giác. Trong tam giác vuông, độ dài 1 cạnh góc vuông bằng cạnh góc vuông còn lại nhân tang góc đối. Lời giải chi tiết :
Chiều cao của cây là : \(h = 1,7 + 20.\tan 35^\circ \approx 15,7m\).
Câu 15 :
Cho tam giác \(MNP\) có \(MN = 5cm,NP = 12cm,MP = 13cm\). Vẽ đường tròn \(\left( {M;NM} \right)\). Khẳng định nào sau đây là đúng?
Đáp án : A Phương pháp giải :
Sử dụng cách chứng minh tiếp tuyến Để chứng minh đường thẳng \(d\) là tiếp tuyến của đường tròn \(\left( {O;R} \right)\) tại tiếp điểm là \(M\) ta chứng minh \(OM \bot d\) tại \(M\) và \(M \in \left( O \right)\). Lời giải chi tiết :
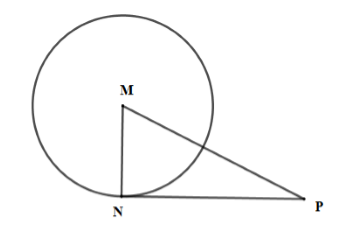 +) Xét tam giác \(MNP\) có \(M{P^2} = {13^2} = 169;N{M^2} + N{P^2} = {5^2} + {12^2} = 169\)\( \Rightarrow M{P^2} = N{M^2} + N{P^2}\) \( \Rightarrow \Delta MNP\) vuông tại N (định lý Pytago đảo) \( \Rightarrow MN \bot NP\) mà \(N \in \left( {M;MN} \right)\) nên \(NP\) là tiếp tuyến của \(\left( {M;MN} \right)\)
Câu 16 :
Cho (P): \(y = {x^2}\) và đường thẳng \(d':y = 2x + 1\). Phương trình đường thẳng d // d’ và d tiếp xúc (P) là:
Đáp án : A Phương pháp giải :
- \(d//d' \Leftrightarrow \left\{ \begin{array}{l} - d tiếp xúc (P) khi và chỉ khi phương trình hoành độ giao điểm của d và (P) có nghiệm kép. Lời giải chi tiết :
Gọi d: y = ax + b \(d//d':y = 2x + 1 \Rightarrow \left\{ \matrix{a = 2 \hfill \cr b \ne 1 \hfill \cr} \right.\) d : 2x + b tiếp xúc với (P) suy ra phương trình \({x^2} = 2x + b\) có nghiệm kép \( \Leftrightarrow {x^2} - 2x - b = 0\) có nghiệm kép \( \Leftrightarrow \Delta ' = 0 \Leftrightarrow 1 + b = 0 \Leftrightarrow b = - 1\) Vậy \(d:y = 2x - 1.\)
Câu 17 :
Cho phương trình \(a{x^2} + bx + c = 0\,\,(a \ne 0)\) có biệt thức \(b = 2b';\Delta ' = b{'^2} - ac\). Phương trình đã cho vô nghiệm khi
Đáp án : D Phương pháp giải :
Dựa vào công thức nghiệm thu gọn của phương trình bậc hai một ẩn: Xét phương trình bậc hai một ẩn $a{{x}^{2}}+bx+c=0\left( a\ne 0 \right)$, với $b=2b'$ và $\Delta '=b{{'}^{2}}-ac$. - Nếu $\Delta '>0$ thì phương trình có hai nghiệm phân biệt: ${{x}_{1}}=\frac{-b'+\sqrt{\Delta '}}{a};{{x}_{2}}=\frac{-b'-\sqrt{\Delta '}}{a}$. - Nếu $\Delta '=0$ thì phương trình có nghiệm kép ${{x}_{1}}={{x}_{2}}=-\frac{b'}{a}$. - Nếu $\Delta '<0$ thì phương trình vô nghiệm. Lời giải chi tiết :
Phương trình vô nghiệm khi $\Delta '<0$.
Câu 18 :
Rút gọn rồi tính giá trị của biểu thức \(Q = \dfrac{{2x - 3\sqrt x - 2}}{{\sqrt x - 2}}\) tại \(x = 2020 - 2\sqrt {2019} \)
Đáp án : A Phương pháp giải :
Tìm ĐKXĐ của biểu thức, rút gọn biểu thức Q sau đó xét xem \(x = 2020 - 2\sqrt {2019} \) có thỏa mãn điều kiện bài toán hay không rồi thay vào biểu thức và tính giá trị biểu thức Q. Lời giải chi tiết :
ĐKXĐ: \(x \ge 0,\,\,x \ne 4.\) \(Q = \dfrac{{2x - 3\sqrt x - 2}}{{\sqrt x - 2}}\)\( = \dfrac{{\left( {2\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}{{\sqrt x - 2}}\)\( = 2\sqrt x + 1.\) Ta có: \(x = 2020 - 2\sqrt {2019} \)\( = 2019 - 2\sqrt {2019} + 1\)\( = {\left( {\sqrt {2019} - 1} \right)^2}\,\,\,\left( {tm} \right)\) \( \Rightarrow \sqrt x = \sqrt {{{\left( {\sqrt {2019} - 1} \right)}^2}} = \left| {\sqrt {2019} - 1} \right| = \sqrt {2019} - 1\,.\) Thay \(\sqrt x = \sqrt {2019} - 1\) vào biểu thức \(Q\) ta được: \(Q = 2\left( {\sqrt {2019} - 1} \right) + 1\)\( = 2\sqrt {2019} - 2 + 1\)\( = 2\sqrt {2019} - 1.\) Vậy \(x = 2020 - 2\sqrt {2019} \) thì \(Q = 2\sqrt {2019} - 1.\)
Câu 19 :
Không dùng bảng số và máy tính, hãy so sánh \(\cot 50^\circ \) và \(\cot 46^\circ \)
Đáp án : B Phương pháp giải :
Sử dụng nhận xét : Với góc nhọn \(\alpha ,\,\beta ,\) ta có: \(\alpha < \beta \Leftrightarrow \cot \alpha > \cot \beta \) Lời giải chi tiết :
Vì \(46^\circ < 50^\circ \Leftrightarrow \cot 46^\circ > \cot 50^\circ \).
Câu 20 :
Một người đi xe máy từ A đến B với vận tốc trung bình 30km/giờ. Khi đi được 1 giờ thì xe bị hỏng, người đó phải dừng lại để sửa xe mất 10 phút. Sau khi sửa xong người đó đi tiếp tới B, để đến B đúng giờ đã định người đó phải tăng vận tốc thêm 6km/h. Tính độ dài quãng đường AB.
Đáp án : A Phương pháp giải :
Giải theo các bước sau: + Lập phương trình: Chọn ẩn và đặt điều kiện; biểu diễn đại lượng chưa biết theo ẩn và đại lượng đã biết; lập phương trình biểu thị mối quan hệ giữa các đại lượng + Giải phương trình + Đối chiếu điều kiện rồi kết luận Lời giải chi tiết :
Đổi 10 phút = \(\dfrac{1}{6}\) giờ. Gọi quãng đường AB dài là \(x\left( {km} \right)\left( {x > 30{\rm{ }}} \right)\). Suy ra quãng đường từ khi dừng lại sửa xe đến B là \(x- 30{\rm{ }}\left( {km} \right)\). Thời gian dự định đi từ A đến B là \(\dfrac{x}{{30}}\)(h). Thời gian thực tế đi từ A đến B là \(1 + \dfrac{1}{6} + \dfrac{{x - 30}}{{36}}\) (h). Ta có phương trình: \(1 + \dfrac{1}{6} + \dfrac{{x - 30}}{{36}} = \dfrac{x}{{30}}\) \( \Leftrightarrow \dfrac{{36 + 6 + x - 30}}{{36}} = \dfrac{x}{{30}}\) \(\begin{array}{l} \Leftrightarrow \dfrac{{12 + x}}{{36}} = \dfrac{x}{{30}}\\ \Rightarrow 30\left( {12 + x} \right) = 36.x\\ \Leftrightarrow 360 + 30x = 36x\\ \Leftrightarrow 6x = 360\\ \Leftrightarrow x = 60\left( {tm} \right)\end{array}\) Vậy quãng đường \(AB\) dài \(60\) km.
Câu 21 :
Hai số \(u = m;v = 1 - m\) là nghiệm của phương trình nào dưới đây?
Đáp án : A Phương pháp giải :
Hai số \(u,v\) có \(u + v = S;uv = P\) thì \(u,v\) là hai nghiệm của phương trình \({x^2} - Sx + P = 0\). Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}S = u + v = m + 1 - m = 1\\P = uv = m\left( {1 - m} \right)\end{array} \right.\) Suy ra \(u,v\) là hai nghiệm của phương trình \({x^2} - Sx + P = 0\) hay \({x^2} - x + m\left( {1 - m} \right) = 0\).
Câu 22 :
Kết quả phân tích đa thức \({x^2} + xy-x-y\;\) thành nhân tử là:
Đáp án : A Phương pháp giải :
Sử dụng phương pháp nhóm hạng tử để phân tích đa thức thành nhân tử. Lời giải chi tiết :
\({x^2} + xy - x - y = x\left( {x + y} \right) - \left( {x + y} \right)\)\( = \left( {x - 1} \right)\left( {x + y} \right)\).
Câu 23 :
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 1\,cm,\,\,BC = 2\,cm.\) Tính các tỉ số lượng giác \(\sin B;\cos B\)
Đáp án : B Phương pháp giải :
Bước 1: Tính cạnh còn lại theo định lý Pytago Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn Lời giải chi tiết :
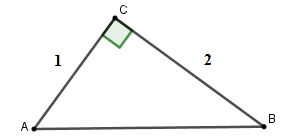 Theo định lý Py-ta-go ta có: \(A{B^2} = A{C^2} + B{C^2} \Rightarrow AB = \sqrt {{1^2} + {2^2}} = \sqrt 5 \) Xét tam giác \(ABC\) vuông tại \(C\) có \(\sin B = \dfrac{{AC}}{{AB}} = \dfrac{1}{{\sqrt 5 }} = \dfrac{{\sqrt 5 }}{5}\) và \(\cos B = \dfrac{{BC}}{{AB}} = \dfrac{2}{{\sqrt 5 }} = \dfrac{{2\sqrt 5 }}{5}\)
Câu 24 :
Cho \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo tỉ số \(\dfrac{3}{5}\) và chu vi của \(\Delta A'B'C'\) là $60cm.$ Khi đó chu vi \(\Delta ABC\) là:
Đáp án : C Phương pháp giải :
Ta có: \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số \(k\)\( \Rightarrow \dfrac{{{C_{\Delta ABC}}}}{{{C_{\Delta A'B'C'}}}} = \dfrac{{AB}}{{A'B'}} = k.\) Lời giải chi tiết :
Cho \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo tỉ số \(\dfrac{3}{5}\). \( \Rightarrow \dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{3}{5}\)\( \Rightarrow \dfrac{{{C_{\Delta ABC}}}}{{{C_{\Delta A'B'C'}}}} = \dfrac{3}{5} \Rightarrow {C_{\Delta ABC}} = \dfrac{3}{5}{C_{\Delta A'B'C'}}.\) Mà chu vi của tam giác \({C_{\Delta A'B'C'}} = 60cm\) nên \({C_{\Delta ABC}} = \dfrac{3}{5}. 60 = 36cm\).
Câu 25 :
Chọn khẳng định đúng. Nếu phương trình \(a{x^2} = mx + n\) có hai nghiệm phân biệt thì đường thẳng \(d:y = mx + n\) và parabol \(\left( P \right):y = a{x^2}\)
Đáp án : A Lời giải chi tiết :
Đường thẳng \(d:y = mx + n\) và parabol \(\left( P \right):y = a{x^2}\) cắt nhau tại hai điểm phân biệt khi phương trình \(a{x^2} = mx + n\) có hai nghiệm phân biệt.
Câu 26 :
Nếu \(\Delta ABC\) vuông tại A có \(BH = 9,HC = 25\) thì đường cao \(AH\) có độ dài là: 
Đáp án : A Phương pháp giải :
Sử dụng hệ thức lượng trong tam giác vuông: “Bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền”. Lời giải chi tiết :
Xét tam giác \(ABC\) vuông tại \(A\) có chiều cao \(AH.\) Theo hệ thức lượng trong tam giác vuông ta có: \(A{H^2} = HB.HC \Leftrightarrow A{H^2} = 9.25\) \( \Leftrightarrow A{H^2} = 225 \Rightarrow AH = 15\) Vậy \(AH = 15\,cm.\)
Câu 27 :
Đưa thừa số \(5x\sqrt {\dfrac{{ - 12}}{{{x^3}}}} \) (\(x < 0\)) vào trong dấu căn ta được:
Đáp án : C Phương pháp giải :
Đưa thừa số vào trong dấu căn +) \(A\sqrt B = \sqrt {{A^2}B} \) với \(A \ge 0\) và \(B \ge 0\) +) \(A\sqrt B = - \sqrt {{A^2}B} \) với \(A < 0\) và \(B \ge 0\) Lời giải chi tiết :
Ta có: \(5x\sqrt {\dfrac{{ - 12}}{{{x^3}}}} \)\( = - \sqrt {{{\left( {5x} \right)}^2}.\dfrac{{ - 12}}{{{x^3}}}} = \sqrt {25{x^2}\left( {\dfrac{{ - 12}}{x^3}} \right)} = - \sqrt {\dfrac{{ - 300}}{x}} \).
Câu 28 :
Giải phương trình \(\dfrac{{x - 1}}{{x + 2}} - \dfrac{{1 - x}}{{2 - x}} = \dfrac{{2({x^2} + 2)}}{{{x^2} - 4}}\) ta được tập nghiệm là:
Đáp án : A Phương pháp giải :
Giải phương trình chứa ẩn ở mẫu: Bước 1: Tìm điều kiện xác định của phương trình. Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu. Bước 3: Giải phương trình vừa nhận được. Bước 4: (Kết luận) Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho. Lời giải chi tiết :
ĐKXĐ: \(x \ne 2;\,\,x \ne - 2\) \(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{{x - 1}}{{x + 2}} - \dfrac{{1 - x}}{{2 - x}} = \dfrac{{2({x^2} + 2)}}{{{x^2} - 4}}\\ \Leftrightarrow \dfrac{{x - 1}}{{x + 2}} + \dfrac{{1 - x}}{{x - 2}} = \dfrac{{2({x^2} + 2)}}{{(x - 2)(x + 2)}}\\ \Leftrightarrow \dfrac{{(x - 1)(x - 2)}}{{(x - 2)(x + 2)}} + \dfrac{{(1 - x)(x + 2)}}{{(x - 2)(x + 2)}} = \dfrac{{2({x^2} + 2)}}{{(x - 2)(x + 2)}}\\ \Rightarrow (x - 1)(x - 2) + (1 - x)(x + 2) = 2({x^2} + 2)\\ \Leftrightarrow {x^2} - 2x - x + 2 + x + 2 - {x^2} - 2x = 2{x^2} + 4\\ \Leftrightarrow 2{x^2} + 4x = 0\\ \Leftrightarrow 2x(x + 2) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\,\,\,(TM)\\x = - 2\,\,\,\,\,(KTM)\end{array} \right.\end{array}\) Vậy tập nghiệm của phương trình là \(S = \left\{ 0 \right\}.\)
Câu 29 :
Thu gọn $\sqrt[3]{{ - \dfrac{1}{{27{a^3}}}}}$ với $a \ne 0$ ta được
Đáp án : C Phương pháp giải :
Sử dụng công thức $\sqrt[3]{{{a^3}}} = a$ Lời giải chi tiết :
Ta có $\sqrt[3]{{ - \dfrac{1}{{27{a^3}}}}} = \sqrt[3]{{{{\left( { - \dfrac{1}{{3a}}} \right)}^3}}} = - \dfrac{1}{{3a}}$
Câu 30 :
Không tính cụ thể, bất đẳng thức nào sau đây là bất đẳng thức sai?
Đáp án : B Phương pháp giải :
Áp dụng các tính chất: - Khi cộng cùng một số vào hai vế của một bất đẳng thức ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho. - Khi nhân cả hai vế của một bất đẳng thức với một số dương ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho. - Khi nhân cả hai vế của một bất đẳng thức với một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho. Lời giải chi tiết :
Ta có: +) \( - 2.3 = - 6\). Mà \( - 6 = - 6\). Vậy bất đẳng thức \( - 2.3 \ge - 6\) là đúng. +) Ta có: \(2 < 3\) nên \(2.\left( { - 3} \right) > 3.\left( { - 3} \right)\). Vậy bất đẳng thức \(2.( - 3) \le 3.( - 3)\) là sai. +) Ta có: \(2 > 1\) nên \(2 + ( - 5) > ( - 5) + 1\). Vậy bất đẳng thức \(2 + ( - 5) > ( - 5) + 1\) là đúng. + Ta có: \( - 3 > - 4\) nên \(2.( - 4) - 3 > 2.( - 4) - 4\). Vậy bất đẳng thức \(2.( - 4) - 3 > 2.( - 4) - 4\) là đúng.
Câu 31 :
Giá trị của biểu thức \(\sqrt {17 - 12\sqrt 2 } + \sqrt {9 + 4\sqrt 2 } \).
Đáp án : B Phương pháp giải :
- Đưa biểu thức dưới dấu căn về hằng đẳng thức \({a^2} - 2ab + {b^2} = {\left( {a - b} \right)^2};\)\({a^2} + 2ab + {b^2} = {\left( {a + b} \right)^2}\) - Sử dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,khi\,\,A \ge 0\\ - A\,\,khi\,\,A < 0\end{array} \right.\) - Cộng trừ các căn thức bậc hai. Lời giải chi tiết :
\(\sqrt {17 - 12\sqrt 2 } + \sqrt {9 + 4\sqrt 2 } \)\( = \sqrt {17 - 2.6\sqrt 2 } + \sqrt {9 + 2.2\sqrt 2 } = \sqrt {9 - 2.3.2\sqrt 2 + 8} + \sqrt {8 + 2.2\sqrt 2 .1 + 1} \) \( = \sqrt {{{\left( {3 - 2\sqrt 2 } \right)}^2}} + \sqrt {{{\left( {2\sqrt 2 + 1} \right)}^2}} = \left| {3 - 2\sqrt 2 } \right| + \left| {2\sqrt 2 + 1} \right| = 3 - 2\sqrt 2 + \left( {2\sqrt 2 + 1} \right) = 4.\)
Câu 32 :
Tìm hệ số góc của đường thẳng \(d\) biết \(d\) đi qua điểm \(M\left( { - 3;2} \right)\) và \(N\left( {1; - 1} \right)\).
Đáp án : D Phương pháp giải :
Bước 1: Viết phương trình đường thẳng \(d\) Bước 2: Xác định hệ số góc: đường thẳng \(d\) có phương trình \(y = ax + b\,\left( {a \ne 0} \right)\) có \(a\) là hệ số góc. Lời giải chi tiết :
Gọi \(d:y = {\rm{ax}} + b\,\left( {a \ne 0} \right)\) đi qua \(2\) điểm \(M\left( { - 3;2} \right)\) và \(N\left( {1; - 1} \right)\) \(M\) thuộc \(d \Leftrightarrow - 3a + b = 2 \Rightarrow b = 2 + 3a\,\,\left( 1 \right)\) \(N\) thuộc \(d \Leftrightarrow 1.a + b = - 1 \Leftrightarrow b = - 1 - a\,\,\left( 2 \right)\) Từ (1) và (2) suy ra \(2 + 3a = - 1 - a \Leftrightarrow 4a = - 3 \Leftrightarrow a = - \dfrac{3}{4}\) suy ra \(b = - 1 - a = - 1 + \dfrac{3}{4} = - \dfrac{1}{4}\) Vậy \(d:y = - \dfrac{3}{4}x - \dfrac{1}{4}\). Hệ số góc của \(d\) là \(k = - \dfrac{3}{4}\)
Câu 33 :
“Trong các dây của một đường tròn, đường kính là dây có độ dài…”. Cụm từ thích hợp điền vào chỗ trống là:
Đáp án : B Lời giải chi tiết :
Trong các dây của một đường tròn, đường kính là dây có độ dài lớn nhất.
Câu 34 :
Hình lập phương có thể tích \(512c{m^3}\) thì có diện tích toàn phần là:
Đáp án : A Phương pháp giải :
Tìm số \(a\) sao cho \(a.a.a = 512\), khi đó \(a\) là độ dài cạnh hình lập phương đó. Tính diện tích toàn phần ta lấy cạnh nhân với cạnh rồi nhân với \(6\). Lời giải chi tiết :
Ta có: \(8. 8. 8 = 512\) nên độ dài hình lập phương đã cho có cạnh là \(8cm\). Diện tích toàn phần của hình lập phương đã cho là: \(8 \times 8 \times 6 = 384\,\,(c{m^2})\). Vậy hình lập phương có thể tích \(512c{m^3}\) thì có diện tích toàn phần là \(384c{m^2}\).
Câu 35 :
Giá trị của biểu thức \(2\sqrt {32} - \sqrt {27} - 4\sqrt 8 + 3\sqrt {75} \) là:
Đáp án : C Phương pháp giải :
- Sử dụng công thức khai phương một tích \(\sqrt {AB} = \sqrt A .\sqrt B ,\,\,\left( {A,B \ge 0} \right)\) đưa biểu thức về các căn thức cùng loại (cùng biểu thức dưới dấu căn). - Sử dụng \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,khi\,A \ge 0\\ - A\sqrt B \,khi\,A < 0\end{array} \right.\) - Cộng trừ các căn thức. Lời giải chi tiết :
\(2\sqrt {32} - \sqrt {27} - 4\sqrt 8 + 3\sqrt {75} \)\( = 2\sqrt {16.2} - \sqrt {9.3} - 4\sqrt {4.2} + 3\sqrt {25.3} \)\(= 8\sqrt 2 - 3\sqrt 3 - 8\sqrt 2 + 15\sqrt 3 = 12\sqrt 3 \)
Câu 36 :
Cho phương trình \({x^2} - 2\left( {m - 1} \right)x + 2{m^2} - 3m + 1 = 0\), với \(m\) là tham số. Gọi \({x_1},{x_2}\) là nghiệm của phương trình. Chọn câu đúng.
Đáp án : A Phương pháp giải :
+ Sử dụng hệ thức Vi-et để biến đổi và đánh giá \(\left| {{x_1} + {x_2} + {x_1}{x_2}} \right|.\) Lời giải chi tiết :
Ta có \(\Delta ' = {\left( {m - 1} \right)^2} - \left( {2{m^2} - 3m + 1} \right) = - {m^2} + m = m\left( {1 - m} \right)\). Để phương trình có hai nghiệm \( \Leftrightarrow \Delta ' \ge 0 \Leftrightarrow 0 \le m \le 1\). Theo định lý Viet ta có: \({x_1} + {x_2} = 2\left( {m - 1} \right)\) và \({x_1}{x_2} = 2{m^2} - 3m + 1\). Ta có \(\left| {{x_1} + {x_2} + {x_1}{x_2}} \right| = \left| {2\left( {m - 1} \right) + 2{m^2} - 3m + 1} \right|\)\( = \left| {2{m^2} - m - 1} \right| = 2\left| {{m^2} - \dfrac{m}{2} - \dfrac{1}{2}} \right| = 2\left| {{{\left( {m - \dfrac{1}{4}} \right)}^2} - \dfrac{9}{{16}}} \right|\) Vì \(0 \le m \le 1 \Leftrightarrow - \dfrac{1}{4} \le m - \dfrac{1}{4} \le \dfrac{3}{4}\) suy ra \({\left( {m - \dfrac{1}{4}} \right)^2} \le \dfrac{9}{{16}} \Leftrightarrow {\left( {m - \dfrac{1}{4}} \right)^2} - \dfrac{9}{{16}} \le 0\) Do đó \(\left| {{x_1} + {x_2} + {x_1}{x_2}} \right| = 2\left| {{{\left( {m - \dfrac{1}{4}} \right)}^2} - \dfrac{9}{{16}}} \right| = 2\left| {\dfrac{9}{{16}} - {{\left( {m - \dfrac{1}{4}} \right)}^2}} \right| = \dfrac{9}{8} - 2{\left( {m - \dfrac{1}{4}} \right)^2} \le \dfrac{9}{8}\) Dấu “=” xảy ra khi và chỉ khi \(m = \dfrac{1}{4}\).
Câu 37 :
Hình vẽ bên là đồ thị của hàm số nào dưới đây? 
Đáp án : A Phương pháp giải :
Sử dụng cách vẽ đồ thị hàm số Đồ thị hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) là một đường thẳng Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\) Lời giải chi tiết :
Từ hình vẽ suy ra đồ thị hàm số đi qua hai điểm có tọa độ \(\left( {0; - 1} \right)\) và \(\left( {2;3} \right)\) . Thay tọa độ hai điểm vào mỗi hàm số ta thấy với hàm số \(y = 2x - 1\) +) Thay \(x = 0;y = - 1\) và vào hàm số \(y = 2x - 1\) ta được \( - 1 = 2.0 - 1 \Leftrightarrow - 1 = - 1\) (luôn đúng) +) Thay \(x = 2;y = 3\) và vào hàm số \(y = 2x - 1\) ta được \(3 = 2.2 - 1 \Leftrightarrow 3 = 3\) (luôn đúng) Vậy đồ thị hàm số \(y = 2x - 1\) là đường thẳng như hình vẽ.
Câu 38 :
Trong các hàm số \(y = - 3x + 2;y = - \dfrac{1}{3}\left( { - x + 1} \right);y = 6 - \dfrac{x}{2};y = - \left( {1 - 2x} \right)\), có bao nhiêu hàm số nghịch biến?
Đáp án : D Phương pháp giải :
Hàm số bậc nhất \(y = ax + b\) xác định với mọi giá trị của \(x\) thuộc \(\mathbb{R}\)và có tính chất sau - Đồng biến trên \(\mathbb{R}\) nếu \(a > 0\). - Nghịch biến trên \(\mathbb{R}\) nếu \(a < 0\). Lời giải chi tiết :
Hàm số \(y = - 3x + 2\) có \(a = - 3 < 0\) nên là hàm số nghịch biến Hàm số \(y = - \dfrac{1}{3}\left( { - x + 1} \right)\)\( \Leftrightarrow y = \dfrac{1}{3}x - \dfrac{1}{3}\) có \(a = \dfrac{1}{3} > 0\) nên là hàm số đồng biến Hàm số \(y = 6 - \dfrac{x}{2}\)\( \Leftrightarrow y = - \dfrac{1}{2}x + 6\)có \(a = - \dfrac{1}{2} < 0\) nên là hàm số nghịch biến Hàm số \(y = - \left( {1 - 2x} \right) \Leftrightarrow y = 2x - 1\) có \(a = 2 > 0\) nên là hàm số đồng biến Vậy có hai hàm số nghịch biến \(y = - 3x + 2;y = 6 - \dfrac{x}{2}.\)
Câu 39 :
Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy \(S = 36\pi \,c{m^2}\) và chiều cao \(h = 8\,cm\) . Nếu trục lăn đủ \(10\) vòng thì diện tích tạo trên sân phẳng là bao nhiêu? 
Đáp án : C Phương pháp giải :
Sử dụng diện tích đáy $S_đ=\pi.R^2$ để tính bán kính \(R\) . Sử dụng công thức tính diện tích xung quanh của hình trụ \({S_{xq}} = 2\pi Rh\) Lời giải chi tiết :
Bán kính \(R\) của đường tròn đáy là \(\pi {R^2} = 36\pi\) suy ra \(R = 6\,cm\) Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi Rh = 2\pi .6.8 = 96\pi \,\left( {c{m^2}} \right)\) Vì trục lăn \(10\) vòng nên diện tích tạo trên sân phẳng là \(10.96\pi = 960\pi \,\left( {c{m^2}} \right)\)
Câu 40 :
Tìm giá trị nhỏ nhất của biểu thức \(A = \sqrt {{m^2} + 2m + 1} + \sqrt {{m^2} - 8m + 16} \).
Đáp án : C Phương pháp giải :
- Đưa biểu thức dưới dấu căn thành hằng đẳng thức. - Sử dụng hằng đẳng thức $\sqrt {{A^2}} = \left| A \right|$ - Sử dụng bất đẳng thức \(\left| A \right| + \left| B \right| \ge \left| {A + B} \right|\) với mọi \(A,B.\) Dấu ‘=’ xảy ra \( \Leftrightarrow A = B\) Lời giải chi tiết :
Ta có \(A = \sqrt {{m^2} + 2m + 1} + \sqrt {{m^2} - 8m + 16} \)\( = \sqrt {{{\left( {m + 1} \right)}^2}} + \sqrt {{{\left( {m - 4} \right)}^2}} = \left| {m + 1} \right| + \left| {m - 4} \right|\) Ta có \(\left| {m + 1} \right| + \left| {m - 4} \right| = \left| {m + 1} \right| + \left| {4 - m} \right| \ge \left| {m + 1 + 4 - m} \right| = 5\) Dấu “=” xảy ra khi \(m + 1 = 4 - m \) hay \( 2m = 3 \Leftrightarrow m = \dfrac{3}{2}\) Suy ra GTNN của \(B\) là \(5 \) khi \( m = \dfrac{3}{2}\) . |