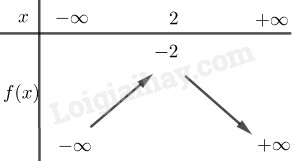
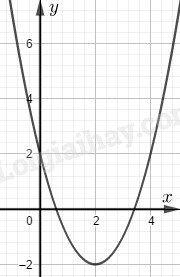
Giải đề thi học kì 1 môn Toán lớp 10 trường THPT Lương Văn Can năm 2020-2021

Đề bài

Câu 1(1 điểm). Tìm tập xác định của hàm số \(y = \dfrac{{{x^2} + x + 4}}{{\left( {{x^2} - 9} \right)\sqrt {x - 2} }}\)

Câu 2(1 điểm). Lập bảng biến thiên và vẽ đồ thị của hàm số \(y = {x^2} - 4x + 2\)

Câu 3( 2 điểm). Cho phương trình \({x^2} - \left( {2m + 1} \right)x + {m^2} + 2 = 0\)(1)

a) Tìm m để phương trình (1) có nghiệm \(x = 2\) và tính nghiệm còn lại

b) Tìm m để phương trình (1) có 2 nghiệm phân biệt \({x_1},{x_2}\) thỏa: \(3{x_1}{x_2} - 5\left( {{x_1} + {x_2}} \right) + 6 = 0\)

Câu 4 (3 điểm) Giải các phương trình sau:

a) \(\dfrac{{3x}}{{x + 1}} + \dfrac{{x - 1}}{x} = \dfrac{{2x + 1}}{{x\left( {x + 1} \right)}}\)

b) \(\left| {{x^2} - 1} \right| = 1 - 4x\)

c) \(\sqrt {{x^2} - 2x + 2}  = 2x - 1\)

Câu 5(3 điểm). Trong mặt phẳng tọa độ Oxy cho tam giác ABC có \(A\left( { - 1;2} \right),B\left( {5;4} \right),C\left( {0;9} \right)\).

a) Chứng minh tam giác ABC cân tại C

b) Tìm tọa độ của điểm G là trọng tâm tam giác ABC

c) Tìm tọa độ trực tâm H của tam giác ABC.

Lời giải chi tiết

Câu 1(TH)

Phương pháp:

+) \(\dfrac{{f\left( x \right)}}{{g\left( x \right)}}\) xác định nếu \(g\left( x \right) \ne 0\).

+) \(\dfrac{1}{\sqrt {f\left( x \right)}} \) xác định nếu \(f\left( x \right) > 0\).

Lời giải:

Điều kiện xác định của hàm số :

\(\left\{ \begin{array}{l}{x^2} - 9 \ne 0\\x - 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne  \pm 3\\x > 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 3\\x > 2\end{array} \right.\)

Vậy tập xác định của hàm số là :\(D = \left( {2; + \infty } \right)\backslash \left\{ 3 \right\}\)

Câu 2(TH)

Phương pháp:

Nếu \(a > 0\), hàm số đồng biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\).

Nếu \(a < 0\), hàm số đồng biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\) và nghịch biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\).

Vẽ đồ thị:

- Có dáng là đường Parabol có đỉnh \(\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right),\Delta  = {b^2} - 4ac\).

- Trục đối xứng là đường thẳng \(x =  - \dfrac{b}{{2a}}\).

- Bề lõm hướng lên trên khi \(a > 0\) và hướng xuống dưới khi \(a < 0\)

Lời giải:

Ta có \( - \dfrac{b}{{2{\rm{a}}}} =  - \dfrac{{ - 4}}{{2.1}} = 2\).

Hàm số đồng biến trên \(\left( {2; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;2} \right)\).

Bảng biến thiên:

Đồ thị:

Đồ thị nhận đường thẳng \(x = 2\) làm trục đối xứng. Thay \(x = 2\) vào hàm số ta được \(y =  - 2\). Đỉnh của đồ thị là \(I\left( {2; - 2} \right)\). Đồ thị có bề lõm hướng lên trên.

Đồ thị hàm số cắt trục tung tại \(A\left( {0;2} \right)\) và đi qua các điểm \(B\left( {1; - 1} \right),C\left( {4;2} \right);D\left( { - 1;7} \right)\)

Câu 3(VD)

Phương pháp:

a) Thay x=2 vào phương trình tìm m rồi thay m vào phương trình ban đầu tìm nghiệm thứ hai

b) Phương trình \(a{x^2} + bx + c = 0\) có 2 nghiệm phân biệt khi và chỉ khi \(\Delta  > 0\).

Sử dụng định lý Viét:

\({x_1},{x_2}\) là 2 nghiệm của phương trình \(a{x^2} + bx + c = 0\). Khi đó:

\(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)

Lời giải:

a) Thay \(x = 2\) vào phương trình (1) ta được: \({2^2} - \left( {2m + 1} \right).2 + {m^2} + 2 = 0\)

\(\begin{array}{l} \Leftrightarrow {m^2} - 4m + 4 = 0\\ \Leftrightarrow {\left( {m - 2} \right)^2} = 0 \Leftrightarrow m = 2\end{array}\)

Thay \(m = 2\) vào phương trình (1) ta được: \({x^2} - (2.2 + 1)x + {2^2} + 2 = 0\)

\( \Leftrightarrow {x^2} - 5x + 6 = 0\)

\(\begin{array}{l} \Leftrightarrow \left( {x - 2} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 3\end{array} \right.\end{array}\)

Vậy nghiệm thứ hai của phương trình là \(x = 3\)

b) Phương trình (1) có 2 nghiệm phân biệt khi và chỉ khi \(\Delta  > 0\)

\(\begin{array}{l} \Leftrightarrow {\left( {2m + 1} \right)^2} - 4\left( {{m^2} + 2} \right) > 0\\ \Leftrightarrow 4m - 7 > 0 \Leftrightarrow m > \dfrac{7}{4}\end{array}\)

Giả sử (1) có 2 nghiệm phân biệt \({x_1},{x_2}\), theo định lý Viét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = {m^2} + 2\end{array} \right.\).

Thay vào phương trình  \(3{x_1}{x_2} - 5\left( {{x_1} + {x_2}} \right) + 6 = 0\). Ta được:

\(\begin{array}{l}3.\left( {{m^2} + 2} \right) - 5\left( {2m + 1} \right) + 6 = 0\\ \Leftrightarrow 3{m^2} - 10m + 7 = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = \dfrac{7}{3}\end{array} \right.(ktm)\end{array}\)

Vậy không tồn tại giá trị của m thỏa mãn đề bài.

Câu 4(VD)

Phương pháp:

a)

- Bước 1: Đặt điều kiện xác định:

\(\dfrac{{f\left( x \right)}}{{g\left( x \right)}}\) xác định nếu \(g\left( x \right) \ne 0\).

- Bước 2: Quy đồng mẫu thức, khử mẫu và giải phương trình thu được.

- Bước 3: Kiểm tra điều kiện và kết luận nghiệm.

b) Giải phương trình bằng cách phá dấu giá trị tuyệt đối

\(\begin{array}{l}\left| {f\left( x \right)} \right| = g\left( x \right)\\ \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = g\left( x \right){\rm{ khi }}f\left( x \right) \ge 0\\f\left( x \right) =  - g\left( x \right){\rm{ khi }}f\left( x \right) < 0\end{array} \right.\end{array}\)

c) Giải phương trình chứa căn thức bậc hai:

\(\sqrt {f\left( x \right)}  = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = 0\end{array} \right.\)

Lời giải:

a) \(\dfrac{{3x}}{{x + 1}} + \dfrac{{x - 1}}{x} = \dfrac{{2x + 1}}{{x\left( {x + 1} \right)}}\)(1)

Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 1;0} \right\}\)

\(\left( 1 \right) \Leftrightarrow \dfrac{{3x.x}}{{\left( {x + 1} \right).x}} + \dfrac{{\left( {x - 1} \right).\left( {x + 1} \right)}}{{x\left( {x + 1} \right)}} \\= \dfrac{{2x + 1}}{{x\left( {x + 1} \right)}}\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{3{x^2} + \left( {{x^2} - 1} \right)}}{{x\left( {x + 1} \right)}} = \dfrac{{2x + 1}}{{x\left( {x + 1} \right)}}\\ \Rightarrow 4{x^2} - 1 = 2x + 1\\ \Leftrightarrow 4{x^2} - 2x - 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \dfrac{{ - 1}}{2}\end{array} \right.\left( {tm} \right)\end{array}\)

Vậy tập nghiệm của phương trình là \({\rm{S}} = \left\{ { - \dfrac{1}{2};1} \right\}\)

b)

TH1: \({x^2} - 1 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 1\\x \le  - 1\end{array} \right.\)

\(\left| {{x^2} - 1} \right| = 1 - 4x\)

\(\begin{array}{l} \Leftrightarrow {x^2} - 1 = 1 - 4x\\ \Leftrightarrow {x^2} + 4x - 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 2 + \sqrt 6 (ktm)\\x =  - 2 - \sqrt 6 (tm)\end{array} \right.\end{array}\)

TH2: \({x^2} - 1 < 0 \Leftrightarrow  - 1 < x < 1\)

\(\left| {{x^2} - 1} \right| = 1 - 4x\)

\(\begin{array}{l} \Leftrightarrow {x^2} - 1 = 4x - 1\\ \Leftrightarrow {x^2} - 4x = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\left( {tm} \right)\\x = 4\left( {ktm} \right)\end{array} \right.\end{array}\)

Vậy tập nghiệm của phương trình đã cho là \({\rm{S}} = \left\{ {0; - 2 - \sqrt 6 } \right\}\)

c) \(\sqrt {{x^2} - 2x + 2}  = 2x - 1\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}2x - 1 \ge 0\\{x^2} - 2x + 2 = {\left( {2x - 1} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{1}{2}\\3{x^2} - 2x - 1 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{1}{2}\\x = 1\\x =  - \dfrac{1}{3}\end{array} \right. \Leftrightarrow x = 1\end{array}\)

Vậy tập nghiệm của phương trình là \(S = \left\{ 1 \right\}\)

Câu 5(VD).

Phương pháp:

a) Tính độ dài đoạn thẳng CA và CB rồi so sánh.

Sử dụng công thức độ dài đoạn thẳng AB với \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\):

\(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \)

b) Trọng tâm tam giác ABC:

\(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\)

c) Gọi tọa độ điểm \(H\left( {{x_0};{y_0}} \right)\). Sử dụng \(\overrightarrow {AH} .\overrightarrow {BC}  = 0\) và \(\overrightarrow {BH} .\overrightarrow {AC}  = 0\) tìm \({{\rm{x}}_0},{y_0}\).

Lời giải:

a)

\(\begin{array}{l}AC = \sqrt {{{\left( {{x_C} - {x_A}} \right)}^2} + {{\left( {{y_C} - {y_A}} \right)}^2}} \\ = \sqrt {{1^2} + {7^2}}  = 5\sqrt 2 \end{array}\)

\(\begin{array}{l}CB = \sqrt {{{\left( {{x_B} - {x_C}} \right)}^2} + {{\left( {{y_B} - {y_C}} \right)}^2}} \\ = \sqrt {{5^2} + {{\left( { - 5} \right)}^2}}  = 5\sqrt 2 \end{array}\)

\( \Rightarrow AC = CB \Rightarrow \Delta ABC\) cân tại C.

b) G là trọng tâm tam giác ABC nên:

\(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3} = \dfrac{4}{3}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3} = 5\end{array} \right.\)

Vậy trọng tâm tam giác ABC là \(G\left( {\dfrac{4}{3};5} \right)\)

c) Gọi tọa độ điểm \(H\left( {{x_0};{y_0}} \right)\).

Ta có

 \(\begin{array}{l}\overrightarrow {AH}  = \left( {{x_H} - {x_A},{y_H} - {y_A}} \right)\\ = \left( {{x_0} + 1;{y_0} - 2} \right)\end{array}\)

\(\overrightarrow {BC}  = \left( { - 5;5} \right)\); \(BH = \left( {{x_0} - 5;{y_0} - 4} \right)\); \(\overrightarrow {AC}  = \left( {1;7} \right)\).

\(\begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC}  = 0\\ \Leftrightarrow \left( {{x_0} + 1} \right).\left( { - 5} \right) + \left( {{y_0} - 2} \right).5 = 0\\ \Leftrightarrow  - 5{x_0} + 5{y_0} = 15 \Leftrightarrow {x_0} - {y_0} =  - 3\end{array}\)

\(\begin{array}{l}\overrightarrow {BH} .\overrightarrow {AC}  = 0\\ \Leftrightarrow \left( {{x_0} - 5} \right).1 + \left( {{y_0} - 4} \right).7 = 0\\ \Leftrightarrow {x_0} + 7{y_0} = 33\end{array}\)

Ta được hệ:  

\(\left\{ \begin{array}{l}{x_0} - {y_0} =  - 3\\{x_0} + 7{y_0} = 33\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = \dfrac{3}{2}\\{y_0} = \dfrac{9}{2}\end{array} \right.\)

Vậy \(H\left( {\dfrac{3}{2};\dfrac{9}{2}} \right)\)

HocTot.Nam.Name.Vn