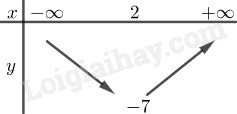
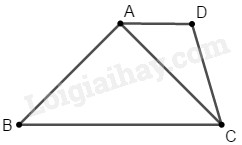
Giải đề thi học kì 1 toán lớp 10 năm 2020-2021 trường THPT Chuyên Lê Hồng Phong, TP. HCM

Đề bài

Câu 1(1 điểm). Cho \(\left( P \right):y = a{x^2} + bx + c\). Tìm \(a,b,c\) biết \(\left( P \right)\) có trục đối xứng là đường thẳng \({\rm{x}} = 2\) và (P) đi qua điểm \(A\left( {0;1} \right),B\left( {1; - 2} \right)\).

Câu 2(1 điểm). Giải phương trình \(\sqrt {{x^2} - 3x + 2}  = x - 1\)

Câu 3(1 điểm). Cho hệ phương trình \(\left\{ \begin{array}{l}\left( {m + 1} \right)x + 6y = {m^2} + 3m + 5\\x + my = {m^3} - 3\end{array} \right.\)

Tìm tất cả các giá trị của tham số \(m\) sao cho hệ phương trình có nghiệm.

Câu 4(1 điểm). Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 5\\{x^2} + {y^2} + 3xy = 11\end{array} \right.\)

Câu 5(1 điểm). Cho phương trình \(\dfrac{{2{x^2} - 8x + m}}{{{x^2} - 4x + 3}} = 1\). Tìm tất cả các giá trị của tham số m để phương trình có nghiệm.

Câu 6(3 điểm). Trong mặt phẳng Oxy, cho tam giác ABC biết \(A\left( {2; - 1} \right),B\left( {1;2} \right),C\left( {4;3} \right)\).

a) Chứng minh ABC là tam giác vuông cân.

b) Tìm giao điểm của đường thẳng AB và trục tung.

c) Tìm tọa độ điểm D sao cho ABCD là hình thang có \(AD//BC\) và diện tích ABCD bằng 15.

Câu 7(1 điểm). Cho hình vuông ABCD cạnh a, gọi I là giao điểm của AC và BD, M là điểm thỏa mãn \(M{A^2} + 2M{B^2} + M{C^2} + 2M{{\rm{D}}^2} = 12{{\rm{a}}^2}\), tính MI.

Câu 8(1 điểm). Cho các số thực x,y thỏa mãn \({{\rm{x}}^2} + {y^2} + xy = 3\). Tìm giá trị lớn nhất, giá trị nhỏ nhất của \(P = {x^4} + {y^4} + 2\left( {{x^2} + {y^2}} \right) + 12xy\).

Lời giải chi tiết

Câu 1(VD).

Phương pháp:

Hàm số \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\) nhận đường thẳng \(x =  - \dfrac{b}{{2a}}\) làm trục đối xứng.

(P) đi qua \(A\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0} + b{x_0} + c\).

Lời giải:

\(\left( P \right)\) có trục đối xứng là đường thẳng \(x = 2\) nên \( - \dfrac{b}{{2{\rm{a}}}} = 2 \Leftrightarrow b =  - 4{\rm{a}}\).(1)

\(\left( P \right)\) đi qua \(A\left( {0;1} \right),B\left( {1; - 2} \right)\) nên ta có:

\(\left\{ \begin{array}{l}1 = c\\ - 2 = a + b + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a + b =  - 3(2)\end{array} \right.\)

Từ (1) và (2) ta có :

\(\begin{array}{l}\left\{ \begin{array}{l}b =  - 4{\rm{a}}\\a + b =  - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b =  - 4{\rm{a}}\\ - 3{\rm{a}} =  - 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}b =  - 4{\rm{a}}\\a = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b =  - 4\\a = 1\end{array} \right.\end{array}\)

Vậy \(a = 1;b =  - 4;c = 1\)

Câu 2(VD).

Phương pháp:

\(\sqrt {f\left( x \right)}  = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\)

Lời giải:

\(\begin{array}{l}\sqrt {{x^2} - 3x + 2}  = x - 1\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} - 3x + 2 = {x^2} - 2x + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x = 1\end{array} \right. \Leftrightarrow x = 1\end{array}\)

Câu 3(VD)

Phương pháp:

Tìm điều kiện để hệ phương trình vô nghiệm rồi lấy phần bù.

Hệ vô nghiệm khi và chỉ khi \(\left\{ \begin{array}{l}D = \left| {\begin{array}{*{20}{c}}a&b\\{a'}&{b'}\end{array}} \right| = ab' - a'b = 0\\\left[ \begin{array}{l}{D_x} = cb' - c'b \ne 0\\{D_y} = ac' - a'c \ne 0\end{array} \right.\end{array} \right.\)

Lời giải:

Xét \(D = ab' - a'b = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}m = 2\\m =  - 3\end{array} \right.\)

Với \(m = 2\),  thì \({D_x} = {D_y} = 0\), hệ có vô số nghiệm.

Với \(m =  - 3\),

\(\begin{array}{l}{D_x} =  - 6\left( {{m^3} - 3} \right) + \left( {{m^2} + 3m + 5} \right).m\\ = 195 \ne 0\end{array}\)

\( \Rightarrow m =  - 3\) thì hệ vô nghiệm.

Câu 4(VD)

Phương pháp:

Sử dụng phương pháp thế. Rút \(x\) từ phương trình thứ nhất thế vào phương trình thứ hai.

Lời giải:

 \(\begin{array}{l}\left\{ \begin{array}{l}x + 2y = 5\\{x^2} + {y^2} + 3xy = 11\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 5 - 2y\\{\left( {5 - 2y} \right)^2} + {y^2} + 3.\left( {5 - 2y} \right).y = 11\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 5 - 2y\\ - {y^2} - 5y + 14 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 5 - 2y\\\left[ \begin{array}{l}y = 2\\y =  - 7\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}y = 2;x = 1\\y =  - 7;x = 19\end{array} \right.\end{array}\)

Câu 5.(VD)

Phương pháp:

Tìm điều kiện xác định của phương trình.

Quy đồng 2 vế của phương trình. Cô lập m và sử dụng bảng biến thiên để biện luận nghiệm.

Lời giải:

ĐKXĐ: \(x \ne 1;x \ne 3\)

\(\begin{array}{l}\dfrac{{2{x^2} - 8x + m}}{{{x^2} - 4x + 3}} = 1\\ \Leftrightarrow \dfrac{{2{x^2} - 8x + m - \left( {{x^2} - 4x + 3} \right)}}{{{x^2} - 4x + 3}} = 0\\ \Leftrightarrow \dfrac{{{x^2} - 4x - 3 + m}}{{{x^2} - 4x + 3}} = 0\\ \Rightarrow {x^2} - 4x - 3 + m = 0\left( 1 \right)\end{array}\)

Để hàm số đã cho có nghiệm thì \(\left( 1 \right)\) có nghiệm thỏa mãn điều kiện xác định, tức là:\(\left\{ \begin{array}{l}1 - 4 - 3 + m \ne 0\\{3^2} - 4.3 - 3 + m \ne 0\end{array} \right. \Leftrightarrow m \ne 6\)

Xét hàm số \(f\left( x \right) = {x^2} - 4x - 3\) có bảng biến thiên:

Từ bảng biến thiên ta có đường thẳng \(y =  - m\) cắt đồ thị khi và chỉ khi \( - m \ge  - 7 \Leftrightarrow m \le 7\).

Vậy phương trình ban đầu có nghiệm khi và chỉ khi \(m \le 7;m \ne 6\).

Câu 6.(VD)

Phương pháp:

a) Tìm \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \). So sánh độ dài các vectơ và tính tích vô hướng của các vectơ.

b) Viết phương trình đường thẳng qua A và B: đi qua A và nhận \(\overrightarrow {BC} \) làm vectơ pháp tuyến.

Điểm trên trục tung có dạng \(x = 0\)

c) Lập phương trình đường thẳng AD. Tham số hóa điểm D. Tìm điều kiện của D để ABCD là hình bình hành.

Lời giải:

a) \(\overrightarrow {AB}  = \left( { - 1;3} \right);\overrightarrow {AC}  = \left( {2;4} \right);\overrightarrow {BC}  = \left( {3;1} \right)\)

Ta có: \(AB = BC = \sqrt {10} ;\overrightarrow {AB} .\overrightarrow {BC}  = 0\).

Vậy \(\Delta ABC\) vuông cân tại B.

b)

\(\begin{array}{l}AB:3\left( {x - 2} \right) + 1\left( {y + 1} \right) = 0\\ \Leftrightarrow 3x + y - 5 = 0\end{array}\)

Giao điểm của AB và trục tung là \(M\left( {0;{y_M}} \right)\) khi đó \(3.0 + {y_M} - 5 = 0 \Leftrightarrow {y_M} = 5\)

Vậy \(M\left( {0;5} \right)\) là điểm cần tìm.

c)

\(\begin{array}{l}BC:1\left( {x - 1} \right) - 3\left( {y - 2} \right) = 0\\ \Leftrightarrow x - 3y + 5 = 0\end{array}\)

ABCD là hình thang có \(AD//BC\) nên phương trình đường thẳng AD  có dạng: \(1\left( {x - 2} \right) - 3\left( {y + 1} \right) = 0 \Leftrightarrow x - 3y - 5 = 0\). Khi đó tọa độ của D là:

\(D\left( {3d + 5;d} \right)\)

Do D và C phải cùng phía nhau so với AB nên \(\begin{array}{l}\left( {3.{x_C} + {y_C} - 5} \right)\left( {3{x_D} + {y_D} - 5} \right) > 0\\ \Leftrightarrow d >  - 1\\ \Rightarrow AD = \sqrt {{{\left( {3d + 5 - 2} \right)}^2} + {{\left( {d + 1} \right)}^2}} \\ = \sqrt {10} .\left( {d + 1} \right)\end{array}\)

Chiều cao của hình thang ABCD là \(d\left( {A,BC} \right) = \dfrac{{\left| {2 - 3.\left( { - 1} \right) + 5} \right|}}{{\sqrt {10} }} = \sqrt {10} \)

Diện tích ABCD là

\(\begin{array}{l}S = \dfrac{1}{2}.\sqrt {10} .\left( {BC + AD} \right)\\ = \dfrac{1}{2}\sqrt {10} .\left( {\sqrt {10}  + \left( {d + 1} \right)\sqrt {10} } \right)\\ = 5.\left( {d + 2} \right) = 15 \Rightarrow d = 1\end{array}\)

Vậy \(D\left( {8;1} \right)\)

Câu 7.(VD)

Phương pháp:

Công thức đường trung tuyến tam giác MAC với I là trung điểm AC: \(M{I^2} = \dfrac{{M{A^2} + M{C^2}}}{2} - \dfrac{{A{C^2}}}{4}\)

Chứng minh \(M{A^2} + M{C^2} = M{B^2} + M{D^2}\) và biểu diễn chúng theo a.

Lời giải:

Tam giác MAC với I là trung điểm AC có :\(M{I^2} = \dfrac{{M{A^2} + M{C^2}}}{2} - \dfrac{{A{C^2}}}{4}\).

Tương tự \(M{I^2} = \dfrac{{M{B^2} + M{D^2}}}{2} - \dfrac{{B{D^2}}}{4}\)

Vì \(AC = BD = a\sqrt 2 \) nên :\(M{A^2} + M{C^2} = M{B^2} + M{D^2}\)

\(\begin{array}{l} \Rightarrow 3\left( {M{A^2} + M{C^2}} \right) = 12{{\rm{a}}^2}\\ \Rightarrow M{A^2} + M{C^2} = 4{{\rm{a}}^2}\\ \Rightarrow M{I^2} = 2{{\rm{a}}^2} - \dfrac{{{a^2}}}{2} = \dfrac{{3{{\rm{a}}^2}}}{2}\\ \Rightarrow MI = \dfrac{{a\sqrt 6 }}{2}\end{array}\)

Câu 8(VDC).

Phương pháp:

Tìm điều kiện của \(xy\)

Biểu diễn \(P\) về hàm số bậc hai của \(xy\). Tìm GTLN, GTNN của hàm số này trên tập xác định của xy.

Lời giải:

\(\begin{array}{l}{x^2} + {y^2} + xy = 3\\ \Rightarrow \left\{ \begin{array}{l}{\left( {x + y} \right)^2} = 3 + xy \ge 0 \Rightarrow xy \ge  - 3\\{\left( {x - y} \right)^2} = 3 - 3xy \ge 0 \Rightarrow xy \le 1\end{array} \right.\\ \Rightarrow  - 3 \le xy \le 1\end{array}\)

\(\begin{array}{l}P = {x^4} + {y^4} + 2\left( {{x^2} + {y^2}} \right) + 12xy\\ = {\left( {{x^2} + {y^2}} \right)^2} - 2{x^2}{y^2} + 2\left( {{x^2} + {y^2}} \right) + 12xy\\ = {\left( {3 - xy} \right)^2} + 2\left( {3 - xy} \right) + 12xy - 2{x^2}{y^2}\\ =  - {x^2}{y^2} + 4xy + 15\end{array}\)

Đặt \(xy = t\)

\( \Rightarrow P = P\left( t \right) =  - {t^2} + 4t + 15\)

Ta tìm GTLN, GTNN của hàm số \(P\left( t \right)\) trên \(\left[ { - 3;1} \right]\)

Hàm số \(P\left( t \right)\) đồng biến trên \(\left( { - \infty ;2} \right)\) nên đồng biến trên \(\left[ { - 3;1} \right]\). Do đó,

\(\begin{array}{l}MaxP = P\left( 1 \right) = 18 \Leftrightarrow \left\{ \begin{array}{l}xy = 1\\x = y\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = y = 1\\x = y =  - 1\end{array} \right.\\MinP = P\left( { - 3} \right) =  - 6 \Leftrightarrow \left\{ \begin{array}{l}xy =  - 3\\x =  - y\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x =  - y = \sqrt 3 \\x =  - y =  - \sqrt 3 \end{array} \right.\end{array}\)

HocTot.Nam.Name.Vn