Đề thi giữa kì 2 Toán 10 Chân trời sáng tạo - Đề số 2

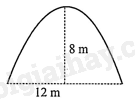
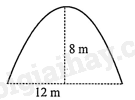
Đề bài

Phần trắc nghiệm (7 điểm)

Câu 1: Điều kiện để tam thức bậc hai \(a{x^2} + bx + c(a \ne 0)\) nhận giá trị âm với mọi \(x \in \mathbb{R}\) là:

A. \(\Delta  > 0\).

B. \(\Delta  < 0\).

C. \(\Delta  < 0\) và \(a > 0\).

D. \(\Delta  < 0\) và \(a < 0\).

Câu 2: Bảng xét dấu sau đây là của tam thức bậc hai nào?

 

A. \({x^2} - x + 6\).

B. \({x^2} + x + 6\).

C. \({x^2} - x - 6\).

D. \( - {x^2} + x - 6\).

Câu 3: Nghiệm của bất phương trình \({x^2} - 8x + 15 \le 0\) là:

A. \(x \in [3;5]\).

B. \(x \in (3;5)\).

C. \(x \in ( - \infty ;3] \cup [5; + \infty )\).

D. \(x \in ( - \infty ;3) \cup (5; + \infty )\).

Câu 4: Với giá trị nào của \(m\) thì bất phương trình \( - {x^2} - x + m \ge 0\) vô nghiệm?

A. \(m \ge  - \frac{1}{4}\).

B. \(m >  - \frac{1}{4}\).

C. \(m \le  - \frac{1}{4}\).

D. \(m <  - \frac{1}{4}\).

Câu 5: Một đường hầm xuyên thẳng qua núi và có mặt cắt là một parabol (thông số như hình bên). Giả sử một chiếc xe tải có chiều ngang \(6\;m\) đi vào vị trí chính giữa miệng hầm. Hỏi chiều cao \(h\) của xe tải cần thoả mãn điều kiện gì để có thể đi vào cửa hầm mà không chạm tường?

 

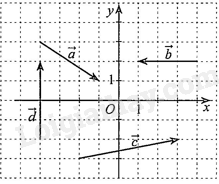
A. \(0 < h < 6\).

B. \(0 < h \le 6\).

C. \(0 < h < 7\).

D. \(0 < h \le 7\).

Câu 6: Giá trị nào của \(m\) thì phương trình \((m - 3){x^2} + (m + 3)x - (m + 1) = 0\) có hai nghiệm phân biệt?

A. \(m \in \left( { - \infty ; - \frac{3}{5}} \right) \cup (1; + \infty )\backslash \{ 3\} \).

B. \(m \in \left( { - \frac{3}{5};1} \right)\).

C. \(m \in \left( { - \frac{3}{5}; + \infty } \right)\).

D. \(m \in \mathbb{R}\backslash \{ 3\} \).

Câu 7: Tìm các giá trị của tham số \(m\) để bất phương trình \( - {x^2} + (2m - 1)x + m < 0\) có tập nghiệm là \(\mathbb{R}\).

A. \(m = \frac{1}{2}\).

B. \(m =  - \frac{1}{2}\).

C. \(m \in \mathbb{R}\).

D. Không tồn tại \(m\).

Câu 8: Với giá trị nào của \(m\) thì bất phương trình \({x^2} - x + m \le 0\) vô nghiệm?

A. \(m < 1\).

B. \(m > 1\).

C. \(m < \frac{1}{4}\).

D. \(m > \frac{1}{4}\).

Câu 9: Bất phương trình \({x^2} - (m + 2)x + m + 2 \le 0\) vô nghiệm khi và chỉ khi:

A. \(m \in ( - \infty ; - 2] \cup [2; + \infty )\).

B. \(m \in ( - \infty ; - 2) \cup (2; + \infty )\).

C. \(m \in [ - 2;2]\).

D. \(m \in ( - 2;2)\).

Câu 10: Xác định \(m\) để với mọi \(x\), ta có \( - 1 \le \frac{{{x^2} + 5x + m}}{{2{x^2} - 3x + 2}} < 7\).

A. \( - \frac{5}{3} \le m < 1\).

B. \(1 < m \le \frac{5}{3}\).

C. \(m \le  - \frac{5}{3}\).

D. \(m < 1\).

Câu 11: Xác định \(m\) để \((x - 1)\left[ {{x^2} + 2(m + 3)x + 4m + 12} \right] = 0\) có ba nghiệm phân biệt lớn hơn \( - 1\).

A. \(m <  - \frac{7}{2}\)

B. \( - 2 < m < 1\) và \(m \ne  - \frac{{16}}{9}\).

C. \( - \frac{7}{2} < m <  - 1\) và \(m \ne  - \frac{{16}}{9}\).

D. \( - \frac{7}{2} < m <  - 3\) và \(m \ne  - \frac{{19}}{6}\).

Câu 12: Tam thức bậc hai \(f(x) = {x^2} + (\sqrt 5  - 1)x - \sqrt 5 \) nhận giá trị dương khi?

A. \(x \in ( - \sqrt 5 ;1)\).

В. \(x \in ( - \infty ; - \sqrt 5 ) \cup (1; + \infty )\).

C. \(x \in ( - \sqrt 5 ; + \infty )\).

D. \(x \in ( - \infty ;1)\).

Câu 13: Cho phương trình \(\sqrt {{x^4} - 3{x^2} + 2}  = {x^2} + 2\). Nếu đặt \(t = {x^2},t \ge 0\) thì phương trình đã cho trở thành phương trình nào sau đây?

A. \(\sqrt {{t^2} - 3t + 2}  = {t^2} + 2\).

B. \(\sqrt {{t^2} - 3t + 2}  = t + 2\).

C. \(\sqrt {{t^2} - 3t + 2}  = t - 2\).

D. \(\sqrt {{t^2} + 3t - 2}  = t + 2\).

Câu 14: Số nghiệm của phương trình \(\sqrt {{x^2} - 4|x| + 3}  = 2x - 1\) là:

A. 1.

B. 2.

C. 4.

D. 0.

Câu 15: Tập nghiệm của phương trình \(\sqrt {{x^2} - 4x + 3}  = x + 1\) là:

A. \(S = \emptyset \).

B. \(S = \left\{ {\frac{1}{3}} \right\}\).

C. \(S = \{ 3\} \).

D. \(S = \{ 1\} \).

Câu 16: Số nghiệm của phương trình \(\sqrt {{x^2} - 3x + 2}  = \sqrt {2{x^2} - 7|x| + 4} \) là:

A. 1.

B. 2.

C. 3.

D. 4.

Câu 17: Tập nghiệm của phương trình \(\sqrt {3{x^2} - 6x - 4}  = \sqrt {x - 8} \) là

A. \(S = \left\{ {\frac{3}{4};1} \right\}\).

B. \(S = \left\{ {\frac{3}{4}} \right\}\).

C. \(S = \{ 1\} \).

D. \(S = \emptyset \).

Câu 18: Phương trình \(2{x^2} - 6x + 4 = 3\sqrt {{x^3} + 8} \) có hai nghiệm dạng \(x = a \pm b\sqrt {13} \) với \(a,b \in \mathbb{N}\). Tính \({a^2} - b\).

A. 0.

B. 1.

C. 8.

D. \( - 1\).

Câu 19: Trong mặt phẳng toạ độ \(Oxy\) cho các vectơ \(\vec a,\vec b,\vec c,\vec d\) được vẽ ở hình bên. Ta có các khẳng định sau:

 

A) \(\vec a = (2; - 3)\);

B) \(\vec b = ( - 3;0)\);

C) \(\vec c = (5;1)\);

D) \(\vec d = (4;0)\).

Số khẳng định đúng là:

A. 0.

B. 1.

C. 2.

D. 3.

Câu 20: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (2; - 3),\vec b = ( - 2;5)\). Toạ độ của vectơ \( - \vec a + 3\vec b\) là:

A. \((8;18)\).

B. \(( - 8; - 18)\).

C. \(( - 8;18)\).

D. \((8; - 18)\).

Câu 21: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (1;2),\vec b = (3; - 3)\). Toạ độ của vectơ \(\vec c = 3\vec a - 2\vec b\) là:

A. \(( - 3;12)\).

B. \((3;12)\).

C. \((9;0)\).

D. \(( - 3;0)\).

Câu 22: Trong mặt phẳng toạ độ \(Oxy\), cho hai điểm \(A(5;4),B( - 1;0)\). Đường trung trực của đoạn thẳng \(AB\) có phương trình là:

A. \(x - 2y + 5 = 0\).

B. \(3x + 2y - 10 = 0\).

C. \(3x + 2y - 5 = 0\).

D. \(2x + 3y - 1 = 0\).

Câu 23: Trong mặt phẳng tọ̣ độ \(Oxy\), cho ba điểm \(A(2;4),B(0; - 2),C(5;3)\). Đường thẳng đi qua điểm \(A\) và song song với đường thẳng \(BC\) có phương trình là:

A. \(x - y + 5 = 0\).

B. \(x + y - 5 = 0\).

C. \(x - y + 2 = 0\).

D. \(x + y = 0\).

Câu 24: Trong mặt phẳng toạ độ \(Oxy\), cho ba điểm \(A(5;2),B(5; - 2),C(4; - 3)\). Đường thẳng đi qua điểm \(A\) và vuông góc với đường thẳng \(BC\) có phương trình là:

A. \(x - y + 7 = 0\).

B. \(x + y - 7 = 0\).

C. \(x - y - 5 = 0\).

D. \(x + y = 0\).

Câu 25: Phương trình tổng quát của đường thẳng đi qua điểm \(A(1; - 3)\) và có vectơ pháp tuyến \(\vec n(2; - 1)\) là:

A. \(2x + y - 5 = 0\).

B. \(2x - y - 5 = 0\).

C. \(x + 2y + 5 = 0\).

D. \(x + 2y - 5 = 0\).

Câu 26: Phương trình tham số của đường thẳng đi qua điểm \(M(2;1)\) và có vectơ chỉ phương \(\vec u( - 1;4)\) là:

A. \(\left\{ {\begin{array}{*{20}{l}}{x = 2 + t}\\{y = 1 - 4t}\end{array}} \right.\).

B. \(\left\{ {\begin{array}{*{20}{l}}{x =  - 1 + 2t}\\{y = 4 + t}\end{array}} \right.\).

C. \(\left\{ {\begin{array}{*{20}{l}}{x = 1 + 4t}\\{y = 2 - t}\end{array}} \right.\).

D. \(\left\{ {\begin{array}{*{20}{l}}{x = 2 - t}\\{y = 1 + 4t}\end{array}} \right.\).

Câu 27: Phương trình đường thẳng đi qua hai điểm \(M( - 1;0),N(3;1)\) là:

A. \(x - 4y + 1 = 0\).

B. \(x - 4y - 1 = 0\).

C. \(4x + y + 4 = 0\).

D. \(4x + y - 4 = 0\).

Câu 28: Trong mặt phẳng toạ độ, cho đường thẳng \(d\): \(\left\{ {\begin{array}{*{20}{l}}{x =  - 1 - 2t}\\{y = 4 + 3t{\rm{. }}}\end{array}} \right.\) Vectơ chỉ phương của đường thẳng \(d\) là

A. \(\vec u = ( - 1;4)\).

B. \(\vec u = ( - 2;3)\).

C. \(\vec u = (3; - 2)\).

D. \(\vec u = (2;3)\).

Câu 29: Trong mặt phẳng toạ độ \(Oxy\), cho điểm \(M(2;4)\) và đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 5 + 3t}\\{y =  - 5 - 4t}\end{array}} \right.\). Khoảng cách từ \(M\) đến đường thẳng \(\Delta \) là:

A. \(\frac{5}{2}\).

B. 3.

C. 5.

D. \(\frac{9}{5}\).

Câu 30: Cho hai đường thẳng \({d_1}:3x - 4y + 5 = 0,{d_2}:4x - 3y + 2 = 0\). Điểm \(M\) nào sau đây cách đều hai đường thẳng trên?

A. \(M(1;0)\).

B. \(M(2;3)\).

C. \(M(4; - 2)\).

D. \(M( - 1;2)\).

Câu 31: Trong mặt phẳng toạ độ, cho đường thẳng \(\Delta :x - 2y - 3 = 0\). Đường thẳng nào sau đây có vị trí tương đối trùng với đường thẳng \(\Delta \)?

A. \({\Delta _1}:x + 2y - 3 = 0\).

B. \({\Delta _2}:2x + y - 3 = 0\).

C. \({\Delta _3}:2x - 4y - 1 = 0\).

D. \({\Delta _4}:2x - 4y - 6 = 0\).

Câu 32: Góc giữa hai đường thẳng \({\Delta _1}:\left\{ {\begin{array}{*{20}{c}}{x = 2 + t}\\{y =  - 1 + \sqrt 3 t}\end{array}} \right.\) và \({\Delta _2}:\left\{ {\begin{array}{*{20}{c}}{x = 3 - \sqrt 3 t}\\{y = 5 - t}\end{array}} \right.\) là

A. \({30^0}\).

B. \({45^0}\).

C. \({60^0}\).

D. \({90^0}\).

Câu 33: Đường tròn nào sau đây có tâm là \(I( - 3;5)\) và có bán kính là \(R = 4\)?

A. \({x^2} + {y^2} - 3x + 5y + 9 = 0\).

B. \({x^2} + {y^2} - 3x + 5y - 9 = 0\).

C. \({x^2} + {y^2} + 6x - 10y - 18 = 0\).

D. \({x^2} + {y^2} + 6x - 10y + 18 = 0\).

Câu 34: Phương trình đường tròn có tâm \(I(1;2)\) và đi qua điểm \(A( - 1;3)\) là:

A. \({(x + 1)^2} + {(y + 2)^2} = 25\).

B. \({(x + 1)^2} + {(y + 2)^2} = 5\).

C. \({(x - 1)^2} + {(y - 2)^2} = 5\).

D. \({(x - 1)^2} + {(y - 2)^2} = 25\).

Câu 35: Trong mặt phẳng toạ độ \(Oxy\), cho hai điểm \(A( - 4;6)\) và \(B( - 2;4)\). Phương trình đường tròn có đường kính \(AB\) là:

A. \({(x + 3)^2} + {(y - 5)^2} = 2\).

B. \({(x + 3)^2} + {(y + 5)^2} = 2\).

C. \({(x - 3)^2} + {(y + 5)^2} = 2\sqrt 2 \).

D. \({(x - 3)^2} + {(y - 5)^2} = 2\sqrt 2 \)

Phần tự luận (3 điểm)

Bài 1. Một vật chuyển động có vận tốc (mét/giây) được biểu diễn theo thời gian \(t\) (giây) bằng công thức \(v(t) = \frac{1}{2}{t^2} - 4t + 10\).

a) Hỏi sau tối thiểu bao nhiêu giây thì vận tốc của vật không bé hơn \(10\;m/s\) (biết rằng \(t > 0\))?

b) Trong 10 giây đầu tiên, vận tốc của vật đạt giá trị nhỏ nhất bằng bao nhiêu?

Bài 2. Giải phương trình sau: \(\sqrt {2{x^2} + 5}  = \sqrt {{x^2} - x + 11} \).

Bài 3. Cho các vectơ \(\vec a = (1; - 2),\vec b = ( - 2; - 6),\vec c = (m + n; - m - 4n)\).

a) Hai vectơ \(\vec a,\vec b\) có cùng phương không? Tìm góc tạo bởi hai vectơ \(\vec a,\vec b\).

b) Tìm hai số \(m,n\) sao cho \(\vec c\) cùng phương \(\vec a\) và \(|\vec c| = 3\sqrt 5 \).

Bài 4. Viết phương trình đường thẳng \(\Delta \) biết rằng:

a) \(\Delta \) chắn các trục tọa độ tại hai điểm \(A( - 4;0),B(0; - 2)\).

b) \(\Delta \) qua điểm \(E(2;3)\), đồng thời cắt các tia \(Ox,Oy\) tại các điểm \(M,N\) (khác gốc tọa độ \(O\)) biết rằng \(OM + ON\) bé nhất.

-------- Hết --------

Lời giải

Phần trắc nghiệm

 

Câu 1. D	Câu 2. C	Câu 3. A	Câu 4. D	Câu 5. A	Câu 6. A	Câu 7. D
Câu 8. D	Câu 9. D	Câu 10. A	Câu 11. D	Câu 12. B	Câu 13. B	Câu 14. A
Câu 15. B	Câu 16. D	Câu 17. D	Câu 18. C	Câu 19. C	Câu 20. C	Câu 21. A
Câu 22. B	Câu 23. C	Câu 24. B	Câu 25. B	Câu 26. D	Câu 27. A	Câu 28. B
Câu 29. B	Câu 30. B	Câu 31. D	Câu 32. A	Câu 33. D	Câu 34. C	Câu 35. A

 

Câu 1: Điều kiện để tam thức bậc hai \(a{x^2} + bx + c(a \ne 0)\) nhận giá trị âm với mọi \(x \in \mathbb{R}\) là:

A. \(\Delta  > 0\).

B. \(\Delta  < 0\).

C. \(\Delta  < 0\) và \(a > 0\).

D. \(\Delta  < 0\) và \(a < 0\).

Lời giải

Đáp án D.

Câu 2: Bảng xét dấu sau đây là của tam thức bậc hai nào?

A. \({x^2} - x + 6\).

B. \({x^2} + x + 6\).

C. \({x^2} - x - 6\).

D. \( - {x^2} + x - 6\).

Lời giải

Đáp án C.

Câu 3: Nghiệm của bất phương trình \({x^2} - 8x + 15 \le 0\) là:

A. \(x \in [3;5]\).

B. \(x \in (3;5)\).

C. \(x \in ( - \infty ;3] \cup [5; + \infty )\).

D. \(x \in ( - \infty ;3) \cup (5; + \infty )\).

Lời giải

Đáp án A.

Câu 4: Với giá trị nào của \(m\) thì bất phương trình \( - {x^2} - x + m \ge 0\) vô nghiệm?

A. \(m \ge  - \frac{1}{4}\).

B. \(m >  - \frac{1}{4}\).

C. \(m \le  - \frac{1}{4}\).

D. \(m <  - \frac{1}{4}\).

Lời giải

Đáp án D.

Câu 5: Một đường hầm xuyên thẳng qua núi và có mặt cắt là một parabol (thông số như hình bên). Giả sử một chiếc xe tải có chiều ngang \(6\;m\) đi vào vị trí chính giữa miệng hầm. Hỏi chiều cao \(h\) của xe tải cần thoả mãn điều kiện gì để có thể đi vào cửa hầm mà không chạm tường?

 

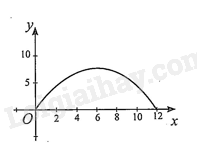
A. \(0 < h < 6\).

B. \(0 < h \le 6\).

C. \(0 < h < 7\).

D. \(0 < h \le 7\).

Lời giải

Chọn hệ trục toạ độ như hình bên.

Parabol có phương trình dạng \(y = a{x^2} + bx\). Theo đề bài ta có parabol đi qua các điểm \((12;0)\) và \((6;8)\). Suy ra \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}144a + 12b = 0\\36a + 6b = 8\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a =  - \frac{2}{9}\\b = \frac{8}{3}\end{array}\end{array}} \right.} \right.\)

Do đó \(y =  - \frac{2}{9}{x^2} + \frac{8}{3}x\). Do chiếc xe tải có chiều ngang \(6\;m\) đi vào vị trí chính giữa hầm nên xe sẽ chạm tường tại điểm \(A(3;6)\) và điểm \(B(9;6)\). Khi đó chiều cao của xe là \(6\;m\). Vậy điều kiện để xe tải có thể đi vào hầm mà không chạm tường là \(0 < h < 6\).

Đáp án A.

Câu 6: Giá trị nào của \(m\) thì phương trình \((m - 3){x^2} + (m + 3)x - (m + 1) = 0\) có hai nghiệm phân biệt?

A. \(m \in \left( { - \infty ; - \frac{3}{5}} \right) \cup (1; + \infty )\backslash \{ 3\} \).

B. \(m \in \left( { - \frac{3}{5};1} \right)\).

C. \(m \in \left( { - \frac{3}{5}; + \infty } \right)\).

D. \(m \in \mathbb{R}\backslash \{ 3\} \).

Lời giải

Phương trình đã cho có hai nghiệm phân biệt

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a \ne 0\\{\Delta ^\prime } > 0\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m - 3 \ne 0\\{(m + 3)^2} + 4(m - 3)(m + 1) > 0\end{array}\end{array}} \right.} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m \ne 3\\5{m^2} - 2m - 3 > 0\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m \ne 3\\m <  - \frac{3}{5} \vee m > 1\end{array}\end{array}} \right.} \right.\)

Đáp án A.

Câu 7: Tìm các giá trị của tham số \(m\) để bất phương trình \( - {x^2} + (2m - 1)x + m < 0\) có tập nghiệm là \(\mathbb{R}\).

A. \(m = \frac{1}{2}\).

B. \(m =  - \frac{1}{2}\).

C. \(m \in \mathbb{R}\).

D. Không tồn tại \(m\).

Lời giải

Bất phương trình \( - {x^2} + (2m - 1)x + m < 0\) có tập nghiệm là \(\mathbb{R}\) khi và chỉ khi:

Vậy không tồn tại \(m\) thỏa mãn đề bài.

Đáp án D.

Câu 8: Với giá trị nào của \(m\) thì bất phương trình \({x^2} - x + m \le 0\) vô nghiệm?

A. \(m < 1\).

B. \(m > 1\).

C. \(m < \frac{1}{4}\).

D. \(m > \frac{1}{4}\).

Lời giải

Ta có: \({x^2} - x + m \le 0\) vô nghiệm khi và chỉ khi \({x^2} - x + m > 0,\forall x \in \mathbb{R}\).

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a > 0\\\Delta  < 0\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}1 > 0{\rm{  }}\\1 - 4m < 0\end{array}\end{array} \Leftrightarrow m > \frac{1}{4}.} \right.} \right.\).

Đáp án D.

Câu 9: Bất phương trình \({x^2} - (m + 2)x + m + 2 \le 0\) vô nghiệm khi và chỉ khi:

A. \(m \in ( - \infty ; - 2] \cup [2; + \infty )\).

B. \(m \in ( - \infty ; - 2) \cup (2; + \infty )\).

C. \(m \in [ - 2;2]\).

D. \(m \in ( - 2;2)\).

Lời giải

Ta có: \({x^2} - (m + 2)x + m + 2 \le 0\) vô nghiệm khi và chỉ khi

\({x^2} - (m + 2)x + m + 2 > 0,\forall x \in \mathbb{R} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a > 0\\\Delta  < 0\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}1 > 0{\rm{  }}\\{m^2} - 4 < 0\end{array}\end{array} \Leftrightarrow  - 2 < m < 2.} \right.} \right.\)

Đáp án D.

Câu 10: Xác định \(m\) để với mọi \(x\), ta có \( - 1 \le \frac{{{x^2} + 5x + m}}{{2{x^2} - 3x + 2}} < 7\).

A. \( - \frac{5}{3} \le m < 1\).

B. \(1 < m \le \frac{5}{3}\).

C. \(m \le  - \frac{5}{3}\).

D. \(m < 1\).

Lời giải

Ta có \( - 1 \le \frac{{{x^2} + 5x + m}}{{2{x^2} - 3x + 2}} < 7,\forall x \in \mathbb{R}\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 1(2x - 3x + 2) \le {x^2} + 5x + m}\\{{x^2} + 5x + m < 7\left( {2{x^2} - 3x + 2} \right)}\end{array}} \right.\) có tập nghiệm \(\mathbb{R}\) (do \(\left. {2{x^2} - 3x + 2 > 0,\forall x \in \mathbb{R}} \right)\)

\( \Leftrightarrow \left\{ \begin{array}{l}3{x^2} + 2x + m + 2 \ge 0 &  & \left( 1 \right)\\13{x^2} - 26x + 14 - m > 0 & \left( 2 \right)\end{array} \right.\)có tập nghiệm\(\mathbb{R}\)

(1) có tập nghiệm là \(\mathbb{R} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{a_{(1)}} = 3 > 0}\\{\Delta _{(1)}^\prime  = {1^2} - 3(m + 2) \le 0}\end{array} \Leftrightarrow  - 5 - 3m \le 0} \right.\) \( \Leftrightarrow m \ge  - \frac{5}{3}\quad (3)\)

(2) có tập nghiệm là \(\mathbb{R} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{a_{(2)}} = 13 > 0}\\{\Delta _{(2)}^\prime  = {{( - 13)}^2} - 13(14 - m) < 0}\end{array}} \right.\) \( \Leftrightarrow  - 13 + 13m < 0 \Leftrightarrow m < 1\) (4).

Từ (3) và (4) suy ra: \( - \frac{5}{3} \le m < 1\) thỏa mãn đề bài.

Đáp án A.

Câu 11: Xác định \(m\) để \((x - 1)\left[ {{x^2} + 2(m + 3)x + 4m + 12} \right] = 0\) có ba nghiệm phân biệt lớn hơn \( - 1\).

A. \(m <  - \frac{7}{2}\)

B. \( - 2 < m < 1\) và \(m \ne  - \frac{{16}}{9}\).

C. \( - \frac{7}{2} < m <  - 1\) và \(m \ne  - \frac{{16}}{9}\).

D. \( - \frac{7}{2} < m <  - 3\) và \(m \ne  - \frac{{19}}{6}\).

Lời giải

Ta có: \((x - 1)\left[ {{x^2} + 2(m + 3)x + 4m + 12} \right] = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{{x^2} + 2(m + 3)x + 4m + 12 = 0\quad (*)}\end{array}} \right.\)

Yêu cầu bài toán tương đương \(\left( * \right)\) có hai nghiệm phân biệt \({x_1},{x_2}\) lớn hơn \( - 1\) và khác \(1(**)\).

Theo định li Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} =  - 2(m + 3)}\\{{x_1} \cdot {x_2} = 4m + 12}\end{array}} \right.\) (giả sử \(\left. {{x_1} < {x_2}} \right)\).

Do đó \(\left( {**} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\Delta ^\prime } > 0}\\{{1^2} + 2(m + 3) \cdot 1 + 4m + 12 \ne 0}\\{{x_2} > {x_1} >  - 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{{(m + 3)}^2} - (4m + 12) > 0}\\{6m + 19 \ne 0}\\{\left( {{x_1} + 1} \right) + \left( {{x_2} + 1} \right) > 0}\\{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) > 0}\end{array}} \right.} \right.\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{m^2} + 2m - 3 > 0\\m \ne  - \frac{{19}}{6}\\ - 2(m + 3) + 2 > 0\\4m + 12 - 2(m + 3) + 1 > 0\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m <  - 3 \vee m > 1\\m \ne  - \frac{{19}}{6}\\m <  - 2\\m >  - \frac{7}{2}\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l} - \frac{7}{2} < m <  - 3\\m \ne  - \frac{{19}}{6}\end{array}\end{array}} \right.} \right.} \right.\).

Đáp án D.

Câu 12: Tam thức bậc hai \(f(x) = {x^2} + (\sqrt 5  - 1)x - \sqrt 5 \) nhận giá trị dương khi?

A. \(x \in ( - \sqrt 5 ;1)\).

В. \(x \in ( - \infty ; - \sqrt 5 ) \cup (1; + \infty )\).

C. \(x \in ( - \sqrt 5 ; + \infty )\).

D. \(x \in ( - \infty ;1)\).

Lời giải

Ta có bảng xét dấu

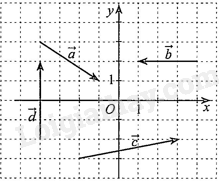
Đáp án B.

Câu 13: Cho phương trình \(\sqrt {{x^4} - 3{x^2} + 2}  = {x^2} + 2\). Nếu đặt \(t = {x^2},t \ge 0\) thì phương trình đã cho trở thành phương trình nào sau đây?

A. \(\sqrt {{t^2} - 3t + 2}  = {t^2} + 2\).

B. \(\sqrt {{t^2} - 3t + 2}  = t + 2\).

C. \(\sqrt {{t^2} - 3t + 2}  = t - 2\).

D. \(\sqrt {{t^2} + 3t - 2}  = t + 2\).

Lời giải

Đáp án B.

Câu 14: Số nghiệm của phương trình \(\sqrt {{x^2} - 4|x| + 3}  = 2x - 1\) là:

A. 1.

B. 2.

C. 4.

D. 0.

Lời giải

Đáp án A.

Câu 15: Tập nghiệm của phương trình \(\sqrt {{x^2} - 4x + 3}  = x + 1\) là:

A. \(S = \emptyset \).

B. \(S = \left\{ {\frac{1}{3}} \right\}\).

C. \(S = \{ 3\} \).

D. \(S = \{ 1\} \).

Lời giải

Đáp án B.

Câu 16: Số nghiệm của phương trình \(\sqrt {{x^2} - 3x + 2}  = \sqrt {2{x^2} - 7|x| + 4} \) là:

A. 1.

B. 2.

C. 3.

D. 4.

Lời giải

Đáp án D.

Câu 17: Tập nghiệm của phương trình \(\sqrt {3{x^2} - 6x - 4}  = \sqrt {x - 8} \) là

A. \(S = \left\{ {\frac{3}{4};1} \right\}\).

B. \(S = \left\{ {\frac{3}{4}} \right\}\).

C. \(S = \{ 1\} \).

D. \(S = \emptyset \).

Lời giải

Đáp án D.

Câu 18: Phương trình \(2{x^2} - 6x + 4 = 3\sqrt {{x^3} + 8} \) có hai nghiệm dạng \(x = a \pm b\sqrt {13} \) với \(a,b \in \mathbb{N}\). Tính \({a^2} - b\).

A. 0.

B. 1.

C. 8.

D. \( - 1\).

Lời giải

Điều kiện: \({x^3} + 8 \ge 0 \Leftrightarrow {x^3} \ge {( - 2)^3} \Leftrightarrow x \ge  - 2\).

Phương trình tương đương:

\(2\left( {{x^2} - 2x + 4} \right) - 2(x + 2) - 3\sqrt {(x + 2)\left( {{x^2} - 2x + 4} \right)}  = 0.\)

Chia hai vế phương trình cho \({x^2} - 2x + 4\) (với \({x^2} - 2x + 4 = {(x - 1)^2} + 3 \ne 0,\forall x \in \mathbb{R}\)), ta được: \(2 - 2\left( {\frac{{x + 2}}{{{x^2} - 2x + 4}}} \right) - 3\sqrt {\frac{{x + 2}}{{{x^2} - 2x + 4}}}  = 0\).

Đặt \(t = \sqrt {\frac{{x + 2}}{{{x^2} - 2x + 4}}} (t \ge 0)\).

Phương trình trở thành: \(2 - 2{t^2} - 3t = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = \frac{1}{2}{\rm{ (n) }}}\\{t =  - 2{\rm{ (l) }}}\end{array}} \right.\).

Với \(t = \frac{1}{2}\) thì \(\sqrt {\frac{{x + 2}}{{{x^2} - 2x + 4}}}  = \frac{1}{2} \Leftrightarrow 4(x + 2) = {x^2} - 2x + 4 \Leftrightarrow x = 3 \pm \sqrt {13} \) (nhận).

Do vậy: \(a = 3,b = 1 \Rightarrow {a^2} - b = 8\).

Đáp án C.

Câu 19: Trong mặt phẳng toạ độ \(Oxy\) cho các vectơ \(\vec a,\vec b,\vec c,\vec d\) được vẽ ở hình bên. Ta có các khẳng định sau:

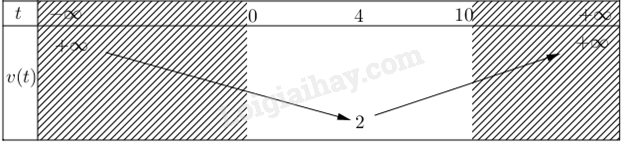
A) \(\vec a = (2; - 3)\); B) \(\vec b = ( - 3;0)\); C) \(\vec c = (5;1)\); D) \(\vec d = (4;0)\).

Số khẳng định đúng là:

A. 0.

B. 1.

C. 2.

D. 3.

Lời giải

Đáp án C.

Câu 20: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (2; - 3),\vec b = ( - 2;5)\). Toạ độ của vectơ \( - \vec a + 3\vec b\) là:

A. \((8;18)\).

B. \(( - 8; - 18)\).

C. \(( - 8;18)\).

D. \((8; - 18)\).

Lời giải

Ta có: \( - \vec a = ( - 2;3)\) và \(3\vec b = ( - 6;15)\). Suy ra \( - \vec a + 3\vec b = ( - 8;18)\).

Đáp án C.

Câu 21: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (1;2),\vec b = (3; - 3)\). Toạ độ của vectơ \(\vec c = 3\vec a - 2\vec b\) là:

A. \(( - 3;12)\).

B. \((3;12)\).

C. \((9;0)\).

D. \(( - 3;0)\).

Lời giải

Ta có: \(3\vec a = (3;6)\) và \( - 2\vec b = ( - 6;6)\). Suy ra \(3\vec a - 2\vec b = ( - 3;12)\).

Đáp án A.

Câu 22: Trong mặt phẳng toạ độ \(Oxy\), cho hai điểm \(A(5;4),B( - 1;0)\). Đường trung trực của đoạn thẳng \(AB\) có phương trình là:

A. \(x - 2y + 5 = 0\).

B. \(3x + 2y - 10 = 0\).

C. \(3x + 2y - 5 = 0\).

D. \(2x + 3y - 1 = 0\).

Lời giải

Đáp án B.

Câu 23: Trong mặt phẳng tọ̣ độ \(Oxy\), cho ba điểm \(A(2;4),B(0; - 2),C(5;3)\). Đường thẳng đi qua điểm \(A\) và song song với đường thẳng \(BC\) có phương trình là:

A. \(x - y + 5 = 0\).

B. \(x + y - 5 = 0\).

C. \(x - y + 2 = 0\).

D. \(x + y = 0\).

Lời giải

Đáp án C.

Câu 24: Trong mặt phẳng toạ độ \(Oxy\), cho ba điểm \(A(5;2),B(5; - 2),C(4; - 3)\). Đường thẳng đi qua điểm \(A\) và vuông góc với đường thẳng \(BC\) có phương trình là:

A. \(x - y + 7 = 0\).

B. \(x + y - 7 = 0\).

C. \(x - y - 5 = 0\).

D. \(x + y = 0\).

Lời giải

Đáp án B.

Câu 25: Phương trình tổng quát của đường thẳng đi qua điểm \(A(1; - 3)\) và có vectơ pháp tuyến \(\vec n(2; - 1)\) là:

A. \(2x + y - 5 = 0\).

B. \(2x - y - 5 = 0\).

C. \(x + 2y + 5 = 0\).

D. \(x + 2y - 5 = 0\).

Lời giải

Đáp án B.

Câu 26: Phương trình tham số của đường thẳng đi qua điểm \(M(2;1)\) và có vectơ chỉ phương \(\vec u( - 1;4)\) là:

A. \(\left\{ {\begin{array}{*{20}{l}}{x = 2 + t}\\{y = 1 - 4t}\end{array}} \right.\).

B. \(\left\{ {\begin{array}{*{20}{l}}{x =  - 1 + 2t}\\{y = 4 + t}\end{array}} \right.\).

C. \(\left\{ {\begin{array}{*{20}{l}}{x = 1 + 4t}\\{y = 2 - t}\end{array}} \right.\).

D. \(\left\{ {\begin{array}{*{20}{l}}{x = 2 - t}\\{y = 1 + 4t}\end{array}} \right.\).

Lời giải

Đáp án D.

Câu 27: Phương trình đường thẳng đi qua hai điểm \(M( - 1;0),N(3;1)\) là:

A. \(x - 4y + 1 = 0\).

B. \(x - 4y - 1 = 0\).

C. \(4x + y + 4 = 0\).

D. \(4x + y - 4 = 0\).

Lời giải

Đáp án A.

Câu 28: Trong mặt phẳng toạ độ, cho đường thẳng \(d\): \(\left\{ {\begin{array}{*{20}{l}}{x =  - 1 - 2t}\\{y = 4 + 3t{\rm{. }}}\end{array}} \right.\) Vectơ chỉ phương của đường thẳng \(d\) là

A. \(\vec u = ( - 1;4)\).

B. \(\vec u = ( - 2;3)\).

C. \(\vec u = (3; - 2)\).

D. \(\vec u = (2;3)\).

Lời giải

Đáp án B.

Câu 29: Trong mặt phẳng toạ độ \(Oxy\), cho điểm \(M(2;4)\) và đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 5 + 3t}\\{y =  - 5 - 4t}\end{array}} \right.\). Khoảng cách từ \(M\) đến đường thẳng \(\Delta \) là:

A. \(\frac{5}{2}\).

B. 3.

C. 5.

D. \(\frac{9}{5}\).

Lời giải

Đáp án B.

Câu 30: Cho hai đường thẳng \({d_1}:3x - 4y + 5 = 0,{d_2}:4x - 3y + 2 = 0\). Điểm \(M\) nào sau đây cách đều hai đường thẳng trên?

A. \(M(1;0)\).

B. \(M(2;3)\).

C. \(M(4; - 2)\).

D. \(M( - 1;2)\).

Lời giải

Đáp án B.

Câu 31: Trong mặt phẳng toạ độ, cho đường thẳng \(\Delta :x - 2y - 3 = 0\). Đường thẳng nào sau đây có vị trí tương đối trùng với đường thẳng \(\Delta \)?

A. \({\Delta _1}:x + 2y - 3 = 0\).

B. \({\Delta _2}:2x + y - 3 = 0\).

C. \({\Delta _3}:2x - 4y - 1 = 0\).

D. \({\Delta _4}:2x - 4y - 6 = 0\).

Lời giải

Đáp án D.

Câu 32: Góc giữa hai đường thẳng \({\Delta _1}:\left\{ {\begin{array}{*{20}{c}}{x = 2 + t}\\{y =  - 1 + \sqrt 3 t}\end{array}} \right.\) và \({\Delta _2}:\left\{ {\begin{array}{*{20}{c}}{x = 3 - \sqrt 3 t}\\{y = 5 - t}\end{array}} \right.\) là

A. \({30^0}\).

B. \({45^0}\).

C. \({60^0}\).

D. \({90^0}\).

Lời giải

Đáp án A.

Câu 33: Đường tròn nào sau đây có tâm là \(I( - 3;5)\) và có bán kính là \(R = 4\)?

A. \({x^2} + {y^2} - 3x + 5y + 9 = 0\).

B. \({x^2} + {y^2} - 3x + 5y - 9 = 0\).

C. \({x^2} + {y^2} + 6x - 10y - 18 = 0\).

D. \({x^2} + {y^2} + 6x - 10y + 18 = 0\).

Lời giải

Đáp án D.

Câu 34: Phương trình đường tròn có tâm \(I(1;2)\) và đi qua điểm \(A( - 1;3)\) là:

A. \({(x + 1)^2} + {(y + 2)^2} = 25\).

B. \({(x + 1)^2} + {(y + 2)^2} = 5\).

C. \({(x - 1)^2} + {(y - 2)^2} = 5\).

D. \({(x - 1)^2} + {(y - 2)^2} = 25\).

Lời giải

Đáp án C.

Câu 35: Trong mặt phẳng toạ độ \(Oxy\), cho hai điểm \(A( - 4;6)\) và \(B( - 2;4)\). Phương trình đường tròn có đường kính \(AB\) là:

A. \({(x + 3)^2} + {(y - 5)^2} = 2\).

B. \({(x + 3)^2} + {(y + 5)^2} = 2\).

C. \({(x - 3)^2} + {(y + 5)^2} = 2\sqrt 2 \).

D. \({(x - 3)^2} + {(y - 5)^2} = 2\sqrt 2 \)

Lời giải

Đáp án A.

Phần tự luận (3 điểm)

Bài 1. Một vật chuyển động có vận tốc (mét/giây) được biểu diễn theo thời gian \(t\) (giây) bằng công thức \(v(t) = \frac{1}{2}{t^2} - 4t + 10\).

a) Hỏi sau tối thiểu bao nhiêu giây thì vận tốc của vật không bé hơn \(10\;m/s\) (biết rằng \(t > 0\))?

b) Trong 10 giây đầu tiên, vận tốc của vật đạt giá trị nhỏ nhất bằng bao nhiêu?

Lời giải

a) Để vận tốc vật không dưới \(10\;m/s\), ta cần xét:

\(v(t) = \frac{1}{2}{t^2} - 4t + 10 \ge 10 \Rightarrow \frac{1}{2}{t^2} - 4t \ge 0.\)

Xét \(f(t) = \frac{1}{2}{t^2} - 4t;f(t) = 0 \Leftrightarrow \frac{1}{2}{t^2} - 4t = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = 0}\\{t = 8}\end{array}} \right.\).

Bảng xét dấu \(f(t)\):

Ta có: \(f(t) \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t \le 0{\rm{ (}}l{\rm{) }}}\\{t \ge 8}\end{array}} \right.\).

Vậy, thời gian tối thiểu là 8 giây thì vật sẽ đạt vận tốc không bé hơn \(10\;m/s\).

b) Xét \(v(t) = \frac{1}{2}{t^2} - 4t + 10\) với \( - \frac{b}{{2a}} = 4,a = \frac{1}{2} > 0\) nên bề lõm parabol hướng lên. Bảng biến thiên của \(v(t)\):

Vậy, ở giây thứ tư thì vận tốc của vật đạt giá trị nhỏ nhất là \(v{(t)_{\min }} = 2\).

Bài 2. Giải phương trình sau: \(\sqrt {2{x^2} + 5}  = \sqrt {{x^2} - x + 11} \).

Lời giải

Cách 1:

Bình phương hai vế phương trình, ta được:

\(2{x^2} + 5 = {x^2} - x + 11 \Leftrightarrow {x^2} + x - 6 = 0 \Leftrightarrow x = 2 \vee x =  - 3.{\rm{ }}\)

Thay giá trị \(x = 2\) vào phương trình: \(\sqrt {13}  = \sqrt {13} \) (thỏa mãn).

Thay giá trị \(x =  - 3\) vào phương trình: \(\sqrt {23}  = \sqrt {23} \) (thỏa mãn).

Vậy tập nghiệm phương trình là \(S = \{ 2; - 3\} \).

Cách 2:

Ta có: \(\sqrt {2{x^2} + 5}  = \sqrt {{x^2} - x + 11}  \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2{x^2} + 5 \ge 0,\forall x \in \mathbb{R}}\\{2{x^2} + 5 = {x^2} - x + 11}\end{array} \Leftrightarrow {x^2} + x - 6 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2}\\{x =  - 3}\end{array}} \right.} \right.\).

Vậy tập nghiệm phương trình là \(S = \{ 2; - 3\} \).

Bài 3. Cho các vectơ \(\vec a = (1; - 2),\vec b = ( - 2; - 6),\vec c = (m + n; - m - 4n)\).

a) Hai vectơ \(\vec a,\vec b\) có cùng phương không? Tìm góc tạo bởi hai vectơ \(\vec a,\vec b\).

b) Tìm hai số \(m,n\) sao cho \(\vec c\) cùng phương \(\vec a\) và \(|\vec c| = 3\sqrt 5 \).

Lời giải

a) Ta có: \(\frac{1}{{ - 2}} \ne \frac{{ - 2}}{{ - 6}} \Rightarrow \vec a,\vec b\) không cùng phương.

Ta có: \(\cos (\vec a,\vec b) = \frac{{\vec a \cdot \vec b}}{{|\vec a| \cdot |\vec b|}} = \frac{{1( - 2) + ( - 2)( - 6)}}{{\sqrt {{1^2} + {{( - 2)}^2}}  \cdot \sqrt {{{( - 2)}^2} + {{( - 6)}^2}} }} = \frac{{\sqrt 2 }}{2} \Rightarrow (\vec a,\vec b) = 45^\circ \).

b) \(\vec c\) cùng phương \(\vec a\) và \(|\vec c| = 3\sqrt 5  \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{{m + n}}{1} = \frac{{ - m - 4n}}{{ - 2}}}\\{\sqrt {{{(m + n)}^2} + {{( - m - 4n)}^2}}  = 3\sqrt 5 }\end{array}} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l} - 2m - 2n =  - m - 4n\\{(m + n)^2} + {(m + 4n)^2} = 45\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m = 2n\\{(3n)^2} + {(6n)^2} = 45\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m = 2n\\{(3n)^2} + {(6n)^2} = 45\end{array}\end{array}} \right.} \right.} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m = 2n\\45{n^2} = 45\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m = 2\\n = 1\end{array}\end{array} \vee \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m =  - 2\\n =  - 1\end{array}\end{array}.} \right.} \right.} \right.\end{array}\)

Bài 4. Viết phương trình đường thẳng \(\Delta \) biết rằng:

a) \(\Delta \) chắn các trục tọa độ tại hai điểm \(A( - 4;0),B(0; - 2)\).

b) \(\Delta \) qua điểm \(E(2;3)\), đồng thời cắt các tia \(Ox,Oy\) tại các điểm \(M,N\) (khác gốc tọa độ \(O\)) biết rằng \(OM + ON\) bé nhất.

Lời giải

a) \(\Delta \) có phương trình theo đoạn chắn là \(\frac{x}{{ - 4}} + \frac{y}{{ - 2}} = 1\) hay \(x + 2y + 4 = 0\).

b) Gọi \(M(m;0) = \Delta  \cap Ox,N(0;n) = \Delta  \cap Oy\) với \(m,n > 0\). Suy ra \(\left\{ {\begin{array}{*{20}{l}}{OM = m}\\{ON = n}\end{array}} \right.\).

Phương trình \(\Delta \) được viết theo đoạn chắn \(\frac{x}{m} + \frac{y}{n} = 1\). Vì \(E(2;3) \in \Delta \) nên \(\frac{2}{m} + \frac{3}{n} = 1 \Rightarrow \frac{2}{m} = \frac{{n - 3}}{n} \Rightarrow m = \frac{{2n}}{{n - 3}}\). Vì \(m,n > 0\) nên \(n - 3 > 0 \Rightarrow n > 3\).

Ta có: \(OM + ON = m + n = \frac{{2n}}{{n - 3}} + n = 2 + \frac{6}{{n - 3}} + n = 5 + \frac{6}{{n - 3}} + (n - 3)\).

Áp dụng bất đẳng thức AM-GM: \(\frac{6}{{n - 3}} + (n - 3) \ge 2\sqrt {\frac{6}{{n - 3}} \cdot (n - 3)}  = 2\sqrt 6 \).

Suy ra: \(OM + ON = 5 + \frac{6}{{n - 3}} + (n - 3) \ge 5 + 2\sqrt 6 \).

Khi tổng \(OM + ON\) đạt giá trị nhỏ nhất (bằng \(5 + 2\sqrt 6 \)) thì dấu bằng của bất đẳng thức trên xảy ra: \(\frac{6}{{n - 3}} = n - 3 \Rightarrow {(n - 3)^2} = 6 \Rightarrow n = \sqrt 6  + 3(n > 3)\). Suy ra \(m = \frac{{2(\sqrt 6  + 3)}}{{(\sqrt 6  + 3) - 3}} = \frac{{2\sqrt 6  + 6}}{{\sqrt 6 }} = 2 + \sqrt 6 \).

Phương trình tổng quát \(\Delta :\frac{x}{{2 + \sqrt 6 }} + \frac{y}{{3 + \sqrt 6 }} = 1\) hay \(\frac{x}{{2 + \sqrt 6 }} + \frac{y}{{3 + \sqrt 6 }} - 1 = 0\).