Đề thi giữa kì 1 Toán 10 Chân trời sáng tạo - Đề số 10Tải về Phần trắc nghiệm (7 điểm) Câu 1: Câu nào sau đây không là mệnh đề chứa biến? A. (x + 1 > 0) B. x chia hết cho 2 C. (5 - 6 > 1) D. (left( {7 - x} right)left( {7 + x} right) = 49 - {x^2}) Đề bài Phần trắc nghiệm (7 điểm) Câu 1: Câu nào sau đây không là mệnh đề chứa biến?
Câu 2: Trong các câu sau, câu nào dùng được kí hiệu “∃” để viết thành câu mà nội dung câu không đổi:
Câu 3: Chọn câu đúng nhất.
Câu 4: Tập hợp nào sau đây viết dưới dạng liệt kê các phần tử?
Câu 5: Chọn đáp án đúng nhất: Tập hợp nào dưới đây viết dưới dạng chỉ ra tính chất đặc trưng cho phần tử?
Câu 6: Tập hợp A gồm các số tự nhiên chia hết cho 5 và nhỏ hơn 30. Cách viết nào sau đây đúng?
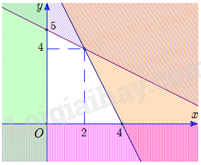
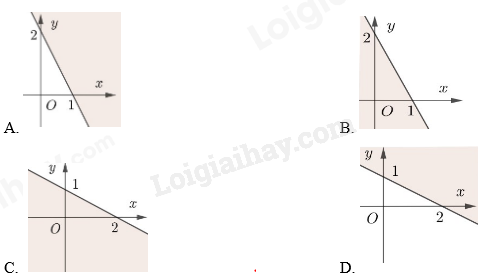
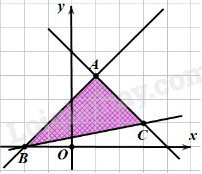
Câu 7: Miền nghiệm của một hệ bất phương trình là miền không bị gạch chéo (tính cả bờ) như hình dưới. Điểm nào sau đây không nằm trong miền nghiệm của hệ bất phương trình trên?
Câu 8: Hệ nào dưới đây là hệ bất phương trình bậc nhất hai ẩn?
Câu 9: Hệ bất phương trình {6x−2y>1x−4y<6 có tập nghiệm là S. Khẳng định nào sau đây đúng?
Câu 10: Miền nghiệm của bất phương trình 4x+10y−5>0 là:
Câu 11: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
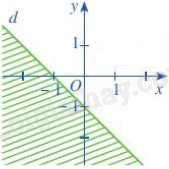
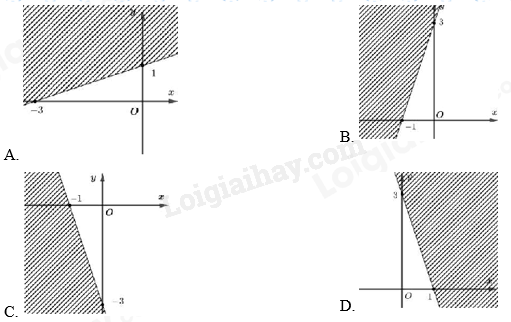
Câu 12: Cho bất phương trình có miền nghiệm là phần không bị gạch chéo (tính cả bờ) như hình dưới. Điểm nào sau đây không nằm trong miền nghiệm của bất phương trình trên?
Câu 13: Với 00≤α≤1800 và α=1800−β thì:
Câu 14: Chọn đáp án đúng.
Câu 15: Chọn đáp án đúng
Câu 16: Cho tam giác ABC nhọn. Chọn đáp án đúng nhất.
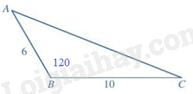
Câu 17: Cho hình vẽ: Chọn đáp án đúng.
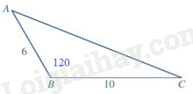
Câu 18: Cho tam giác ABC có ˆA=450,ˆB=600. Chọn đáp án đúng.
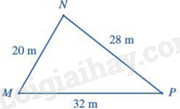
Câu 19: Tính diện tích tam giác MNP có hình vẽ như dưới đây (làm tròn kết quả đến hàng phần trăm):
Câu 20: Cho tam giác ABC vuông tại tại A có AB=6cm,AC=8cm thì diện tích tam giác ABC là:
Câu 21: Câu nào sau đây là mệnh đề sai?
Câu 22: Xét hai mệnh đề: P: “Tứ giác ABCD là hình bình hành” Q: “Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường”. Chọn đáp án đúng nhất.
Câu 23: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Trời nóng quá!, b) Việt Nam nằm ở khu vực Nam Á, c) 10−2+5>8, d) Năm 2023 là năm nhuận, e) Hôm nay là thứ mấy?
Câu 24: Cho tập hợp A={x∈R|x2−9=0}. Chọn đáp án đúng.
Câu 25: Trong các khẳng định sau, khẳng định nào đúng?
Câu 26: Trong các tập hợp sau, tập hợp nào khác rỗng?
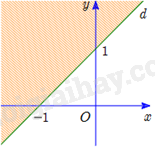
Câu 27: Miền nghiệm của bất phương trình 2x+y>2 là miền không tô màu trong hình vẽ nào sau đây? Câu 28: Miền nghiệm của bất phương trình 3x+y<3 được biểu diễn bởi phần không gạch chéo trong hình nào dưới đây? Câu 29: Bất phương trình nào sau đây có miền nghiệm được biểu diễn bởi phần không gạch sọc (tính cả bờ) trong hình vẽ dưới đây?
Câu 30: Cho hệ bất phương trình {x−y≥−2x+y≤4x−5y≤−2. Giá trị lớn nhất của biểu thức F=−x+2y trên miền nghiệm của hệ bất phương trình
Câu 31: Cho tam giác ABC. Chọn khẳng định đúng.
Câu 32: Tính B=cos150+cos350−sin750−sin550
Câu 33: Cho tam giác ABC có AB=c,BC=a,AC=b. Biết rằng a2=b2+c2+√2bc. Tính số đo góc A.
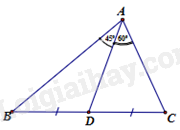
Câu 34: Cho hình vẽ dưới đây. Chọn đáp án đúng
Câu 35: Cho tam giác ABC có AB=3cm,BC=5cm,CA=6cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Phần tự luận (3 điểm) Bài 1. (1,0 điểm) Thống kê tại một trung tâm mua sắm gồm 24 cửa hàng bán quần áo, 14 cửa hàng có bán giày và 30 cửa hàng bán ít nhất một trong hai mặt hàng này. Hỏi có bao nhiêu cửa hàng bán cả giày và quần áo? Bài 2. (1,0 điểm)
Bài 3. (1,0 điểm) Cho tam giác ABC, chứng minh nếu cos2A+cos2Bsin2A+sin2B=12(cot2A+cot2B) thì tam giác ABC là tam giác cân.
-------- Hết -------- Lời giải chi tiết Phần trắc nghiệm (7 điểm)
Câu 1: Câu nào sau đây không là mệnh đề chứa biến?
Phương pháp Sử dụng kiến thức về mệnh đề chứa biến. Lời giải Câu “5−6>1” không phải là mệnh đề chứa biến. Đáp án C Câu 2: Trong các câu sau, câu nào dùng được kí hiệu “∃” để viết thành câu mà nội dung câu không đổi:
Phương pháp Kí hiệu ∃ đọc là “tồn tại” Lời giải Câu có sử dụng kí hiệu “∃” để viết lại câu là: Tồn tại một số tự nhiên mà bình phương của nó bằng 4 Đáp án B Câu 3: Chọn câu đúng nhất.
Phương pháp Mệnh đề “∀x∈M,P(x)” đúng nếu với mọi xo∈M, P(xo) là mệnh đề đúng. Mệnh đề “∃x∈M,P(x)” đúng nếu có xo∈M sao cho P(xo) là mệnh đề đúng Lời giải Câu đúng: Mệnh đề “∀x∈M,P(x)” đúng nếu với mọi xo∈M, P(xo) là mệnh đề đúng. Mệnh đề “∃x∈M,P(x)” đúng nếu có xo∈M sao cho P(xo) là mệnh đề đúng. Đáp án D Câu 4: Tập hợp nào sau đây viết dưới dạng liệt kê các phần tử?
Phương pháp Sử dụng kiến thức về viết tập hợp bằng cách chỉ ra tính chất đặc trưng của các phần tử của tập hợp. Lời giải Cách viết tập hợp dưới dạng liệt kê các phần tử của tập hợp là: N={m;n;p;q} Đáp án B Câu 5: Chọn đáp án đúng nhất: Tập hợp nào dưới đây viết dưới dạng chỉ ra tính chất đặc trưng cho phần tử?
Phương pháp Sử dụng kiến thức về viết tập hợp bằng cách chỉ ra tính chất đặc trưng của các phần tử của tập hợp. Lời giải Đáp án đúng: A={x| x là số tự nhiên, x chẵn, x<7}; A={x∈N|x⋮2,x<7} Đáp án C Câu 6: Tập hợp A gồm các số tự nhiên chia hết cho 5 và nhỏ hơn 30. Cách viết nào sau đây đúng?
Phương pháp - Khi liệt kê các phần tử của tập hợp, ta cần chú ý 1 số chú ý: + Các phần tử của tập hợp cho vào trong dấu ngoặc {}. + Các phần tử có thể viết theo thứ tự tùy ý. + Mỗi phần tử chỉ liệt kê một lần. + Nếu quy tắc các phần tử đủ rõ thì người ta dùng “…” mà không nhất thiết viết ra tất cả các phần tử của tập hợp. - Sử dụng kiến thức về viết tập hợp bằng cách chỉ ra tính chất đặc trưng của các phần tử của tập hợp. Lời giải Cách viết đúng: A={0;5;10;15;20;25} Đáp án A Câu 7: Miền nghiệm của một hệ bất phương trình là miền không bị gạch chéo (tính cả bờ) như hình dưới. Điểm nào sau đây không nằm trong miền nghiệm của hệ bất phương trình trên?
Phương pháp Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ Oxy, ta thực hiện: + Trên cùng mặt phẳng tọa độ, biểu diễn miền nghiệm của mỗi bất phương trình của hệ. + Phần giao của các miền nghiệm là nghiệm của hệ bất phương trình. Lời giải Trong các điểm trên, chỉ có điểm (0;−3) thuộc miền bị gạch chéo trong mặt phẳng tọa độ. Vậy điểm (0;−3) không nằm trong miền nghiệm của hệ bất phương trình đã cho. Đáp án B Câu 8: Hệ nào dưới đây là hệ bất phương trình bậc nhất hai ẩn?
Phương pháp Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn x, y Lời giải Hệ bất phương trình bậc nhất hai ẩn là {x≥9y≥02x−4y≤0 Đáp án D Câu 9: Hệ bất phương trình {6x−2y>1x−4y<6 có tập nghiệm là S. Khẳng định nào sau đây đúng?
Phương pháp Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn x, y. Mỗi nghiệm chung của các bất phương trình trong hệ được gọi là một nghiệm của hệ bất phương trình đó. Lời giải Với x=1;y=12 ta có: {6.1−2.12>11−4.12<6 nên (1;12)∈S Với x=−1;y=1 ta có: (−1).6−2.1<1 nên (−1;1)∉S Với x=3;y=−2 ta có: 3+4.2>6 nên (3;−2)∉S Với x=1;y=−2 ta có: 1+4.2>6 nên (1;−2)∉S Đáp án C Câu 10: Miền nghiệm của bất phương trình 4x+10y−5>0 là:
Phương pháp Biểu diễn miền nghiệm của bất phương trình ax+by+c>0 như sau: Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng d:ax+by+c=0 Bước 2: Lấy một điểm (x0;y0) không thuộc d. Tính ax0+by0+c Bước 3: Kết luận: + Nếu ax0+by0+c>0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) chứa điểm (x0;y0) + Nếu ax0+by0+c<0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) không chứa điểm (x0;y0) Lời giải Ta thấy điểm O (0; 0) không thuộc đường thẳng d:4x+10y−5=0 và 4.0+10.0−5<0 nên điểm O không thuộc miền nghiệm của bất phương trình 4x+10y−5>0. Vậy miền nghiệm của bất phương trình 4x+10y−5>0 là nửa mặt phẳng không kể bờ d không chứa điểm O (0; 0) Đáp án D Câu 11: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
Phương pháp Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng ax+by+c>0,ax+by+c≥0,ax+by+c<0,ax+by+c≤0 Trong đó a, b, c là những số cho trước, a, b không đồng thời bằng 0 và x, y là các ẩn. Lời giải Bất phương trình bậc nhất hai ẩn là x4+y5≥8 Đáp án C Câu 12: Cho bất phương trình có miền nghiệm là phần không bị gạch chéo (tính cả bờ) như hình dưới. Điểm nào sau đây không nằm trong miền nghiệm của bất phương trình trên?
Phương pháp Trong mặt phẳng tọa độ Oxy, tập hợp các điểm (x0;y0) sao cho khi thay các giá trị x0;y0 vào bất phương trình bậc nhất hai ẩn luôn được bất phương trình đúng được gọi là miền nghiệm của bất phương trình đó. Lời giải Trong các điểm ở trên, chỉ có điểm (0;−4) thuộc miền bị gạch chéo. Do đó, điểm (0;−4) không nằm trong miền nghiệm của bất phương trình. Đáp án B Câu 13: Với 00≤α≤1800 và α=1800−β thì:
Phương pháp Với 00≤α≤1800 thì sin(1800−α)=sinα Lời giải Ta có: sinβ=sin(1800−β)=sinα Đáp án A Câu 14: Chọn đáp án đúng.
Phương pháp cot300=√3 Lời giải cot300=√3 Đáp án C Câu 15: Chọn đáp án đúng
Phương pháp sin450=√22;cos450=√22 Lời giải Vì sin450=√22;cos450=√22 nên sin450=cos450 Đáp án A Câu 16: Cho tam giác ABC nhọn. Chọn đáp án đúng nhất.
Phương pháp Nếu α là góc nhọn thì, sinα>0 Lời giải Tam giác ABC nhọn nên góc A, B, C là các góc nhọn. Do đó, sinA>0, sinB>0, sinC>0 Đáp án D Câu 17: Cho hình vẽ: Chọn đáp án đúng.
Phương pháp Định lý côsin: Cho tam giác ABC có AB=c,BC=a,AC=b thì b2=a2+c2−2accosB Lời giải Theo định lí cosin ta có: AC2=AB2+BC2−2.AB.BC.cosB=62+102−2.6.10cos1200=196⇒AC=14 Đáp án B Câu 18: Cho tam giác ABC có ˆA=450,ˆB=600. Chọn đáp án đúng.
Phương pháp Định lí sin: Cho tam giác ABC có AB=c,BC=a,AC=b. Khi đó, asinA=bsinB=csinC Lời giải Áp dụng định lí sin vào tam giác ABC ta có: BCsinA=ACsinB Do đó, BCAC=sinAsinB=sin450sin600=√22√32=√63 Đáp án C Câu 19: Tính diện tích tam giác MNP có hình vẽ như dưới đây (làm tròn kết quả đến hàng phần trăm):
Phương pháp Cho tam giác ABC có AB=c,BC=a,AC=b, p là nửa chu vi tam giác ABC thì diện tích S của tam giác ABC là: S=√p(p−a)(p−b)(p−c) Lời giải Nửa chu vi tam giác là: p=20+28+322=40(m) Diện tích tam giác MNP là: SMNP=√40(40−20)(40−28)(40−32)≈277,13(m2) Đáp án C Câu 20: Cho tam giác ABC vuông tại tại A có AB=6cm,AC=8cm thì diện tích tam giác ABC là:
Phương pháp Cho tam giác có độ dài 1 cạnh bằng a, độ dài đường cao ứng với cạnh đó là ha thì diện tích tam giác là: S=12a.ha Lời giải Diện tích tam giác ABC là: S=12AB.AC=12.6.8=24(cm2) Đáp án D Câu 21: Câu nào sau đây là mệnh đề sai?
Phương pháp Một khẳng định đúng gọi là mệnh đề đúng, khẳng định sai gọi là mệnh đề sai. Lời giải Mệnh đề sai là: Hình bình hành có hai đường chéo vuông góc là hình chữ nhật Đáp án C Câu 22: Xét hai mệnh đề: P: “Tứ giác ABCD là hình bình hành” Q: “Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường”. Chọn đáp án đúng nhất
Phương pháp Mệnh đề “Q⇒P” được gọi là mệnh đề đảo của mệnh đề “P⇒Q” Lời giải Mệnh đề P⇒Q là: Nếu tứ giác ABCD là hình bình hành thì tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường. Đây là mệnh đề đúng. Mệnh đề đảo của mệnh đề P⇒Q là: Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành. Đây là mệnh đề đúng. Đáp án D Câu 23: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Trời nóng quá!, b) Việt Nam nằm ở khu vực Nam Á, c) 10−2+5>8, d) Năm 2023 là năm nhuận, e) Hôm nay là thứ mấy?
Phương pháp Mệnh đề là một câu khẳng định đúng hoặc sai Lời giải Các câu là mệnh đề là: b, c, d Đáp án C Câu 24: Cho tập hợp A={x∈R|x2−9=0}. Chọn đáp án đúng.
Phương pháp Nếu tất cả những phần tử của tập A đều thuộc tập B thì ta nói A là tập con của B, kí hiệu A⊂B Lời giải Vì x2−9=0 nên x=±3. Do đó, 3∈A, A={3;−3}, {−3}⊂A. Vậy câu sai là: {3}∈A Đáp án D Câu 25: Trong các khẳng định sau, khẳng định nào đúng?
Phương pháp Tập hợp gồm những phần tử thuộc tập hợp A hoặc thuộc tập hợp B được gọi là hợp của A và B, kí hiệu A∪B. Tập hợp gồm những phần tử vừa thuộc A vừa thuộc B được gọi là giao của A và B, kí hiệu là A∩B. Tập hợp gồm những phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B, kí hiệu A∖B Lời giải Đáp án đúng: N∗∩Q=N∗ Đáp án B Câu 26: Trong các tập hợp sau, tập hợp nào khác rỗng?
Phương pháp Tập hợp không chứa phần tử nào được gọi là tập rỗng, kí hiệu ∅ Lời giải Vì x(x2+3)=0 nên x=0. Do đó, A={0} nên tập hợp A khác rỗng. Vì x2−3=0 nên x=±√3, mà x∈N nên B=∅ Vì x2+3>0∀x∈R nên C=∅ Vì (x2−2)(x2+5)=0 nên x=±√2, mà x∈Z nên D=∅ Đáp án A Câu 27: Miền nghiệm của bất phương trình 2x+y>2 là miền không tô màu trong hình vẽ nào sau đây? Phương pháp Biểu diễn miền nghiệm của bất phương trình ax+by+c>0 như sau: Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng d:ax+by+c=0 Bước 2: Lấy một điểm (x0;y0) không thuộc d. Tính ax0+by0+c Bước 3: Kết luận: + Nếu ax0+by0+c>0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) chứa điểm (x0;y0) + Nếu ax0+by0+c<0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không tính bờ d) không chứa điểm (x0;y0) Lời giải Ta thấy điểm O (0; 0) không thuộc đường thẳng d:2x+y−2=0 và 2.0+0<2 nên miền nghiệm của bất phương trình 2x+y>2 là nửa mặt phẳng (không kể bờ d) không chứa điểm O. Đáp án B Câu 28: Miền nghiệm của bất phương trình 3x+y<3 được biểu diễn bởi phần không gạch chéo trong hình nào dưới đây? Phương pháp Biểu diễn miền nghiệm của bất phương trình ax+by+c<0 như sau: Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng d:ax+by+c=0 Bước 2: Lấy một điểm (x0;y0) không thuộc d. Tính ax0+by0+c Bước 3: Kết luận: + Nếu ax0+by0+c<0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) chứa điểm (x0;y0) + Nếu ax0+by0+c>0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) không chứa điểm (x0;y0) Lời giải Nhận thấy, điểm O (0; 0) không thuộc đường thẳng d:3x+y−3=0 và 3.0+0<3 nên miền nghiệm của bất phương trình 3x+y<3 là nửa mặt phẳng bờ là đường thẳng d (không tính bờ) chứa điểm O. Đáp án D Câu 29: Bất phương trình nào sau đây có miền nghiệm được biểu diễn bởi phần không gạch sọc (tính cả bờ) trong hình vẽ dưới đây?
Phương pháp Biểu diễn miền nghiệm của bất phương trình ax+by+c>0 như sau: Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng d:ax+by+c=0 Bước 2: Lấy một điểm (x0;y0) không thuộc d. Tính ax0+by0+c Bước 3: Kết luận: + Nếu ax0+by0+c<0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) không chứa điểm (x0;y0) + Nếu ax0+by0+c>0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) chứa điểm (x0;y0) Lời giải Đường thẳng d có phương trình là: −x+y−1=0 Ta thấy điểm O (0; 0) không thuộc đường thẳng d, −0+0−1≤0 và O thuộc miền nghiệm của bất phương trình nên bất phương trình cần tìm là −x+y≤1. Đáp án A Câu 30: Cho hệ bất phương trình {x−y≥−2x+y≤4x−5y≤−2. Giá trị lớn nhất của biểu thức F=−x+2y trên miền nghiệm của hệ bất phương trình
Phương pháp Để tìm giá trị lớn nhất của biểu thức F ta làm như sau: Bước 1: Xác định miền nghiệm của hệ bất phương trình trên, xác định các đỉnh của đa giác. Bước 2: Tính giá trị biểu thức F tại các đỉnh của đa giác đó. Bước 3: So sánh các giá trị thu được của F, giá trị lớn nhất của F là giá trị cần tìm. Lời giải Vẽ ba đường thẳng x−y=−2,x+y=4,x−5y=−2 và biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng tọa độ Oxy ta được: Miền nghiệm của hệ bất phương trình là miền tam giác ABC (kể cả các cạnh) với tọa độ các đỉnh A(1;3),B(−2;0),C(3;1). Tại A(1;3) ta có: F=−1+2.3=5 Tại B(−2;0) ta có: F=2+2.0=2 Tại C(3;1) ta có: F=−3+2.1=−1 Vậy giá trị lớn nhất của F là 5 tại x=1;y=3 Đáp án D Câu 31: Cho tam giác ABC. Chọn khẳng định đúng.
Phương pháp Áp dụng công thức: cotα=tan(900−α) Lời giải Ta có: ˆA+ˆB+ˆC=1800⇒ˆA=1800−(ˆB+ˆC)⇒ˆB+ˆC2=900−ˆA2 Do đó, cotA2=tan(900−A2)=tan(B+C2) Đáp án D Câu 32: Tính B=cos150+cos350−sin750−sin550
Phương pháp Sử dụng kiến thức sinα=cos(900−α) Lời giải B=cos150+cos350−sin750−sin550=(cos150−sin750)+(cos350−sin550) Mà cos150=sin(900−150)=sin750,cos350=sin(900−350)=sin550. Do đó, B=0 Đáp án C Câu 33: Cho tam giác ABC có AB=c,BC=a,AC=b. Biết rằng a2=b2+c2+√2bc. Tính số đo góc A.
Phương pháp Định lý côsin: Cho tam giác ABC có AB=c,BC=a,AC=b thì a2=b2+c2−2bccosA Lời giải Áp dụng định lí côsin vào tam giác ABC ta có: a2=b2+c2−2bccosA Mà a2=b2+c2+√2bc nên b2+c2+√2bc=b2+c2−2bccosA Suy ra: cosA=−√22 nên ˆA=1350 Đáp án B Câu 34: Cho hình vẽ dưới đây. Chọn đáp án đúng
Phương pháp Định lí sin: Cho tam giác ABC có AB=c,BC=a,AC=b. Khi đó, asinA=bsinB=csinC Lời giải Áp dụng định lí sin vào tam giác ABD ta có: ADsinB=BDsin^BAD=BDsin450=BD√2⇒sinB=ADBD√2 Áp dụng định lí sin vào tam giác ACD ta có: ADsinC=DCsin^CAD=BDsin600=2√3BD3 ⇒sinC=AD.√32BD Do đó: sinBsinC=√63 Đáp án A Câu 35: Cho tam giác ABC có AB=3cm,BC=5cm,CA=6cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Phương pháp Cho tam giác ABC có AB=c,BC=a,AC=b, bán kính đường tròn ngoại tiếp là R, p là nửa chu vi tam giác thì diện tích của tam giác là S=√p(p−a)(p−b)(p−c)=abc4R Lời giải Ta có: p=3+5+62=7cm Lại có: √7(7−3)(7−5)(7−6)=3.5.64R⇒R=45√1456cm Đáp án C Phần tự luận (3 điểm) Bài 1. (1,0 điểm) Thống kê tại một trung tâm mua sắm gồm 24 cửa hàng bán quần áo, 14 cửa hàng có bán giày và 30 cửa hàng bán ít nhất một trong hai mặt hàng này. Hỏi có bao nhiêu cửa hàng bán cả giày và quần áo? Phương pháp Tập hợp gồm những phần tử vừa thuộc A vừa thuộc B được gọi là giao của A và B, kí hiệu là A∩B. Lời giải Gọi x là số cửa hàng bán cả quần áo và giày, x là số tự nhiên. Số cửa hàng chỉ bán giày là: 14−x (cửa hàng), số cửa hàng chỉ bán quần áo là: 24−x (cửa hàng) Vì có 30 cửa hàng bán ít nhất một trong hai mặt hàng này nên ta có phương trình: 14−x+x+24−x=30 38−x=30 x=8 (thỏa mãn) Vậy có 8 cửa hàng bán cả quần áo và giày Bài 2. (1,0 điểm)
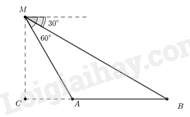
Phương pháp Định lý cosin: Cho tam giác ABC có AB=c,BC=a,AC=b thì a2=b2+c2−2bccosA Lời giải Ta có: ^AMB=600−300=300,^CMA=900−600=300,^CMB=300+300=600 Xét tam giác CMB vuông tại C có: ˆB=900−^CMB=900−600=300 Xét tam giác CMA vuông tại C có: MA=MCcos^CMA=9cos300=6√3(m) Xét tam giác ABM có: ^AMB=ˆB=300 nên tam giác ABM cân tại A. Do đó, AM=AB=6√3m≈10m Vậy khoảng cách giữa hai vận động viên là khoảng 10m. Bài 3. (1,0 điểm) Cho tam giác ABC, chứng minh nếu cos2A+cos2Bsin2A+sin2B=12(cot2A+cot2B) thì tam giác ABC là tam giác cân. Phương pháp Định lí sin: Cho tam giác ABC có AB=c,BC=a,AC=b, bán kính đường tròn ngoại tiếp tam giác ABC là R. Khi đó, asinA=bsinB=csinC=2R Lời giải Ta có: cos2A+cos2Bsin2A+sin2B=12(cot2A+cot2B) cos2A+cos2B+sin2A+sin2Bsin2A+sin2B=12(cot2A+1+cot2B+1) 2sin2A+sin2B=12(1sin2A+1sin2B) (sin2A+sin2B)2=4sin2Asin2B sin2A=sin2B⇔(a2R)2=(b2R)2⇔a=b Do đó, tam giác ABC cân tại C.
|