Phương pháp giải:

Sử dụng tính chất của nguyên hàm

Lời giải chi tiết:

\(\int {\left[ {f\left( x \right) - g\left( x \right)dx} \right]} \)\( = \int {f\left( x \right)dx}  - \int {g\left( x \right)dx} \)

Phương pháp giải:

Sử dụng bảng nguyên hàm.

Lời giải chi tiết:

\(\int {f\left( x \right)dx}  = \int {\cos xdx}  = \sin x + C\)

Phương pháp giải:

Tính chất của tích phân.

Lời giải chi tiết:

\(\int\limits_a^b {kf\left( x \right)dx}  = k\int\limits_a^b {f\left( x \right)dx} \)

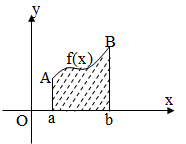
Phương pháp giải:

Tính chất của tích phân.

Diện tích hình giới hạn bởi đồ thị \(y = f\left( x \right)\) với trục hoành và các đường thẳng \(x = a;x = b\left( {a < b} \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)

Lời giải chi tiết:

\(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)\( = \int\limits_a^b {f\left( x \right)dx} \) do \(f\left( x \right) > 0\forall x \in \left[ {a;b} \right]\).

Phương pháp giải:

Công thức tính diện tích.

Lời giải chi tiết:

Diện tích hình giới hạn bởi đồ thị \(y = f\left( x \right)\) với trục hoành và các đường thẳng \(x = a;x = b\left( {a < b} \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).

Phương pháp giải:

Công thức tính thể tích.

Lời giải chi tiết:

\(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \).

Phương pháp giải:

Công thức tính diện tích hình giới hạn bởi 2 đồ thị hàm số.

Lời giải chi tiết:

\(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)

Phương pháp giải:

Số phức \(z = a + bi\left( {a,b \in \mathbb{R}} \right)\) có phần thực là a và phần ảo là b, i là đơn vị ảo.

Lời giải chi tiết:

Số phức \(z = 2 + 3i\) có phần thực là 2, phần ảo là 3.

Phương pháp giải:

Tìm mô đun của số phức

Lời giải chi tiết:

Mô đun của số phức là \(\left| z \right| = \sqrt {{a^2} + {b^2}} \).

Phương pháp giải:

Số phức liên hợp của \(z = a + bi\left( {a,b \in \mathbb{R}} \right)\) là \(\overline z  = a - bi\)

Lời giải chi tiết:

\(\overline z  = 2 - 3i\)

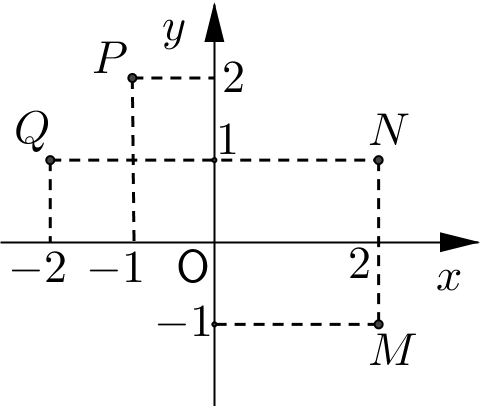
Phương pháp giải:

Số phức \(z = a + bi\left( {a,b \in \mathbb{R}} \right)\) có điểm biểu diễn là \(M\left( {a;b} \right)\)

Lời giải chi tiết:

\(z =  - 1 + 2i \Rightarrow \left\{ \begin{array}{l}x =  - 1\\y = 2\end{array} \right. \Rightarrow P\left( { - 1;2} \right)\)

Phương pháp giải:

Lấy phần thực cộng với phần thực, phần ảo cộng với phần ảo.

Lời giải chi tiết:

\(\begin{array}{l}{z_1} + {z_2} = \left( {2 + 3i} \right) + \left( {1 - 2i} \right)\\ = \left( {2 + 1} \right) + \left( {3i - 2i} \right) = 3 + i\end{array}\)

Phương pháp giải:

Nhân 2 số phức.

Lời giải chi tiết:

\(z = \left( {2 + i} \right)i = 2i + {i^2} = 2i - 1\)

Phương pháp giải:

Giải phương trình bậc hai \({z^2} =  - 4\)

Lời giải chi tiết:

\(\begin{array}{l}{z^2} =  - 4 \Leftrightarrow {z^2} = {\left( {2i} \right)^2}\\ \Leftrightarrow \left[ \begin{array}{l}z = 2i\\z =  - 2i\end{array} \right.\end{array}\)

Phương pháp giải:

Tích vô hướng của hai vecto \(\overrightarrow u \left( {a;b;c} \right),\overrightarrow n \left( {x;y;z} \right)\) là: \(\overrightarrow u .\overrightarrow v  = ax + by + cz\).

Lời giải chi tiết:

\(\overrightarrow a .\overrightarrow b  = 1.3 + 2.\left( { - 2} \right) + \left( { - 3} \right).\left( { - 1} \right) = 2\)

Phương pháp giải:

Điểm \(M\left( {{x_0},{y_0},{z_0}} \right) \in \left( P \right):ax + by + cz = 0\)\( \Leftrightarrow a{x_0} + b{y_0} + c{z_0} = 0\).

Lời giải chi tiết:

Thay lần lượt tọa độ các điểm vào \(\left( \alpha  \right)\) ta thấy:

\(1 - 2.\left( { - 2} \right) + 3.\left( { - 1} \right) - 2 = 0\)

Điểm N thuộc \(\left( \alpha  \right)\).

Phương pháp giải:

Hai mặt phẳng (P): \({a_1}x + {b_1}y + {c_1}z + {d_1} = 0\) và (Q): \({a_2}x + {b_2}y + {c_2}z + {d_2} = 0\)\(\left( {{a_1},{b_2},{c_2},{d_2} \ne 0} \right)\) song song khi và chỉ khi: \(\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}} \ne \frac{{{d_1}}}{{{d_2}}}\)

Lời giải chi tiết:

\({\overrightarrow n _{\left( \alpha  \right)}} = \left( {2;3; - 1} \right)\). Ta có:

Đáp án A sai vì mặt phẳng này trùng với  \(\left( \alpha  \right)\).

Đáp án B, D sai vì vecto pháp tuyến của mặt phẳng này không song song với \({\overrightarrow n _{\left( \alpha  \right)}}\).

Đáp án C đúng vì \(\overrightarrow n  = \left( { - 4; - 6;2} \right)\). Khi đó

\(\frac{{ - 4}}{2} = \frac{{ - 6}}{2} = \frac{2}{{ - 1}} \ne \frac{2}{1}\)

Phương pháp giải:

Điểm \(M\left( {m,n,p} \right) \in d:\)\(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\)\( \Leftrightarrow \frac{{m - {x_0}}}{a} = \frac{{n - {y_0}}}{b} = \frac{{p - {z_0}}}{c}\).

Lời giải chi tiết:

Thay lần lượt các đáp án vào d:

Ta thấy khi thay P vào d thì có : \(\frac{{7 - 1}}{3} = \frac{4}{2} \ne \frac{{ - 7 + 1}}{3}\)

Phương pháp giải:

Vecto chỉ phương của đường thẳng \(d:\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\left( {t \in \mathbb{R}} \right)\) là \(\overrightarrow u  = \left( {a;b;c} \right)\)

Lời giải chi tiết:

\(\overrightarrow u  = \left( {1; - 1;2} \right)\)

Phương pháp giải:

Đường thẳng qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và nhận \(\overrightarrow u  = \left( {a;b;c} \right)\) làm vecto chỉ phương là:

\(d:\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\left( {t \in \mathbb{R}} \right)\).

Lời giải chi tiết:

Đường thẳng qua M(3; -2; 1)  và nhận \(\overrightarrow u  = \left( {4; - 3;5} \right)\) làm vecto chỉ phương là:

\(\left\{ {\begin{array}{*{20}{c}}{x = 3 + 4t}\\{y =  - 2 - 3t}\\{z = 1 + 5t}\end{array}} \right.\)

Phương pháp giải:

Áp dụng công thức:

\(\int {{e^{ax + b}}dx}  = \frac{1}{a}{e^{ax + b}} + C\)

Lời giải chi tiết:

\(\int {f\left( x \right)dx}  = \int {{e^{2x}}dx}  = \frac{1}{2}{e^{2x}} + C\)

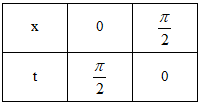
Phương pháp giải:

Đặt \(t = {x^2} \Rightarrow dx = 2tdt\).

Đổi cận ẩn x sang ẩn t.

Đưa tích phân về ẩn t.

Lời giải chi tiết:

Đặt \(t = {x^2} \Rightarrow dx = 2tdt\)

Đổi cận:

\( =  > I = \frac{1}{2}\int\limits_0^4 {{e^t}dt} \)

Phương pháp giải:

Sử dụng bảng nguyên hàm: \(I = \int {{2^x}dx}  = \frac{{{2^x}}}{{\ln 2}} + C\)

Lời giải chi tiết:

\(I = \int\limits_0^1 {{2^x}dx}  = \left. {\frac{{{2^x}}}{{\ln 2}}} \right|_0^1 = \frac{1}{{\ln 2}}\)x.

Phương pháp giải:

Sử dụng phương pháp tích phân từng phần.

Lời giải chi tiết:

\(\begin{array}{l}I = \int\limits_1^3 {x\ln xdx} \\ = \int\limits_1^3 {\frac{1}{2}\ln x} d{x^2}\\ = \left. {\frac{{{x^2}\ln x}}{2}} \right|_1^3 - \frac{1}{2}\int\limits_1^3 {{x^2}d\left( {\ln x} \right)} \\ = \left. {\frac{{{x^2}\ln x}}{2}} \right|_1^3 - \frac{1}{2}\int\limits_1^3 {xdx} \end{array}\)

Phương pháp giải:

Diện tích hình phẳng bằng: \(\int_a^c {\left| {f\left( x \right)} \right|dx = \int_a^b {\left| {f\left( x \right)} \right|dx} } \)\( + \int_b^c {\left| {f\left( x \right)} \right|dx} \)

Xét dấu của f(x) trong [a;b] và [b;c].

\(\left| {f\left( x \right)} \right| = f\left( x \right) \Leftrightarrow \) đồ thị nằm bên trên trục Ox.

\(\left| {f\left( x \right)} \right| =  - f\left( x \right) \Leftrightarrow \) đồ thị nằm bên dưới trục Ox.

Lời giải chi tiết:

\(S = \int_a^c {\left| {f\left( x \right)} \right|dx = \int_a^b {\left| {f\left( x \right)} \right|dx} } \)\( + \int_b^c {\left| {f\left( x \right)} \right|dx} \)

\(\begin{array}{l} = \int_a^b { - f\left( x \right)dx}  + \int_b^c {f\left( x \right)dx} \\ = 2 + 3 = 5\end{array}\)

Phương pháp giải:

Tính diện tích \(S\) hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng\(x = a,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)

Xét dấu của f(x) trong [a;b].

Lời giải chi tiết:

\(S = \int\limits_0^1 {\left| {{x^2} - 4} \right|dx}  = \int\limits_0^1 {\left( {4 - {x^2}} \right)dx}  = \frac{{11}}{3}\)

Phương pháp giải:

Số thuần ảo là số có dạng  \(z = bi,\left( {b \in \mathbb{R}} \right)\)

Lời giải chi tiết:

\(z = i\) là số thuần ảo.

Phương pháp giải:

Tập hợp điểm biểu diễn z thỏa mãn \(\left| {z - {z_0}} \right| = R\) là đường tròn tâm \(M\left( {{z_0}} \right)\) bán kính R.

Lời giải chi tiết:

\(\left| {z - 1} \right| = 2 \Leftrightarrow \left| {z - \left( {1 + 0.i} \right)} \right| = 2\)

=> Tập hợp điểm biểu diễn z là đường tròn tâm I(1;0) bán kính 2.

Phương pháp giải:

Đặt \(z = a + bi,\left( {a,b \in \mathbb{R}} \right)\)

Tìm \(\overline z \) và sử dụng cách đồng nhất hệ số để tìm a và b.

Lời giải chi tiết:

Đặt \(z = a + bi,\left( {a,b \in \mathbb{R}} \right)\)

\(\begin{array}{l}2z + \overline z  = 3 + 4i\\ \Leftrightarrow 2\left( {a + bi} \right) + a - bi = 3 + 4i\\ \Leftrightarrow 3a + bi = 3 + 4i\\ \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 4\end{array} \right. \Rightarrow z = 1 + 4i\end{array}\)

Phương pháp giải:

Sử dụng tính chất \(z.{z_1} = {z_2} \Leftrightarrow z = \frac{{{z_2}}}{{{z_1}}}\) và \(\frac{1}{z} = \frac{{\overline z }}{{{{\left| z \right|}^2}}}\).

Phần thực của số phức \(z = a + bi\) là a.

Lời giải chi tiết:

\(\begin{array}{l}i.z = 1 + 2i\\ \Leftrightarrow z = \frac{{1 + 2i}}{1}\\ \Leftrightarrow z = \frac{{\left( {1 + 2i} \right)\left( { - i} \right)}}{1}\\ \Leftrightarrow z = 2 - i\end{array}\)

=> Phần thực là 2.

Phương pháp giải:

\({z_1},{z_2}\) là hai nghiệm phức của phương trình \(a{z^2} + bz + c = 0\)  thì \(\left| {{z_1}} \right| = \left| {{z_2}} \right|\) và

\({z_1}.{z_2} = \frac{c}{a}\)

Lời giải chi tiết:

\({z_1},{z_2}\) là hai nghiệm phức của phương trình \({z^2} + 2z + 5 = 0\) nên \(\left| {{z_1}} \right| = \left| {{z_2}} \right|\).

Mà theo Vi-et ta có: \({z_1}.{z_2} = 5 =  > \left| {{z_1}.{z_2}} \right| = \left| 5 \right|\).

=> \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \sqrt 5  \Rightarrow \left| {{z_1}} \right| + \left| {{z_2}} \right| = 2\sqrt 5 \)

Phương pháp giải:

Đưa phương trình mặt cầu về dạng \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).

Lời giải chi tiết:

\(\begin{array}{l}{x^2} + {y^2} + {z^2} + 2z - 4y - 2 = 0\\ \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 7\end{array}\)

=> (S) là mặt cầu tâm \(I\left( { - 1;2;0} \right)\) bán kính \(R = \sqrt 7 \).

Phương pháp giải:

Mặt phẳng (Oxy) có một véc tơ pháp tuyến \(\overrightarrow k  = \left( {0,0,1} \right)\).

Lời giải chi tiết:

Mặt phẳng (Oxy) có một véc tơ pháp tuyến \(\overrightarrow n  = \left( {0,0,1} \right)\)

Phương pháp giải:

Khoảng cách từ điểm \(M\left( {{x_0},{y_0},{z_0}} \right)\) đến mặt phẳng \(\left( P \right):ax + by + cz + d = 0\) bằng:

\(d\left( {M,\left( P \right)} \right) = \frac{{\left| {a{x_0} + b{y_0} + c{z_0} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)

Lời giải chi tiết:

Khoảng cách từ điểm \(M\left( {1;2;3} \right)\) đến mặt phẳng \(\left( P \right):x + 2y + 2z - 1 = 0\) bằng

\(d\left( {M,\left( P \right)} \right) = \frac{{\left| {1 + 2.2 + 2.3 - 1} \right|}}{{\sqrt {1 + 4 + 4} }}\)\( = \frac{{10}}{3}\)

Phương pháp giải:

Tìm \(\overrightarrow {MN} \).

Đường thẳng đi qua 2 điểm M,N nhận \(k.\overrightarrow {MN} \left( {k \ne 0} \right)\) làm vecto chỉ phương.

Lời giải chi tiết:

\(\overrightarrow {MN}  = \left( {2;2;8} \right)\)

Đường thẳng đi qua 2 điểm M,N nhận \(\overrightarrow u  = \left( {1;1;4} \right)\) làm vecto chỉ phương nên loại C, D.

Thay tọa độ điểm M vào đáp án A ta tìm được \(t =  - 1\).

Phương pháp giải:

Biến đổi \(\sqrt {x + 1}  = {\left( {x + 1} \right)^{\frac{1}{2}}}\).

Sử dụng công thức \(\int {{{\left( {ax + b} \right)}^m}dx}  = \frac{1}{a}.\frac{{{{\left( {ax + b} \right)}^{m + 1}}}}{{m + 1}} + C\)

Lời giải chi tiết:

\(\begin{array}{l}\int {\sqrt {x + 1} dx}  = \int {{{\left( {x + 1} \right)}^{\frac{1}{2}}}dx} \\ = \frac{{{{\left( {x + 1} \right)}^{\frac{3}{2}}}}}{{\frac{3}{2}}} + C\\ = \frac{2}{3}\left( {x + 1} \right)\sqrt {x + 1}  + C\end{array}\)

Phương pháp giải:

Số phức liên hợp của \(z = a + bi\left( {a,b \in \mathbb{R}} \right)\) là \(\overline z  = a - bi\)

Thay vào biểu thức \(i.z + 2.\overline z  = 6 + 3i\) tìm a và b.

Lời giải chi tiết:

\(\begin{array}{l}i.z + 2.\overline z  = 6 + 3i\\ \Leftrightarrow i\left( {a + bi} \right) + 2\left( {a - bi} \right) = 6 + 3i\\ \Leftrightarrow \left( {a - 2b} \right)i + 2a - b = 6 + 3i\\ \Leftrightarrow \left\{ \begin{array}{l}a - 2b = 3\\2a - b = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = 0\end{array} \right.\end{array}\)

\( \Rightarrow a - b = 3\)

Phương pháp giải:

Tìm hoành độ giao điểm của 2 đồ thị \(y = 1 - {x^2},\,y = 0\).

Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = 0\) , \(x = a,x = b\left( {a < b} \right)\) quanh trục \(Ox\) là \(I = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)

Lời giải chi tiết:

Hoành độ giao điểm của 2 đồ thị \(y = 1 - {x^2},y = 0\) là nghiệm của phương trình:

\(1 - {x^2} = 0 \Leftrightarrow x =  \pm 1\)

Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường \(y = 1 - {x^2},y = 0\) quanh trục \(Ox\) là

\(\begin{array}{l}I = \pi \int\limits_{ - 1}^1 {{{\left( {1 - {x^2}} \right)}^2}dx} \\ = \frac{{16\pi }}{{15}}\end{array}\)

Phương pháp giải:

Tách tích phân thành \(\int\limits_1^4 {1dx}  + \int\limits_1^4 {\frac{{f\left( {\sqrt x } \right)}}{{\sqrt x }}dx} \)

Đổi biến số \(t = \sqrt x \) tính \(\int\limits_1^4 {\frac{{f\left( {\sqrt x } \right)}}{{\sqrt x }}dx} \).

Lời giải chi tiết:

\(\begin{array}{l}I = \int\limits_1^4 {\frac{{\sqrt x  + f\left( {\sqrt x } \right)}}{{\sqrt x }}dx} \\ = \int\limits_1^4 {1dx}  + \int\limits_1^4 {\frac{{f\left( {\sqrt x } \right)}}{{\sqrt x }}dx} \\ = 3 + 2\int\limits_1^4 {f\left( {\sqrt x } \right)d\left( {\sqrt x } \right)} \end{array}\)

Đặt \(t = \sqrt x \)

Đổi cận:

\( =  > I = 3 + 2\int\limits_1^2 {f\left( t \right)dt}  = 3 + 2.2 = 7\)

Phương pháp giải:

Nhân 2 vế với i.

Đặt \(z = a + bi\left( {a,b \in \mathbb{R}} \right)\)

Biếnđổi biểu thức rồi đồng nhất hệ số tìm \({a^2},{b^2}\).

Mô đun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \).

Lời giải chi tiết:

\(\frac{{2z}}{i} + \left| z \right|.i = 3\). Nhân 2 vế với i.

Ta được:

\(2z - \left| z \right| = 3i\)

Đặt \(z = a + bi\left( {a,b \in \mathbb{R}} \right)\)

\(\begin{array}{l}2z - \left| z \right| = 3i\\ \Leftrightarrow 2\left( {a + bi} \right) - \sqrt {{a^2} + {b^2}}  = 3i\\ \Leftrightarrow \left\{ \begin{array}{l}2a - \sqrt {{a^2} + {b^2}}  = 0\\2b = 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a \ge 0\\{a^2} + {b^2} = 4{a^2}\\b = \frac{3}{2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{a^2} = \frac{3}{4}\\b = \frac{3}{2}\end{array} \right.\\ \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}}  = \sqrt 3 \\ \Rightarrow 1 < \left| z \right| < 2\end{array}\)

Phương pháp giải:

Giải phương trình trùng phương \(a{x^4} + b{x^2} + c = 0\) tìm nghiệm phức có phần ảo dương.

Lời giải chi tiết:

\(\begin{array}{l}{z^4} + {z^2} - 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{z^2} = 2\\{z^2} =  - 3 = {\left( {\sqrt 3 i} \right)^2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z = \sqrt 2 \\z =  - \sqrt 2 \\z = \sqrt 3 i\\z =  - \sqrt 3 i\end{array} \right.\\ \Rightarrow {z_0} = \sqrt 3 i \Rightarrow i{z_0} =  - \sqrt 3 \end{array}\)

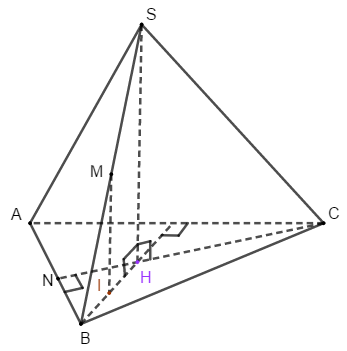
Phương pháp giải:

Mặt cầu đường kính AB có tâm là M bán kính \(R = \frac{{AB}}{2}\)

Lời giải chi tiết:

M là trung điểm của AB

=> \(M\left( { - 1;2;1} \right)\).

Mặt cầu đường kính AB có tâm là M bán kính \(R = \frac{{AB}}{2} = \sqrt {21} \) là:

\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 21\)

Phương pháp giải:

SA, SB, SC đôi một vuông góc nên \(SH \bot \left( {ABC} \right)\). Với H là trực tâm của tam giác ABC.

Tìm SH.

Kẻ \(CN \bot AB\) và chứng minh \(AB \bot SN\).

Tam giác \(SAB\) đường cao SN ứng với cạnh huyền có: \(\frac{1}{{S{N^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{S{B^2}}}\).

Lời giải chi tiết:

SA, SB, SC đôi một vuông góc nên \(SH \bot \left( {ABC} \right)\). Với H là trực tâm của tam giác ABC.

Goi I là trung điểm của BH.

=> MI//SH

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}SH = 2MI\\MI \bot \left( {ABC} \right)\end{array} \right.\\ \Rightarrow MI = d\left( {M,\left( {ABC} \right)} \right) = \frac{2}{3}\\ \Rightarrow SH = 2MI = \frac{4}{3}\end{array}\)

Kẻ \(CN \bot AB\)

\(\begin{array}{l}SC \bot AB\\ \Rightarrow AB \bot \left( {SCN} \right)\\ \Rightarrow AB \bot SN\end{array}\)

\(\begin{array}{l} \Rightarrow \frac{1}{{S{N^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{S{B^2}}} = \frac{5}{{16}}\\ \Rightarrow \frac{1}{{S{C^2}}} = \frac{1}{{S{H^2}}} - \frac{1}{{S{N^2}}} = \frac{1}{4}\\ \Rightarrow SC = 2\end{array}\)

Phương pháp giải:

Tìm \({\overrightarrow u _d}\) và \({\overrightarrow u _{d'}}\). Nhận xét mối quan hệ giữa \({\overrightarrow u _d}\) và \({\overrightarrow u _{d'}}\) suy ra mối quan hệ giữa \(d\) và \(d'\) .

Lời giải chi tiết:

\(\begin{array}{l}{\overrightarrow u _d} = \left( {2; - 1; - 3} \right),{\overrightarrow u _{d'}} = \left( { - 2;1;3} \right)\\ \Rightarrow {\overrightarrow u _d}//{\overrightarrow u _{d'}} \Rightarrow d//d'\end{array}\)

Phương pháp giải:

Tìm \({\overrightarrow u _\Delta }\)

\(\overrightarrow u \) là một véc tơ chỉ phương của đường thẳng d đi qua điểm A, vuông góc với đường thẳng \(\Delta \)nên \(\overrightarrow u  \bot {\overrightarrow u _\Delta } \Rightarrow \overrightarrow u .{\overrightarrow u _\Delta } = 0\).

Lập hệ phương trình giao điểm của d cắt Oy.

Tìm a,b.

Lời giải chi tiết:

\({\overrightarrow u _\Delta } = \left( {1; - 2;2} \right)\)

\(\overrightarrow u  = \left( {a;b;3} \right)\) là một véc tơ chỉ phương của đường thẳng d đi qua điểm A, vuông góc với đường thẳng \(\Delta \)nên \(\overrightarrow u  \bot {\overrightarrow u _\Delta } \Rightarrow \overrightarrow u .{\overrightarrow u _\Delta } = 0\).

Hay \(a - 2b + 6 = 0 \Leftrightarrow a = 2b - 6\)

Có \(d:\left\{ \begin{array}{l}x = 2 + at\\y = 1 + bt\\z = 3 + 3t\end{array} \right.\)

Vì d cắt Oy nên hệ phương trình \(\left\{ \begin{array}{l}2 + at = 0\\1 + bt = t'\\3 + 3t = 0\end{array} \right.\) có nghiệm

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}at =  - 2\\bt = t' - 1\\t =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 4\\t =  - 1\\t' =  - 3\end{array} \right.\\ \Rightarrow a + b = 6\end{array}\)

Phương pháp giải:

+ Tìm hoành độ giao điểm của đường thẳng \(y = mx\) và đồ thị hàm số \(y = {x^2}\) .

+ Diện tích hình phẳng giới hạn bởi đường thẳng \(y = f\left( x \right)\) (\(m\) là tham số dương) và đồ thị hàm số \(y = g\left( x \right)\) và các đường thẳng \(x = a,x = b\left( {a < b} \right)\)bằng \(I = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)

Giải phương trình \(I = 1\) tìm m.

Lời giải chi tiết:

Hoành độ giao điểm của đường thẳng \(y = mx\) và đồ thị hàm số \(y = {x^2}\) là nghiệm của phương trình \({x^2} = mx \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = m\end{array} \right.\)

Diện tích hình phẳng giới hạn bởi đường thẳng \(y = mx\) (\(m\) là tham số dương) và đồ thị hàm số \(y = {x^2}\) bằng

\(\begin{array}{l}I = \int\limits_0^m {\left| {{x^2} - mx} \right|dx} \\ = \int\limits_0^m {\left( {mx - {x^2}} \right)dx} \\ = \frac{{{m^3}}}{6}\\ \Rightarrow \frac{{{m^3}}}{6} = 1 \Leftrightarrow m = \sqrt[3]{6}\end{array}\)

Phương pháp giải:

+ Sử dụng phương pháp tích phân từng phần u=x,v=f(x).

+ Đổi biến số \(t = \frac{\pi }{2} - x\)

+ Sử dụng tính chất \(\int\limits_a^b {f\left( x \right)dx}  = \int\limits_a^b {f\left( t \right)dt} \).

Lời giải chi tiết:

\(\begin{array}{l}I = \int\limits_0^{\frac{\pi }{2}} {xf'\left( x \right)dx}  = \int\limits_0^{\frac{\pi }{2}} {xd\left[ {f\left( x \right)} \right]} \\ = x.f\left( x \right) - \int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx}  =  - \int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx} \end{array}\)

Ta có \(f\left( x \right) + f\left( {\frac{\pi }{2} - x} \right) = \sin x.\cos x\) nên

\(f\left( x \right) = \sin x.\cos x - f\left( {\frac{\pi }{2} - x} \right)\) thay vào I ta được:

\(I = \int\limits_0^{\frac{\pi }{2}} {\left[ {f\left( {\frac{\pi }{2} - x} \right) - \sin x.\cos x} \right]dx} \)

Đặt \(t = \frac{\pi }{2} - x \Rightarrow x = \frac{\pi }{2} - t \Rightarrow dx =  - dt\)

Đổi cận:

\(\begin{array}{l}I = \int\limits_{\frac{\pi }{2}}^0 {\left[ {f\left( t \right) - \sin \left( {\frac{\pi }{2} - t} \right).\cos \left( {\frac{\pi }{2} - t} \right)} \right]\left( { - tdt} \right)} \\ = \int\limits_0^{\frac{\pi }{2}} {\left[ {f\left( t \right) - \sin t.\cos t} \right]dt} \\ = \int\limits_0^{\frac{\pi }{2}} {\left[ {f\left( x \right) - \sin x.\cos x} \right]dx} \\ = \int\limits_0^{\frac{\pi }{2}} { - \sin x.\cos x}  - I =  - \frac{1}{2} - I\\ \Rightarrow I =  - \frac{1}{4}\end{array}\)

Phương pháp giải:

Sử dụng các tính chất: \(\frac{z}{{{{\left| z \right|}^2}}} = \frac{1}{{\overline z }};\left| z \right| = \left| {\overline z } \right|\), \(\left| {{z_1}.{z_2}} \right| = \left| {{z_1}} \right|.\left| {{z_2}} \right|\)

Lời giải chi tiết:

\(\begin{array}{l}\frac{{1 + 2i}}{{\bar z}} = \frac{{\left( {1 - i} \right).z}}{{{{\left| z \right|}^2}}} + 1 + 3i\\ \Leftrightarrow \frac{{1 + 2i}}{{\bar z}} = \frac{{\left( {1 - i} \right)}}{{\overline z }} + 1 + 3i\\ \Leftrightarrow \frac{{1 + 2i - 1 + i}}{{\overline z }} = 1 + 3i\\ \Leftrightarrow \frac{{3i}}{{\overline z }} = 1 + 3i\\ \Rightarrow \frac{{\left| {3i} \right|}}{{\left| {\overline z } \right|}} = \left| {1 + 3i} \right|\\ \Leftrightarrow \left| z \right| = \left| {\overline z } \right| = \frac{{\sqrt {10} }}{3}\end{array}\)

Phương pháp giải:

Đặt \({\rm{w}} = x + yi\).

Đưa về dạng \(z.{z_1} = {z_2}\) rồi lấy mô đun 2 vế.

Biện luận \({\left| z \right|^2}\)

Sử dụng bất đẳng thức \(\left| {{z_1} \pm {z_2}} \right| \le \left| {{z_1}} \right| + \left|{{z_2}} \right|\).

Lời giải chi tiết:

Đặt \(w= x + yi\).

Từ giả thiết \(w= \frac{{1 + iz}}{{2 + z}} \Rightarrow w\left( {2 + z} \right) = 1 + iz\)

\( \Rightarrow z\left( w- i \right) = 1 - 2w\)

\( \Rightarrow z\left[ {x + yi - i} \right] = 1 - 2\left( {x + yi} \right)\)  (1)

Lấy modun hai vế biểu thức (1) ta được 

\(\left| z \right|\sqrt {{x^2} + {{\left( {y - 1} \right)}^2}}  = \sqrt {{{\left( {1 - 2x} \right)}^2} + {{\left( { - 2y} \right)}^2}} \)

\( \Rightarrow {\left| z \right|^2}\left( {{x^2} + {y^2} - 2y + 1} \right)\)\( = \left( {4{x^2} + 4{y^2} - 4x + 1} \right)\)  (2)

Từ (2) suy ra:

Nếu \({\left| z \right|^2} \ne 4\) thì tập hợp các điểm biểu diễn số phức \(w\) là đường tròn.

Nếu \({\left| z \right|^2} = 4\) thì tập hợp các điểm biểu diễn số phức \({\rm{w}}\) là đường thẳng thỏa mãn đề bài.

Suy ra \(\left| z \right| = 2\)

+ \(P = \left| {z - 4i} \right| \le \left| z \right| + \left| {4i} \right| = 6\) . Dấu “=” xảy ra khi \(z =  - 2i\) vì z phải là số thuần ảo giống -4i. Vậy GTLN của P bằng \(6\).

Phương pháp giải:

+ Gọi H là hình chiếu vuông góc của M lên đường thẳng d. Khi đó mp (P) thỏa yêu cầu bài toán vuông góc với MH tại H.

+ Tìm tọa độ điểm H sau đó viết ptmp (P)

Lời giải chi tiết:

Gọi H là hình chiếu vuông góc của M lên đường thẳng d.

Goi (Q) là mặt phẳng qua M và vuông góc với d. Khi đó \(\left( Q \right) \cap d = \left\{ H \right\}\)

\(\begin{array}{l}\left( Q \right):0\left( {x - 1} \right) + \left( {y - 1} \right) - \left( {z - 2} \right) = 0\\ \Leftrightarrow y - z + 1 = 0\end{array}\)

\( \Rightarrow H\left( {1;0;1} \right) \Rightarrow MH = \left( {0; - 1; - 1} \right)\)

Mặt phẳng (P) chứa đường thẳng d và cách điểm M một khoảng lớn nhất khi và chỉ khi \(MH \bot \left( P \right)\) tại H. Hay

\(\begin{array}{l}\left( P \right):0\left( {x - 1} \right) + \left( {y - 0} \right) + \left( {z - 1} \right) = 0\\ \Leftrightarrow 0x + y + z - 1 = 0\end{array}\)

\( \Rightarrow T = a + b + c = 0 + 1 + 1 = 2\)