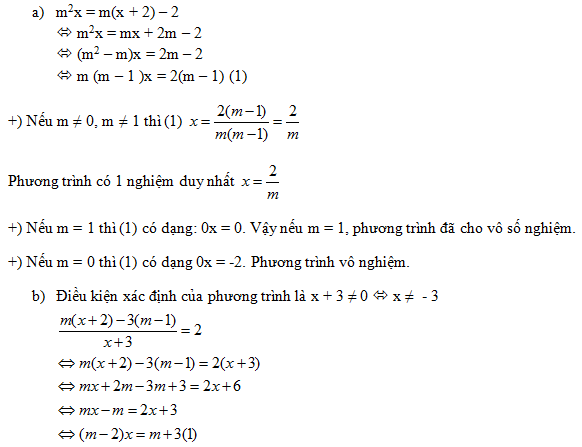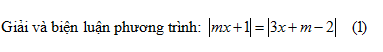60 bài tập trắc nghiệm phương trình mức độ vận dụngLàm bàiCâu hỏi 1 : Phương trình \({\left( {x + 1} \right)^2} = 3x + 9\) là phương trình hệ quả của phương trình nào sau đây?
Đáp án: C Phương pháp giải: \(\begin{array}{l} + )\,\,{\left( {x + 1} \right)^2} = 3x + 9 \Leftrightarrow {x^2} - x - 8 = 0 \Leftrightarrow x = \frac{{1 \pm \sqrt {33} }}{2}\\ + )\,\,\sqrt {x + 1} = 3x - 9 \Leftrightarrow \left\{ \begin{array}{l}3x + 9 \ge 0\\x + 1 = 9{x^2} - 54x + 81\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 3\\x = \frac{{55 \pm \sqrt {145} }}{{18}}\end{array} \right.\\ + )\,\,\sqrt {x + 1} = \sqrt {3x - 9} \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\3x - 9 \ge 0\\x + 1 = 3x - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\x \ge 3\\2x = 10\end{array} \right. \Leftrightarrow x = 5\\ + )\,\,x + 1 = \sqrt {3x + 9} \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\{x^2} + 2x + 1 = 3x + 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\{x^2} - x - 8 = 0\end{array} \right. \Leftrightarrow x = \frac{{1 + \sqrt {33} }}{2}\\ + )\,\,x + 1 = 3\left( {x + 3} \right) \Leftrightarrow x + 1 = 3x + 9 \Leftrightarrow 2x = - 8 \Leftrightarrow x = - 4\end{array}\) Vậy phương trình \({\left( {x + 1} \right)^2} = 3x + 9\) là phương trình hệ quả của phương trình \(x + 1 = \sqrt {3x + 9} \). Chọn đáp án C. Lời giải chi tiết: Nếu mọi nghiệm của phương trình \(f\left( x \right) = 0\) đều là nghiệm của phương trình \(g\left( x \right) = 0\) thì \(g\left( x \right) = 0\) được gọi là phương trình hệ quả của phương trình \(f\left( x \right) = 0\). Câu hỏi 2 : Giải phương trình \({x^2} + \frac{1}{{\sqrt {1 - x} }} = 3x + \frac{1}{{\sqrt {1 - x} }}\,\,\,\left( 1 \right)\)
Đáp án: A Phương pháp giải: +) Tìm TXĐ. +) Rút gọn và giải phương trình. Lời giải chi tiết: ĐK: \(1 - x > 0 \Leftrightarrow x < 1\) \({x^2} + \frac{1}{{\sqrt {1 - x} }} = 3x + \frac{1}{{\sqrt {1 - x} }} \Leftrightarrow {x^2} - 3x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\left( {tm} \right)\\x = 3\,\,\left( {ktm} \right)\end{array} \right.\) Vậy \(x = 1\) là nghiệm của phương trình. Câu hỏi 3 : Khẳng định nào sau đây là sai?
Đáp án: C Phương pháp giải: Dựa vào khái niệm phương trình hệ quả: Nếu mỗi nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) đều là nghiệm của phương trình \(h\left( x \right) = k\left( x \right)\) thì phương trình \(h\left( x \right) = k\left( x \right)\) được gọi là phương trình hệ quả của phương trình \(f\left( x \right) = g\left( x \right)\) (nghĩa là tập hợp nghiệm của phương trình \(h\left( x \right) = k\left( x \right)\) chứa tập nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\)). Lời giải chi tiết: Xét đáp án C ta có: \(\begin{array}{l} + )\,\,\left| {3x - 2} \right| = x - 3 \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\{\left( {3x - 2} \right)^2} = {\left( {x - 3} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\{\left( {3x - 2} \right)^2} - {\left( {x - 3} \right)^2} = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left( {4x - 5} \right)\left( {2x + 1} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = \dfrac{5}{4}\\x = - \dfrac{1}{2}\end{array} \right.\,\,\left( {ktm} \right)\end{array} \right. \Leftrightarrow x \in \emptyset \Rightarrow {S_1} = \emptyset \\ + )\,\,8{x^2} - 4x - 5 = 0 \Leftrightarrow x = \dfrac{{1 \pm \sqrt {11} }}{4} \Rightarrow {S_2} = \left\{ {\dfrac{{1 \pm \sqrt {11} }}{4}} \right\}\end{array}\) Do nên đáp án C sai. Chọn C. Câu hỏi 4 : Cho hai phương trình \(x\left( {x - 2} \right) = 3\left( {x - 2} \right)\) (1) và \(\dfrac{{x\left( {x - 2} \right)}}{{x - 2}} = 3\,\,\left( 2 \right)\). Khẳng định nào sau đây là đúng?
Đáp án: A Phương pháp giải: Xác định tập nghiệm của mỗi phương trình (1) và (2) sau đó dựa vào khái niệm phương trình hệ quả để kết luận. Lời giải chi tiết: Xét phương trình (1) ta có \(x\left( {x - 2} \right) = 3\left( {x - 2} \right) \Leftrightarrow \left( {x - 2} \right)\left( {x - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 3\end{array} \right. \Rightarrow {S_1} = \left\{ {2;3} \right\}\). Xét phương trình (2) ta có: ĐK: \(x - 2 \ne 0 \Leftrightarrow x \ne 2\). \(\dfrac{{x\left( {x - 2} \right)}}{{x - 2}} = 3 \Leftrightarrow \dfrac{{x\left( {x - 2} \right) - 3\left( {x - 2} \right)}}{{x - 2}} = 0 \Leftrightarrow \left( {x - 2} \right)\left( {x - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {ktm} \right)\\x = 3\,\,\left( {tm} \right)\end{array} \right. \Rightarrow {S_2} = \left\{ 3 \right\}\). Vì \({S_2} \subset {S_1}\) nên phương trình phương trình (1) là phương trình hệ quả của phương trình (2). Chọn A. Câu hỏi 5 : Phương trình \(\left( {{x^2} - x - 2} \right)\sqrt {x + 1} = 0\) có bao nhiêu nghiệm?
Đáp án: C Phương pháp giải: Giải phương trình dạng \(f\left( x \right)g\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\g\left( x \right) = 0\end{array} \right.\). Lưu ý ĐKXĐ của phương trình. Lời giải chi tiết: ĐKXĐ: \(x + 1 \ge 0 \Leftrightarrow x \ge - 1\). \(\left( {{x^2} - x - 2} \right)\sqrt {x + 1} = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} - x - 2 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left( {x + 1} \right)\left( {x - 2} \right) = 0\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\,\,\left( {tm} \right)\). Vậy phương trình đã cho có 2 nghiệm. Chọn C. Câu hỏi 6 : Khẳng định nào sau đây là sai?
Đáp án: D Phương pháp giải: Hai phương trình được gọi là tương đương khi chúng có cùng tập hợp nghiệm. Lời giải chi tiết: Xét đáp án D ta có \({x^2} = 1 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x + 1} \right) = 0 \Leftrightarrow x = \pm 1\). Do đó đáp án D sai. Chọn D. Câu hỏi 7 : Điều kiện xác định của phương trình \(\dfrac{{\sqrt {2x + 1} }}{{{x^2} + 3x}} = 0\) là:
Đáp án: C Phương pháp giải: +) \(\sqrt A \) xác định (có nghĩa) \( \Leftrightarrow A \ge 0\). +) Phân thức xác định khi và chỉ khi mẫu thức khác 0. Lời giải chi tiết: Phương trình xác định \( \Leftrightarrow \left\{ \begin{array}{l}2x + 1 \ge 0\\{x^2} + 3x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{{ - 1}}{2}\\x \ne 0\\x \ne - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{{ - 1}}{2}\\x \ne 0\end{array} \right.\). Chọn C. Câu hỏi 8 : Điều kiện xác định của phương trình \(x + 2 - \dfrac{1}{{\sqrt {x + 2} }} = \dfrac{{\sqrt {4 - 3x} }}{{x + 1}}\) là:
Đáp án: C Phương pháp giải: +) \(\sqrt A \) xác định (có nghĩa) \( \Leftrightarrow A \ge 0\). +) Phân thức xác định khi và chỉ khi mẫu thức khác 0. Lời giải chi tiết: ĐKXĐ: \(\left\{ \begin{array}{l}4 - 3x \ge 0\\x + 2 \ge 0\\\sqrt {x + 2} \ne 0\\x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le \dfrac{4}{3}\\x \ge - 2\\x \ne - 2\\x \ne - 1\end{array} \right. \Leftrightarrow - 2 < x \le \dfrac{4}{3},\,\,x \ne - 1\). Chọn C. Câu hỏi 9 :
Phương pháp giải: Lời giải chi tiết:
Câu hỏi 10 :
Phương pháp giải: Lời giải chi tiết:
Câu hỏi 11 :
Phương pháp giải: Lời giải chi tiết:
Câu hỏi 12 :
Phương pháp giải: Lời giải chi tiết:
Câu hỏi 13 :
Phương pháp giải: Lời giải chi tiết:
Câu hỏi 14 : Số nghiệm của phương trình \(\left( {\sqrt 5 - 1} \right){x^4} + 5{x^2} + 7\left( {1 - \sqrt 2 } \right) = 0\) là:
Đáp án: C Phương pháp giải: Giải phương trình trùng phương bằng cách đặt \({x^2} = t\,\,\left( {t \ge 0} \right)\) Lời giải chi tiết: Đặt \({x^2} = t\,\,\left( {t \ge 0} \right)\) khi đó phương trình trở thành \(\left( {\sqrt 5 - 1} \right){t^2} + 5t + 7\left( {1 - \sqrt 2 } \right) = 0\,\,\left( * \right)\) Sử dụng MTCT ta tính được phương trình (*) chỉ có 1 nghiệm thỏa mãn t > 0. Với 1 nghiệm t > 0 ta tìm được 2 nghiệm \(x = \pm \sqrt t .\) Vậy phương trình ban đầu có 2 nghiệm. Chọn C. Câu hỏi 15 : Nếu hai số có tổng bằng – 13 và tích bằng 36 thì số lớn là:
Đáp án: C Phương pháp giải: Hai số có tổng bằng S và tích bằng P là nghiệm của phương trình \({X^2} - SX + P = 0.\) Lời giải chi tiết: Hai số cần tìm là nghiệm của phương trình \({X^2} + 13X + 36 = 0 \Leftrightarrow \left[ \begin{array}{l}X = - 4\\X = - 9\end{array} \right. \Rightarrow \)Số lớn là - 4. Chọn C. Câu hỏi 16 : Tổng các nghiệm của phương trình \(\sqrt 2 {x^2} - 4x + 4 - \sqrt 2 = 0\) bằng:
Đáp án: D Phương pháp giải: Sử dụng định lí Vi-et để tính tổng các nghiệm của phương trình bậc hai. Lời giải chi tiết: Khi phương trình trên có nghiệm thì theo định lí Vi-et ta có: \({x_1} + {x_2} = - \frac{b}{a} = \frac{4}{{\sqrt 2 }} = 2\sqrt 2 .\) Chọn D. Câu hỏi 17 : Gọi \({x_1},{x_2}\) là các nghiệm của phương trình \(4{x^2} - 7x + 1 = 0.\) Khi đó giá trị biểu thức \(M = x_1^2 + x_2^2\) là:
Đáp án: C Phương pháp giải: Phân tích \(M = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\) sau đó áp dụng định lí Vi-et \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right.\) Lời giải chi tiết: Ta có \(\Delta = {7^2} - 4.4.\left( { - 1} \right) > 0 \Rightarrow \) phương trình có 2 nghiệm phân biệt \({x_1},{x_2}\) Theo định lí Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a} = \frac{7}{4}\\{x_1}{x_2} = \frac{c}{a} = \frac{1}{4}\end{array} \right.\) Ta có: \(M = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {\left( {\frac{7}{4}} \right)^2} - 2\left( { \frac{1}{4}} \right) = \frac{{41}}{{16}}.\) Chọn C. Câu hỏi 18 : Phương trình x2 – m x + 15 = 0 có một nghiệm x1 = 5 thì m và nghiệm x2 còn lại là :
Đáp án: D Phương pháp giải: \(x = {x_0}\) là nghiệm của phương trình \(f\left( x \right) = 0\) thì \(f\left( {{x_0}} \right) = 0.\) Lời giải chi tiết: Vì \({x_1} = 5\) là 1 nghiệm của phương trình \( \Rightarrow 25 - 5m + 15 = 0 \Leftrightarrow 5m = 40 \Leftrightarrow m = 8.\) Khi đó phương trình trở thành: \({x^2} - 8x + 15 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = 3\end{array} \right..\) Chọn D Câu hỏi 19 : Nghiệm của phương trình \(x + \frac{1}{{x - 1}} = \frac{{2x - 1}}{{x - 1}}\)
Đáp án: B Phương pháp giải: - Tìm TXĐ - Quy đồng mẫu thức các phân thức. - Khử mẫu. - Giải phương trình tìm nghiệm. Lời giải chi tiết: TXĐ: \(D = R\backslash \left\{ 1 \right\}.\) \(\begin{array}{l}x + \frac{1}{{x - 1}} = \frac{{2x - 1}}{{x - 1}}\\ \Rightarrow x\left( {x - 1} \right) + 1 = 2x - 1\\ \Leftrightarrow {x^2} - x + 1 - 2x + 1 = 0\\ \Leftrightarrow {x^2} - 3x + 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {tm} \right)\\x = 1\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy nghiệm của phương trình là x = 2. Chọn B Câu hỏi 20 : Tập nghiệm của phương trình \(\left( {{x^2} - x - 2} \right)\sqrt {x - 1} = 0\) là:
Đáp án: B Phương pháp giải: Tìm TXĐ của phương trình sau đó giải phương trình tích. Lời giải chi tiết: TXĐ:\(x \ge 1\) \(\left( {{x^2} - x - 2} \right)\sqrt {x - 1} = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} - x - 2 = 0\\\sqrt {x - 1} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 1\\x = 1\end{array} \right..\) Kết hợp điều kiện xác định ta có tập nghiệm của phương trình là \(\left\{ {1;2} \right\}\). Chọn B. Câu hỏi 21 : Tích các nghiệm của phương trình: \(\sqrt{x+3}-\sqrt{7-x}=\sqrt{2x-8}\) là:
Đáp án: C Phương pháp giải: + Phương trình có dạng: \(\sqrt{f(x)}-\sqrt{g(x)}=\sqrt{h(x)}\), điều kiện là \(\left\{ \begin{align} & f(x)\ge 0 \\ & g(x)\ge 0 \\ & h(x)\ge 0 \\\end{align} \right.\) + Khi đó: \(\sqrt{f(x)}=\sqrt{h(x)}+\sqrt{g(x)}\Leftrightarrow {{\left( \sqrt{f(x)} \right)}^{2}}={{\left( \sqrt{h(x)}+\sqrt{g(x)} \right)}^{2}}\), giải phương trình ta tìm được x Lời giải chi tiết: Điều kiện: \(\left\{ \begin{array}{l}x + 3 \ge 0\\7 - x \ge 0\\2{\rm{x}} - 8 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 3\\x \le 7\\x \ge 4\end{array} \right. \Leftrightarrow 4 \le x \le 7\) Khi đó: \(\sqrt{x+3}-\sqrt{7-x}=\sqrt{2x-8}\Leftrightarrow \sqrt{x+3}=\sqrt{2x-8}+\sqrt{7-x}\) \(\begin{array}{l} \Leftrightarrow x + 3 = 2{\rm{x}} - 8 + 7 - x + 2\sqrt {(2{\rm{x}} - 8)(7 - x)} \\ \Leftrightarrow 2\sqrt {(2{\rm{x}} - 8)(7 - x)} = 4\\ \Leftrightarrow - 2{{\rm{x}}^2} + 22{\rm{x}} - 56 = 4\\ \Leftrightarrow - {x^2} + 11{\rm{x}} - 30 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 5\,\,\,\left( {tm} \right)\\x = 6\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) \(\Rightarrow\) Tích của 2 nghiệm bằng 30 Chọn C. Câu hỏi 22 : Số nghiệm của phương trình \(\left( {{x^4} - 11{x^2} + 18} \right)\sqrt {x + 2} = 0\) là:
Đáp án: D Phương pháp giải: Tìm TXĐ của phương trình sau đó giải phương trình tích. Lời giải chi tiết: - TXĐ: \(x \ge - 2.\) \(\begin{array}{l}\left( {{x^4} - 11{x^2} + 18} \right)\sqrt {x + 2} = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^4} - 11{x^2} + 18 = 0\\\sqrt {x + 2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left( {{x^2} - 9} \right)\left( {{x^2} - 2} \right) = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} - 9 = 0\\{x^2} - 2 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \pm 3\\x = \pm \sqrt 2 \\x = - 2\end{array} \right..\end{array}\) Kết hợp điều kiện ta có \(\left[ \begin{array}{l}x = 3\\x = \pm \sqrt 2 \\x = - 2\end{array} \right.\) Vậy phương trình đã cho có 4 nghiệm. Chọn D. Câu hỏi 23 : Phương trình \({x^2} + 5x - 9 = 0\) có tổng bình phương hai nghiệm là:
Đáp án: C Phương pháp giải: Cách 1: Tính trực tiếp hai nghiệm của phương trình bậc hai rồi tính tổng bình phương của 2 nghiệm đó. Cách 2: Áp dụng định lí Vi-et: \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}.\) Lời giải chi tiết: Vì ac = -9 < 0 nên phương trình luôn có 2 nghiệm trái dấu. Gọi hai nghiệm của phương trình là \({x_1},{x_2}\). Theo định lí Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 5\\{x_1}{x_2} = - 9\end{array} \right.\) Ta có: \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {\left( { - 5} \right)^2} - 2.\left( { - 9} \right) = 25 + 18 = 43.\) Chọn C. Câu hỏi 24 : Tổng hai nghiệm của phương trình \(5\sqrt x + \dfrac{5}{{2\sqrt x }} = 2{\rm{x}} + \dfrac{1}{{2{\rm{x}}}} + 4\) là:
Đáp án: B Phương pháp giải: Đặt: \(\sqrt x + \dfrac{1}{{2\sqrt x }} = t\,\,(t \ge 0) \Leftrightarrow {\left( {\sqrt x + \dfrac{1}{{2\sqrt x }}} \right)^2} = {t^2}\) ta được phương trình bậc 2 ẩn t Lời giải chi tiết: Điều kiện: \(x > 0\) Ta có: \(5\sqrt x + \dfrac{5}{{2\sqrt x }} = 2{\rm{x}} + \dfrac{1}{{2{\rm{x}}}} + 4 \Leftrightarrow 5\left( {\sqrt x + \dfrac{1}{{2\sqrt x }}} \right) = 2\left( {{\rm{x}} + \dfrac{1}{{{\rm{4x}}}}} \right) + 4\) Đặt \(\sqrt x + \dfrac{1}{{2\sqrt x }} = t\,\,\,\left( {t > 0} \right) \Leftrightarrow {t^2} = x + \dfrac{1}{{4x}} + 1 \Leftrightarrow x + \dfrac{1}{{4x}} = {t^2} - 1\) Khi đó phương trình trở thành: \(5t = 2\left( {{t^2} - 1} \right) + 4 \Leftrightarrow 2{t^2} - 5t + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 2\,\,\,\left( {tm} \right)\\t = \dfrac{1}{2}\,\,\,\left( {tm} \right)\end{array} \right.\) +) Với \(t = \dfrac{1}{2} \Leftrightarrow x + \dfrac{1}{{4{\rm{x}}}} = - \dfrac{3}{4} \Leftrightarrow 4{{\rm{x}}^2}{\rm{ + 3x}} + 1 = 0\) (vô nghiệm) +) Với t = 2\( \Leftrightarrow x + \dfrac{1}{{4{\rm{x}}}} = 3 \Leftrightarrow 4{{\rm{x}}^2} - 12{\rm{x}} + 1 = 0\) Tổng 2 nghiệm của phương trình là: 3 Chọn B. Câu hỏi 25 : Cho phương trình \(2{{\rm{x}}^2} + 3{\rm{x}} - 14 = 2\sqrt[3]{{2{{\rm{x}}^2} + 3{\rm{x}} - 10}}\) . Giả sử x1, x2 là 2 nghiệm của phương trình. Tính giá trị biểu thức \(A = \sqrt {{x_1}^2 + {x_2}^2 - 4{{\rm{x}}_1}.{x_2}} \)
Đáp án: D Phương pháp giải: + Đặt \(t = \sqrt[3]{{2{{\rm{x}}^2} + 3{\rm{x}} - 10}}\) suy ra phương trình bậc 3 với ẩn t + Tính giá trị biểu thức A bằng cách sử dụng định lý Vi – et Lời giải chi tiết: Đặt \(t = \sqrt[3]{{2{{\rm{x}}^2} + 3{\rm{x}} - 10}} \Leftrightarrow {t^3} = 2{{\rm{x}}^2} + 3{\rm{x}} - 10 \Leftrightarrow {t^3} + 10 = 2{{\rm{x}}^2} + 3{\rm{x}}\) Khi đó phương trình trở thành: \({t^3} + 10 - 14 = 2t \Leftrightarrow {t^3} - 2t - 4 = 0\) \( \Leftrightarrow \left( {t - 2} \right)\left( {{t^2} + 2t + 2} \right) = 0 \Leftrightarrow t = 2\) (Vì \({t^2} + 2t + 2\) = 0 vô nghiệm) +) Với t = 2 \( \Leftrightarrow 2{{\rm{x}}^2} + 3x = 18 \Leftrightarrow 2{{\rm{x}}^2} + 3x - 18 = 0\,\,\left( * \right)\,\,\,\left( {tm} \right)\) Giả sử x1, x2 là hai nghiệm của phương trình (*) Theo Vi – et, ta có : \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{3}{2}\\{x_1}.{x_2} = - 9\end{array} \right.\) \( \Rightarrow A = \sqrt {{x_1}^2 + {x_2}^2 - 4{{\rm{x}}_1}{x_2}} = \sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 6{x_1}.{x_2}} = \sqrt {\dfrac{9}{4} + 54} = \sqrt {\dfrac{{225}}{4}} = \dfrac{{15}}{2}\) Chọn D. Câu hỏi 26 : Tập nghiệm của phương trình \(4{x^2} + 5{\rm{x}} = 2\sqrt {x + 2} - 4\) là:
Đáp án: A Phương pháp giải: + Đưa phương trình về dạng : \({A^2} + {B^2} = 0\) + Phương trình có nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\). Giải hệ phương trình ta tìm được x Lời giải chi tiết: Điều kiện: \(x + 2 \ge 0 \Leftrightarrow x \ge - 2\) Phương trình: \(4{x^2} + 5{\rm{x}} = 2\sqrt {x + 2} - 4 \Leftrightarrow 4{x^2} + 5x - 2\sqrt {x + 2} + 4 = 0\) \(\begin{array}{l} \Leftrightarrow \left( {4{x^2} + 4x + 1} \right) + \left( {x + 2 - 2\sqrt {x + 2} + 1} \right) = 0\\ \Leftrightarrow {\left( {2{\rm{x}} + 1} \right)^2} + {\left( {\sqrt {x + 2} - 1} \right)^2} = 0\end{array}\) Ta có:\({\left( {2{\rm{x}} + 1} \right)^2} \ge 0,{\left( {\sqrt {x + 2} - 1} \right)^2} \ge 0,\forall x \ge - 2\) Để \({\left( {2{\rm{x}} + 1} \right)^2} + {\left( {\sqrt {x + 2} - 1} \right)^2} = 0\) Thì: \(\left\{ \begin{array}{l}{\left( {2{\rm{x}} + 1} \right)^2} = 0\\{\left( {\sqrt {x + 2} - 1} \right)^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{\rm{x}} + 1 = 0\\\sqrt {x + 2} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \dfrac{1}{2}\\x = - 1\end{array} \right.\) (vô lý) Vậy phương trình vô nghiệm. Chọn A. Câu hỏi 27 : Số nghiệm nguyên của phương trình \(\sqrt{5\text{x}-3}+\sqrt{3\text{x}-1}=x-1\) là:
Đáp án: A Phương pháp giải: + Phương trình có dạng: \(\sqrt{f(x)}+\sqrt{g(x)}=h(x)\), điều kiện là \(\left\{ \begin{align} & f(x)\ge 0 \\ & g(x)\ge 0 \\ & h(x)\ge 0 \\\end{align} \right.\) + Khi đó: \({{\left( \sqrt{f(x)}+\sqrt{g(x)} \right)}^{2}}={{h}^{2}}(x)\), giải phương trình ta tìm được x Lời giải chi tiết: Điều kiện: \(\left\{ \begin{array}{l}5x - 3 \ge 0\\3x - 1 \ge 0\\x - 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{3}{5}\\x \ge \frac{1}{3}\\x \ge 1\end{array} \right. \Leftrightarrow x \ge 1\) Phương trình \(\Leftrightarrow 5\text{x}-3+3\text{x}-1+2\sqrt{(5\text{x}-3)(3\text{x}-1)}={{x}^{2}}-2\text{x}+1\) \(\Leftrightarrow 2\sqrt{(5\text{x}-3)(3\text{x}-1)}={{x}^{2}}-10\text{x}+5\) Điều kiện : \({{x}^{2}}-10\text{x}+5\ge 0\Leftrightarrow \left[ \begin{align} & x\ge 5+2\sqrt{5} \\& x\le 5-2\sqrt{5} \\\end{align} \right.\) Phương trình \(\begin{array}{l} \Leftrightarrow 4\left( {15{{\rm{x}}^2} - 14{\rm{x}} + 3} \right) = {\left( {{x^2} - 10{\rm{x}} + 5} \right)^2}\\ \Leftrightarrow 60{x^2} - 56x + 12 = {x^4} + 100{x^2} + 25 - 20{x^3} + 10{x^2} - 100x\\ \Leftrightarrow {x^4} - 20{{\rm{x}}^3} + 50{{\rm{x}}^2} - 44{\rm{x}} + 13 = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2}\left( {{x^2} - 18{\rm{x}} + 13} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(ktm)\\x = 9 \pm 2\sqrt {17} \notin Z\,\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy phương trình không có nghiệm nguyên. Chọn A Câu hỏi 28 : a) Tìm m để phương trình \({x^2} + 2x + m = 0\) có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa \(x_1^2 + x_2^2 = 6\). b) Giải phương trình: \(\sqrt {{x^2} + 2x - 6} = 2x - 3\).
Đáp án: A Phương pháp giải: a)Sử dụng hệ thức Vi-ét. b)\(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\). Lời giải chi tiết: a)Để phương trình \({x^2} + 2x + m = 0\) có 2 nghiệm phân biệt thì \(\Delta ' > 0 \Leftrightarrow 1 - m > 0 \Leftrightarrow m < 1\) Theo Vi – ét, ta có: \({x_1} + {x_2} = \frac{{ - 2}}{1} = - 2,\,\,\,{x_1}{x_2} = \frac{m}{1} = m\) Theo đề bài: \(x_1^2 + x_2^2 = 6 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 6 \Leftrightarrow {\left( { - 2} \right)^2} - 2m = 6 \Leftrightarrow 4 - 2m = 6 \Leftrightarrow 2m = - 2 \Leftrightarrow m = - 1\) (thỏa mãn) Kết luận: \(m = - 1\). b) \(\begin{array}{l}\sqrt {{x^2} + 2x - 6} = 2x - 3 \Leftrightarrow \left\{ \begin{array}{l}2x - 3 \ge 0\\{x^2} + 2x - 6 = {\left( {2x - 3} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{3}{2}\\{x^2} + 2x - 6 = 4{x^2} - 12x + 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{3}{2}\\3{x^2} - 14x + 15 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \frac{5}{3}\end{array} \right.\,\,\left( {tm} \right)\end{array}\) Vậy, phương trình đã cho có tập nghiệm \(S = \left\{ {3;\frac{5}{3}} \right\}\). Câu hỏi 29 : Số nghiệm nguyên của phương trình: \(\sqrt {x - 3} + 5 = \sqrt {7 - x} + x\) là:
Đáp án: A Phương pháp giải: Sử dụng biểu thức liên hợp. Lời giải chi tiết:
ĐKXĐ: \(\left\{ \begin{array}{l}x - 3 \ge 0\\7 - x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\x \le 7\end{array} \right. \Leftrightarrow 3 \le x \le 7 \Rightarrow \)Tập xác định \(D = \left[ {3;7} \right]\) \(\begin{array}{l}\sqrt {x - 3} + 5 = \sqrt {7 - x} + x \Leftrightarrow \sqrt {x - 3} - \sqrt {7 - x} = x - 5 \Leftrightarrow \frac{{\left( {\sqrt {x - 3} - \sqrt {7 - x} } \right)\left( {\sqrt {x - 3} + \sqrt {7 - x} } \right)}}{{\sqrt {x - 3} + \sqrt {7 - x} }} = x - 5\\ \Leftrightarrow \frac{{2x - 10}}{{\sqrt {x - 3} + \sqrt {7 - x} }} = x - 5 \Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\\frac{2}{{\sqrt {x - 3} + \sqrt {7 - x} }} = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\,\,(TM)\\\sqrt {x - 3} + \sqrt {7 - x} = 2\,\,(1)\end{array} \right.\end{array}\), \(\left( 1 \right) \Leftrightarrow x - 3 + 2\sqrt {\left( {x - 3} \right)\left( {7 - x} \right)} + 7 - x = 4 \Leftrightarrow 2\sqrt {\left( {x - 3} \right)\left( {7 - x} \right)} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 7\end{array} \right.\,\,\,\,\left( {TM} \right)\) Vậy phương trình đã cho có 3 nghiệm nguyên là \(x = 3,\,\,x = 5,\,\,x = 7\). Chọn: A Câu hỏi 30 : Tìm m để phương trình \({x^2} - \left( {2m + 1} \right)x + {m^2} + 1 = 0\) có 2 nghiệm \({x_1};{x_2}\) thỏa mãn \({x_2} = 2{x_1}\)
Đáp án: A Phương pháp giải: +) Tìm điều kiện để phương trình có 2 nghiệm. +) Sử dụng hệ thức Vi-ét. Lời giải chi tiết: Ta có: \(\begin{gathered} \Delta = {\left( {2m + 1} \right)^2} - 4\left( {{m^2} + 1} \right) \hfill \\ \Delta = 4{m^2} + 4m + 1 - 4{m^2} - 4 = 4m - 3 \hfill \\ \end{gathered} \) Để phương trình có 2 nghiệm \({x_1};{x_2} \Leftrightarrow \Delta \geqslant 0 \Leftrightarrow 4m - 3 \geqslant 0 \Leftrightarrow m \geqslant \frac{3}{4}\) Theo hệ thức Vi-ét ta có: \(\left\{ \begin{gathered} {x_1} + {x_2} = 2m + 1 \hfill \\ {x_1}{x_2} = {m^2} + 1 \hfill \\ \end{gathered} \right.\) Để 2 nghiệm \({x_1};{x_2}\) thỏa mãn \({x_2} = 2{x_1}\) ta có: \(\left\{ \begin{gathered} {x_1} + {x_2} = 2m + 1 \hfill \\ {x_1}{x_2} = {m^2} + 1 \hfill \\ {x_2} = 2{x_1} \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} 3{x_1} = 2m + 1 \hfill \\ 2x_1^2 = {m^2} + 1 \hfill \\ {x_2} = 2{x_1} \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} {x_1} = \frac{{2m + 1}}{3} \hfill \\ {x_2} = \frac{{2\left( {2m + 1} \right)}}{3} \hfill \\ 2.\frac{{{{\left( {2m + 1} \right)}^2}}}{9} = {m^2} + 1\,\,\left( * \right) \hfill \\ \end{gathered} \right.\) Giải (*): \(\frac{{2{{\left( {2m + 1} \right)}^2}}}{9} = {m^2} + 1 \Leftrightarrow 2\left( {4{m^2} + 4m + 1} \right) = 9\left( {{m^2} + 1} \right) \Leftrightarrow {m^2} - 8m + 7 = 0 \Leftrightarrow \left[ \begin{gathered} m = 1 \hfill \\ m = 7 \hfill \\ \end{gathered} \right.\,\,\left( {tm} \right)\) Vậy \(m = 1;\,\,m = 7\) Câu hỏi 31 : Cho phương trình \(\frac{{3m\left( {x - 1} \right)}}{{x + 1}} = 5m + 1\). Khẳng định nào dưới đây đúng?
Đáp án: C Phương pháp giải: Xét phương trình dạng \(a\,x = b\) (1): +) Nếu \(a \ne 0\) thì (1) có nghiệm duy nhất \(x = \frac{b}{a}\) +) Nếu \(a = b = 0\) thì (1) có vô số nghiệm +) Nếu \(a = 0,\,\,b \ne 0\) thì (1) vô nghiệm. Lời giải chi tiết:
ĐKXĐ: \(x \ne - 1\) \(\begin{array}{l}\frac{{3m\left( {x - 1} \right)}}{{x + 1}} = 5m + 1\,\,\,(*) \Leftrightarrow 3m\left( {x - 1} \right) = \left( {5m + 1} \right)\left( {x + 1} \right) \Leftrightarrow 3mx - 3m = 5mx + 5m + x + 1\\ \Leftrightarrow \left( {2m + 1} \right)x = - 8m - 1\,\,(2*)\end{array}\) +) TH1: \(2m + 1 = 0 \Leftrightarrow m = - \frac{1}{2}\): \(\left( {2*} \right) \Leftrightarrow 0x = - \frac{3}{4}\) (vô nghiệm) \( \Rightarrow \) Phương trình (*) vô nghiệm. +) TH2: \(2m + 1 \ne 0 \Leftrightarrow m \ne - \frac{1}{2}\): \(\left( {2*} \right) \Leftrightarrow x = \frac{{ - 8m - 1}}{{2m + 1}}\) Xét \(\frac{{ - 8m - 1}}{{2m + 1}} = - 1 \Leftrightarrow 8m + 1 = 2m + 1 \Leftrightarrow m = 0\) \( \Rightarrow \) Với \(m = 0\): phương trình (*) vô nghiệm; với \(m \ne 0\), phương trình (*) có nghiệm duy nhất \(x = \frac{{ - 8m - 1}}{{2m + 1}}\). Chọn: C Câu hỏi 32 : Cho phương trình \(\left| {x - 3m + 1} \right| = \left| {\left( {m + 1} \right)x - 3} \right|\). Khẳng định nào dưới đây đúng?
Đáp án: B Phương pháp giải: Xét phương trình dạng \(a\,x = b\) (1): +) Nếu \(a \ne 0\) thì (1) có nghiệm duy nhất \(x = \frac{b}{a}\) +) Nếu \(a = b = 0\) thì (1) có vô số nghiệm +) Nếu \(a = 0,\,\,b \ne 0\) thì (1) vô nghiệm. Lời giải chi tiết:
\(\left| {x - 3m + 1} \right| = \left| {\left( {m + 1} \right)x - 3} \right|\,\,\,\,\,\,(*)\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x - 3m + 1 = \left( {m + 1} \right)x - 3\\x - 3m + 1 = - \left( {m + 1} \right)x + 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}mx = - 3m + 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\\left( {m + 2} \right)x = 3m + 2\,\,\,\,\,\,(2)\end{array} \right.\) +) \(m = 0\): \( - 3m + 4 = 4 \ne 0 \Rightarrow \) Phương trình (1) vô nghiệm \((2) \Leftrightarrow 2x = 2 \Leftrightarrow x = 1\): Phương trình (2) có nghiệm duy nhất \(x = 1\) Vậy, với \(m = 0\) phương trình đã cho có nghiệm duy nhất \(x = 1\). +) \(m = - 2\): \((1) \Leftrightarrow - 2x = 10 \Leftrightarrow x = - 5\): Phương trình (1) có nghiệm duy nhất \(x = - 5\) \((2) \Leftrightarrow 0x = - 4\): Vô nghiệm Vậy, với \(m = - 2\) phương trình đã cho có nghiệm duy nhất \(x = - 5\). +) \(m \ne 0\) và \(m \ne - 2\) \(\left( 1 \right) \Leftrightarrow x = \frac{{ - 3m + 4}}{m};\,\,\,\,\,\left( 2 \right) \Leftrightarrow \frac{{3m + 2}}{{m + 2}}\) Xét \(\frac{{ - 3m + 4}}{m} = \frac{{3m + 2}}{{m + 2}}\)\(\begin{array}{l} \Leftrightarrow \left( { - 3m + 4} \right)\left( {m + 2} \right) = \left( {3m + 2} \right)m \Leftrightarrow - 3{m^2} - 2m + 8 = 3{m^2} + 2m \Leftrightarrow 6{m^2} + 4m - 8 = 0 \Leftrightarrow 3{m^2} + 2m - 4 = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = \frac{{ - 1 + \sqrt {13} }}{3}\\m = \frac{{ - 1 - \sqrt {13} }}{3}\end{array} \right.\end{array}\)\( \Rightarrow \frac{{3m - 4}}{m} \ne \frac{{3m + 2}}{{m + 2}},\,\,\forall m \ne 0,\,m \ne - 2,\,m \ne \frac{{ - 1 \pm \sqrt {13} }}{3}\) Vậy, với \(m \ne 0\), \(m \ne - 2\) và \(\,m \ne \frac{{ - 1 \pm \sqrt {13} }}{3}\) phương trình đã cho có 2 nghiệm phân biệt. Với \(\,m = \frac{{ - 1 \pm \sqrt {13} }}{3}\), phương trình có nghiệm duy nhất. Chọn: B Câu hỏi 33 : Gọi n là số các giá trị của tham số m để phương trình \(\frac{{\left( {x + 1} \right)\left( {mx + 2} \right)}}{{x - 2}} = 0\) có nghiệm duy nhất. Khi đó n là :
Đáp án: D Phương pháp giải: Giải phương trình tích. TH1 : \(m = 0\) TH2: \(m \ne 0\), phương trình có nghiệm duy nhất khi phương trình tử có nghiệm kép hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm không thỏa mãn ĐK của bài toán. Lời giải chi tiết: ĐK : \(x \ne 2\) \(\frac{{\left( {x + 1} \right)\left( {mx + 2} \right)}}{{x - 2}} = 0 \Leftrightarrow \left[ \begin{gathered} x = - 1\,\,\,\left( {tm} \right) \hfill \\ mx + 2 = 0\,\,\,\left( * \right) \hfill \\ \end{gathered} \right.\) Giải (*) TH1 : \(m = 0 \Rightarrow 0x + 2 = 0\) (Vô nghiệm) \( \Rightarrow \) Phương trình ban đầu có nghiệm duy nhất \(x = - 1\). \( \Rightarrow m = 0\) thỏa mãn. TH2 : \(m \ne 0 \Rightarrow \left( * \right) \Leftrightarrow x = \frac{{ - 2}}{m}\) Để phương trình ban đầu có nghiệm duy nhất \( \Leftrightarrow \left[ \begin{gathered} -\frac{2}{m} = - 1 \hfill \\ - \frac{2}{m} = 2 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m = 2 \hfill \\ m = - 1 \hfill \\ \end{gathered} \right.\) Vậy \(m \in \left\{ {0; - 1;2} \right\}\). Khi đó \(n = 3\). Chọn đáp án D. Câu hỏi 34 : Xác định \(m\) để phương trình \({x^2} + 1 = mx\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa \({x_1} - {x_2} = 1\) (giả sử \({x_1} > {x_2}\)).
Đáp án: A Phương pháp giải: Phương trình có 2 nghiệm phân biệt \( \Leftrightarrow \Delta > 0\). Sử dụng hệ thức Vi-ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right.\). Lời giải chi tiết:
\({x^2} + 1 = mx \Leftrightarrow {x^2} - mx + 1 = 0\) Để phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta = {m^2} - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 2\\m < - 2\end{array} \right.\) Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = 1\end{array} \right.\) Ta có: \(\begin{array}{l}{x_1} - {x_2} = 1 \Rightarrow {\left( {{x_1} - {x_2}} \right)^2} = 1 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 1\\ \Leftrightarrow {m^2} - 4 = 1 \Leftrightarrow {m^2} = 5 \Leftrightarrow m = \pm \sqrt 5 \,\,\left( {tm} \right)\end{array}\) Vậy \(m = \pm \sqrt 5 \). Câu hỏi 35 : Tìm tất cả các giá trị của m để phương trình \({x^2} - \left( {2m + 1} \right)x + {m^2} + 2 = 0\) có hai nghiệm \({x_1};{x_2}\) phân biệt sao cho \({x_1}\left( {{x_2} - 2{x_1}} \right) + {x_2}\left( {{x_1} - 2{x_2}} \right) + 14 = 0\).
Đáp án: A Phương pháp giải: +) Tìm điều kiện để phương trình có 2 nghiệm phân biệt. +) Áp dụng định lí Vi-ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\) Lời giải chi tiết: Để phương trình có 2 nghiệm phân biệt \({x_1};{x_2}\)\( \Leftrightarrow \Delta > 0\) \( \Leftrightarrow {\left( {2m + 1} \right)^2} - 4\left( {{m^2} + 2} \right) > 0 \Leftrightarrow 4{m^2} + 4m + 1 - 4{m^2} - 8 > 0 \Leftrightarrow 4m - 7 > 0 \Leftrightarrow m > \dfrac{7}{4}\). Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = {m^2} + 2\end{array} \right.\) \(\begin{array}{l}\,\,\,\,\,{x_1}\left( {{x_2} - 2{x_1}} \right) + {x_2}\left( {{x_1} - 2{x_2}} \right) + 14 = 0\\ \Leftrightarrow {x_1}{x_2} - 2x_1^2 + {x_1}{x_2} - 2x_2^2 + 14 = 0\\ \Leftrightarrow 2{x_1}{x_2} - 2\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right] + 14 = 0\\ \Leftrightarrow - 2{\left( {{x_1} + {x_2}} \right)^2} + 6{x_1}{x_2} + 14 = 0\\ \Leftrightarrow - 2{\left( {2m + 1} \right)^2} + 6\left( {{m^2} + 2} \right) + 14 = 0\\ \Leftrightarrow - 8{m^2} - 8m - 2 + 6{m^2} + 12 + 14 = 0\\ \Leftrightarrow - 2{m^2} - 8m + 24 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 2\,\,\,\,\,\,\left( {tm} \right)\\m = - 6\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy \(m = 2.\) Câu hỏi 36 : Số nghiệm của phương trình \({x^2} + 3x + 1 = \left( {x + 3} \right)\sqrt {{x^2} + 1} \) là
Đáp án: D Phương pháp giải: Đặt \(\sqrt {{x^2} + 1} = t\). Lời giải chi tiết: \({x^2} + 3x + 1 = \left( {x + 3} \right)\sqrt {{x^2} + 1} \,\,\,\left( {D = R} \right)\). Đặt \(\sqrt {{x^2} + 1} = t\), \(t \ge 1\), phương trình trở thành: \({t^2} + 3x = \left( {x + 3} \right)t \Leftrightarrow {t^2} + 3x = xt + 3t \Leftrightarrow t\left( {x - t} \right) + 3\left( {x - t} \right) = 0 \Leftrightarrow \left( {x - t} \right)\left( {t - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = t\\t = 3\end{array} \right.\) +) \(x = t \Rightarrow x = \sqrt {{x^2} + 1} \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} = {x^2} + 1\end{array} \right. \Leftrightarrow x \in \emptyset \) +) \(t = 3 \Rightarrow \sqrt {{x^2} + 1} = 3 \Leftrightarrow {x^2} = 8 \Leftrightarrow x = \pm 2\sqrt 2 \) \( \Rightarrow \) Số nghiệm của phương trình là 2. Chọn: D Câu hỏi 37 : Giải phương trình \(\sqrt {2{x^2} - 5x + 2} = x - 2\)
Đáp án: B Phương pháp giải: \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\) Lời giải chi tiết: \(\sqrt {2{x^2} - 5x + 2} = x - 2 \Leftrightarrow \left\{ \begin{array}{l}x - 2 \ge 0\\2{x^2} - 5x + 2 = {x^2} - 4x + 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\{x^2} - x - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\\left[ \begin{array}{l}x = 2\\x = - 1\end{array} \right.\end{array} \right. \Leftrightarrow x = 2\) Vậy phương trình có nghiệm duy nhất \(x = 2\). Câu hỏi 38 : Tìm m để phương trình \(\frac{{2\left( {2 - 2m - x} \right)}}{{x + 1}} = x - 2m\) có 2 nghiệm phân biệt ?
Đáp án: B Phương pháp giải: +) Tìm ĐKXĐ. +) Quy đồng bỏ mẫu, đưa phương trình về dạng phương trình bậc hai. +) Tìm điều kiện để phương trình bậc hai đó có 2 nghiệm phân biệt thỏa mãn ĐKXĐ. Lời giải chi tiết: ĐK : \(x \ne - 1\) \(\begin{array}{l}pt \Leftrightarrow 4 - 4m - 2x = {x^2} - 2mx + x - 2m\\ \Leftrightarrow {x^2} + \left( {3 - 2m} \right)x + 2m - 4 = 0\,\,\left( * \right)\end{array}\) Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) có 2 nghiệm phân biệt khác 1. \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{\left( {3 - 2m} \right)^2} - 4\left( {2m - 4} \right) > 0\\1 - 3 + 2m + 2m - 4 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 20m + 25 > 0\\4m - 6 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( {2m - 5} \right)^2} > 0\\m \ne \frac{3}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m - 5 \ne 0\\m \ne \frac{3}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne \frac{5}{2}\\m \ne \frac{3}{2}\end{array} \right.\end{array}\) Vậy \(m \ne \frac{5}{2}\) và \(m \ne \frac{3}{2}\). Chọn đáp án B. Câu hỏi 39 : Tìm m để parabol \(\left( P \right):\,\,y = {x^2} - 2\left( {m + 1} \right)x + {m^2} - 3\) cắt trục hoành tại 2 điểm phân biệt có hoành độ \({x_1};{x_2}\) sao cho \({x_1}{x_2} = 1\).
Đáp án: A Phương pháp giải: +) Xét phương trình hoành độ giao điểm, tìm điều kiện để phương trình hoành độ giao điểm có 2 nghiệm phân biệt. +) Sử dụng hệ thức Vi-ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right.\). Lời giải chi tiết: Xét phương trình hoành độ giao điểm: \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 3 = 0\,\,\left( * \right)\). Để (P) cắt trục hoành tại 2 điểm phân biệt có hoành độ \({x_1};{x_2}\)thì phương trình (*) có 2 nghiệm phân biệt. Ta có \(\Delta ' = {\left( {m + 1} \right)^2} - {m^2} + 3 = 2m + 4 > 0 \Leftrightarrow m > - 2\). Khi đó theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 2\\{x_1}{x_2} = {m^2} - 3\end{array} \right.\) Theo đề bài ta có \({x_1}{x_2} = 1 \Leftrightarrow {m^2} - 3 = 1 \Leftrightarrow \left[ \begin{array}{l}m = 2\,\,\left( {tm} \right)\\m = - 2\,\,\left( {ktm} \right)\end{array} \right.\) Chọn đáp án A. Câu hỏi 40 : Một xe hơi khởi hành từ Krông Năng đi đến Nha Trang cách nhau \({\rm{175}}\)km. Khi về xe tăng vận tốc trung bình hơn vận tốc trung bình lúc đi là \(20\)km/giờ. Biết rằng thời gian dùng để đi và về là \(6\)giờ; vận tốc trung bình lúc đi là:
Đáp án: D Phương pháp giải: Giải bài toán bằng cách lập phương trình. Lời giải chi tiết: Gọi vận tốc trung bình lúc đi là x (km/h) \(\left( {x > 0} \right)\) thì vận tốc trung bình lúc về là \(x + 20\,\,\left( {km/h} \right)\). Thời gian lúc đi và lúc về lần lượt là \(\dfrac{{175}}{x};\dfrac{{175}}{{x + 20}}\) (h). Vì thời gian dùng để đi và về là 6h nên ta có phương trình: \(\dfrac{{175}}{x} + \dfrac{{175}}{{x + 20}} = 6\) \( \Leftrightarrow 175\left( {x + 20} \right) + 175x = 6x\left( {x + 20} \right) \Leftrightarrow 6{x^2} - 230x - 3500 = 0 \Leftrightarrow x = 50\). Vậy vận tốc trung bình lúc đi là 50 km/h. Chọn D. Câu hỏi 41 : Tìm \(m\) để phương trình \(m{x^2}--2\left( {m + 1} \right)x + m + 1 = 0\) vô nghiệm.
Đáp án: A Phương pháp giải: TH1: \(m = 0\), thay vào tìm nghiệm của phương trình. TH2: \(m \ne 0\), phương trình vô nghiệm \( \Leftrightarrow \Delta ' < 0\). Lời giải chi tiết: TH1: \(m = 0\), phương trình trở thành \( - 2x + 1 = 0 \Leftrightarrow x = \dfrac{1}{2}\). Suy ra \(m = 0\) không thỏa mãn. TH2: \(m \ne 0\). Khi đó phương trình vô nghiệm \( \Leftrightarrow \Delta ' < 0\) \( \Leftrightarrow {\left( {m + 1} \right)^2} - m\left( {m + 1} \right) < 0 \Leftrightarrow {m^2} + 2m + 1 - {m^2} - m = m + 1 < 0 \Leftrightarrow m < - 1\). Chọn A. Câu hỏi 42 : Tìm tất cả các giá trị của m để phương trình \({x^2} - \left( {m + 1} \right)x + m = 0\) có hai nghiệm phân biệt và nghiệm này bằng một nửa nghiệm kia.
Đáp án: C Phương pháp giải: Phương trình bậc 2 có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0\). Kết hợp với hệ thức Vi-ét và dữ kiện đề bài để tìm m. Lời giải chi tiết: \({x^2} - \left( {m + 1} \right)x + m = 0\) (1) Có : \(\Delta = {\left( {m + 1} \right)^2} - 4m = {\left( {m - 1} \right)^2}\) Để phương trình (1) có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0 \Leftrightarrow m - 1 \ne 0 \Leftrightarrow m \ne 1\) Gọi \({x_1} > {x_2}\) là 2 nghiệm của (1) Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 1\\{x_1}.{x_2} = m\end{array} \right.\) Mặt khác theo đề bài: \({x_1} = 2{x_2} \Rightarrow \left\{ \begin{array}{l}2{x_2} + {x_2} = m + 1\\2{x_2}.{x_2} = m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = \frac{{m + 1}}{3}\\2{x_2}^2 = m\end{array} \right.\) \( \Rightarrow 2.\frac{{{{\left( {m + 1} \right)}^2}}}{9} = m \Leftrightarrow 2{m^2} + 4m + 2 = 9m \Leftrightarrow 2{m^2} - 5m + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 2\,\,\,\left( {tm} \right)\\m = \frac{1}{2}\,\,\,\left( {tm} \right)\end{array} \right.\) Chọn C. Câu hỏi 43 : Tìm tất cả các số thực m để phương trình \(2{x^2} - 4x + 1 + {m^2} = 0\) có hai nghiệm phân biệt.
Đáp án: A Phương pháp giải: Phương trình \(a{x^2} + bx + c = 0\,\,\,\,(a \ne 0)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0\) Lời giải chi tiết: Phương trình \(2{x^2} - 4x + 1 + {m^2} = 0\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\) \( \Leftrightarrow {2^2} - 2\left( {1 + {m^2}} \right) > 0 \Leftrightarrow 2{m^2} - 2 < 0 \Leftrightarrow {m^2} < 1 \Leftrightarrow - 1 < m < 1\) Chọn A. Câu hỏi 44 : Giải phương trình \(\left| {3x + 1} \right| = x + 3\) ta được số nghiệm của phương trình là:
Đáp án: C Phương pháp giải: Giải phương trình chứa dấu giá trị tuyệt đối và đếm số nghiệm. Lời giải chi tiết: \(\left| {3x + 1} \right| = x + 3 \Leftrightarrow \left\{ \begin{array}{l}x + 3 \ge 0\\9{x^2} + 6x + 1 = {x^2} + 6x + 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 3\\{x^2} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 3\\\left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\) Vậy phương trình có 2 nghiệm. Chọn C. Câu hỏi 45 : Tất cả giá trị của a để phương trình \(2x - 1 = 4 + 5a\) (với a là tham số) có nghiệm dương là
Đáp án: B Phương pháp giải: Giải phương trình và biện luận. Lời giải chi tiết: \(2x - 1 = 4 + 5a \Leftrightarrow 2x = 5a + 5 \Leftrightarrow x = \frac{{5a + 5}}{2}\) Để phương trình có nghiệm dương \( \Leftrightarrow \frac{{5a + 5}}{2} > 0 \Leftrightarrow 5a + 5 > 0 \Leftrightarrow a > - 1\) Chọn B. Câu hỏi 46 : Cho phương trình \({x^2} - 4x + 1 = 0\) có 2 nghiệm \({x_1},{x_2}\). Tính giá trị biểu thức \(P = {x_1} + {x_2} + {x_1}{x_2}\).
Đáp án: D Phương pháp giải: Áp dụng hệ thức Vi-ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right..\) Lời giải chi tiết: Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 4\\{x_1}.{x_2} = 1\end{array} \right.\) \(P = {x_1} + {x_2} + {x_1}{x_2} = 4 + 1 = 5\) Chọn D. Câu hỏi 47 : Tập nghiệm của phương trình \(\left| {3x - 1} \right| = 2\) là
Đáp án: A Phương pháp giải: \(\left| {f\left( x \right)} \right| = a > 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a\\f\left( x \right) = - a\end{array} \right.\) Lời giải chi tiết: \(\left| {3x - 1} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}3x - 1 = 2\\3x - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \frac{{ - 1}}{3}\end{array} \right.\) Vậy phương trình có tập nghiệm: \(S = \left\{ { - \frac{1}{3};\;1} \right\}.\) Chọn A. Câu hỏi 48 : Tập nghiệm của phương trình \(\left| {\left| {x - 1} \right| - 2} \right| = 4\) là S. Vậy S là
Đáp án: C Phương pháp giải: \(\left| {f\left( x \right)} \right| = a > 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a\\f\left( x \right) = - a\end{array} \right.\) Lời giải chi tiết: \(\left| {\left| {x - 1} \right| - 2} \right| = 4 \Leftrightarrow \left[ \begin{array}{l}\left| {x - 1} \right| - 2 = 4\\\left| {x - 1} \right| - 2 = - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left| {x - 1} \right| = 6\\\left| {x - 1} \right| = - 2\,\,(VN)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x - 1 = 6\\x - 1 = - 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 7\\x = - 5\end{array} \right.\) Vậy phương trình có tập nghiệm: \(S = \left\{ {7; - 5} \right\}.\) Chọn C. Câu hỏi 49 : Giải phương trình sau: \(\sqrt {2x + 1} - \sqrt {3x - 8} = 1\)
Đáp án: A Phương pháp giải: Bình phương hai vế không âm: \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\) Lời giải chi tiết: Giải phương trình sau: \(\sqrt {2x + 1} - \sqrt {3x - 8} = 1\) Điều kiện: \(\left\{ \begin{array}{l}3x - 8 \ge 0\\2x + 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{8}{3}\\x \ge - \frac{1}{2}\end{array} \right. \Leftrightarrow x \ge \frac{8}{3}.\) \(\begin{array}{l}Pt \Leftrightarrow \sqrt {2x + 1} = 1 + \sqrt {3x - 8} \Leftrightarrow 2x + 1 = 1 + 2\sqrt {3x - 8} + 3x - 8\\ \Leftrightarrow 2\sqrt {3x - 8} = 8 - x \Leftrightarrow \left\{ \begin{array}{l}8 - x \ge 0\\4\left( {3x - 8} \right) = 64 - 16x + {x^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \le 8\\{x^2} - 28x + 96 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 8\\\left[ \begin{array}{l}x = 4\\x = 24\end{array} \right.\end{array} \right. \Leftrightarrow x = 4\;\;\left( {tm} \right)\end{array}\) Vậy phương trình có tập nghiệm: \(S = \left\{ 4 \right\}.\) Chọn A. Câu hỏi 50 : Cho hai hàm số \(y = \left( {m + 1} \right){x^2} + 3{m^2}x + m\) và \(y = \left( {m + 1} \right){x^2} + 12x + 2\). Tìm tất cả các giá trị của m để đồ thị hai hàm số đã cho không cắt nhau.
Đáp án: B Phương pháp giải: +) Để hai đồ thị hàm số không cắt nhau thì phương trình hoành độ giao điểm của 2 đồ thị hàm số vô nghiệm. +) Phương trình dạng \(ax + b = 0\) vô nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b \ne 0\end{array} \right.\). Lời giải chi tiết: Xét phương trình hoành độ giao điểm: \(\begin{array}{l}\,\,\,\,\,\,\left( {m + 1} \right){x^2} + 3{m^2}x + m = \left( {m + 1} \right){x^2} + 12x + 2\\ \Leftrightarrow 3{m^2}x + m = 12x + 2 \Leftrightarrow \left( {3{m^2} - 12} \right)x = 2 - m\,\,\left( * \right)\end{array}\) Để hai đồ thị hàm số đã cho không cắt nhau thì phương trình (*) vô nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}3{m^2} - 12 = 0\\2 - m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \pm 2\\m \ne 2\end{array} \right. \Leftrightarrow m = - 2\). Chọn B. Câu hỏi 51 : Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn \(\left[ { - 5;10} \right]\) để phương trình \(\left( {m + 1} \right)x = \left( {3{m^2} - 1} \right)x + m - 1\) có nghiệm duy nhất. Tổng các phần tử trong S bằng:
Đáp án: C Phương pháp giải: Phương trình dạng \(ax + b = 0\) có nghiệm duy nhất \( \Leftrightarrow a \ne 0\). Khi đó phương trình có nghiệm \(x = \dfrac{{ - b}}{a}\). Lời giải chi tiết: Ta có \(\left( {m + 1} \right)x = \left( {3{m^2} - 1} \right)x + m - 1 \Leftrightarrow \left( {3{m^2} - m - 2} \right)x = 1 - m\,\,\left( * \right)\) Phương trình ban đầu có nghiệm duy nhất \( \Leftrightarrow \) phương trình (*) có nghiệm duy nhất \( \Leftrightarrow 3{m^2} - m - 2 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\m \ne \dfrac{{ - 2}}{3}\end{array} \right.\). Kết hợp điều kiện đề bài ta có \(\left\{ \begin{array}{l}m \in Z\\m \in \left[ { - 5;10} \right]\backslash \left\{ 1 \right\}\end{array} \right. \Rightarrow S = \left\{ {m \in Z|m \in \left[ { - 5;10} \right]\backslash \left\{ 1 \right\}} \right\}\). Vậy tổng các phần tử của S bằng \(\left( { - 5} \right) + \left( { - 4} \right) + ... + \left( { - 1} \right) + 0 + 2 + 3 + 4 + ... + 10 = 39\). Chọn C. Câu hỏi 52 : Tìm tất cả các giá trị thực của tham số m để phương trình \(\left( {{m^2} + m} \right)x = m + 1\) có nghiệm duy nhất \(x = 1\).
Đáp án: D Phương pháp giải: Cách 1: Phương trình dạng \(ax + b = 0\) có nghiệm duy nhất \( \Leftrightarrow a \ne 0\). Khi đó phương trình có nghiệm \(x = \dfrac{{ - b}}{a}\). Cách 2: Thay \(x = 1\) vào phương trình tìm m. Với giá trị m vừa tìm được, thử lại xem với giá trị đó phương trình có nghiệm duy nhất \(x = 1\) không và kết luận. Lời giải chi tiết: Cách 1: Để phương trình có nghiệm duy nhất \( \Leftrightarrow {m^2} + m \ne 0 \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 1\end{array} \right.\). Khi đó phương trình có nghiệm duy nhất \(x = \dfrac{{m + 1}}{{{m^2} + m}} = \dfrac{{m + 1}}{{m\left( {m + 1} \right)}} = \dfrac{1}{m}\). Do phương trình có nghiệm duy nhất \(x = 1 \Rightarrow \dfrac{1}{m} = 1 \Leftrightarrow m = 1\,\,\left( {tm} \right)\), Vậy \(m = 1\). Cách 2: Do \(x = 1\) là nghiệm của phương trình đã cho nên thay \(x = 1\) vào phương trình ta có: \({m^2} + m = m + 1 \Leftrightarrow {m^2} = 1 \Leftrightarrow m = \pm 1\). Thử lại: +) Với \(m = 1\), phương trình trở thành \(2x = 2 \Leftrightarrow x = 1 \Rightarrow \) Phương trình có nghiệm duy nhất \(x = 1\). Vậy \(m = 1\) thỏa mãn. +) Với \(m = - 1\), phương trình trở thành \(0x = 0 \Rightarrow \) Phương trình có vô số nghiệm \( \Rightarrow m = - 1\) không thỏa mãn. Vậy \(m = 1\). Chọn D. Câu hỏi 53 : Cho hai hàm số \(y = \left( {m + 1} \right)x + 1\) và \(y = \left( {3{m^2} - 1} \right)x + m\). Tìm tất cả các giá trị thực của tham số m để đồ thị hai hàm số đã cho trùng nhau.
Đáp án: C Phương pháp giải: +) Để hai đồ thị hàm số trùng nhau thì phương trình hoành độ giao điểm của 2 đồ thị hàm số có vô số nghiệm. +) Phương trình dạng \(ax + b = 0\) có vô số nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 0\end{array} \right.\). Lời giải chi tiết: Xét phương trình hoành độ giao điểm \(\left( {m + 1} \right)x + 1 = \left( {3{m^2} - 1} \right)x + m \Leftrightarrow \left( {3{m^2} - m - 2} \right)x = 1 - m\) (*) Để hai đồ thị hàm số trùng nhau thì phương trình (*) có vô số nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}3{m^2} - m - 2 = 0\\1 - m = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 1\\m = \dfrac{{ - 2}}{3}\end{array} \right.\\m = 1\end{array} \right. \Leftrightarrow m = 1\). Chọn C. Câu hỏi 54 : Cho phương trình \(\left( {{m^2} - 2m} \right)x = {m^2} - 3m + 2\). Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm?
Đáp án: D Phương pháp giải: Phương trình dạng \(ax + b = 0\) có nghiệm khi và chỉ khi xảy ra 2 trường hợp: +) Phương trình có nghiệm duy nhất \( \Leftrightarrow a \ne 0\). +) Phương trình có vô số nghiệm \( \Leftrightarrow a = b = 0\). Lời giải chi tiết: TH1 : Phương trình đã cho có nghiệm duy nhất \( \Leftrightarrow {m^2} - 2m \ne 0 \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne 2\end{array} \right.\). TH2 : Phương trình đã cho có vô số nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 2m = 0\\{m^2} - 3m + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.\\\left[ \begin{array}{l}m = 1\\m = 2\end{array} \right.\end{array} \right. \Leftrightarrow m = 2\). Kết hợp 2 trường hợp ta có phương trình có nghiệm \( \Leftrightarrow m \ne 0\). Vậy có vô số giá trị của m thỏa mãn \( \Rightarrow m \ne 0\). Chọn D. Câu hỏi 55 : Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x + {m^2} + 4m + 5 = 0\). Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm đúng với mọi \(x \in R\)?
Đáp án: D Phương pháp giải: Phương trình dạng \(ax + b = 0\) có vô số nghiệm (nghiệm đúng với mọi \(x \in R\))\( \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 0\end{array} \right.\). Lời giải chi tiết: Phương trình đã cho có nghiệm đúng với mọi \(x \in R \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 3m + 2 = 0\\{m^2} + 4m + 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left\{ \begin{array}{l}m = 2\\m = 1\end{array} \right.\\Vo\,\,nghiem\end{array} \right. \Rightarrow \)Không tồn tại m thỏa mãn yêu cầu bài toán. Chọn D. Câu hỏi 56 : Tìm tất cả các giá trị thực của tham số m để phương trình \(\left( {x - 1} \right)\left( {{x^2} - 4mx - 4} \right) = 0\) có ba nghiệm phân biệt.
Đáp án: D Phương pháp giải: +) \(\left( {x - 1} \right)\left( {{x^2} - 4mx - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\,\,\,\left( 1 \right)\\{x^2} - 4mx - 4 = 0\,\,\left( 2 \right)\end{array} \right.\) +) Phương trình đã cho có 3 nghiệm phân biệt khi và chỉ khi phương trình (2) có 2 nghiệm phân biệt không trùng với phương trình (1). Lời giải chi tiết: Ta có : \(\left( {x - 1} \right)\left( {{x^2} - 4mx - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\{x^2} - 4mx - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\g\left( x \right) = {x^2} - 4mx - 4 = 0\end{array} \right.\) Để phương trình ban đầu có 3 nghiệm phân biệt thì : \(\left\{ \begin{array}{l}{\Delta _g}' = {\left( {2m} \right)^2} + 4 > 0\\g\left( 1 \right) \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{m^2} + 4 > 0\,\,\left( {luon\,\,dung} \right)\\1 - 4m - 4 \ne 0\end{array} \right. \Leftrightarrow m \ne - \dfrac{3}{4}\). Chọn D. Câu hỏi 57 : Tìm tất cả các giá trị thực của tham số m để phương trình \(3{x^2} - \left( {m + 2} \right)x + m - 1 = 0\) có một nghiệm gấp đôi nghiệm còn lại.
Đáp án: A Phương pháp giải: +) Tìm điều kiện để phương trình có nghiệm. +) Khi phương trình bậc hai \(a{x^2} + bx + c = 0\) có 2 nghiệm \({x_1},\,\,{x_2}\). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\). Lời giải chi tiết: Xét phương trình \(3{x^2} - \left( {m + 2} \right)x + m - 1 = 0\) ta có: \(\Delta = {\left( {m + 2} \right)^2} - 12\left( {m - 1} \right) = {m^2} - 8m + 16 = {\left( {m - 4} \right)^2} \ge 0\,\,\forall m \Rightarrow \) Phương trình luôn có nghiệm với mọi giá trị của m. Gọi \({x_1},\,\,{x_2}\) là 2 nghiệm của phương trình đã cho, áp dụng định lí Vi-ét ta có : \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{m + 2}}{3}\\{x_1}{x_2} = \dfrac{{m - 1}}{3}\end{array} \right.\,\,\left( * \right)\). Theo bài ra, không mất tính tổng quát ta có : \({x_1} = 2{x_2}\), thay vào (*) ta có : \(\begin{array}{l}\left\{ \begin{array}{l}2{x_2} + {x_2} = \dfrac{{m + 2}}{3}\\2x_2^2 = \dfrac{{m - 1}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = \dfrac{{m + 2}}{9}\\x_2^2 = \dfrac{{m - 1}}{6}\end{array} \right. \Leftrightarrow {\left( {\dfrac{{m + 2}}{9}} \right)^2} = \dfrac{{m - 1}}{6}\\ \Leftrightarrow \dfrac{{{{\left( {m + 2} \right)}^2}}}{{27}} = \dfrac{{m - 1}}{2} \Leftrightarrow 2{m^2} + 8m + 8 = 27m - 27 \Leftrightarrow 2{m^2} - 19m + 35 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 7\\m = \dfrac{5}{2}\end{array} \right.\end{array}\) Chọn A. Câu hỏi 58 : Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 2 = 0\) (m là tham số). Tìm m để biểu thức \(P = {x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) - 6\) đạt giá trị nhỏ nhất.
Đáp án: C Phương pháp giải: +) Khi phương trình bậc hai \(a{x^2} + bx + c = 0\) có 2 nghiệm \({x_1},\,\,{x_2}\). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\). +) Đưa biểu thức \(P\) về dạng \(P = {f^2}\left( m \right) + A\) (\(A\) là hằng số) và đánh giá. Lời giải chi tiết: Phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 2 = 0\) có 2 nghiệm phân biệt \( \Leftrightarrow \Delta ' = {\left( {m + 1} \right)^2} - {m^2} - 2 = 2m - 1 > 0 \Leftrightarrow m > \dfrac{1}{2}\). Giả sử phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 2 = 0\) có hai nghiệm là \({x_1},\,\,{x_2}\). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 2\\{x_1}{x_2} = {m^2} + 2\end{array} \right.\). Khi đó \(\begin{array}{l}P = {x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) - 6 = {m^2} + 2 - 2\left( {2m + 2} \right) - 6\\P = {m^2} - 4m - 8 = {m^2} - 4m + 4 - 12 = {\left( {m - 2} \right)^2} - 12 \ge - 12\end{array}\) \( \Rightarrow {P_{\min }} = - 12\). Dấu "=" xảy ra \( \Leftrightarrow m = 2\). Chọn C. Câu hỏi 59 : Với giá trị nào của \(m\) thì phương trình \(m{x^2} - 2\left( {m - 2} \right)x + 3 - m = 0\) có hai nghiệm trái dấu?
Đáp án: C Phương pháp giải: Phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm trái dấu \( \Leftrightarrow ac < 0.\) Lời giải chi tiết: Phương trình \(m{x^2} - 2\left( {m - 2} \right)x + 3 - m = 0\) có hai nghiệm trái dấu \( \Leftrightarrow m\left( {3 - m} \right) < 0 \Leftrightarrow m\left( {m - 3} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}m > 3\\m < 0\end{array} \right..\) Chọn C. Câu hỏi 60 : Cho \(f\left( x \right) = m\left( {m + 2} \right){x^2} - 2mx + 2\). Tìm m để \(f\left( x \right) = 0\) có hai nghiệm dương phân biệt.
Đáp án: B Phương pháp giải: Phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta > 0\\S > 0\\P > 0\end{array} \right..\) Lời giải chi tiết: Phương trình \(m\left( {m + 2} \right){x^2} - 2mx + 2 = 0\) có hai nghiệm dương phân biệt \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m\left( {m + 2} \right) \ne 0\\\Delta ' = {m^2} - 2m\left( {m + 2} \right) > 0\\S = \frac{{2m}}{{m\left( {m + 2} \right)}} > 0\\P = \frac{2}{{m\left( {m + 2} \right)}} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 2\\ - {m^2} - 4m > 0\\\frac{{2m}}{{m\left( {m + 2} \right)}} > 0\\m\left( {m + 2} \right) > 0\;\;\left( {do\;2 > 0} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 2\\m\left( {m + 4} \right) < 0\\m > 0\\m + 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 2\\ - 4 < m < 0\\m > - 2\\m > 0\end{array} \right. \Rightarrow m \in \emptyset .\end{array}\) Vậy \(m \in \emptyset .\) Chọn B.
|