40 bài tập trắc nghiệm phương trình mức độ vận dụng, vận dụng caoLàm bàiCâu hỏi 1 : Tìm giá trị thực của tham số m để cặp phương trình sau tương đương: \(2{x^2} + mx - 2 = 0\,\,\,\left( 1 \right)\) và \(2{x^3} + \left( {m + 4} \right){x^2} + 2\left( {m - 1} \right)x - 4 = 0\,\,\left( 2 \right)\)
Đáp án: B Phương pháp giải: +) Đưa phương trình (2) về dạng tích, tìm nghiệm \(x = {x_0}\) cụ thể của phương trình (2). +) Do (1) và (2) tương đương nên \(x = {x_0}\) cũng là nghiệm của pt(1). +) Thay nghiệm \(x = {x_0}\) vào pt(1), tìm m. +) Với m tìm được, thử lại xem 2 phương trình có thực sự tương đương và kết luận. Lời giải chi tiết: \(\begin{array}{l}2{x^3} + \left( {m + 4} \right){x^2} + 2\left( {m - 1} \right)x - 4 = 0\,\,\left( 2 \right)\\ \Leftrightarrow 2{x^3} + 4{x^2} + m{x^2} + 2mx - 2x - 4 = 0\\ \Leftrightarrow 2{x^2}\left( {x + 2} \right) + mx\left( {x + 2} \right) - 2\left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {2{x^2} + mx - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\2{x^2} + mx - 2 = 0\end{array} \right.\end{array}\) Do hai phương trình (1) và (2) là tương đương nên \(x = - 2\) cũng là nghiệm của phương tình (1). Thay \(x = - 2\) vào phương trình (1) ta có \(2{\left( { - 2} \right)^2} + m\left( { - 2} \right) - 2 = 0 \Leftrightarrow 2m = 6 \Leftrightarrow m = 3\). Thử lại với \(m = 3\) ta có (1) trở thành \(2{x^2} + 3x - 2 = 0 \Leftrightarrow \left( {x + 2} \right)\left( {2x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = \dfrac{1}{2}\end{array} \right. \Rightarrow {S_1} = \left\{ { - 2;\dfrac{1}{2}} \right\}\). (2) trở thành \(2{x^3} + 7{x^2} + 4x - 4 = 0 \Leftrightarrow {\left( {x + 2} \right)^2}\left( {2x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = \dfrac{1}{2}\end{array} \right. \Leftrightarrow {S_2} = \left\{ { - 2;\dfrac{1}{2}} \right\}\). Vậy \({S_1} = {S_2}\) hay hai phương trình (1) và (2) tương đương khi \(m = 3\). Chọn B. Câu hỏi 2 : Phương trình \(\sqrt {{x^3} - 4{x^2} + 5x - 2} + x = \sqrt {2 - x} \) có bao nhiêu nghiệm ?
Đáp án: B Phương pháp giải: \(\sqrt A \) xác định (có nghĩa) \( \Leftrightarrow A \ge 0\). Lời giải chi tiết: \(\begin{array}{l}\left\{ \begin{array}{l}{x^3} - 4{x^2} + 5x - 2 \ge 0\\2 - x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^3} - 4{x^2} + 4x + x - 2 \ge 0\\x \le 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x\left( {{x^2} - 4x + 4} \right) + \left( {x - 2} \right) \ge 0\\x \le 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x{\left( {x - 2} \right)^2} + \left( {x - 2} \right) \ge 0\\x \le 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 2} \right)\left( {{x^2} - 2x + 1} \right) \ge 0\\x \le 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 2} \right){\left( {x - 1} \right)^2} \ge 0\\x \le 2\end{array} \right.\end{array}\) Do \(\left\{ \begin{array}{l}{\left( {x - 1} \right)^2} \ge 0\\x \le 2 \Leftrightarrow x - 2 \le 0\end{array} \right. \Rightarrow \left( {x - 2} \right){\left( {x - 1} \right)^2} \le 0\) Mà \(\left( {x - 2} \right){\left( {x - 1} \right)^2} \ge 0 \Leftrightarrow \) dấu "=" xảy ra \( \Leftrightarrow \left( {x - 2} \right){\left( {x - 1} \right)^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\). Thử lại với \(x = 1\) ta có \(\sqrt 0 + 1 = \sqrt 1 \) (đúng) Với \(x = 2\) ta có \(\sqrt 0 + 2 = \sqrt 0 \) (vô lí) Vậy phương trình đã cho có 1 nghiệm \(x = 1\). Chọn B. Câu hỏi 3 :
Phương pháp giải: Lời giải chi tiết: Điều kiện: \(\left| {x - 4} \right| - 1 \ne 0 \Leftrightarrow \left| {x - 4} \right| \ne 1 \Leftrightarrow \left\{ \begin{array}{l}x - 4 \ne 1\\x - 4 \ne - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 5\\x \ne 3\end{array} \right.\) Lập bảng xét dấu hai biểu thức x+3 và x-4: Trường hợp 1: Với \(x \le - 3\) thì: Phương trình \( \Leftrightarrow \frac{3}{{ - x + 4 - 1}} = - x - 3 \Leftrightarrow \frac{3}{{3 - x}} = - x - 3 \Leftrightarrow {x^2} = 12 \Leftrightarrow \left[ \begin{array}{l}x = 2\sqrt 3 {\rm{ }} \, \,(ktm)\\x = - 2\sqrt 3 \end{array} \right.\) Trường hợp 2: Với \( - 3 < x < 4\) thì: Phương trình \( \Leftrightarrow \frac{3}{{ - x + 4 - 1}} = x + 3 \Leftrightarrow \frac{3}{{3 - x}} = x + 3 \Leftrightarrow {x^2} = 6 \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 6 {\rm{ }}\\x = - \sqrt 6 \end{array} \right.\) Trường hợp 3: Với \(x \ge 4\) thì: Phương trình \( \Leftrightarrow \frac{3}{{x - 4 - 1}} = x + 3 \Leftrightarrow \frac{3}{{x - 5}} = x + 3 \Leftrightarrow {x^2} - 2x - 18 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 - \sqrt {19} {\rm{ \, \, (ktm) }}\\x = 1 + \sqrt {19} \end{array} \right.\) Vậy phương trình có 4 nghiệm là: \(x = - 2\sqrt 3 ;x = \pm \sqrt 6 ;x = 1 + \sqrt 19 \) Câu hỏi 4 : Tập nghiệm của phương trình\(\sqrt{x+5-4\sqrt{x+1}}+\sqrt{x+2-2\sqrt{x+1}}=1\) là:
Đáp án: B Phương pháp giải: Phương pháp: + Phương trình có dạng: \(\sqrt{f(x)}+\sqrt{g(x)}=c\) trong đó \(f(x)={{h}^{2}}(x);\,\,\,g(x)={{k}^{2}}(x)\) + Khi đó phương trình được đưa về dạng \(\sqrt{{{h}^{2}}(x)}+\sqrt{{{k}^{2}}(x)}=c\Leftrightarrow \left| h(x) \right|+\left| k(x) \right|=c\). Bỏ dấu trị tuyệt đối theo định nghĩa \(A=\left\{ \begin{align} & \,\,\begin{matrix} A & khi & A\ge 0 \\\end{matrix} \\ & \begin{matrix} -A & khi & A<0 \\\end{matrix} \\\end{align} \right.\). Giải phương trình ta tìm được x Lời giải chi tiết: Điều kiện: \(x+1\ge 0\Leftrightarrow x\ge -1\) Ta có: \(\begin{align} & x+5-4\sqrt{x+1}=x+1-4\sqrt{x+1}+4={{\left( \sqrt{x+1}-2 \right)}^{2}} \\ & x+2-2\sqrt{x+1}=x+1-2\sqrt{x+1}+1={{\left( \sqrt{x+1}-1 \right)}^{2}} \\\end{align}\) Phương trình: \(\begin{align} & \sqrt{x+5-4\sqrt{x+1}}+\sqrt{x+2-2\sqrt{x+1}}=1\Leftrightarrow \sqrt{{{\left( \sqrt{x+1}-2 \right)}^{2}}}+\sqrt{{{\left( \sqrt{x+1}-1 \right)}^{2}}}=1 \\ & \Leftrightarrow \left| \sqrt{x+1}-2 \right|+\left| \sqrt{x+1}-1 \right|=1\,\,\,\,\,\left( 1 \right) \\\end{align}\) +) Trường hợp 1: Nếu \(\sqrt{x+1}\ge 2\Leftrightarrow x+1\ge 4\Leftrightarrow x\ge 3\) thì: \(\left\{ \begin{align} & \left| \sqrt{x+1}-2 \right|=\sqrt{x+1}-2 \\ & \left| \sqrt{x+1}-1 \right|=\sqrt{x+1}-1 \\\end{align} \right.\) \(\left( 1 \right)\,\,\Leftrightarrow \sqrt{x+1}-2+\sqrt{x+1}-1=1\Leftrightarrow \sqrt{x+1}=2\Leftrightarrow x+1=4\Leftrightarrow x=3\,\,\,\left( tm \right)\) +) Trường hợp 2: Nếu \(\sqrt{x+1}\le 1\Leftrightarrow x+1\le 1\Leftrightarrow x\le 0\) thì: \(\left\{ \begin{align} & \left| \sqrt{x+1}-2 \right|=2-\sqrt{x+1} \\ & \left| \sqrt{x+1}-1 \right|=1-\sqrt{x+1} \\\end{align} \right.\) \(\left( 1 \right)\Leftrightarrow 2-\sqrt{x+1}+1-\sqrt{x+1}=1\Leftrightarrow \sqrt{x+1}=1\Leftrightarrow x+1=1\Leftrightarrow x=0\,\,\,\left( tm \right)\) +) Trường hợp 3: Nếu \(1<\sqrt{x+1}<2\Leftrightarrow 1<x+1<4\Leftrightarrow 0<x<3\) thì: \(\left\{ \begin{align} & \left| \sqrt{x+1}-2 \right|=2-\sqrt{x+1} \\ & \left| \sqrt{x+1}-1 \right|=\sqrt{x+1}-1 \\\end{align} \right.\) \((1)\Leftrightarrow 2-\sqrt{x+1}+\sqrt{x+1}-1=1\) \(\Leftrightarrow 1=1\) (luôn đúng với \(\forall x \in \)(0; 3) ) Vậy tập nghiệm của phương trình là [0; 3] Chọn B. Câu hỏi 5 : Số nghiệm của phương trình \(\sqrt[3]{{x + 1}} + \sqrt[3]{{2{x^2} + 1}} = \sqrt[3]{{x + 2}} + \sqrt[3]{{2{x^2}}}\) là:
Đáp án: A Phương pháp giải: \(\begin{array}{l}+ \,\,\,\sqrt[3]{{f(x)}} + \sqrt[3]{{g(x)}} = \sqrt[3]{{h(x)}} + \sqrt[3]{{k(x)}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\\Leftrightarrow {\left( {\sqrt[3]{{f(x)}} + \sqrt[3]{{g(x)}}} \right)^3} = {\left( {\sqrt[3]{{h(x)}} + \sqrt[3]{{k(x)}}} \right)^3}\\\Leftrightarrow f(x) + g(x) + 3\sqrt[3]{{f(x).g(x)}}\left( {\sqrt[3]{{f(x)}} + \sqrt[3]{{g(x)}}} \right) = h(x) + k(x) + 3\sqrt[3]{{h(x).k(x)}}\left( {\sqrt[3]{{h(x)}} + \sqrt[3]{{k(x)}}} \right)\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array}\) + Thay (1) vào (2) ta giải phương trình ta tìm được x. Lời giải chi tiết: Ta có: \[\begin{array}{l}\sqrt[3]{{x + 1}} + \sqrt[3]{{2{x^2} + 1}} = \sqrt[3]{{x + 2}} + \sqrt[3]{{2{x^2}}} \Leftrightarrow {\left( {\sqrt[3]{{x + 1}} + \sqrt[3]{{2{x^2} + 1}}} \right)^3} = {\left( {\sqrt[3]{{x + 2}} + \sqrt[3]{{2{x^2}}}} \right)^3}\\ \Leftrightarrow x + 1 + 2{{\rm{x}}^2} + 1 + 3\sqrt[3]{{\left( {x + 1} \right)\left( {2{{\rm{x}}^2} + 1} \right)}}\left( {\sqrt[3]{{x + 1}} + \sqrt[3]{{2{{\rm{x}}^2} + 1}}} \right) = x + 2 + 2{{\rm{x}}^2} + 3\sqrt[3]{{\left( {x + 2} \right)2{{\rm{x}}^2}}}\left( {\sqrt[3]{{x + 2}} + \sqrt[3]{{2{{\rm{x}}^2}}}} \right)\\ \Leftrightarrow 3\sqrt[3]{{\left( {x + 1} \right)\left( {2{{\rm{x}}^2} + 1} \right)}}\left( {\sqrt[3]{{x + 1}} + \sqrt[3]{{2{{\rm{x}}^2} + 1}}} \right) = 3\sqrt[3]{{\left( {x + 2} \right)2{{\rm{x}}^2}}}\left( {\sqrt[3]{{x + 2}} + \sqrt[3]{{2{{\rm{x}}^2}}}} \right)\\ \Leftrightarrow \sqrt[3]{{\left( {x + 1} \right)\left( {2{{\rm{x}}^2} + 1} \right)}}\left( {\sqrt[3]{{x + 2}} + \sqrt[3]{{2{{\rm{x}}^2}}}} \right) = \sqrt[3]{{\left( {x + 2} \right)2{{\rm{x}}^2}}}\left( {\sqrt[3]{{x + 2}} + \sqrt[3]{{2{{\rm{x}}^2}}}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\left( {\sqrt[3]{{x + 2}} + \sqrt[3]{{2{{\rm{x}}^2}}}} \right) = 0\\\left( {\sqrt[3]{{\left( {x + 2} \right)2{{\rm{x}}^2}}} - \sqrt[3]{{\left( {x + 1} \right)\left( {2{{\rm{x}}^2} + 1} \right)}}} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sqrt[3]{{x + 2}} = - \sqrt[3]{{2{{\rm{x}}^2}}}\\\sqrt[3]{{\left( {x + 2} \right)2{{\rm{x}}^2}}} = \sqrt[3]{{\left( {x + 1} \right)\left( {2{{\rm{x}}^2} + 1} \right)}}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = - 2{{\rm{x}}^2}\\2{{\rm{x}}^3} + 4{{\rm{x}}^2} = 2{{\rm{x}}^3} + 2{{\rm{x}}^2} + x + 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2{{\rm{x}}^2} + x + 2 = 0\\2{{\rm{x}}^2} - x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - \frac{1}{2}\end{array} \right.\end{array}\] (Vì phương trình:\(2{{\text{x}}^{2}}+x+2=0\) có \(\Delta\) < 0 nên vô nghiệm) Vậy phương trình có hai nghiệm phân biệt Chọn A. Câu hỏi 6 : Số nghiệm của phương trình\(\sqrt {2{\rm{x}} - 1} + {x^2} - 3{\rm{x + 1 = 0}}\) là:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Điều kiện: \(2{\rm{x}} - 1 \ge 0 \Leftrightarrow x \ge \dfrac{1}{2}\) Đặt \(t = \sqrt {2{\rm{x}} - 1} \left( {t \ge 0} \right) \Rightarrow x = \dfrac{{{t^2} + 1}}{2}(*)\).Thay (*) vào phương trình, ta được: \(t + {\left( {\dfrac{{{t^2} + 1}}{2}} \right)^2} - 3\left( {\dfrac{{{t^2} + 1}}{2}} \right) + 1 = 0 \Leftrightarrow {t^4} - 4{t^2} + 4t - 1 = 0 \Leftrightarrow {\left( {t - 1} \right)^2}\left( {{t^2} + 2t - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {tm} \right)\\t = \sqrt 2 - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {tm} \right)\\t = - \sqrt 2 - 1\,\,\,\,\,\,\,\,\,\left( {ktm} \right)\end{array} \right.\) +) Với t = 1 \( \Leftrightarrow 1 = \sqrt {2{\rm{x}} - 1} \Leftrightarrow x = 1\) +) Với \(t = \sqrt 2 - 1 \Leftrightarrow \sqrt 2 - 1 = \sqrt {2{\rm{x}} - 1} \Leftrightarrow x = 2 - \sqrt 2 \) Vậy phương trình có 2 nghiệm. Chọn A. Câu hỏi 7 : Tổng bình phương các nghiệm của phương trình \(\sqrt {4{{\rm{x}}^2} + x + 6} = 4{\rm{x}} - 2 + 7\sqrt {x + 1} \) là:
Đáp án: C Phương pháp giải: + Phân tích từng vế của phương trình để xuất hiện nhân tử chung + Chia cả 2 vế của phương trình cho \(\sqrt {x + 1} \)với điều kiện x > 1 + Đặt \(t = \dfrac{{2{\rm{x}} - 1}}{{\sqrt {x + 1} }}\) suy ra phương trình ẩn t Lời giải chi tiết: Điều kiện : \(x + 1 \ge 0 \Leftrightarrow x \ge - 1\) Ta có: \(\sqrt {4{{\rm{x}}^2} + x + 6} = 4{\rm{x}} - 2 + 7\sqrt {x + 1} \Leftrightarrow \sqrt {4{{\rm{x}}^2} - 4x + 1 + 5{\rm{x}} + 5} = 2(2{\rm{x}} - 1) + 7\sqrt {x + 1} \) \(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {2{\rm{x}} - 1} \right)}^2} + 5\left( {{\rm{x}} + 1} \right)} = 2\left( {2{\rm{x}} - 1} \right) + 7\sqrt {x + 1} \\ \Leftrightarrow \sqrt {{{\dfrac{{\left( {2{\rm{x}} - 1} \right)}}{{x + 1}}}^2} + 5} = 2.\dfrac{{2{\rm{x}} - 1}}{{\sqrt {x + 1} }} + 7\end{array}\) Đặt \(t = \dfrac{{2{\rm{x}} - 1}}{{\sqrt {x + 1} }}\), phương trình trở thành:\(\sqrt {{t^2} + 5} = 2t + 7\) Điều kiện \(2t + 7 \ge 0 \Leftrightarrow t \ge - \dfrac{7}{2}\) Phương trình: \(\begin{array}{l} \Leftrightarrow {t^2} + 5 = {\left( {2t + 7} \right)^2} \Leftrightarrow {t^2} + 5 = 4{t^2} + 28t + 49\\ \Leftrightarrow 3{t^2} + 28t + 44 = 0 \Leftrightarrow \left[ \begin{array}{l}t = - 2\,\,\,\,\,\,\,\,\,\left( {tm} \right)\\t = - \dfrac{{22}}{3}\,\,\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) +) Với \(t = - 2 \Leftrightarrow - 2 = \dfrac{{2{\rm{x}} - 1}}{{\sqrt {x + 1} }} \Leftrightarrow \sqrt {x + 1} = - x + \dfrac{1}{2}\,\,\,\left( * \right)\) Điều kiện \( - x + \dfrac{1}{2} \ge 0 \Leftrightarrow x \le \dfrac{1}{2}\) Khi đó \(\left( * \right) \Leftrightarrow x + 1 = {x^2} - x + \dfrac{1}{4} \Leftrightarrow {x^2} - 2x - \dfrac{3}{4} \Leftrightarrow 4{x^2} - 8x - 3 = 0\,\,\,\,\,\,\left( 1 \right)\) Giả sử x1, x2 là hai nghiệm của phương trình (1) Theo Vi – et, ta có : \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}.{x_2} = - \dfrac{3}{4}\end{array} \right. \Rightarrow {x_1}^2 + {x_2}^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}.{x_2} = 4 + \dfrac{3}{2} = \dfrac{{11}}{2}\) Chọn C. Câu hỏi 8 : Có bao nhiêu giá trị nguyên của tham số m trên đoạn \(\left[ { - 6;60} \right]\) để phương trình \(\sqrt {{x^2} - 2x + 2} + 2{x^2} = 2m + 1 + 4x\) có nghiệm?
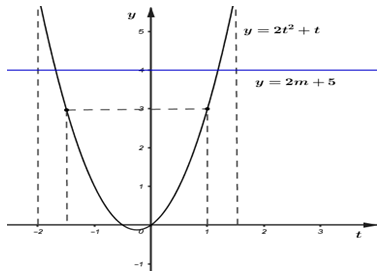
Đáp án: D Phương pháp giải: Đặt \(\sqrt {{x^2} - 2x + 2} = t\,\,(t \ge 0)\). Tìm điều kiện của t, biện luận nghiệm của phương trình. Lời giải chi tiết: Tập xác định \(D = R\) \(\sqrt {{x^2} - 2x + 2} + 2{x^2} = 2m + 1 + 4x\,\,\,\,\,(1)\,\, \Leftrightarrow 2{x^2} - 4x + 4 + \sqrt {{x^2} - 2x + 2} - 2m - 5 = 0\) Đặt \(\sqrt {{x^2} - 2x + 2} = t\,\,\) Vì \({x^2} - 2x + 2 = {\left( {x - 1} \right)^2} + 1 \ge 1\) với mọi x nên \(t \ge 1\) Phương trình thành \(2{t^2} + t - 2m - 5 = 0\;\;\left( 2 \right) \Leftrightarrow 2{t^2} + t = 2m + 5\) Số nghiệm của phương trình \(\left( 2 \right)\) là số giao điểm của đường thẳng \(y = 2m + 5\) với đồ thị hàm số \(y = 2{t^2} + t\) Ta có đồ thị hàm số \(y = 2{t^2} + t\) như hình vẽ: Phương trình (2) có nghiệm \(t \ge 1 \Leftrightarrow \) đường thẳng \(y = 2m + 5\) cắt đồ thị hàm số \(y = 2{t^2} + t\) tại ít nhất một điểm có hoành độ \(t \ge 1\) Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 2m + 5\) cắt đồ thị hàm số \(y = 2{t^2} + t\) tại ít nhất một điểm có hoành độ \(t \ge 1 \Leftrightarrow 2m + 5 \ge 3 \Leftrightarrow m \ge - 1.\) Mà \(\left\{ \begin{array}{l}m \in Z\\m \in \left[ { - 6;\;60} \right]\end{array} \right. \Rightarrow m \in \left\{ { - 1;\;0;\;1;.......;\;60} \right\}\) Vậy có 62 giá trị thỏa mãn. Chọn D. Câu hỏi 9 : Tìm tất cả các giá trị của tham số \(m\) để phương trình: \({x^2} + 4x + 4\sqrt {21 - {x^2} - 4x} + 2m - 1 = 0\) có bốn nghiệm thực phân biệt.
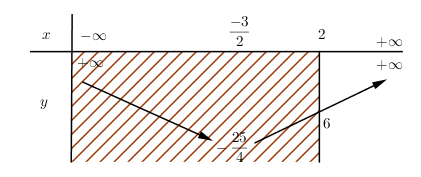
Đáp án: D Phương pháp giải: Đặt \(\sqrt {21 - {x^2} - 4x} = t\,\;\left( {t \ge 0} \right)\). Tìm điều kiện của t, lập bảng biến thiên, biện luận nghiệm của phương trình. Lời giải chi tiết: Điều kiện xác định: \(21 - {x^2} - 4x \ge 0 \Leftrightarrow - 7 \le x \le 3.\) \(\begin{array}{l}\;\;\;\;\;{x^2} + 4x + 4\sqrt {21 - {x^2} - 4x} + 2m - 1 = 0\;\;\;\left( 1 \right)\\ \Leftrightarrow 21 - {x^2} - 4x - 4\sqrt {21 - {x^2} - 4x} = 2m + 20.\end{array}\) Ta có \(21 - {x^2} - 4x = - {x^2} - 4x - 4 + 25 = - {\left( {x + 2} \right)^2} + 25 \le 25\;\forall x \in \left[ { - 7;\;3} \right].\) \( \Rightarrow 0 \le \sqrt {21 - {x^2} - 4x} \le \sqrt {25} = 5.\) Đặt \(\sqrt {21 - {x^2} - 4x} = t\, \Rightarrow t \in \left[ {0;5} \right]\) Khi đó phương trình (1) trở thành: \({t^2} - 4t = 2m + 20\) (2) Khi đó số nghiệm của phương trình \(\left( 2 \right)\) là số giao điểm của đồ thị hàm số \(y = f\left( t \right) = {t^2} - 4t\) và đường thẳng \(y = 2m + 20.\) Xét hàm số \(f\left( t \right) = {t^2} - 4t\) trên đoạn \(\left[ {0;5} \right]\) , ta có bảng biến thiên: Phương trình (1) có 4 nghiệm phân biệt \(x \in \left[ { - 7;\;3} \right] \Leftrightarrow \) Phương trình (2) có 2 nghiệm phân biệt \(t \in \left[ {0;5} \right].\) \( \Leftrightarrow - 4 < 2m + 20 \le 0 \Leftrightarrow - 12 < m \le - 10\) Vậy với \(m \in \left( { - 12;\left. { - 10} \right]} \right.\) thỏa mãn yêu cầu đề bài. Chọn D
Câu hỏi 10 : Giải phương trình :\({x^2} - 2x - 3 = \sqrt {x + 3} \)
Đáp án: A Phương pháp giải: Biến đổi phương trình về dạng \(\left| {f\left( x \right)} \right| = g\left( x \right) > 0\) để giải: Giải phương trình: \(\left| {f\left( x \right)} \right| = g\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = g\left( x \right)\\f\left( x \right) = - g\left( x \right)\end{array} \right.\) Lời giải chi tiết: Giải phương trình :\({x^2} - 2x - 3 = \sqrt {x + 3} \) (1) ĐKXĐ: \(x + 3 \ge 0 \Leftrightarrow x \ge - 3\) \(\begin{array}{l}\left( 1 \right) \Leftrightarrow {x^2} - x + \frac{1}{4} = x + 3 + \sqrt {x + 3} + \frac{1}{4} \Leftrightarrow {\left( {x - \frac{1}{2}} \right)^2} = {\left( {\sqrt {x + 3} + \frac{1}{2}} \right)^2}\\ \Leftrightarrow \left| {x - \frac{1}{2}} \right| = \sqrt {x + 3} + \frac{1}{2}\;\;\;\left( {do\;\;\sqrt {x + 3} + \frac{1}{2} > 0\;\;\forall x \ge - 3} \right).\\TH1:\;x - \frac{1}{2} = \sqrt {x + 3} + \frac{1}{2} \Leftrightarrow x - 1 = \sqrt {x + 3} \\ \Leftrightarrow \left\{ \begin{array}{l}x - 1 \ge 0\\{x^2} - 2x + 1 = x + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} - 3x - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\\left[ \begin{array}{l}x = \frac{{3 + \sqrt {17} }}{2}\\x = \frac{{3 - \sqrt {17} }}{2}\end{array} \right.\end{array} \right. \Leftrightarrow x = \frac{{3 + \sqrt {17} }}{2}\;\;\;\left( {tm} \right)\\TH2:\;x - \frac{1}{2} = - \sqrt {x + 3} - \frac{1}{2} \Leftrightarrow - x = \sqrt {x + 3} \\ \Leftrightarrow \left\{ \begin{array}{l} - x \ge 0\\{x^2} = x + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\{x^2} - x - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\\left[ \begin{array}{l}x = \frac{{1 + \sqrt {13} }}{2}\\x = \frac{{1 - \sqrt {13} }}{2}\end{array} \right.\end{array} \right. \Leftrightarrow x = \frac{{1 - \sqrt {13} }}{2}\;\;\left( {tm} \right)\end{array}\) Vậy \(x = \frac{{3 + \sqrt {17} }}{2}\) hoặc \(x = \frac{{1 - \sqrt {13} }}{2}.\) Chọn A. Câu hỏi 11 : Tìm tất cả các số thực m để phương trình \(\left| {{x^2} - 2x} \right| - m = 0\) có bốn nghiệm phân biệt
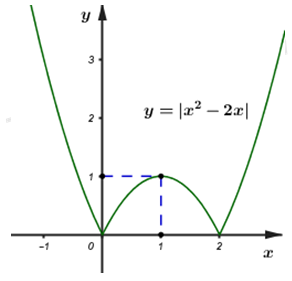
Đáp án: B Phương pháp giải: +) Số nghiệm của phương trình đã cho là số giao điểm của đồ thị hàm số \(y = \left| {{x^2} - 2x} \right|\) và đường thẳng \(y = m.\) +) Khảo sát và vẽ đồ thị hàm số hàm số \(y = \left| {{x^2} - 2x} \right|\) sau đó biện luận số giao điểm của 2 đồ thị hàm số rồi chọn đáp án đúng. Lời giải chi tiết: \(\left| {{x^2} - 2x} \right| - m = 0 \Leftrightarrow \left| {{x^2} - 2x} \right| = m\) (1) Số nghiệm của phương trình (1) là số giao điểm của đồ thị hàm số \(y = \left| {{x^2} - 2x} \right|\) và đường thẳng \(y = m.\) Khảo sát hàm số \(y = \left| {{x^2} - 2x} \right|\): TXĐ: \(D = R\) Vẽ đồ thị của hàm số \(y = \left| {{x^2} - 2x} \right|\) bằng cách giữ nguyên phần phía trên trục Ox và lấy đối xứng phần đồ thị phía dưới trục Ox của hàm số \(y = {x^2} - 2x\). Xét hàm số \(y = {x^2} - 2x\) có đỉnh là \(I\left( {1; - 1} \right)\) Ta có đồ thị hàm số \(y = \left| {{x^2} - 2x} \right|\): Dựa vào đồ thị hàm số ta có đường thẳng \(y = m\) cắt đồ thị hàm số \(y = \left| {{x^2} - 2x} \right|\) tại 4 điểm phân biệt \( \Leftrightarrow 0 < m < 1.\) Chọn B. Câu hỏi 12 : Tìm tất cả các số thực m để phương trình \((m{x^2} + 2x - m + 1)\sqrt x = 0\) có hai nghiệm phân biệt.
Đáp án: A Phương pháp giải: Giải và biện luận phương trình. Lời giải chi tiết: Điều kiện : \(x \ge 0.\) \(\begin{array}{l}\;\;\;\;(m{x^2} + 2x - m + 1)\sqrt x = 0\;\;\left( 1 \right)\\ \Leftrightarrow \left[ \begin{array}{l}m{x^2} + 2x - m + 1 = 0\\\sqrt x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}g\left( x \right) = m{x^2} + 2x - m + 1 = 0\,\,\,\,\,(2)\\x = 0\end{array} \right.\end{array}\) Với \(m = 0\) phương trình \(\left( 1 \right) \Leftrightarrow \left( {2x + 1} \right)\sqrt x = 0 \Leftrightarrow \left[ \begin{array}{l}x = - \frac{1}{2}\;\;\left( {ktm} \right)\\x = 0\end{array} \right.\) \( \Rightarrow m = 0\) không thỏa mãn. Với \(m \ne 0\), xét (2) có \(\Delta ' = 1 - m\left( { - m + 1} \right) = {m^2} - m + 1 = {m^2} - m + \frac{1}{4} + \frac{3}{4} = {\left( {m - \frac{1}{2}} \right)^2} + \frac{3}{4} > 0\) với \(\forall m \ne 0\) \( \Rightarrow \) (2) có 2 nghiệm phân biệt với \(\forall m \ne 0\) Để (1) có 2 nghiệm phân biệt \( \Leftrightarrow \) (2) có 1 nghiệm dương và 1 nghiệm bằng 0 hoặc có 2 nghiệm trái dấu \( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l} - \frac{b}{a} > 0\\\frac{c}{a} = 0\end{array} \right.\\ac < 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l} - m + 1 = 0\\ - \frac{2}{m} > 0\end{array} \right.\\m\left( { - m + 1} \right) < 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m = 1\\m < 0\end{array} \right.\\m > 1\\m < 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > 1\\m < 0\end{array} \right..\) Chọn A. Câu hỏi 13 : Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - 2\left( {m - 1} \right)x + 2{m^2} - 3m + 1 = 0\) (m là tham số). Tìm giá trị lớn nhất \({P_{\max }}\) của biểu thức \(P = \left| {{x_1} + {x_2} + {x_1}{x_2}} \right|\).
Đáp án: C Phương pháp giải: +) Tìm điều kiện để phương trình có 2 nghiệm. +) Khi phương trình bậc hai \(a{x^2} + bx + c = 0\) có 2 nghiệm \({x_1},\,\,{x_2}\). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\). +) Xét dấu biểu thức trong trị tuyệt đối, phá trị tuyệt đối, đưa biểu thức P về dạng \(P = - {f^2}\left( m \right) + A\) (\(A\) là hằng số) và đánh giá. Lời giải chi tiết: Phương trình \({x^2} - 2\left( {m - 1} \right)x + 2{m^2} - 3m + 1 = 0\) có 2 nghiệm \( \Leftrightarrow \Delta ' = {\left( {m - 1} \right)^2} - 2{m^2} + 3m - 1 = - {m^2} + m \ge 0 \Leftrightarrow 0 \le m \le 1\). Giả sử phương trình \({x^2} - 2\left( {m - 1} \right)x + 2{m^2} - 3m + 1 = 0\) có hai nghiệm là \({x_1},\,\,{x_2}\). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m - 2\\{x_1}{x_2} = 2{m^2} - 3m + 1\end{array} \right.\). Khi đó ta có : \(P = \left| {{x_1} + {x_2} + {x_1}{x_2}} \right| = \left| {2m - 2 + 2{m^2} - 3m + 1} \right| = \left| {2{m^2} - m - 1} \right|\). \( \Rightarrow P = 2\left| {{m^2} - \dfrac{1}{2}m - \dfrac{1}{2}} \right| = 2\left| {{m^2} - 2m.\dfrac{1}{4} + \dfrac{1}{{16}} - \dfrac{9}{{16}}} \right| = 2\left| {{{\left( {m - \dfrac{1}{4}} \right)}^2} - \dfrac{9}{{16}}} \right|\) Ta có : \(\begin{array}{l}0 \le m \le 1 \Leftrightarrow \dfrac{{ - 1}}{4} \le m - \dfrac{1}{4} \le \dfrac{3}{4} \Leftrightarrow {\left( {m - \dfrac{1}{4}} \right)^2} \le \dfrac{9}{{16}} \Leftrightarrow {\left( {m - \dfrac{1}{4}} \right)^2} - \dfrac{9}{{16}} \le 0\\ \Rightarrow \left| {{{\left( {m - \dfrac{1}{4}} \right)}^2} - \dfrac{9}{{16}}} \right| = \dfrac{9}{{16}} - {\left( {m - \dfrac{1}{4}} \right)^2} \Rightarrow P = 2\left[ {\dfrac{9}{{16}} - {{\left( {m - \dfrac{1}{4}} \right)}^2}} \right] = \dfrac{9}{8} - 2{\left( {m - \dfrac{1}{4}} \right)^2} \le \dfrac{9}{8}\end{array}\) Vậy \({P_{\max }} = \dfrac{9}{8}\). Chọn C. Câu hỏi 14 : Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - mx + m - 1 = 0\) (m là tham số). Tìm m để biểu thức \(P = \dfrac{{2{x_1}{x_2} + 3}}{{x_1^2 + x_2^2 + 2\left( {{x_1}{x_2} + 1} \right)}}\) đạt giá trị lớn nhất.
Đáp án: B Phương pháp giải: +) Tìm điều kiện để phương trình có 2 nghiệm. +) Khi phương trình bậc hai \(a{x^2} + bx + c = 0\) có 2 nghiệm \({x_1},\,\,{x_2}\). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\). +) Xét \(P - 1\) và đánh giá. Lời giải chi tiết: Xét phương trình \({x^2} - mx + m - 1 = 0\) ta có \(\Delta = {m^2} - 4\left( {m - 1} \right) = {\left( {m - 2} \right)^2} \ge 0\,\,\forall m\) do đó phương trình đã cho luôn có nghiệm với mọi giá trị của m. Giả sử phương trình \({x^2} - mx + m - 1 = 0\) có hai nghiệm là \({x_1},\,\,{x_2}\). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = m - 1\end{array} \right.\). \( \Rightarrow x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {m^2} - 2\left( {m - 1} \right) = {m^2} - 2m + 2\) Khi đó \(P = \dfrac{{2{x_1}{x_2} + 3}}{{x_1^2 + x_2^2 + 2\left( {{x_1}{x_2} + 1} \right)}} = \dfrac{{2m - 2 + 3}}{{{m^2} - 2m + 2 + 2\left( {m - 1 + 1} \right)}} = \dfrac{{2m + 1}}{{{m^2} + 2}}\) Xét \(P - 1 = \dfrac{{2m + 1}}{{{m^2} + 2}} - 1 = \dfrac{{2m + 1 - {m^2} - 2}}{{{m^2} + 2}} = \dfrac{{ - {m^2} + 2m - 1}}{{{m^2} + 2}} = - \dfrac{{{{\left( {m - 1} \right)}^2}}}{{{m^2} + 2}} \le 0\,\,\forall m \in \mathbb{R}\) \( \Rightarrow P \le 1\,\,\forall m \in \mathbb{R}\). Dấu "=" xảy ra \( \Leftrightarrow m - 1 = 0 \Leftrightarrow m = 1\). Chọn B. Câu hỏi 15 : Cho \(a,b,c,d\) là các số thực khác 0. Biết \(c\) và \(d\) là hai nghiệm của phương trình \({x^2} + ax + b = 0\) với \(a,\,\,b\) là hai nghiệm của phương trình \({x^2} + cx + d = 0\). Tính giá trị của biểu thức \(S = a + b + c + d\).
Đáp án: A Phương pháp giải: Lời giải chi tiết: Vì \(c,\,\,d\) là 2 nghiệm của phương trình \({x^2} + ax + b = 0\) nên áp dụng định lí Vi-ét ta có : \(c + d = - a\). Vì \(a,\,\,b\) là 2 nghiệm của phương trình \({x^2} + cx + d = 0\) nên áp dụng định lí Vi-ét ta có : \(a + b = - c\). \( \Rightarrow \) Ta có hệ phương trình \(\left\{ \begin{array}{l}c + d = - a\\a + b = - c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + c = - d\\a + c = - b\end{array} \right. \Leftrightarrow b = d\). Do \(c\) là nghiệm của phương trình \({x^2} + ax + b = 0\) nên \({c^2} + ac + b = 0\) (1) Do \(a\) là nghiệm của phương trình \({x^2} + cx + d = 0\) nên \({a^2} + ca + d = 0\) (2) Trừ vế cho vế của (1) và (2) ta được : \({c^2} - {a^2} + b - d = 0 \Leftrightarrow {c^2} - {a^2} = 0 \Leftrightarrow \left[ \begin{array}{l}a = c\\a = - c\end{array} \right.\) TH1 : \(a = - c \Rightarrow c + d = - a = c \Leftrightarrow d = 0\) (loại) TH2: \(a = c \Rightarrow c + d = - a = - c \Leftrightarrow 2c = - d = - b\) Thay vào (1) ta có : \({c^2} + c = 2c \Leftrightarrow {c^2} - c = 0 \Leftrightarrow \left[ \begin{array}{l}c = 0\,\,\left( {ktm} \right)\\c = 1\,\,\left( {tm} \right)\end{array} \right.\) Khi \(c = 1 \Rightarrow a = c = 1,\,\,b = d = - 2c = - 2 \Rightarrow S = a + b + c + d = 1 - 2 + 1 - 2 = - 2\). Chọn A. Câu hỏi 16 : Giải phương trình \(\left( {x + 8} \right)\sqrt {x + 7} = {x^2} + 10x + 6\).
Đáp án: C Phương pháp giải: Tách ghép vế bên phải để xuất hiện nhân tử chung và dùng phương pháp đánh giá. Lời giải chi tiết: Giải phương trình \(\left( {x + 8} \right)\sqrt {x + 7} = {x^2} + 10x + 6\). Điều kiện: \(x \ge - 7\). \(\begin{array}{l}\,\,\,\,\,\,\,\left( {x + 8} \right)\sqrt {x + 7} = {x^2} + 10x + 6\,\\ \Leftrightarrow \left( {x + 8} \right)\sqrt {x + 7} - {x^2} - 10x - 6 = 0\\ \Leftrightarrow \left( {x + 8} \right)\left( {\sqrt {x + 7} - 3} \right) - \left( {{x^2} + 7x - 18} \right) = 0\\ \Leftrightarrow \left( {x - 2} \right)\frac{{x + 8}}{{\sqrt {x + 7} + 3}} - \left( {x - 2} \right)\left( {x + 9} \right) = 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {\frac{{x + 8}}{{\sqrt {x + 7} + 3}} - x - 9} \right) = 0\,\,\,\,\left( * \right)\end{array}\) Với mọi \(x \ge - 7\), ta có: \(\frac{{x + 8}}{{\sqrt {x + 7} + 3}} - x - 9 = \frac{{x + 8}}{{\sqrt {x + 7} + 3}} - \left( {x + 8} \right) - 1 < 0\) \( \Rightarrow \left( * \right) \Leftrightarrow x - 2 = 0 \Leftrightarrow x = 2.\) Vậy phương trình có nghiệm \(x = 2\). Chọn C. Câu hỏi 17 : Giải phương trình \({x^2} + 2x + 2x\sqrt {x + 3} = 6\sqrt {1 - x} + 7.\)
Đáp án: D Phương pháp giải: Tách bình phương sau đó nhân liên hợp giải phương trình vô tỉ. Lời giải chi tiết: Điều kiện xác định: \( - 3 \le x \le 1.\) \(\begin{array}{l}\,\,\,\,\,\,{x^2} + 2x + 2x\sqrt {x + 3} = 6\sqrt {1 - x} + 7\\ \Leftrightarrow {x^2} + 2x\sqrt {x + 3} + x + 3 = 1 - x + 6\sqrt {1 - x} + 9\\ \Leftrightarrow {\left( {x + \sqrt {x + 3} } \right)^2} = {\left( {\sqrt {1 - x} + 3} \right)^2}\\ \Leftrightarrow \left[ \begin{array}{l}x + \sqrt {x + 3} = \sqrt {1 - x} + 3\,\,\,\,\,\,\,\left( 1 \right)\\x + \sqrt {x + 3} = - \sqrt {1 - x} - 3\,\,\,\left( 2 \right)\end{array} \right..\end{array}\) \(\left( 2 \right) \Leftrightarrow x + 3 + \sqrt {x + 3} + \sqrt {1 - x} = 0\), vô nghiệm với \( - 3 \le x \le 1.\) \(\begin{array}{l}\left( 1 \right) \Leftrightarrow \left( {x - 1} \right) - \sqrt {1 - x} + \left( {\sqrt {x + 3} - 2} \right) = 0\\\,\,\,\,\,\,\, \Leftrightarrow \left( {x - 1} \right) - \sqrt {1 - x} + \frac{{x - 1}}{{\sqrt {x + 3} + 2}} = 0\\\,\,\,\,\,\, \Leftrightarrow \sqrt {1 - x} \left( { - \sqrt {1 - x} - 1 - \frac{{\sqrt {1 - x} }}{{\sqrt {x + 3} + 2}}} \right) = 0\\\,\,\,\,\,\, \Leftrightarrow 1 - x = 0\,\,\,\,\,\,\left( {do\,\,\,\, - \sqrt {1 - x} - 1 - \frac{{\sqrt {1 - x} }}{{\sqrt {x + 3} + 2}} < 0} \right)\\\,\,\,\,\,\, \Leftrightarrow x = 1\,\,\,\left( {tm} \right).\end{array}\) Vậy \(x = 1\) là nghiệm duy nhất của phương trình. Chọn D. Câu hỏi 18 : Gọi \(n\) là số các giá trị cả tham số \(m\) để phương trình \(\frac{{\left( {x + 1} \right)\left( {mx + 2} \right)}}{{x - 2}} = 0\) có nghiệm duy nhất. Tìm \(n\).
Đáp án: D Phương pháp giải: Biện luận phương trình bậc nhất. Lời giải chi tiết: ĐKXĐ: \(x \ne 2.\) Ta có: \(\frac{{\left( {x + 1} \right)\left( {mx + 2} \right)}}{{x - 2}} = 0\,\,\,\,\left( * \right) \Leftrightarrow \left( {x + 1} \right)\left( {mx + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\mx + 2 = 0\,\,\,\,\,\left( 1 \right)\end{array} \right.\,\,\,\,\) Phương trình \(\left( * \right)\) có nghiệm duy nhất khi xảy ra một trong ba trường hợp sau: TH1: Phương trình \(mx + 2 = 0\) vô nghiệm \( \Leftrightarrow m = 0.\) TH2: Phương trình \(mx + 2 = 0\) có nghiệm \(x = - 1 \Leftrightarrow - m + 2 = 0 \Leftrightarrow m = 2.\) TH3: Phương trình \(mx + 2 = 0\) có nghiệm \(x = 2 \Leftrightarrow 2m + 2 = 0 \Leftrightarrow m = - 1.\) Vậy có ba giá trị của \(m\) thỏa mãn đề bài \( \Rightarrow n = 3.\) Chọn D. Câu hỏi 19 : Giải phương trình \(8{x^2} + 11x + 1 = \left( {x + 1} \right)\sqrt {4{x^2} + 6x + 5} .\)
Đáp án: B Phương pháp giải: Giải phương trình bằng phương pháp bình phương hai vế sau đó đưa về dạng phương trình tích. Lời giải chi tiết: TXĐ:\(D = \mathbb{R}.\) \(\begin{array}{l}\,\,\,\,\,\,\,8{x^2} + 11x + 1 = \left( {x + 1} \right)\sqrt {4{x^2} + 6x + 5} \\ \Rightarrow {\left( {8{x^2} + 11x + 1} \right)^2} = \left( {{x^2} + 2x + 1} \right)\left( {4{x^2} + 6x + 5} \right)\\ \Leftrightarrow 64{x^4} + 121{x^2} + 1 + 176{x^3} + 16{x^2} + 22x = 4{x^4} + 14{x^3} + 21{x^2} + 16x + 5\\ \Leftrightarrow 60{x^4} + 162{x^3} + 116{x^2} + 6x - 4 = 0\\ \Leftrightarrow 2\left( {5{x^2} + 6x - 1} \right)\left( {6{x^2} + 9x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}5{x^2} + 6x - 1 = 0\\6{x^2} + 9x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{ - 3 + \sqrt {14} }}{5}\\x = \frac{{ - 3 - \sqrt {14} }}{5}\\x = \frac{{ - 9 + \sqrt {33} }}{{12}}\\x = \frac{{ - 9 - \sqrt {33} }}{{12}}\end{array} \right..\end{array}\)\(\) Thử lại các nghiệm tìm được vào phương trình ta được nghiệm của phương trình là \(S = \left\{ {\frac{{ - 3 + \sqrt {14} }}{5};\frac{{ - 9 - \sqrt {33} }}{{12}}} \right\}.\) Chọn B. Câu hỏi 20 : Biết phương trình \({x^2} - 2mx - 1 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn biểu thức \(S = \left( {x_1^2 - 1} \right)\left( {x_2^2 - 4} \right)\) đạt giá trị lớn nhất. Tính giá trị lớn nhất đó.
Đáp án: D Phương pháp giải: Sử dụng bất thẳng thức \(2ab \le {a^2} + {b^2}\) tìm giá trị lớn nhất. Lời giải chi tiết: \({x^2} - 2mx - 1 = 0\). \(\Delta ' = {m^2} + 1 > 0,\forall m\) nên phương trình luôn có hai nghiệm phân biệt. \(x = m \pm \sqrt {{m^2} + 1} .\) Vì \({x_1},{x_2}\) là nghiệm của phương trình nên: \(\begin{array}{l}\left\{ \begin{array}{l}x_1^2 - 2m{x_1} - 1 = 0\\x_2^2 - 2m{x_2} - 1 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x_1^2 - 1 = 2m{x_1}\\x_2^2 - 4 = 2m{x_2} - 3\end{array} \right.\\ \Rightarrow S = \left( {x_1^2 - 1} \right)\left( {x_2^2 - 4} \right) = 2m{x_1}\left( {2m{x_2} - 3} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = 4{m^2}{x_1}{x_2} - 6m{x_1} = - 4{m^2} - 6m{x_1}\\\,\,\,\,\,\,\,\,\,\,\,\, = - 4{m^2} - 6m\left( {m \pm \sqrt {{m^2} + 1} } \right).\end{array}\) Trường hợp 1: \(S = - 4{m^2} - 6m\left( {m + \sqrt {{m^2} + 1} } \right)\)\( = - 10{m^2} - 6m\sqrt {{m^2} + 1} .\) Áp dụng bất đẳng thức \(2ab \le {a^2} + {b^2}\) ta có: \( - 6m\sqrt {{m^2} + 1} = 2.\left( { - 3m} \right).\sqrt {{m^2} + 1} \le 9{m^2} + {m^2} + 1 = 10{m^2} + 1\) \( \Rightarrow S \le - 10{m^2} + 10{m^2} + 1 = 1.\) Trường hợp 2: \(S = - 4{m^2} - 6m\left( {m - \sqrt {{m^2} + 1} } \right)\)\( = - 10{m^2} + 6m\sqrt {{m^2} + 1} .\) Áp dụng bất đẳng thức \(2ab \le {a^2} + {b^2}\) ta có: \(6m\sqrt {{m^2} + 1} = 2.\left( {3m} \right).\sqrt {{m^2} + 1} \le 9{m^2} + {m^2} + 1 = 10{m^2} + 1\) \( \Rightarrow S \le - 10{m^2} + 10{m^2} + 1 = 1.\) Vậy giá trị lớn nhất của \(S\) là 1, dấu bằng xảy ra khi \(m = \pm \frac{1}{{2\sqrt 2 }}.\) Chọn D. Câu hỏi 21 : Có bao nhiêu giá trị nguyên của tham số m để phương trình \({\left( {{x^2} + 6x + 10} \right)^2} + m = 10{\left( {x + 3} \right)^2}\) có 4 nghiệm phân biệt?
Đáp án: D Phương pháp giải: Biến đổi phương trình, đặt ẩn phụ rồi biện luận phương trình. Lời giải chi tiết: TXĐ: \(D = \mathbb{R}.\) \(\begin{array}{l}\,\,\,\,\,\,{\left( {{x^2} + 6x + 10} \right)^2} + m = 10{\left( {x + 3} \right)^2}\,\,\,\,\\ \Leftrightarrow {\left( {{x^2} + 6x + 9 + 1} \right)^2} - 10{\left( {x + 3} \right)^2} + m = 0\\ \Leftrightarrow {\left[ {{{\left( {x + 3} \right)}^2} + 1} \right]^2} - 10{\left( {x + 3} \right)^2} + m = 0\\ \Leftrightarrow {\left( {x + 3} \right)^4} + 2{\left( {x + 3} \right)^2} + 1 - 10{\left( {x + 3} \right)^2} + m = 0\\ \Leftrightarrow {\left( {x + 3} \right)^4} - 8{\left( {x + 3} \right)^2} + m + 1 = 0\,\,\,\,\,\left( * \right)\end{array}\) Đặt \({\left( {x + 3} \right)^2} = t\,\,\left( {t \ge 0} \right).\) \( \Rightarrow \left( * \right) \Leftrightarrow {t^2} - 8t + m + 1 = 0\,\,\,\,\left( 1 \right)\) \( \Rightarrow \left( * \right)\) có 4 nghiệm phân biệt \( \Leftrightarrow \left( 1 \right)\) có hai nghiệm t dương phân biệt \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\ - \frac{b}{a} > 0\\\frac{c}{a} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}16 - m - 1 > 0\\8 > 0\\m + 1 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}15 - m > 0\\m > - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 15\\m > - 1\end{array} \right. \Leftrightarrow - 1 < m < 15\end{array}\) Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;\,\,1;\,\,2;\,\,.....;\,\,15} \right\}.\) \( \Rightarrow \) Có 16 giá trị m thỏa mãn bài toán. Đáp án D. Câu hỏi 22 : Có nhiều nhất bao nhiêu số nguyên m thuộc nửa khoảng \(\left[ { - 2017;2017} \right)\) để phương trình \(\sqrt {2{x^2} - x - 2m} = x - 2\) có nghiệm ?
Đáp án: A Phương pháp giải: \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\). Lời giải chi tiết:
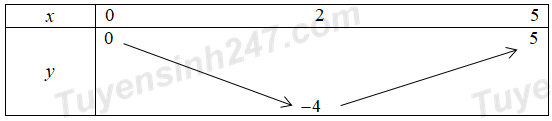
\(\begin{array}{l}\sqrt {2{x^2} - x - 2m} = x - 2\\ \Leftrightarrow \left\{ \begin{array}{l}x - 2 \ge 0\\2{x^2} - x - 2m = {x^2} - 4x + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\{x^2} + 3x - 2m - 4 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\{x^2} + 3x - 4 = 2m\end{array} \right.\end{array}\) Để phương trình ban đầu có nghiệm \( \Leftrightarrow \) phương trình \({x^2} + 3x - 4 = 2m\) có nghiệm \(x \ge 2\). Số nghiệm của phương trình \({x^2} + 3x - 4 = 2m\) là số giao điểm của đồ thị hàm số \(y = {x^2} + 3x - 4\) và đường thẳng \(y = 2m\) song song với trục hoành. Xét hàm số \(y = {x^2} + 3x - 4\) ta có BBT : Dựa vào BBT ta có để phương trình \({x^2} + 3x - 4 = 2m\) có nghiệm \(x \ge 2\) khi và chỉ khi \(2m \ge 6 \Leftrightarrow m \ge 3\). Kết hợp điều kiện đề bài ta có \(m \in \left[ {3;2017} \right)\), có \(\frac{{2016 - 3}}{1} + 1 = 2014\) số nguyên m thỏa mãn. Chọn đáp án A. Câu hỏi 23 : Cho phương trình \({x^2} + 2x - {m^2} = 0.\) Biết rằng có hai giá trị \({m_1},\,\,{m_2}\) của tham số m để phương trình có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^3 + x_2^3 + 10 = 0.\) Tính \({m_1}.{m_2}.\)
Đáp án: B Phương pháp giải: Tìm điều kiện của m để phương trình có hai nghiệm phân biệt. Áp dụng định lý Vi-et để tính giá trị biểu thức, từ đó xác định giá trị của m. Lời giải chi tiết: Phương trình đã cho có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\) \( \Leftrightarrow 1 + {m^2} > 0\,\,\,\forall m\) \( \Rightarrow \) Phương trình đã cho luôn có hai nghiệm phân biệt \({x_1},\,{x_2}\) với mọi m. Áp dụng định lý Vi-et ta có:\(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1}{x_2} = - {m^2}\end{array} \right..\) Theo đề bài ta có: \(x_1^3 + x_2^3 + 10 = 0\) \(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right) + 10 = 0\\ \Leftrightarrow {\left( { - 2} \right)^3} - 3\left( { - {m^2}} \right)\left( { - 2} \right) + 10 = 0\\ \Leftrightarrow - 8 - 6{m^2} + 10 = 0\\ \Leftrightarrow 6{m^2} = 2 \Leftrightarrow {m^2} = \frac{1}{3}\\ \Leftrightarrow \left[ \begin{array}{l}{m_1} = - \frac{1}{{\sqrt 3 }}\\{m_2} = \frac{1}{{\sqrt 3 }}\end{array} \right. \Rightarrow {m_1}{m_2} = - \frac{1}{{\sqrt 3 }}.\frac{1}{{\sqrt 3 }} = - \frac{1}{3}.\end{array}\) Đáp án B. Câu hỏi 24 : Tìm tập nghiệm của phương trình \(\sqrt {3{x^2} - 4x + 4} = 3x + 2\).
Đáp án: A Phương pháp giải: Giải phương trình chứa căn: \(\sqrt A = B \Leftrightarrow \left\{ \begin{array}{l}B \ge 0\\A = {B^2}\end{array} \right.\). Lời giải chi tiết: \(\begin{array}{l}\,\,\,\,\,\,\sqrt {3{x^2} - 4x + 4} = 3x + 2\\ \Leftrightarrow \left\{ \begin{array}{l}3x + 2 \ge 0\\3{x^2} - 4x + 4 = {\left( {3x + 2} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - \frac{2}{3}\\3{x^2} - 4x + 4 = 9{x^2} + 12x + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - \frac{2}{3}\\6{x^2} + 16x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - \frac{2}{3}\\\left[ \begin{array}{l}x = - \frac{8}{3}\\x = 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow x = 0\end{array}\) Vậy tập nghiệm của phương trình là \(S = \left\{ 0 \right\}\). Đáp án A. Câu hỏi 25 : Giải các phương trình: Câu 1: \(\left| {\frac{{{x^2} - 3x + 2}}{2}} \right| = x - 1\)
Đáp án: D Phương pháp giải: \(\left| {f\left( x \right)} \right| = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = \pm g\left( x \right)\end{array} \right.\) Lời giải chi tiết: \(\left| {\frac{{{x^2} - 3x + 2}}{2}} \right| = x - 1\) \( \Leftrightarrow \left\{ \begin{array}{l}x - 1 \ge 0\\\left[ \begin{array}{l}\frac{{{x^2} - 3x + 2}}{2} = x - 1\\\frac{{{x^2} - 3x + 2}}{2} = - x + 1\end{array} \right.\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\\left[ \begin{array}{l}{x^2} - 5x + 4 = 0\\{x^2} - x = 0\end{array} \right.\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\\left[ \begin{array}{l}x = 1\\x = 4\\x = 1\\x = 0\end{array} \right.\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right.\) Vậy phương trình có tập nghiệm \(S = \left\{ {1;4} \right\}.\) Chọn Câu 2: \(6 - \sqrt {3{x^2} - x + 6} = x\)
Đáp án: A Phương pháp giải: \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\) Lời giải chi tiết: \(6 - \sqrt {3{x^2} - x + 6} = x\) \( \Leftrightarrow \sqrt {3{x^2} - x + 6} = 6 - x\) \( \Leftrightarrow \left\{ \begin{array}{l}6 - x \ge 0\\3{x^2} - x + 6 = {\left( {6 - x} \right)^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \le 6\\3{x^2} - x + 6 = {x^2} - 12x + 36\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \le 6\\2{x^2} + 11x - 30 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \le 6\\\left[ \begin{array}{l}x = 2\,\,\,\left( {tm} \right)\\x = - \frac{{15}}{2}\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array} \right..\) Vậy phương trình có tập nghiệm \(S = \left\{ {2; - \frac{{15}}{2}} \right\}.\) Chọn A. Câu hỏi 26 : Cho phương trình \({m^2}x + 1 = x + 3{m^2} - 2m.\) Định \(m\) để phương trình đã cho nghiệm đúng \(\forall x \in \mathbb{R}.\)
Đáp án: A Phương pháp giải: Phương trình \(ax + b = 0\) nghiệm đúng với mọi \(x\) \( \Leftrightarrow a = b = 0\). Lời giải chi tiết: \({m^2}x + 1 = x + 3{m^2} - 2m\) \( \Leftrightarrow \left( {{m^2} - 1} \right)x = 3{m^2} - 2m - 1\) Phương trình đã cho nghiệm đúng \(\forall x \in \mathbb{R}\) \( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 1 = 0\\3{m^2} - 2m - 1 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.\\\left[ \begin{array}{l}m = 1\\m = \frac{{ - 1}}{3}\end{array} \right.\end{array} \right. \Leftrightarrow m = 1\). Vậy \(m = 1\). Chọn A. Câu hỏi 27 : Giải các phương trình sau: Câu 1: \(\left| {2x + 1} \right| = \left| {x - 2} \right|\)
Đáp án: A Phương pháp giải: Giải phương trình dạng \(\left| {A\left( x \right)} \right| = \left| {B\left( x \right)} \right| \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = B\left( x \right)\\A\left( x \right) = - B\left( x \right)\end{array} \right.\) Lời giải chi tiết: \(\left| {2x + 1} \right| = \left| {x - 2} \right|\)\( \Leftrightarrow \left[ \begin{array}{l}2x + 1 = x - 2\\2x + 1 = 2 - x\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = \frac{1}{3}\end{array} \right.\) Vậy tập nghiệm của phương trình \(S = \left\{ { - 3;\frac{1}{3}} \right\}.\) Chọn A. Câu 2: \(\sqrt {2x - 5} = x - 4\)
Đáp án: D Phương pháp giải: Giải phương trình dạng \(\sqrt {A\left( x \right)} = B\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}B\left( x \right) \ge 0\\A\left( x \right) = {\left[ {B\left( x \right)} \right]^2}\end{array} \right.\) Lời giải chi tiết: \(\sqrt {2x - 5} = x - 4\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 4\\2x - 5 = {\left( {x - 4} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 4\\2x - 5 = {x^2} - 8x + 16\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 4\\{x^2} - 10x + 21 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 4\\\left[ \begin{array}{l}x = 3\\x = 7\end{array} \right.\end{array} \right. \Rightarrow x = 7\) Vậy phương trình có nghiệm \(x = 7.\) Chọn D. Câu hỏi 28 : Phương trình \(\left| {3 - x} \right| = \left| {2x - 5} \right|\) có hai nghiệm \({x_1},\,\,{x_2}.\) Tính \({x_1} + {x_2}.\)
Đáp án: D Phương pháp giải: Giải phương trình chứa dấu giá trị tuyệt đối: \(\left| {f\left( x \right)} \right| = g\left( x \right) \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = g\left( x \right)\\f\left( x \right) = - g\left( x \right)\end{array} \right..\) Lời giải chi tiết: Ta có: \(\left| {3 - x} \right| = \left| {2x - 5} \right|\) \(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}3 - x = 2x - 5\\3 - x = - 2x + 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3x = 8\\x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{8}{3}\\x = 2\end{array} \right.\\ \Rightarrow {x_1} + {x_2} = \frac{8}{3} + 2 = \frac{{14}}{3}.\end{array}\) Đáp án D. Câu hỏi 29 : Cho phương trình \(\left( {1 - \sqrt 2 } \right){x^4} - \left( {\sqrt 2 - \sqrt 3 } \right){x^2} + \sqrt 3 = 0\). Số các nghiệm dương của phương trình là
Đáp án: A Phương pháp giải: Đặt \(x^2 = t \ge 0\) rồi đưa về phương trình bậc hai. Từ đó tìm được số nghiệm của phương trình đã cho. Lời giải chi tiết: Đặt \(x^2 = t \ge 0\) ta được phương trình: \(\left( {1 - \sqrt 2 } \right){t^2} - \left( {\sqrt 2 - \sqrt 3 } \right)t + \sqrt 3 = 0\) Phương trình trên có \(ac = \left( {1 - \sqrt 2 } \right).\sqrt 3 < 0\) nên có hai nghiệm trái dấu \({t_1} < 0\left( L \right);{t_2} > 0\left( N \right)\) Thay lại cách đặt ta được \({x^2} = {t_2} \Rightarrow x = \pm \sqrt {{t_2}} \) hay phương trình đã cho có 2 nghiệm phân biệt. Chọn A Câu hỏi 30 : Tìm tất cả các giá trị của tham số \(m\) để phương trình \({x^2} - 4x + 6 + m = 0\) có ít nhất \(1\) nghiệm dương.
Đáp án: A Phương pháp giải: Phương trình có ít nhất một nghiệm dương thì nó có thể có hai nghiệm trái dấu hoặc hai nghiệm đều dương (không nhất thiết phân biệt). Lời giải chi tiết: TH1: Phương trình có hai nghiệm trái dấu \( \Leftrightarrow ac < 0 \Leftrightarrow 1.\left( {m + 6} \right) < 0 \Leftrightarrow m < - 6\). TH2: Phương trình có hai nghiệm dương (không nhất thiết phân biệt) \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\S \ge 0\\P \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - m - 2 \ge 0\\2 > 0\\m + 6 \ge 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m \le - 2\\m \ge - 6\end{array} \right. \Leftrightarrow - 6 \le m \le - 2\). Vậy \(\left[ \begin{array}{l}m < - 6\\ - 6 \le m \le - 2\end{array} \right. \Leftrightarrow m \le - 2.\) Chọn A. Câu hỏi 31 : Các đường thẳng \(y = - 5\left( {x + 2} \right);y = ax + 3;y = 3x + a\) đồng quy với giá trị của \(a\) là:
Đáp án: B Phương pháp giải: Tìm giao điểm của hai đường thẳng rồi thay tọa độ giao điểm đó vào phương trình đường thẳng còn lại. Lời giải chi tiết: Xét các đường thẳng: \(\left( {{d_1}} \right):y = - 5\left( {x + 2} \right);\left( {{d_2}} \right):y = ax + 3;\left( {{d_3}} \right):y = 3x + a\) Để ba đường thẳng trên cắt nhau thì \(a \ne \left\{ { - 5;3} \right\}\) Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_3}} \right)\) ta được: \(\begin{array}{l} - 5\left( {x + 2} \right) = 3x + a \Leftrightarrow - 5x - 10 = 3x + a\\ \Leftrightarrow 8x = - a - 10 \Rightarrow x = \frac{{ - a - 10}}{8} \\ \Rightarrow y = 3.\frac{{ - a - 10}}{8} + a = \frac{{5a - 30}}{8}\end{array}\) Thay \(x = \frac{{ - a - 10}}{8};y = \frac{{5a - 30}}{8}\) vào phương trình đường thẳng \(\left( {{d_2}} \right)\) ta được: \(\begin{array}{l}\frac{{5a - 30}}{8} = a.\frac{{ - a - 10}}{8} + 3\\ \Leftrightarrow 5a - 30 = - {a^2} - 10a + 24\\ \Leftrightarrow {a^2} + 15a - 54 = 0\\ \Leftrightarrow \left[ \begin{array}{l}a = - 18\left( {tm} \right)\\a = 3\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy \(a = - 18.\) Chọn B Câu hỏi 32 : Giải phương trình \(\left| {x - 2} \right| = {x^2} - 3x - 4.\)
Đáp án: D Phương pháp giải: Phá dấu giá trị tuyệt đối và giải phương trình thu được. Lời giải chi tiết: \(\left| {x - 2} \right| = {x^2} - 3x - 4.\) +)\(x \ge 2,\) ta có phương trình \({x^2} - 4x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2 + \sqrt 6 \\x = 2 - \sqrt 6 \,\left( {loai} \right)\end{array} \right.\) +) \(x < 2,\)ta có phương trình \({x^2} - 2x - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 - \sqrt 7 \\x = 1 + \sqrt 7 \,\left( {loai} \right)\end{array} \right.\) Vậy \(S = \left\{ {2 + \sqrt 6 ;\,1 - \sqrt 7 } \right\}\). Chọn D. Câu hỏi 33 : Tìm giá trị của tham số \(m\) để phương trình \({x^4} - \left( {2m + 4} \right){x^2} + 2m + 3 = 0\) có \(4\) nghiệm phân biệt \({x_1},{x_2},{x_3},{x_4}\) thỏa mãn \(\frac{1}{{x_1^2}} + \frac{1}{{x_2^2}} + \frac{1}{{x_3^2}} + \frac{1}{{x_4^2}} - \frac{1}{{{x_1}{x_2}{x_3}{x_4}}} = 5.\)
Đáp án: B Phương pháp giải: Đặt \({x^2} = t\,\,\left( {t \ge 0} \right).\) Phương trình bài cho có 4 nghiệm phân biệt \( \Leftrightarrow \) phương trình ẩn \(t\) có hai nghiệm dương phân biệt. Áp dụng định lý Vi-et và biểu thức bài cho để tìm \(m.\) Lời giải chi tiết: \({x^4} - \left( {2m + 4} \right){x^2} + 2m + 3 = 0 \Leftrightarrow {x^4} - 2\left( {m + 2} \right){x^2} + 2m + 3 = 0\,\,\,\,\,\left( 1 \right)\). Đặt \({x^2} = t\,\,\,\,\left( {t \ge 0} \right)\) phương trình trở thành \({t^2} - 2\left( {m + 2} \right)t + 2m + 3 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\). \(\Delta ' = {\left( {m + 2} \right)^2} - \left( {2m + 3} \right) = {m^2} + 4m + 4 - 2m - 3 = {m^2} + 2m + 1 = {\left( {m + 1} \right)^2}.\) Phương trình \(\left( 1 \right)\) có 4 nghiệm phân biệt \( \Leftrightarrow \,\,\left( 2 \right)\) có 2 nghiệm dương phân biệt \({t_1},\,\,{t_2}\) \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\{t_1} + {t_2} > 0 \Leftrightarrow \left\{ \begin{array}{l}{\left( {m + 1} \right)^2} > 0\\2m + 4 > 0\\2m + 3 > 0\end{array} \right.\\{t_1}{t_2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m + 1 \ne 0\\2m > - 4\\2m > - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 1\\m > - 2\\m > - \frac{3}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 1\\m > - \frac{3}{2}\end{array} \right..\) Khi đó phương trình \(\left( 1 \right)\) có 4 nghiệm phân biệt là: \(\left\{ \begin{array}{l}{x_1} = \sqrt {{t_1}} \\{x_2} = - \sqrt {{t_1}} \\{x_2} = \sqrt {{t_2}} \\{x_2} = - \sqrt {{t_2}} \end{array} \right..\) \(\begin{array}{l}\,\,\,\,\,\,\,\,\frac{1}{{x_1^2}} + \frac{1}{{x_2^2}} + \frac{1}{{x_3^2}} + \frac{1}{{x_4^2}} - \frac{1}{{{x_1}{x_2}{x_3}{x_4}}} = 5\\ \Leftrightarrow \frac{1}{{{t_1}}} + \frac{1}{{{t_1}}} + \frac{1}{{{t_2}}} + \frac{1}{{{t_2}}} - \frac{1}{{\sqrt {{t_1}} .\left( { - \sqrt {{t_1}} } \right).\sqrt {{t_2}} .\left( { - \sqrt {{t_2}} } \right)}} = 5\\ \Leftrightarrow \frac{2}{{{t_1}}} + \frac{2}{{{t_2}}} - \frac{1}{{{t_1}{t_2}}} = 5\\ \Leftrightarrow 2\left( {{t_1} + {t_2}} \right) - 1 = 5{t_1}{t_2}\\ \Leftrightarrow 2\left( {2m + 4} \right) - 1 = 5\left( {2m + 3} \right)\\ \Leftrightarrow 4m + 8 - 1 = 10m + 15\\ \Leftrightarrow 6m = - 8 \Leftrightarrow m = - \frac{4}{3}\,\,\,\left( {tm} \right)\end{array}\) Vậy \(m = - \frac{4}{3}.\) Chọn B. Câu hỏi 34 : Có bao nhiêu giá trị \(m\) nguyên bé hơn \( - 6\) để phương trình \(\sqrt {2{x^2} - 2x - m} = x + 2\) có nghiệm?
Đáp án: C Phương pháp giải: Bình phương hai vế để giải phương trình vô tỉ, kết hợp bảng biến thiên để biện luận số nghiệm. Lời giải chi tiết: \(\sqrt {2{x^2} - 2x - m} = x + 2 \Leftrightarrow \left\{ \begin{array}{l}x + 2 \ge 0\\2{x^2} - 2x - m = {\left( {x + 2} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\2{x^2} - 2x - m = {x^2} + 4x + 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\{x^2} - 6x - 4 = m\end{array} \right..\) Số nghiệm của phương trình đã cho là số giao điểm của đồ thị hàm số \(y = {x^2} - 6x - 4\) và đường thẳng \(y = m\) với \(x \ge - 2.\) Xét hàm số \(y = {x^2} - 6x - 4\) ta có BBT: Từ bảng biến thiên suy ra để phương trình có nghiệm \(x \ge - 2\) thì \(m \ge - 13.\) Lại có:\(\left\{ \begin{array}{l}m \in \mathbb{Z}\\m < - 6\end{array} \right. \Rightarrow \left\{ \begin{array}{l}m \in \mathbb{Z}\\ - 13 \le m < - 6\end{array} \right. \Rightarrow m \in \left\{ { - 13;\, - 12;.....; - 7} \right\} \Rightarrow \) có \(7\) giá trị \(m\) thỏa mãn bài toán. Chọn C. Câu hỏi 35 : Gọi \(T\) là tổng các giá trị của \(m\) để phương trình \({x^2} - \left( {m + 2} \right)x + m + 1 = 0\) có hai nghiệm phân biệt và nghiệm này gấp đôi nghiệm kia. Khi đó \(T\) nhận giá trị:
Đáp án: B Phương pháp giải: Giải và biện luận phương trình bậc hai. Lời giải chi tiết: \({x^2} - \left( {m + 2} \right)x + m + 1 = 0\) \(\Delta = {\left( {m + 2} \right)^2} - 4\left( {m + 1} \right) = {m^2}.\) Phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0 \Leftrightarrow {m^2} > 0 \Leftrightarrow m \ne 0.\) Áp dụng định lý Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 2\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{x_1}{x_2} = m + 1 & \,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right..\) Theo đề bài ta có nghiệm này gấp đôi nghiệm kia, giả sử \({x_2} = 2{x_1}.\) \(\begin{array}{l} \Rightarrow \left( 1 \right) \Leftrightarrow 3{x_1} = m + 2 \Leftrightarrow {x_1} = \frac{{m + 2}}{3}\\ \Rightarrow {x_2} = \frac{{2\left( {m + 2} \right)}}{3} = \frac{{2m + 4}}{3}.\\ \Rightarrow \left( 2 \right) \Leftrightarrow \frac{{m + 2}}{3}.\frac{{2m + 4}}{3} = m + 1\\ \Leftrightarrow 2{m^2} + 8m + 8 = 9m + 9\\ \Leftrightarrow 2{m^2} - m - 1 = 0\\ \Leftrightarrow \left( {2m + 1} \right)\left( {m - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2m + 1 = 0\\m - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - \frac{1}{2}\,\,\,\left( {tm} \right)\\m = 1\,\,\,\,\left( {tm} \right)\end{array} \right..\\ \Rightarrow T = - \frac{1}{2} + 1 = \frac{1}{2}.\end{array}\) Chọn B. Câu hỏi 36 : Tìm giá trị của \(m\) để hai phương trình sau tương đương: \(x - 2 = 0\) và \(\frac{{mx}}{{x - 3}} + 3m - 1 = 0.\)
Đáp án: C Phương pháp giải: Hai phương trình tương đương khi chúng có cùng tập nghiệm. Lời giải chi tiết: \(x - 2 = 0 \Leftrightarrow x = 2.\) \(\frac{{mx}}{{x - 3}} + 3m - 1 = 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 3\\x\left( {4m - 1} \right) = 3\left( {3m - 1} \right)\end{array} \right..\) Điều kiện: \(x \ne 3.\) Phương trình \( \Leftrightarrow mx + \left( {3m - 1} \right)\left( {x - 3} \right) = 0\) \(\begin{array}{l} \Leftrightarrow mx + 3mx - 9m - x + 3 = 0\\ \Leftrightarrow \left( {4m - 1} \right)x = 9m - 3\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\end{array}\) Hai phương trình tương đương \(x = 2\) là nghiệm duy nhất của phương trình \(\left( 1 \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}4m - 1 \ne 0\\2\left( {4m - 1} \right) = 9m - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne \frac{1}{4}\\8m - 2 = 9m - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne \frac{1}{4}\\m = 1\end{array} \right. \Leftrightarrow m = 1.\) Chọn C. Câu hỏi 37 : Tổng \(S\) tất cả các nghiệm của phương trình \(\sqrt {{x^2} + 3x - 2} = \sqrt {1 + x} \) bằng:
Đáp án: D Phương pháp giải: Giải phương trình vô tỉ bằng cách bình phương hai vế. Lời giải chi tiết: \(\begin{array}{l} Chọn D. Câu hỏi 38 : Tập nghiệm của phương trình \(\left( {3{x^2} - 10x + 3} \right)\sqrt {3x - 3} = 0\) là:
Đáp án: B Phương pháp giải: Tìm điều kiện xác định sau đó giải phương trình vô tỉ. Lời giải chi tiết: Điều kiện xác định: \(x \ge 1.\) \(\begin{array}{l}\left( {3{x^2} - 10x + 3} \right)\sqrt {3x - 3} = 0 \Leftrightarrow \left( {x - 3} \right)\left( {3x - 1} \right)\sqrt {3x - 3} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\3x - 1 = 0\\3x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \frac{1}{3}\\x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\,\,\,\left( {do\,\,\,x \ge 1} \right).\end{array}\) Chọn B. Câu hỏi 39 : Có bao nhiêu giá trị \(m\) nguyên, \(m \in \left[ { - 4;4} \right]\) để phương trình \({x^2} + 4mx + {m^2} = 0\) có hai nghiệm âm.
Đáp án: D Phương pháp giải: Giải và biện luận phương trình bậc hai. Lời giải chi tiết: \({x^2} + 4mx + {m^2} = 0\) có \(\Delta ' = 4{m^2} - {m^2} = 3{m^2} \ge 0,\forall m\) nên phương trình luôn có hai nghiệm. Phương trình có hai nghiệm âm \( \Leftrightarrow \left\{ \begin{array}{l}{x_1} + {x_2} = - 2m < 0\\{x_1}{x_2} = {m^2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m \ne 0\end{array} \right. \Leftrightarrow m > 0.\) Vì \(m \in \left[ { - 4;4} \right]\) và \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {1;\,\,2;\,\,3;\,\,4} \right\}\) thỏa mãn yêu cầu bài toán. Chọn D. Câu hỏi 40 : Tìm tất cả các giá trị của tham số \(m\) để phương trình \(\left| {2x - 3} \right| = \left| {mx + 1} \right|\) có hai nghiệm dương phân biệt
Đáp án: D Phương pháp giải: Giải và biện luận phương trình chứa dấu giá trị tuyệt đối. Lời giải chi tiết: \(\left| {2x - 3} \right| = \left| {mx + 1} \right| \Leftrightarrow \left[ \begin{array}{l}2x - 3 = mx + 1\\2x - 3 = - mx - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left( {m - 2} \right)x = - 4\\\left( {m + 2} \right)x = 2\end{array} \right..\) Phương trình đã cho có hai nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}m \ne \pm 2\\\frac{{ - 4}}{{m - 2}} > 0\\\frac{2}{{m + 2}} > 0\\\frac{{ - 4}}{{m - 2}} \ne \frac{2}{{m + 2}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne \pm 2\\m - 2 < 0\\m + 2 > 0\\ - 2\left( {m + 2} \right) \ne m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 2\\m > - 2\\3m \ne - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2 < m < 2\\m \ne - \frac{2}{3}\end{array} \right..\) Chọn B.
|