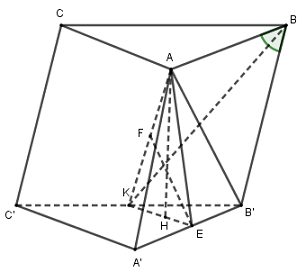
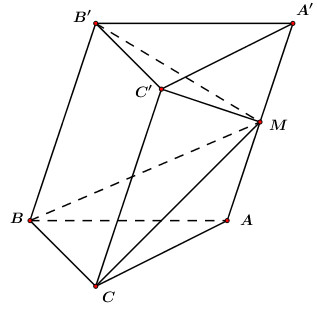
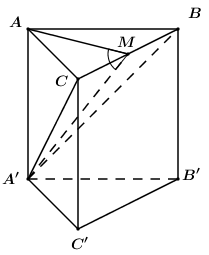
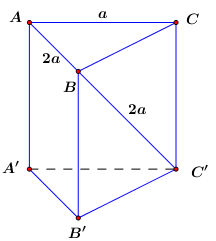
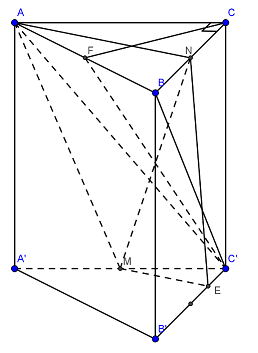
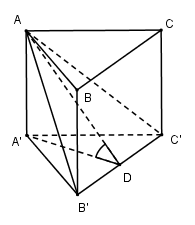
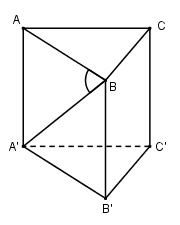
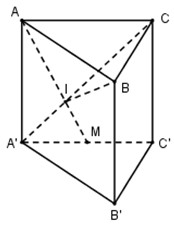
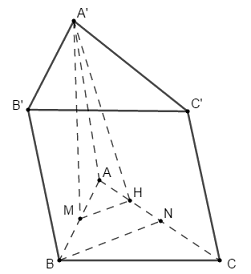
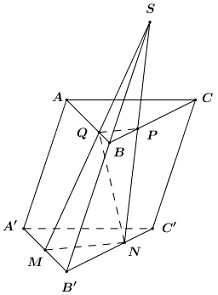
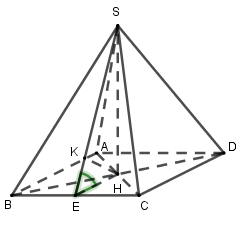
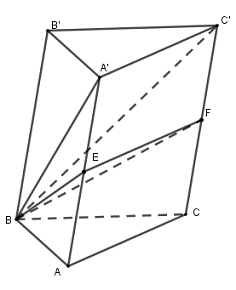
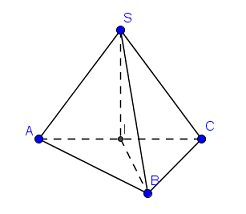
50 bài tập trắc nghiệm thể tích khối đa diện mức độ vận dụngLàm bàiCâu hỏi 1 : Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A\) với \(AB = 2;\)\(BC = 4\). Mặt bên \(ABB'A'\) là hình thoi có góc \(B\) bằng \({60^0}\). Gọi điểm \(K\) là trung điểm của \(B'C'\). Tính thể tích khối lăng trụ biết \(d\left( {A'B';BK} \right) = \dfrac{3}{2}\).
Đáp án: C Phương pháp giải: Sử dụng lý thuyết: - Cho hai đường thẳng chéo nhau \(a,b\). Mặt phẳng \(\left( P \right)\) chứa \(b\) và song song với \(a\). Khi đó, \(d\left( {a,b} \right) = d\left( {a,\left( P \right)} \right)\). - Thể tích khối lăng trụ \(V = Bh\) với \(B\) là diện tích đáy, \(h\) là chiều cao. Lời giải chi tiết:
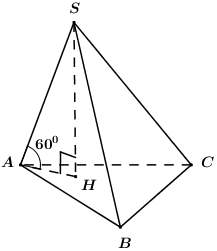
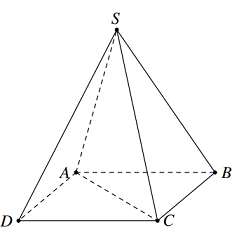
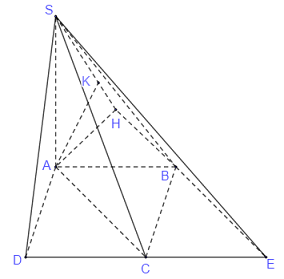
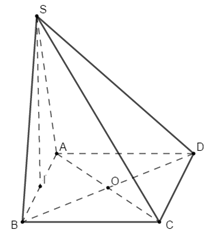
Tam giác \(AA'B\) có \(AA' = A'B\) và \(\widehat {A'} = \widehat B = {60^0}\) nên là tam giác đều cạnh \(2\). Tam giác ABC vuông tại A có \(AB = 2,BC = 4\) nên theo Pitago ta có : \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{4^2} - {2^2}} = 2\sqrt 3 \)\( \Rightarrow A'C' = AC = 2\sqrt 3 \). Gọi E là trung điểm của A’B’ ta thấy, AE là đường cao trong tam giác đều AA’B cạnh \(2\) nên \(AE = \dfrac{{2\sqrt 3 }}{2} = \sqrt 3 \) KE là đường trung bình trong tam giác B’C’A’ nên \(KE = \dfrac{1}{2}A'C' = \dfrac{1}{2}.2\sqrt 3 = \sqrt 3 \) Do đó tam giác AEK cân tại E. Ta thấy, \(A'B'//AB \subset \left( {ABK} \right)\)\( \Rightarrow d\left( {A'B',BK} \right) = d\left( {A'B',\left( {ABK} \right)} \right)\) (1) Mà \(AK \subset \left( {ABK} \right)\)\( \Rightarrow d\left( {A'B',AK} \right) = d\left( {A'B',\left( {ABK} \right)} \right)\) (2) Từ (1) và (2) suy ra \(d\left( {A'B',BK} \right) = d\left( {A'B',AK} \right) = \dfrac{3}{2}\). Gọi F là trung điểm của AK thì \(EF \bot AK\) (3) Lại có, \(\left\{ \begin{array}{l}AE \bot A'B'\\KE \bot A'B'\end{array} \right.\)\( \Rightarrow A'B' \bot \left( {AKE} \right) \Rightarrow A'B' \bot EF\) (4) Do đó EF là đoạn vuông góc chung của hai đường thẳng A’B’ và AK \( \Rightarrow d\left( {A'B',AK} \right) = EF = \dfrac{3}{2}\). Tam giác AEF vuông tại F có \(AE = \sqrt 3 ,EF = \dfrac{3}{2}\) nên theo Pitago ta có : \(AF = \sqrt {A{E^2} - E{F^2}} = \sqrt {{{\left( {\sqrt 3 } \right)}^2} - {{\left( {\dfrac{3}{2}} \right)}^2}} = \dfrac{{\sqrt 3 }}{2}\)\( \Rightarrow AK = 2AF = 2.\dfrac{{\sqrt 3 }}{2} = \sqrt 3 \) Tam giác AKE có \(AE = EK = AK = \sqrt 3 \) nên là tam giác đều. Gọi H là hình chiếu của A lên KE thì : \(AH \bot KE\) và \(AH = EF = \dfrac{3}{2}\) (đường cao trong tam giác đều cạnh \(\sqrt 3 \)). Mà \(A'B' \bot \left( {AKE} \right) \Rightarrow A'B' \bot AH\) Do đó \(AH \bot \left( {A'B'C'} \right)\). Vậy \({V_{ABC.A'B'C'}} = {S_{ABC}}.AH = \dfrac{1}{2}AB.AC.AH\)\( = \dfrac{1}{2}.2.2\sqrt 3 .\dfrac{3}{2} = 3\sqrt 3 \). Chọn C. Câu hỏi 2 : Cho hình chóp \(S.ABC\) có đáy là tam giác cân tại \(A\), mặt bên \(\left( {SBC} \right)\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi \(\left( \alpha \right)\) là mặt phẳng đi qua điểm \(B\) và vuông góc với \(SC\), chia khối chóp thành hai phần. Tính tỉ số thể tích của hai phần đó.
Đáp án: A Phương pháp giải: - Gọi D là trung điểm của BC. Chứng minh \(AD \bot SC\). Từ đó, dựng mặt phẳng \(\left( \alpha \right)\) với chú ý \(\left( \alpha \right)//AD\). - Sử dụng tỉ số thể tích khối chóp \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\) Lời giải chi tiết:
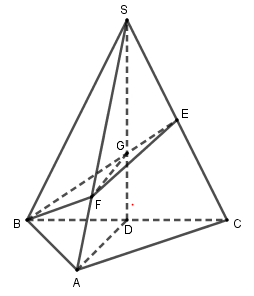
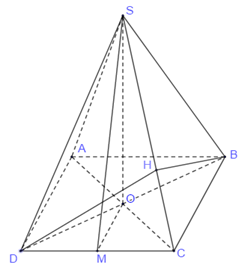
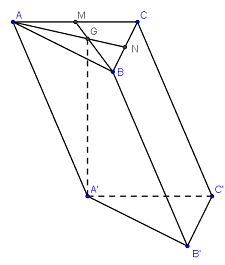
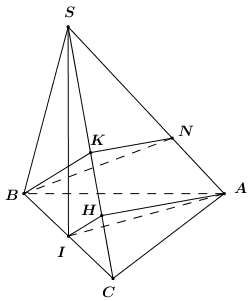
Gọi D là trung điểm của BC ta có \(AD \bot BC\) Mà \(\left( {SBC} \right) \bot \left( {ABC} \right),AD \subset \left( {ABC} \right)\) nên \(AD \bot \left( {SBC} \right)\)\( \Rightarrow AD \bot SC\) Lại có \(\left( \alpha \right) \bot SC \Rightarrow \left( \alpha \right)//AD\) Gọi E là trung điểm của SC thì \(BE \bot SC \Rightarrow BE \subset \left( \alpha \right)\) Trong mp(SBC), gọi G là giao điểm của BE và AD thì \(G \in BE \subset \left( \alpha \right)\) Tròn mp(SAD), qua G kẻ GF//AD (\(F \in SA\)) ta được (BEF) chính là mặt phẳng \(\left( \alpha \right)\). Dễ thấy G là trọng tâm tam giác SBC nên \(\dfrac{{SG}}{{SD}} = \dfrac{2}{3}\). Mà GF//AD nên theo Ta let \(\dfrac{{SF}}{{SA}} = \dfrac{{SG}}{{SD}} = \dfrac{2}{3}\) Vậy \(\dfrac{{{V_{S.BEF}}}}{{{V_{S.BCA}}}} = \dfrac{{SB}}{{SB}}.\dfrac{{SE}}{{SC}}.\dfrac{{SF}}{{SA}} = 1.\dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{3}\). \(\begin{array}{l} \Rightarrow {V_{S.BEF}} = \dfrac{1}{3}{V_{S.ABC}}\\ \Rightarrow {V_{B.ACEF}} = {V_{S.ABC}} - {V_{S.BEF}}\\ = {V_{S.ABC}} - \dfrac{1}{3}{V_{S.ABC}} = \dfrac{2}{3}{V_{S.ABC}}\\ \Rightarrow \dfrac{{{V_{S.BEF}}}}{{{V_{B.ACEF}}}} = \dfrac{{\dfrac{1}{3}{V_{S.ABC}}}}{{\dfrac{2}{3}{V_{S.ABC}}}} = \dfrac{1}{2}\end{array}\) Chọn A. Câu hỏi 3 : Cho hình chóp đều \(S.ABC\), góc giữa mặt bên và mặt phẳng đáy \(\left( {ABC} \right)\) bằng \({60^0}\), khoảng cách giữa hai đường thẳng \(SA\) và \(BC\) bằng \(\dfrac{{3a}}{{2\sqrt 7 }}\). Thể tích của khối chóp \(S.ABC\) theo \(a\) bằng:
Đáp án: D Phương pháp giải: - Gọi \(O\) là tâm tam giác đều \(ABC\) \( \Rightarrow SO \bot \left( {ABC} \right)\). - Gọi \(N\) là trung điểm \(BC\), chứng minh \(\angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SN;AN} \right)\). - Đặt \(ON = x\), tính \(SO,\,\,SA\) theo \(x\), sử dụng tỉ số lượng giác và định lí Pytago trong tam giác vuông. - Sử dụng hệ thức: \(SO.AN = NH.SA\), tính \(x\) theo \(a\). Từ đó tính được \(AB\) và tính được \({S_{\Delta ABC}} = \dfrac{{A{B^2}\sqrt 3 }}{4}\). - Tính thể tích \({V_{S.ABC}} = \dfrac{1}{3}SO.{S_{\Delta ABC}}\). Lời giải chi tiết:
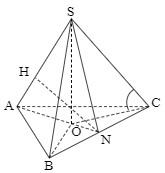
+ Gọi \(O\) là tâm tam giác đều \(ABC\) \( \Rightarrow SO \bot \left( {ABC} \right)\). + Gọi \(N\) là trung điểm \(BC\) ta có: \(\left\{ \begin{array}{l}BC \bot AN\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SAN} \right) \Rightarrow BC \bot SN\). + \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\SN \subset \left( {SBC} \right),\,\,SN \bot BC\\AN \subset \left( {ABC} \right),\,\,AN \bot BC\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SN;AN} \right) = \angle SNA = {60^0}\). + Trong \(\left( {SAM} \right)\) kẻ \(NH \bot SA\,\,\left( {H \in SA} \right)\) \( \Rightarrow NH \bot BC\) \( \Rightarrow d\left( {SA;BC} \right) = NH = \dfrac{{3a}}{{2\sqrt 7 }}\). + Đặt \(ON = x \Rightarrow AN = 3x,\,\,OA = 2x\). + \(\Delta SON:\,\,SO = ON.\tan {60^0} = x\sqrt 3 \), \(SA = \sqrt {S{O^2} + O{A^2}} = \sqrt {3{x^2} + 4{x^2}} = x\sqrt 7 \). + \(\Delta SAN:\,\,{S_{\Delta SAN}} = \dfrac{1}{2}SO.AN = \dfrac{1}{2}NH.SA\) \(\begin{array}{l} \Rightarrow SO.AN = NH.SA\\ \Rightarrow x\sqrt 3 .3x = \dfrac{{3a}}{{2\sqrt 7 }}.x\sqrt 7 \\ \Leftrightarrow x = \dfrac{a}{{2\sqrt 3 }}\end{array}\) \(\begin{array}{l} \Rightarrow AM = 3a = \dfrac{{a\sqrt 3 }}{2} = \dfrac{{AB\sqrt 3 }}{2} \Rightarrow AB = a\\ \Rightarrow {S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\end{array}\) Và \(SO = x\sqrt 3 = \dfrac{a}{2}\). Vậy \({V_{S.ABC}} = \dfrac{1}{3}SO.{S_{\Delta ABC}} = \dfrac{1}{3}.\dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{24}}\). Chọn D. Câu hỏi 4 : Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\), điểm \(M\) là trung điểm cạnh \(BC\) và \(I\) là tâm hình vuông \(CDD'C'\). Mặt phẳng \(\left( {AMI} \right)\) chia khối lập phương thành hai khối đa diện, trong đó khối đa diện không chứa điểm \(D\) có thể tích là \(V\). Khi đó giá trị của \(V\) là:
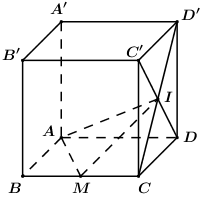
Đáp án: D Phương pháp giải: - Xác định thiết diện của khối lập phương cắt bởi \(\left( {AMI} \right)\). - Chứng minh \(V = {V_{ABCD.A'B'C'D'}} - {V_{CDAMNP}} = {a^3} - {V_1}\). - Phân chia khối đa diện: \({V_1} = {V_{D.APE}} - {V_{C.MNE}}\). - Sử dụng định lí Ta-lét, định lí Menelaus tính độ dài các cạnh, từ đó tính thể tích các khối tứ diên vuông \({V_{D.APE}};\,\,{V_{C.MNE}}\). Lời giải chi tiết: Trong \(\left( {ABCD} \right)\) kéo dài \(AM \cap CD = \left\{ E \right\}\). Trong \(\left( {CDD'C'} \right)\) kéo dài \(EI\) cắt \(CC',\,\,DD'\) lần lượt tại \(N,\,\,P\). Khi đó \(\left( {AMI} \right)\) cắt khối lập phương \(ABCD.A'B'C'D'\) theo thiết diện là tứ giác \(AMNP\) và thể tích khối đa diện không chứa điểm \(D\) là \(V = {V_{ABCD.A'B'C'D'}} - {V_{CDAMNP}} = {a^3} - {V_1}\). Ta có \({V_1} = {V_{D.APE}} - {V_{C.MNE}}\). Áp dụng định lí Ta-lét ta có: \(\dfrac{{MC}}{{AD}} = \dfrac{{EM}}{{EA}} = \dfrac{{EC}}{{ED}} = \dfrac{1}{2}\) nên \(M,\,\,C\) lần lượt là trung điểm của \(AE\) và \(DE\). Khi đó ta có \(CE = CD = a,\,\,DE = 2CD = 2a\). Áp dụng định lí Menelaus trong tam giác \(DD'E\) có: \(\dfrac{{PD}}{{PD'}}.\dfrac{{ID'}}{{IC}}.\dfrac{{EC}}{{ED}} = 1\) \( \Leftrightarrow \dfrac{{PD}}{{PD'}}.1.\dfrac{1}{2} = 1 \Leftrightarrow \dfrac{{PD}}{{PD'}} = 2\). \( \Rightarrow PD = \dfrac{2}{3}DD' = \dfrac{{2a}}{3}\). Áp dụng định lí Ta-lét ta có: \(\dfrac{{NC}}{{PD}} = \dfrac{{EC}}{{ED}} = \dfrac{1}{2}\) \( \Rightarrow NC = \dfrac{1}{2}PD = \dfrac{a}{3}\). \(\begin{array}{l} \Rightarrow {V_{D.APE}} = \dfrac{1}{6}DP.DA.DE = \dfrac{1}{6}.\dfrac{{2a}}{3}.a.2a = \dfrac{{2{a^3}}}{9}\\\,\,\,\,\,\,{V_{C.MNE}} = \dfrac{1}{6}.CN.CM.CE = \dfrac{1}{6}.\dfrac{a}{3}.\dfrac{a}{2}.a = \dfrac{{{a^3}}}{{36}}\end{array}\) \( \Rightarrow {V_1} = {V_{D.APE}} - {V_{C.MNE}} = \dfrac{{2{a^3}}}{9} - \dfrac{{{a^3}}}{{36}} = \dfrac{{7{a^3}}}{{36}}\). Vậy \(V = {a^3} - {V_1} = {a^3} - \dfrac{{7{a^3}}}{{36}} = \dfrac{{29{a^3}}}{{36}}\). Chọn D. Câu hỏi 5 : Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng \(4\) và tạo với đáy góc \({60^0}\). Thể tích của khối chóp đó là:
Đáp án: D Phương pháp giải: - Sử dụng định lí Pytago đảo chứng minh đáy là tam giác vuông, từ đó tính diện tích đáy. - Xác định góc giữa cạnh bên và mặt đáy là góc giữa cạnh bên và hình chiếu của cạnh bên đó trên mặt đáy, từ đó sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính chiều cao của khối chóp. - Sử dụng công thức tính thể tích khối chóp có chiều cao \(h\), diện tích đáy \(B\) là \(V = \dfrac{1}{3}Bh\). Lời giải chi tiết: Xét tam giác \(ABC\), giả sử \(AB = 6,\,\,BC = 8,\,\,AC = 10\) ta có \(A{B^2} + B{C^2} = A{C^2}\,\,\left( { = 100} \right)\) nên tam giác \(ABC\) vuông tại \(B\) (định lí Pytago đảo) \( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}.6.8 = 24\). Gọi \(H\) là hình chiếu vuông góc của \(S\) lên \(\left( {ABC} \right)\) và giả sử \(SA\) hợp với đáy góc \({60^0}\) \( \Rightarrow HA\) là hình chiếu của \(SA\) lên \(\left( {ABC} \right)\) nên \(\angle \left( {SA;\left( {ABC} \right)} \right) = \angle \left( {SA;HA} \right) = \angle SAH = {60^0}\). \( \Rightarrow SH = SA.\sin {60^0} = 4.\dfrac{{\sqrt 3 }}{2} = 2\sqrt 3 \). Vậy \({V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}} = \dfrac{1}{3}.2\sqrt 3 .24 = 16\sqrt 3 \). Chọn D. Câu hỏi 6 : Cho hình lăng trụ \(ABC.A'B'C',\) \(M\) là trung điểm của \(AA'.\) Biết thể tích khối chóp \(M.BB'C'C\) bằng \(V.\) Khi đó thể tích khối lăng trụ bằng
Đáp án: C Phương pháp giải: Thể tích khối lăng trụ có diện tích đáy \(S\) và chiều cao \(h\) là: \(V = Sh.\) Thể tích khối chóp có diện tích đáy \(S\) và chiều cao \(h\) là: \(V = \dfrac{1}{3}Sh.\) Ta có: \({V_{ABC.A'B'C'}} = {V_{M.A'B'C'}} + {V_{M.ABC}} + {V_{M.BCC'B'}}.\) Lời giải chi tiết:
Ta có: \({V_{ABC.A'B'C'}} = {V_{M.A'B'C'}} + {V_{M.ABC}} + {V_{M.BCC'B'}}\) \(\begin{array}{l} \Leftrightarrow {V_{ABC.A'B'C'}} = 2{V_{MABC}} + V = 2.\dfrac{1}{3}d\left( {M;\,\,\left( {ABC} \right)} \right).{S_{ABC}} + V\\ \Leftrightarrow {V_{ABC.A'B'C'}} = 2.\dfrac{1}{3}.\dfrac{1}{2}d\left( {A';\,\,\left( {ABC} \right)} \right).{S_{ABC}} + V\\ \Leftrightarrow {V_{ABC.A'B'C'}} = \dfrac{1}{3}{V_{ABC.A'B'C'}} + V\\ \Rightarrow \dfrac{2}{3}{V_{ABC.A'B'C'}} = V\\ \Leftrightarrow {V_{ABC.A'B'C'}} = \dfrac{3}{2}V.\end{array}\) Chọn C. Câu hỏi 7 : Cho khối lập phương \(ABCD.A'B'C'D'\) có độ dài một cạnh là \(a\). Gọi \(M\) là điểm thuộc cạnh \(BB'\) sao \(BM = 2MB'\), \(K\) là trung điểm \(DD'\). Mặt phẳng \(\left( {CMK} \right)\) chia khối lập phương thành hai khối đa diện, tính theo \(a\) thể tích \({V_1}\) của khối đa diện chứa đỉnh \(C'\).
Đáp án: D Phương pháp giải: - Xác định thiết diện của hình lập phương cắt bởi \(\left( {CMK} \right)\). - Phân chia và lắp ghép các khối đa diện. Lời giải chi tiết:
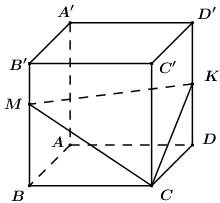
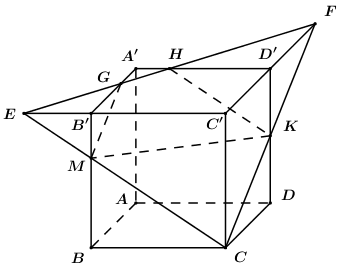
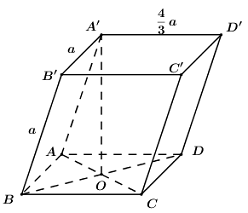
Trong \(\left( {BCC'B'} \right)\) kéo dài \(CM\) cắt \(B'C'\) tại \(E\), trong \(\left( {CDD'C'} \right)\) kéo dài \(CK\) cắt \(C'D'\) tại \(F\). Trong \(\left( {A'B'C'D'} \right)\) nối \(EF\) cắt \(A'B',\,\,A'D'\) lần lượt tại \(G,\,\,H\). Khi đó thiết diện của khối lập phương cắt bởi \(\left( {CMK} \right)\) là ngũ giác \(CMGHK\) và \({V_1} = {V_{C.C'EF}} - {V_{M.B'EG}} - {V_{K.D'HF}}\) Áp dụng định lí Ta-lét ta có: \(\dfrac{{EB'}}{{EC'}} = \dfrac{{B'M}}{{CC'}} = \dfrac{1}{3}\) \( \Rightarrow EB' = \dfrac{1}{3}EC' \Rightarrow EB' = \dfrac{1}{2}B'C' = \dfrac{a}{2}\). \(\dfrac{{FD'}}{{FC'}} = \dfrac{{D'K}}{{CC'}} = \dfrac{1}{2}\) \( \Rightarrow D'\) là trung điểm của \(C'F\) nên \(C'F = 2a,\,\,D'F = a\). \(\dfrac{{B'G}}{{C'F}} = \dfrac{{EB'}}{{EC'}} = \dfrac{1}{3}\) \( \Rightarrow B'G = \dfrac{1}{3}C'F = \dfrac{{2a}}{3}\) \( \Rightarrow A'G = A'B' - B'G = \dfrac{a}{3}\). Ta có \(\dfrac{{EB'}}{{EC'}} = \dfrac{1}{3} \Rightarrow \dfrac{{B'C'}}{{EC'}} = \dfrac{2}{3} \Rightarrow EC' = \dfrac{{3a}}{2}\). \(\dfrac{{HD'}}{{EC'}} = \dfrac{{FD'}}{{FC'}} = \dfrac{1}{2} \Rightarrow HD' = \dfrac{1}{2}EC' = \dfrac{{3a}}{4}\) \( \Rightarrow A'H = A'D' - HD' = \dfrac{a}{4}\). Khi đó ta có: \({S_{C'EF}} = \dfrac{1}{2}C'E.C'F = \dfrac{1}{2}.\dfrac{{3a}}{2}.2a = \dfrac{{3{a^2}}}{2}\) \( \Rightarrow {V_{C.C'EF}} = \dfrac{1}{3}CC'.{S_{C'EE}} = \dfrac{1}{3}.a.\dfrac{{3{a^2}}}{2} = \dfrac{{{a^3}}}{2}\). \({S_{B'EG}} = \dfrac{1}{2}B'E.B'G = \dfrac{1}{2}.\dfrac{a}{2}.\dfrac{{2a}}{3} = \dfrac{{{a^2}}}{6}\) \( \Rightarrow {V_{M.B'EG}} = \dfrac{1}{3}MB'.{S_{B'EG}} = \dfrac{1}{3}.\dfrac{a}{3}.\dfrac{{{a^2}}}{6} = \dfrac{{{a^3}}}{{54}}\). \({S_{D'HF}} = \dfrac{1}{2}D'H.D'F = \dfrac{1}{2}.\dfrac{{3a}}{4}.a = \dfrac{{3{a^2}}}{8}\)\( \Rightarrow {V_{K.D'HF}} = \dfrac{1}{3}.KD'.{S_{D'HF}} = \dfrac{1}{3}.\dfrac{a}{2}.\dfrac{{3{a^2}}}{8} = \dfrac{{{a^3}}}{{16}}\). Vậy \({V_1} = {V_{C.C'EF}} - {V_{M.B'EG}} - {V_{K.D'HF}} = \dfrac{{{a^3}}}{2} - \dfrac{{{a^3}}}{{54}} - \dfrac{{{a^3}}}{{16}} = \dfrac{{181{a^3}}}{{432}}\). Chọn D. Câu hỏi 8 : Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy là hình chữ nhật, \(AB = a,\,\,AD = \dfrac{4}{3}a.\) Biết \(A'\) cách đều các đỉnh \(A,\,\,B,\,\,C\) và cạnh bên \(AA' = a.\) Thể tích của khối lăng trụ đã cho bằng:
Đáp án: D Phương pháp giải: - Gọi \(O = AC \cap BD \Rightarrow O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Chứng minh \(A'O \bot \left( {ABCD} \right)\). - Sử dụng định lí Pytago tính \(A'O\). - Tính thể tích \({V_{ABCD.A'B'C'D'}} = A'O.{S_{ABCD}}\). Lời giải chi tiết:
Gọi \(O = AC \cap BD \Rightarrow O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Theo bài ra ta có: Điểm \(A'\) cách đều các đỉnh \(A,\,\,B,\,\,C\) nên \(A'O \bot \left( {ABC} \right)\) hay \(A'O \bot \left( {ABCD} \right)\). \( \Rightarrow A'O \bot AO \Rightarrow \Delta A'AO\) vuông tại \(O\). Áp dụng định lí Pytago ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + \dfrac{{16{a^2}}}{9}} = \dfrac{{5a}}{3}\) \( \Rightarrow AO = \dfrac{1}{2}AC = \dfrac{{5a}}{6}\). \( \Rightarrow A'O = \sqrt {A'{A^2} - A{O^2}} = \sqrt {{a^2} - \dfrac{{25{a^2}}}{{36}}} = \dfrac{{a\sqrt {11} }}{6}\). \({S_{ABCD}} = AB.AD = a.\dfrac{4}{3}a = \dfrac{{4{a^2}}}{3}\). Vậy \({V_{ABCD.A'B'C'D'}} = A'O.{S_{ABCD}} = \dfrac{{a\sqrt {11} }}{6}.\dfrac{{4{a^2}}}{3} = \dfrac{{2\sqrt {11} {a^3}}}{9}\). Chọn D. Câu hỏi 9 : Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\)có \(AB = a,\) đường thẳng \(A'B\) tạo với mặt phẳng \(\left( {BCC'B'} \right)\) một góc \({30^0}.\) Tính thể tích khối lăng trụ \(ABC.A'B'C'.\)
Đáp án: B Phương pháp giải: - Xác định góc giữa \(A'B\) và \(\left( {BCC'B'} \right)\) là góc giữa \(A'B\) và hình chiếu của \(A'B\) lên \(\left( {BCC'B'} \right)\). - Sử dụng công thức tính nhanh: Chiều cao của tam giác đều cạnh \(a\) là \(\dfrac{{a\sqrt 3 }}{2}\) và diện tích tam giác đều cạnh \(a\) là \(\dfrac{{{a^2}\sqrt 3 }}{4}\). - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông và định lí Pytago để tính chiều cao của khối lăng trụ. - Sử dụng công thức tính thể tích khối lăng trụ có chiều cao \(h\), diện tích đáy \(B\) là \(V = B.h\). Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(B'C'\). Vì \(\Delta A'B'C'\) đều nên \(A'M \bot B'C'\). Ta có: \(\left\{ \begin{array}{l}A'M \bot B'C'\\A'M \bot BB'\,\,\left( {BB' \bot \left( {A'B'C'} \right)} \right)\end{array} \right.\) \( \Rightarrow A'M \bot \left( {BCC'B'} \right)\). \( \Rightarrow BM\) là hình chiếu của \(A'M\) lên \(\left( {BCC'B'} \right)\) \( \Rightarrow \angle \left( {A'B;\left( {BCC'B'} \right)} \right) = \angle \left( {A'B;MB} \right) = \angle A'BM = {30^0}\). Theo bài ra ta có \(\Delta A'B'C'\) đều cạnh \(a\) nên \(A'M = \dfrac{{a\sqrt 3 }}{2}\) và \({S_{\Delta A'B'C'}} = \dfrac{{{a^2}\sqrt 3 }}{4}\). Ta có: \(A'M \bot \left( {BCC'B'} \right) \Rightarrow A'M \bot BM\) \( \Rightarrow \Delta A'BM\) vuông tại \(M\) \( \Rightarrow BM = A'M.\cot {30^0} = \dfrac{{3a}}{2}\). Áp dụng định lí Pytago trong tam giác vuông \(BB'M\) ta có: \(BB' = \sqrt {B{M^2} - BB{'^2}} = \sqrt {{{\left( {\dfrac{{3a}}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = a\sqrt 2 \). Vậy \({V_{ABC.A'B'C'}} = BB'.{S_{A'B'C'}} = a\sqrt 2 .\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 6 }}{4}\). Chọn B. Câu hỏi 10 : Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là \(a,\,\,2a,\,\,3a\) có thể tích lớn nhất bằng
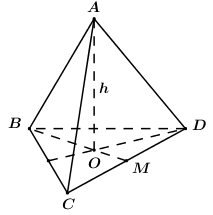
Đáp án: D Phương pháp giải: Khối chóp có thể tích lớn nhất khi 3 cạnh đôi một vuông góc. Lời giải chi tiết:
Giả sử khối chóp \(ABCD\) có \(AB = a,\,\,AC = 2a,\,\,AD = 3a\). Gọi \(H\) là hình chiếu vuông góc của \(D\) lên \(\left( {ABC} \right)\), khi đó ta có: \(DH \bot \left( {ABC} \right)\) và \(DH \le AD\). Ta có: \({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \angle BAC \le \dfrac{1}{2}AB.AC\). Vây \({V_{ABCD}} = \dfrac{1}{3}DH.{S_{\Delta ABC}} \le \dfrac{1}{3}AD.\dfrac{1}{2}AB.AC = \dfrac{1}{6}AB.AC.AD = \dfrac{1}{6}.a.2a.3a = {a^3}\). Dấu “=” xảy ra \( \Leftrightarrow AD \bot \left( {ABC} \right),\,\,AB \bot AC\) hay \(AB,\,\,AC,\,\,AD\) đôi một vuông góc. Chọn D. Câu hỏi 11 : Cho hình chóp S.ABCD có ABCD là hình chữ nhật, \(AB = 2a,\)\(AD = a\)\(\left( {a > 0} \right)\). M là trung điểm của AB, tam giác SMC vuông tại S, \(\left( {SMC} \right) \bot \left( {ABCD} \right),\)\(SM\) tạo với đáy góc \(60^\circ \). Thể tích của khối chóp S.ABCD là:
Đáp án: A Phương pháp giải: - Trong \(\left( {SMC} \right)\) kẻ \(SI \bot MC\,\,\left( {I \in MC} \right)\), chứng minh \(SI \bot \left( {ABCD} \right)\). - Xác định góc giữa \(SM\) và mặt đáy là góc giữa \(SM\) và hình chiếu của \(SM\) lên mặt đáy. - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính chiều cao \(SI\). - Tính thể tích khối chóp \({V_{S.ABCD}} = \dfrac{1}{3}SI.{S_{ABCD}}\). Lời giải chi tiết:
Trong \(\left( {SMC} \right)\) kẻ \(SI \bot MC\,\,\left( {I \in MC} \right)\) ta có: \(\left\{ \begin{array}{l}\left( {SMC} \right) \bot \left( {ABCD} \right) = MC\\SI \subset \left( {SMC} \right),\,\,SI \bot MC\end{array} \right. \Rightarrow SI \bot \left( {ABCD} \right)\). \( \Rightarrow IM\) là hình chiếu của \(SM\) lên \(\left( {ABCD} \right)\). \( \Rightarrow \angle \left( {SM;\left( {ABCD} \right)} \right) = \angle \left( {SM;IM} \right) = \angle SMI = \angle SMC = {60^0}\). Áp dụng định lí Pytago trong tam giác BMC vuông tại B : \(BM = \dfrac{{AB}}{2} = a;\,\,BC = a\)\( \Rightarrow MC = \sqrt {B{C^2} + B{M^2}} = a\sqrt 2 \). Xét tam giác SMC vuông tại \(S\) có \(\angle SMC = {60^0};\,\,MC = a\sqrt 2 \) \( \Rightarrow SM = MC.\cos {60^0} = \dfrac{{a\sqrt 2 }}{2}\). Xét tam giác SMI vuông tại \(I\) có \(\angle SMI = {60^0};\,\,SM = \dfrac{{a\sqrt 2 }}{2}\) \( \Rightarrow SI = SM.sin{60^0} = \dfrac{{a\sqrt 2 }}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 6 }}{4}\). Vậy thể tích khối chóp là \(V = \dfrac{1}{3}SI.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{4}.2{a^2} = \dfrac{{{a^3}\sqrt 6 }}{6}.\) Chọn A. Câu hỏi 12 : Cho khối chóp S.ABC có các góc phẳng ở đỉnh S bằng \(60^\circ ,SA = 1,SB = 2,SC = 3\). Thể tích của khối chóp S.ABC bằng
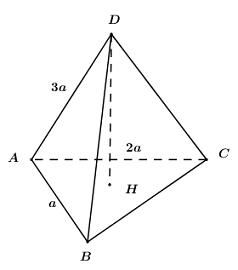
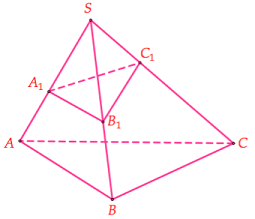
Đáp án: C Phương pháp giải: Áp dụng tỉ số thể tích. Lời giải chi tiết: Ta lấy lần lượt trên cạnh SB; SC các điểm M;N sao cho \(SA = SM = SN = 1\) Khi đó \(\frac{{{V_{SAMN}}}}{{{V_{SABC}}}} = \frac{{SM}}{{SB}}.\frac{{SN}}{{AC}} = \frac{1}{2}.\frac{1}{3} = \frac{1}{6}\) Tứ diện SAMN có góc ở đỉnh S là \(60^\circ \) và các cạnh bên bằng 1\( \Rightarrow SAMN\) là tứ diện đều. Áp dụng công thức tính thể tích tứ diện đều là \(V = \frac{{\sqrt 2 }}{{12}}{a^3} = \frac{{\sqrt 2 }}{{12}}\) Khi đó \({V_{SABC}} = \frac{{\sqrt 2 }}{2}\). Chọn C. Câu hỏi 13 : Cho hình chóp S.ABC có \(SA = SB = SC = a,AB = AC = 2a,BC = 3a\).Thể tích khối chóp S.ABC bằng:
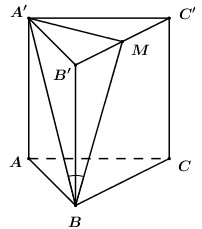
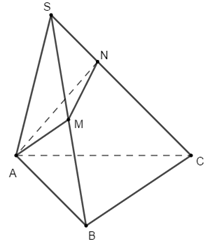
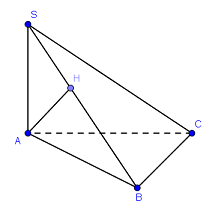
Đáp án: D Phương pháp giải: - Tìm bán kính đường tròn ngoại tiếp tam giác ABC. - Tính chiều cao của hình chóp. - Áp dụng công thức tính thể tích khối chóp. Lời giải chi tiết: Gọi bán kính đường tròn ngoại tiếp tam giác là R. Ta có \(\frac{a}{{\sin A}} = 2R \Rightarrow 2R = \frac{{BC}}{{\sin BAC}}\) Tam giác ABC có \(AB = AC = 2a;BC = 3a\) \( \Rightarrow \cos BAC = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} = - \frac{1}{8} \Rightarrow \sin BAC = \frac{{3\sqrt 7 }}{8}\) \( \Rightarrow {S_{ABC}} = \frac{1}{2}AB.AC.\sin BAC = \frac{{{a^2}.3\sqrt 7 }}{4}\) Khi đó \(R = \frac{{BC}}{{2\sin BAC}} = \frac{{3a}}{{2.\frac{{3\sqrt 7 }}{8}}} = \frac{{4\sqrt 7 }}{7}\) Chiều cao hình chóp là \(h = \sqrt {S{A^2} - {R^2}} = \frac{{\sqrt {35} }}{7}\) Khi đó thể tích hình chóp là \(V = \frac{1}{3}h.{S_{ABC}} = \frac{1}{3}.\frac{{a\sqrt {35} }}{7}.\frac{{3\sqrt 7 }}{4}{a^2} = \frac{{{a^3}\sqrt 5 }}{4}\). Chọn D. Câu hỏi 14 : Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, \(AB = 4,SA = SB = SC = 12\). Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho \(\dfrac{{BF}}{{BS}} = \dfrac{2}{3}\). Thể tích khối tứ diện \(MNEF\) bằng
Đáp án: D Phương pháp giải: Sử dụng công thức tính tỉ số thể tích hai khối chóp tam giác: \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\) Công thức tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao. Lời giải chi tiết:
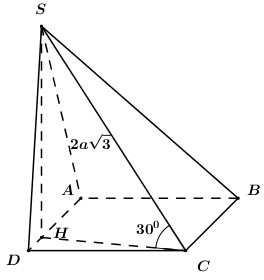
Gọi D là giao điểm của MB và EN thì D là trung điểm của MB. Ta có: \({V_{MNEF}} = {V_{M.NEF}} = \dfrac{1}{3}{S_{NEF}}.d\left( {M,\left( {NEF} \right)} \right)\) Do D là trung điểm của MB và MB cắt (EFN) tại D nên \(d\left( {M,\left( {NEF} \right)} \right) = d\left( {B,\left( {NEF} \right)} \right)\) \( \Rightarrow {V_{MNEF}} = \dfrac{1}{3}{S_{NEF}}.d\left( {B,\left( {NEF} \right)} \right)\)\( = {V_{B.NEF}}\) Mà \(\dfrac{{{V_{B.NEF}}}}{{{V_{B.CAS}}}} = \dfrac{{BN}}{{BC}}.\dfrac{{BE}}{{BA}}.\dfrac{{BF}}{{BS}}\)\( = \dfrac{1}{2}.\dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{6}\) \( \Rightarrow {V_{B.NEF}} = \dfrac{1}{6}{V_{B.CAS}} = \dfrac{1}{6}{V_{S.ABC}}\) Vì SA=SB=SC nên \(S\) nằm trên trục đường tròn ngoại tiếp tam giác ABC. Mà ABC vuông cân nên M là tâm đường tròn ngoại tiếp tam giác. Do đó \(SM \bot \left( {ABC} \right)\). Diện tích tam giác \(ABC\) là \({S_{ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}.4.4 = 8\) Tam giác ABC vuông cân tại B nên \(\begin{array}{l}AC = \sqrt {A{B^2} + B{C^2}} \\ = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \\ \Rightarrow AM = \dfrac{1}{2}AC = \dfrac{1}{2}.4\sqrt 2 = 2\sqrt 2 \end{array}\) Tam giác \(SMA\) vuông tại M nên theo Pitago ta có: \(SM = \sqrt {S{A^2} - A{M^2}} \)\( = \sqrt {{{12}^2} - {{\left( {2\sqrt 2 } \right)}^2}} = 2\sqrt {34} \) Thể tích khối chóp S.ABC là: \({V_{S.ABC}} = \dfrac{1}{3}{S_{ABC}}.SM\)\( = \dfrac{1}{2}.8.2\sqrt {34} = 8\sqrt {34} \) Thể tích khối tứ diện MNEF là: \({V_{MNEF}} = \dfrac{1}{6}.{V_{S.ABC}}\)\( = \dfrac{1}{6}.8\sqrt {34} = \dfrac{{4\sqrt {34} }}{3}\) Chọn D. Câu hỏi 15 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, mặt bên \(SAD\) là tam giác vuông tại \(S\). Hình chiếu vuông góc của \(S\) trên mặt đáy là điểm \(H\) thuộc cạnh \(AD\) sao cho \(HA = 3HD\). Biết rằng \(SA = 2a\sqrt 3 \) và \(SC\) tạo với đáy một góc bằng \({30^0}\). Tính theo \(a\) thể tích \(V\) của khối chóp \(S.ABCD\).
Đáp án: D Phương pháp giải: - Đặt \(AD = 4x \Rightarrow AH = 3x,\,\,HD = x\). Áp dụng hệ thức lượng trong tam giác vuông \(S{A^2} = AH.HD\) biểu diễn \(x\) theo \(a\). - Tính chiều cao \(SH\), sử dụng hệ thức lượng trong tam giác vuông \(S{H^2} = AH.HD\) . - Xác định góc giữa \(SC\) và \(\left( {ABCD} \right)\) là góc giữa \(SC\) và hình chiếu của \(SC\) lên \(\left( {ABCD} \right)\), từ đó tính độ dài \(HC\). - Áp dụng định lí pytago trong tam giác vuông tính \(CD\) và tính \({S_{ABCD}}\). - Sử dụng công thức tính thể tích khối chóp \(V = \dfrac{1}{3}SH.{S_{ABCD}}\). Lời giải chi tiết:
Đặt \(AD = 4x \Rightarrow AH = 3x,\,\,HD = x\). Áp dụng hệ thức lượng trong tam giác vuông \(SAD\) có: \(\begin{array}{l}S{A^2} = AH.AD\\ \Leftrightarrow 12{a^2} = 3x.4x = 12{x^2}\\ \Leftrightarrow x = a\end{array}\) \( \Rightarrow AD = 4a,\,\,AH = 3a,\,\,HD = a\). Lại có: \(S{H^2} = AH.HD = 3a.a = 3{a^2}\) \( \Rightarrow SH = a\sqrt 3 \). Ta có \(SH \bot \left( {ABCD} \right)\) nên \(HC\) là hình chiếu vuông góc của \(SC\) lên \(\left( {ABCD} \right)\). \( \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;HC} \right) = \angle SCH = {30^0}\). Xét tam giác vuông \(SHC\) có: \(HC = SH.cot{30^0} = a\sqrt 3 .\sqrt 3 = 3a\). Áp dụng định lí Pytago trong tam giác vuông \(CDH\) có: \(CD = \sqrt {C{H^2} - H{D^2}} = \sqrt {9{a^2} - {a^2}} = 2a\sqrt 2 \). \( \Rightarrow {S_{ABCD}} = AD.CD = 4a.2a\sqrt 2 = 8\sqrt 2 {a^2}\). Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{1}{3}.a\sqrt 3 .8\sqrt 2 {a^2} = \dfrac{{8{a^3}\sqrt 6 }}{3}\). Chọn D. Câu hỏi 16 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\). Tam giác \(ABC\) đều, hình chiếu vuông góc \(H\) của đỉnh \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) trùng với trọng tâm của tam giác \(ABC\). Đường thẳng \(SD\) hợp với mặt phẳng \(\left( {ABCD} \right)\) góc \({30^0}\). Tính theo \(a\) thể tích \(V\) của khối chóp \(S.ABCD\).
Đáp án: C Phương pháp giải: - Gọi \(O = AC \cap BD\), \(H\) là trọng tâm \(\Delta ABC\) \( \Rightarrow SH \bot \left( {ABCD} \right)\). - Dựa vào tam giác \(ABC\) đều cạnh \(a\), tính độ dài các đoạn thẳng \(BH,\,\,HD\). - Xác định góc giữa \(SD\) và \(\left( {ABCD} \right)\) là góc giữa \(SD\) và hình chiếu của \(SD\) lên \(\left( {ABCD} \right)\). - Dựa vào tỉ số lượng giác của góc nhọn trong tam giác vuông tính độ dài đường cao \(AH\). - Tính \({S_{\Delta ABC}}\), từ đó suy ra \({S_{ABCD}} = 2{S_{\Delta ABC}}\). - Sử dụng công thức tính thể tích \(V = \dfrac{1}{3}SH.{S_{ABCD}}\). Lời giải chi tiết:
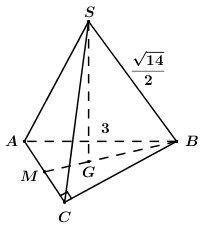
Gọi \(O = AC \cap BD\), \(H\) là trọng tâm \(\Delta ABC\) \( \Rightarrow SH \bot \left( {ABCD} \right)\). Tam giác \(ABC\) đều cạnh \(a\) \( \Rightarrow BO = \dfrac{{a\sqrt 3 }}{2} \Rightarrow BD = a\sqrt 3 \) và \({S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\) \( \Rightarrow {S_{ABCD}} = 2{S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{2}\). \(H\) là trọng tâm \(\Delta ABC\) \( \Rightarrow BH = \dfrac{2}{3}BO = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\) \( \Rightarrow HD = BD - BH = a\sqrt 3 - \dfrac{{a\sqrt 3 }}{3} = \dfrac{{2a\sqrt 3 }}{3}\). Vì \(SH \bot \left( {ABCD} \right)\) nên \(HD\) là hình chiếu của \(SD\) lên \(\left( {ABCD} \right)\) \( \Rightarrow \angle \left( {SD;\left( {ABCD} \right)} \right) = \angle \left( {SD;HD} \right) = \angle SDH = {30^0}\). Xét tam giác vuông \(SHD\) có: \(SH = HD.\tan {30^0} = \dfrac{{2a\sqrt 3 }}{3}.\dfrac{1}{{\sqrt 3 }} = \dfrac{{2a}}{3}\). Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{2a}}{3}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{9}\). Chọn C. Câu hỏi 17 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(C\), cạnh huyền \(AB\) bằng 3. Hình chiếu vuông góc của \(S\) xuống mặt đáy trùng với của tam giác \(ABC\) và \(SB = \dfrac{{\sqrt {14} }}{2}\). Tính theo \(a\) thể tích \(V\) của khối chóp \(S.ABC\)?
Đáp án: C Phương pháp giải: - Tính độ dài các cạnh \(AC,\,\,BC\). - Gọi \(G\) là trọng tâm \(\Delta ABC\) và \(M\) là trung điểm của \(AC\), áp dụng định lí Pytago tính \(BM\), từ đó suy ra độ dài \(BG\). - Tiếp tục áp dụng định lí Pytago tính độ dài đường cao \(SG\). - Sử dụng công thức tính thể tích khối chóp \({V_{S.ABC}} = \dfrac{1}{3}SG.{S_{\Delta ABC}}\). Lời giải chi tiết:
Do tam giác \(ABC\) vuông cân tại \(C\) có \(AB = 3\) nên \(AC = BC = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{3}{{\sqrt 2 }}\). Gọi \(G\) là trọng tâm \(\Delta ABC\) và \(M\) là trung điểm của \(AC\), khi đó ta có \(SG \bot \left( {ABC} \right)\) và \(AM = MC = \dfrac{1}{2}AC = \dfrac{3}{{2\sqrt 2 }}\). Áp dụng định lí Pytago trong tam giác vuông \(BCM\) có: \(BM = \sqrt {B{C^2} + C{M^2}} = \sqrt {\dfrac{9}{2} + \dfrac{9}{8}} = \sqrt {\dfrac{{45}}{8}} = \dfrac{{3\sqrt {10} }}{4}\). \( \Rightarrow GB = \dfrac{2}{3}BM = \dfrac{2}{3}.\dfrac{{3\sqrt {10} }}{4} = \dfrac{{\sqrt {10} }}{2}\). Áp dụng định lý Pytago trong tam giác vuông \(SBG\) có: \(SG = \sqrt {S{B^2} - B{G^2}} = \sqrt {\dfrac{{14}}{4} - \dfrac{{10}}{4}} = 1\). Lại có: \({S_{\Delta ABC}} = \dfrac{1}{2}AC.BC = \dfrac{1}{2}.\dfrac{3}{{\sqrt 2 }}.\dfrac{3}{{\sqrt 2 }} = \dfrac{9}{4}\). Vậy \({V_{S.ABC}} = \dfrac{1}{3}SG.{S_{\Delta ABC}} = \dfrac{1}{3}.1.\dfrac{9}{4} = \dfrac{3}{4}\). Chọn C. Câu hỏi 18 : Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác đều. Mặt phẳng \(\left( {{A_1}BC} \right)\) tạo với đáy góc \({30^0}\) và tam giác \({A_1}BC\) có diện tích bằng 8. Tính thể tích V của khối lăng trụ đã cho.
Đáp án: D Phương pháp giải: - Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến. - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính chiều cao của khối lăng trụ. - Sử dụng công thức tính thể tích khối lăng trụ có chiều cao \(h\), diện tích đáy \(B\) là \(V = Bh\). Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(BC\). Do tam giác \(ABC\) đều nên \(AM \bot BC\). Ta có: \(\left\{ \begin{array}{l}BC \bot AM\\BC \bot AA'\end{array} \right. \Rightarrow BC \bot \left( {AA'M} \right) \Rightarrow BC \bot A'M\). \(\left\{ \begin{array}{l}\left( {A'BC} \right) \cap \left( {ABC} \right) = BC\\AM \subset \left( {ABC} \right),\,AM \bot BC\\A'M \subset \left( {A'BC} \right),A'M \bot BC\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {A'BC} \right);\left( {ABC} \right)} \right) = \angle AMA' = {30^0}\). Giả sử tam giác \(ABC\) đều, cạnh a \( \Rightarrow AM = \dfrac{{a\sqrt 3 }}{2},\,BC = a\). Tam giác \(AMA'\) vuông tại \(A\)\( \Rightarrow A'M = \dfrac{{AM}}{{\cos \angle AMA'}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{{\cos {{30}^0}}} = a\). Ta có: \({S_{\Delta A'BC}} = \dfrac{1}{2}A'M.BC = 8 \Leftrightarrow \dfrac{1}{2}.a.a = 8 \Leftrightarrow {a^2} = 16 \Leftrightarrow a = 4\). Khi đó ta có: \(AA' = AM.\tan {30^0} = \dfrac{{a\sqrt 3 }}{2}.\dfrac{1}{{\sqrt 3 }} = \dfrac{a}{2} = \dfrac{4}{2} = 2\). Tam giác \(ABC\) đều cạnh \(4\) \( \Rightarrow {S_{\Delta ABC}} = \dfrac{{{4^2}\sqrt 3 }}{4} = 4\sqrt 3 \). Vậy thể tíchcủa khối lăng trụ đã cho là: \(V = AA'.{S_{\Delta ABC}} = 2.4\sqrt 3 = 8\sqrt 3 \). Chọn D. Câu hỏi 19 : Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh đều bằng a, tâm của đáy là O. Gọi M, N tương ứng là trung điểm của các cạnh SA, SC. Gọi E là giao điểm của SD và mặt phẳng (BMN). Tính thể tích V của khối chóp O.BMEN.
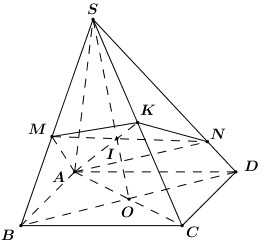
Đáp án: A Phương pháp giải: +) Định lí Menelaus: Cho tam giác ABC. Các điểm D, E, F lần lượt nằm trên các đường thẳng BC, CA, AB. Khi đó D, E, F thẳng hàng khi và chỉ khi \(\dfrac{{FA}}{{FB}}.\dfrac{{DB}}{{DC}}.\dfrac{{EC}}{{EA}} = 1\){\displaystyle {\frac {\overline {FA}}{\overline {FB}}}\cdot {\frac {\overline {DB}}{\overline {DC}}}\cdot {\frac {\overline {EC}}{\overline {EA}}}=1.} +) Thể tích hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh đều bằng a là: \(V = \dfrac{{{a^3}\sqrt 2 }}{6}\) Lời giải chi tiết:
Gọi I là giao điểm của SO và MN. Khi đó, giao điểm E của SD và mặt phẳng (BMN) là giao của ID và SB. Xét tam giác SOD, có: \(\dfrac{{ES}}{{ED}}.\dfrac{{BD}}{{BO}}.\dfrac{{IO}}{{IS}} = 1 \Leftrightarrow \dfrac{{ES}}{{ED}}.2.1 = 1 \Leftrightarrow \dfrac{{ES}}{{ED}} = \dfrac{1}{2}\)\( \Rightarrow \dfrac{{SE}}{{SD}} = \dfrac{1}{3}\) Do I là trung điểm của SO nên \(d\left( {O;\left( {BNEM} \right)} \right) = d\left( {S;\left( {BNEM} \right)} \right)\)\( \Rightarrow {V_{O.BNEM}} = {V_{S.BNEM}}\) Lại có: \({V_{S.ENB}} = \dfrac{{SN}}{{SC}}.\dfrac{{SE}}{{SD}}.{V_{S.BDC}} = \dfrac{1}{2}.\dfrac{1}{3}.{V_{S.BDC}} = \dfrac{1}{6}{V_{S.BDC}} = \dfrac{1}{{12}}{V_{S.ABCD}}\) và \({V_{S.EMB}} = \dfrac{1}{{12}}{V_{S.ABCD}}\) \( \Rightarrow {V_{S.BNEM}} = \dfrac{1}{6}{V_{S.ABCD}} = \dfrac{1}{6}.\dfrac{{{a^3}\sqrt 2 }}{6} = \dfrac{{{a^3}\sqrt 2 }}{{36}}\). Chọn A. Câu hỏi 20 : Cho hình chóp \(S.ABC\) có đáy \(ABCD\) là hình thoi \(AB = a,\,\widehat {ABC} = {60^0}\). \(SA \bot \left( {ABCD} \right)\) và SC tạo với mặt phẳng \(\left( {SAB} \right)\) một góc \({45^0}\). Tính thể tích \(V\) của khối chóp \(S.ABC\).
Đáp án: C Phương pháp giải: - Chứng minh \(\Delta ABC\) đều, sử dụng công thức tính nhanh diện tích tam giác đều cạnh a là \(S = \dfrac{{{a^2}\sqrt 3 }}{4}\). - Xác định góc giữa SC và (SAB) là góc giữa SC và hình chiếu của SC lên (SAB). - Sử dụng tỉ số lượng giác và định lí Pytago tính độ dài SA. - Sử dụng công thức tính thể tích \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}}\). Lời giải chi tiết:
Tam giác ABC có AB = BC, \(\,\angle ABC = {60^0}\) \( \Rightarrow \Delta ABC\) đều, có cạnh \(AB = a\)\( \Rightarrow {S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\). Gọi I là trung điểm của AB \( \Rightarrow CI \bot AB\) (do tam giác ABC đều). Mà \(CI \bot SA \Rightarrow CI \bot \left( {SAB} \right)\)\( \Rightarrow \) Hình chiếu của SC lên (SAB) là SI. \( \Rightarrow \angle \left( {SC;\left( {SAB} \right)} \right) = \angle \left( {SC;SI} \right) = \angle ISC = {45^0}\) \( \Rightarrow \Delta SIC\) vuông cân tại I \( \Rightarrow SI = IC = \dfrac{{a\sqrt 3 }}{2}\). Ta có: \(\Delta SAI\) vuông tại A \( \Rightarrow SA = \sqrt {S{I^2} - A{I^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt 2 }}{2}\) Vậy thể tích khối chóp \(S.ABC\) là: \(V = \dfrac{1}{3}.SA.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{a\sqrt 2 }}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 6 }}{{24}}\). Chọn C. Câu hỏi 21 : Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Gọi \(M\),\(N\), \(P\), \(Q\), \(R\), \(S\) là tâm các mặt của hình lập phương. Thể tích khối bát diện đều tạo bởi sáu đỉnh \(M\), \(N\), \(P\), \(Q\), \(R\), \(S\) bằng:
Đáp án: B Phương pháp giải: Sử dụng công thức tính thể tích khối chóp có chiều cao \(h\), diện tích đáy \(B\) là \(V = \dfrac{1}{3}Bh\). Lời giải chi tiết:
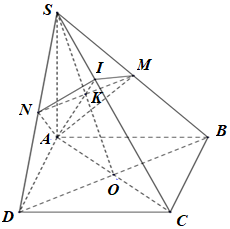
Gọi \(E,\,\,F,\,\,G,\,\,H\) lần lượt là trung điểm của \(BB',\,\,AA',\,\,DD',\,\,CC'\), khi đó ta có \(\left( {EFGH} \right) \equiv \left( {MNPQ} \right)\). Gọi \(O\) là tâm hình lập phương, khi đo \(O\) là trung điểm của \(RS\) và \(RS \bot \left( {MNPQ} \right)\) tại \(O\). Ta có: \(\begin{array}{l}{V_{RSMNPQ}} = {V_{R.MNPQ}} + {V_{S.MNPQ}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}RO.{S_{MNPQ}} + \dfrac{1}{3}SO.{S_{MNPQ}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}RS.{S_{MNPQ}}\end{array}\) Do \(EFGH\) là hình vuông cạnh \(a\) nên \(MN = NP = \dfrac{1}{2}EG = \dfrac{{a\sqrt 2 }}{2}\). \( \Rightarrow {S_{MNPQ}} = MN.NP = \dfrac{{{a^2}}}{2}\), \(RS = a\). Vậy \({V_{RS.MNPQ}} = \dfrac{1}{3}.a.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}}}{6}\). Chọn B. Câu hỏi 22 : Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh AB = 2a, \(\Delta SAB\) là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi M, N lần lượt là trung điểm của AB, BC và G là trọng tâm \(\Delta SCD\). Biết khoảng cách từ điểm M đến mặt phẳng (SND) bằng \(\dfrac{{3a\sqrt 2 }}{4}\). Thể tích khối chóp G.AMND được tính theo a bằng:
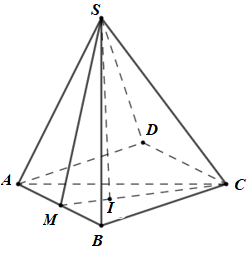
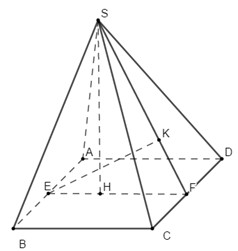
Đáp án: D Phương pháp giải: - Chứng minh \(SM \bot \left( {ABCD} \right)\). - Trong (ABCD) kẻ \(MI \bot ND\,\,\left( {I \in ND} \right)\), trong (SMI) kẻ \(MH \bot SI\). Chứng minh \(MH = d\left( {M;\left( {SND} \right)} \right)\). - Tính \({S_{MND}}\), từ đó tính MI. - Áp dụng hệ thức lượng trong tam giác vuông tính SM, từ đó suy ra \(d\left( {G;\left( {ABCD} \right)} \right)\). - Tính diện tích tứ giác AMND: \({S_{AMND}} = {S_{ABCD}} - {S_{BMN}} - {S_{CND}}\). - Áp dụng công thức tính thể tích: \({V_{G.AMND}} = \dfrac{1}{3}d\left( {G;\left( {ABCD} \right)} \right).{S_{AMND}}\). Lời giải chi tiết:
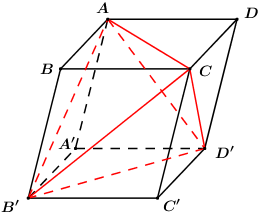
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right) = AB\\SM \subset \left( {SAB} \right),\,\,SM \bot AB\end{array} \right.\)\( \Rightarrow SM \bot \left( {ABCD} \right)\). Trong (ABCD) kẻ \(MI \bot ND\,\,\left( {I \in ND} \right)\), trong (SMI) kẻ \(MH \bot SI\). Ta có: \(\left\{ \begin{array}{l}ND \bot MI\\ND \bot SM\end{array} \right. \Rightarrow ND \bot \left( {SMI} \right) \Rightarrow ND \bot MH\). \(\left\{ \begin{array}{l}MH \bot ND\\MH \bot SI\end{array} \right. \Rightarrow MH \bot \left( {SND} \right)\) \( \Rightarrow d\left( {M;\left( {SND} \right)} \right) = MH = \dfrac{{3a\sqrt 2 }}{4}\). Ta có: \(\begin{array}{l}{S_{BMN}} = \dfrac{1}{2}BM.BN = \dfrac{1}{2}.a.a = \dfrac{{{a^2}}}{2}\\{S_{AMD}} = \dfrac{1}{2}AM.AD = \dfrac{1}{2}.a.2a = {a^2}\\{S_{CND}} = \dfrac{1}{2}CN.CD = \dfrac{1}{2}.a.2a = {a^2}\\{S_{ABCD}} = A{B^2} = 4{a^2}\\ \Rightarrow {S_{MND}} = {S_{ABCD}} - {S_{BMN}} - {S_{AMD}} - {S_{CND}}\\ \Rightarrow {S_{MND}} = 4{a^2} - \dfrac{{{a^2}}}{2} - {a^2} - {a^2} = \dfrac{{3{a^2}}}{2}\end{array}\) Lại có \(ND = \sqrt {C{N^2} + C{D^2}} = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 \), \({S_{MND}} = \dfrac{1}{2}MI.ND\). \( \Rightarrow MI = \dfrac{{2{S_{MND}}}}{{ND}} = \dfrac{{2.\dfrac{{3{a^2}}}{2}}}{{a\sqrt 5 }} = \dfrac{{3a\sqrt 5 }}{5}\). Áp dụng hệ thức lượng trong tam giác vuông SMI có: \(\begin{array}{l}\dfrac{1}{{M{H^2}}} = \dfrac{1}{{S{M^2}}} + \dfrac{1}{{M{N^2}}}\\\dfrac{1}{{{{\left( {\dfrac{{3a\sqrt 2 }}{4}} \right)}^2}}} = \dfrac{1}{{S{M^2}}} + \dfrac{1}{{{{\left( {\dfrac{{3a\sqrt 5 }}{5}} \right)}^2}}}\\ \Rightarrow \dfrac{1}{{S{M^2}}} = \dfrac{1}{{3{a^2}}} \Rightarrow SM = a\sqrt 3 \end{array}\) Gọi P là trung điểm của CD, ta có \(SG \cap \left( {ABCD} \right) = P\) \( \Rightarrow \dfrac{{d\left( {G;\left( {ABCD} \right)} \right)}}{{d\left( {S;\left( {ABCD} \right)} \right)}} = \dfrac{{GP}}{{SP}} = \dfrac{1}{3}\) \( \Rightarrow d\left( {G;\left( {ABCD} \right)} \right) = \dfrac{1}{3}SM = \dfrac{{a\sqrt 3 }}{3}\). \(\begin{array}{l}{S_{AMND}} = {S_{ABCD}} - {S_{BMN}} - {S_{CND}}\\{S_{AMND}} = 4{a^2} - \dfrac{1}{2}{a^2} - {a^2} = \dfrac{{5{a^2}}}{2}\end{array}\) Vậy \({V_{G.AMND}} = \dfrac{1}{3}d\left( {G;\left( {ABCD} \right)} \right).{S_{AMND}}\) \( = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{3}.\dfrac{{5{a^2}}}{2} = \dfrac{{5\sqrt 3 {a^3}}}{{18}}\). Chọn D. Câu hỏi 23 : Cho hình hộp ABCD.A’B’C’D’. Tỉ số thể tích của khối tứ diện ACB’D’ và thể tích khối hộp ABCD.A’B’C’D’ bằng:
Đáp án: D Phương pháp giải: - Phân chia và lắp ghép các khối đa diện. - Muốn so sánh thể tích hai khối hình ta so sánh tỉ số chiều cao và tỉ số diện tích đáy của hai khối hình đó. Lời giải chi tiết:
Đặt \({V_{ABCD.A'B'C'D'}} = V\). Ta có: \({V_{ABCD.A'B'C'D'}} = {V_{ACB'D'}} + {V_{B'.ABC}} + {V_{D'.ACD}} + {V_{A.A'B'D'}} + {V_{C.B'C'D'}}\). Ta có: \({V_{B'.ABC}} = \dfrac{1}{3}d\left( {B';\left( {ABC} \right)} \right).{S_{\Delta ABC}}\)\( = \dfrac{1}{3}d\left( {B';\left( {ABCD} \right)} \right).\dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{6}V\). Chứng minh tương tự ta có: \({V_{D'.ACD}} = {V_{A.A'B'D'}} = {V_{C.B'C'D'}} = \dfrac{1}{6}V\). Khi đó ta có: \(V = {V_{ACB'D'}} + 4.\dfrac{1}{6}V \Leftrightarrow {V_{ACB'D'}} = \dfrac{V}{3}\). Vậy \(\dfrac{{{V_{ACB'D'}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{V}{3}:V = \dfrac{1}{3}.\) Chọn D. Câu hỏi 24 : Cho tứ diện đều có chiều cao bằng h. Thể tích của khối tứ diện đã cho là:
Đáp án: B Phương pháp giải: - Gọi tứ diện đều ABCD cạnh a, sử dụng tính chất tam giác đều và định lí Pytago tính a theo h. - Sử dụng công thức tính thể tích khối chóp có đường cao h, diện tích đáy B là \(V = \dfrac{1}{3}Bh\). Lời giải chi tiết:
Gọi tứ diện đều ABCD cạnh a, O là trọng tâm tam giác dều BCD \( \Rightarrow AO \bot \left( {BCD} \right)\). Gọi M là trung điểm của CD. Tam giác BCD đều cạnh a \( \Rightarrow BM = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow BO = \dfrac{2}{3}BM = \dfrac{{a\sqrt 3 }}{3}\). Áp dụng định lí Pytago trong tam giác vuông ABO ta có: \(\begin{array}{l}A{B^2} = B{O^2} + A{O^2}\\ \Leftrightarrow {a^2} = \dfrac{{{a^2}}}{3} + {h^2}\\ \Leftrightarrow \dfrac{{2{a^2}}}{3} = {h^2}\\ \Leftrightarrow {a^2} = \dfrac{{3{h^2}}}{2}\end{array}\) \( \Rightarrow {S_{\Delta BCD}} = \dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{h^2}}}{2}.\dfrac{{\sqrt 3 }}{4} = \dfrac{{3\sqrt 3 {h^2}}}{8}\). Vậy \({V_{ABCD}} = \dfrac{1}{3}AO.{S_{\Delta BCD}} = \dfrac{1}{3}.h.\dfrac{{3\sqrt 3 {h^2}}}{8} = \dfrac{{\sqrt 3 {h^3}}}{8}.\) Chọn B. Câu hỏi 25 : Cho hình chóp đều \(S.ABCD\) có độ dài cạnh đáy bằng \(2a\). Gọi \(G\) là trọng tâm tam giác \(SAC\). Mặt phẳng chứa \(AB\) và đi qua \(G\) cắt các cạnh \(SC\), \(SD\) lần lượt tại \(M\) và \(N\). Biết mặt bên của hình chóp tạo với đáy một góc bằng \(60^\circ \). Thể tích khối chóp \(S.ABMN\) bằng:
Đáp án: A Phương pháp giải: - Xác định các điểm \(M,\,\,N\), chứng minh \(M,\,\,N\) lần lượt là trung điểm của \(SC,\,\,SD\). - Xác định góc giữa mặt bên và mặt đáy là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến. - Tính đường cao \(SO\) với \(O\) là tâm hình vuông \(ABCD\), từ đó tính \({V_{S.ABCD}}\). - Tách \({V_{S.ABMN}} = {V_{S.ABM}} + {V_{S.AMN}}\). - Sử dụng tỉ lệ thể tích Simpson. Lời giải chi tiết:
Vì \(G\) là trọng tâm tam giác \(SAC\) nên \(AG\) cắt \(SC\) tại trung điểm \(M\) của \(SC\), tương tự \(BG\) cắt \(SD\) tại trung điểm \(N\) của \(SD\). Gọi \(O\) là tâm của hình vuông \(ABCD\) và \(I\) là trung điểm của \(AB\). Ta có: \(\left\{ \begin{array}{l}AB \bot OI\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOI} \right) \Rightarrow AB \bot SI\). \(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SAB} \right) \supset SI \bot AB\\\left( {ABCD} \right) \supset OI \bot AB\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {SAB} \right);\left( {ABCD} \right)} \right) = \angle \left( {SI;OI} \right) = \angle SIO = {60^0}\). Xét tam giác vuông \(SOI\) có: \(SO = OI.\tan 60^\circ = a\sqrt 3 \). Suy ra \({V_{S.ABCD}} = \dfrac{1}{3}{S_{ABCD}}.SO = \dfrac{1}{3}4{a^2} \cdot a\sqrt 3 = \dfrac{{4{a^3}\sqrt 3 }}{3}\). Ta có: \(\dfrac{{{V_{S.ABM}}}}{{{V_{S.ABC}}}} = \dfrac{{SA}}{{SA}} \cdot \dfrac{{SB}}{{SB}} \cdot \dfrac{{SM}}{{SC}} = \dfrac{1}{2}\) \( \Rightarrow {V_{S.ABM}} = \dfrac{1}{2}.{V_{S.ABC}} = \dfrac{1}{4}{V_{S.ABCD}}\). \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ACD}}}} = \dfrac{{SA}}{{SA}} \cdot \dfrac{{SN}}{{SD}} \cdot \dfrac{{SM}}{{SC}} = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4}\) \( \Rightarrow {V_{S.AMN}} = \dfrac{1}{4}.{V_{S.ACD}} = \dfrac{1}{8}{V_{S.ABCD}}\). Vậy \({V_{S.ABMN}} = {V_{S.ABM}} + {V_{S.AMN}} = \dfrac{3}{8}{V_{S.ABCD}}\)\( = \dfrac{3}{8}\dfrac{{4{a^3}\sqrt 3 }}{3} = \dfrac{{{a^3}\sqrt 3 }}{2}\). Chọn A. Câu hỏi 26 : Cho hình lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(a\). Hình chiếu vuông góc của điểm \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trọng tâm tam giác \(ABC\). Biết khoảng cách giữa hai đường thẳng \(AA'\) và \(BC\) bằng \(\dfrac{{a\sqrt 3 }}{4}\). Tính theo \(a\) thể tích \(V\) của khối lăng trụ \(ABC.A'B'C'\).
Đáp án: B Phương pháp giải: - Xác định đoạn vuông góc chung của hai đoạn thẳng \(AA'\) và \(BC\). - Áp dụng hệ thức lượng trong tam giác vuông tính \(A'G\). - Áp dụng công thức tính thể tích \({V_{ABC.A'B'C'}} = A'G.{S_{ABC}}\). Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(BC\). Vì tam giác \(ABC\) đều nên \(AM \bot BC\) và \(AM = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow AG = \dfrac{2}{3}AM = \dfrac{{a\sqrt 3 }}{3}\). Ta có \(A'G \bot \left( {ABC} \right)\) nên \(A'G \bot BC\); \(BC \bot AM\) \( \Rightarrow BC \bot \left( {MAA'} \right)\). Trong \(\left( {AA'M} \right)\) kẻ \(MI \bot AA'\) tại \(I\); khi đó ta có \(BC \bot IM\) nên \(IM\) là đoạn vuông góc chung của \(AA'\) và \(BC\), do đó \(d\left( {AA';{\rm{ }}BC} \right) = IM = \dfrac{{a\sqrt 3 }}{4}.\) Trong \(\left( {AA'M} \right)\) kẻ \(GH \bot AA'\) tại \(H\), áp dụng định lí Ta-lét ta có \(\dfrac{{AG}}{{AM}} = \dfrac{{GH}}{{IM}} = \dfrac{2}{3}\)\( \Leftrightarrow GH = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{4} = \dfrac{{a\sqrt 3 }}{6}\). Áp dụng hệ thức lượng trong tam giác vuông \(AA'G\) ta có: \(\dfrac{1}{{H{G^2}}} = \dfrac{1}{{A'{G^2}}} + \dfrac{1}{{A{G^2}}} \Leftrightarrow A'G = \dfrac{{AG.HG}}{{\sqrt {A{G^2} - H{G^2}} }} = \dfrac{{\dfrac{{a\sqrt 3 }}{3}.\dfrac{{a\sqrt 3 }}{6}}}{{\sqrt {\dfrac{{{a^2}}}{3} - \dfrac{{{a^2}}}{{12}}} }} = \dfrac{a}{3}\). Tam giác \(ABC\) đều cạnh \(a\) nên \({S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\). Vậy \({V_{ABC.A'B'C'}} = A'G.{S_{ABC}} = \dfrac{a}{3}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{{12}}\). Chọn B. Câu hỏi 27 : Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(C\), biết \(AB = 2a\), \(AC = a\), \(BC' = 2a\). Tính thể tích \(V\) của khối lăng trụ đã cho.
Đáp án: C Phương pháp giải: - Áp dụng định lí Pytago để tính các cạnh còn lại của tam giác đáy, tính ch iều cao của lăng trụ. - Thể tích khối lăng trụ có chiều cao \(h\), diện tích đáy \(B\) là: \(V = B.h\). Lời giải chi tiết:
Tam giác \(ABC\) vuông tại \(C\) nên áp dụng định lí Pytago ta có: \(BC = \sqrt {A{B^2} - A{C^2}} = a\sqrt 3 \). \( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AC.BC = \dfrac{1}{2}.a.a\sqrt 3 = \dfrac{{{a^2}\sqrt 3 }}{2}\). Ta có: \(CC' \bot \left( {ABC} \right)\) nên \(CC' \bot BC\), suy ra tam giác \(BCC'\) vuông tại \(C\). Áp dụng định lí Pytago ta có: \(CC' = \sqrt {BC{'^2} - B{C^2}} = a\). Vậy \({V_{ABC.A'B'C'}} = CC'.{S_{\Delta ABC}} = a.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{2}\). Chọn C. Câu hỏi 28 : Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại C, \(AB = 2a\) và góc tạo bởi hai mặt phẳng \(\left( {ABC'} \right)\) và \(\left( {ABC} \right)\) bằng \({60^0}\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(A'C',\,\,BC\). Mặt phẳng \(\left( {AMN} \right)\) chia khối lăng trụ thành hai phần. Thể tích của phần nhỏ hơn bằng :
Đáp án: A Phương pháp giải: - Xác định thiết diện của hình lăng trụ cắt bởi mặt phẳng \(\left( {AMN} \right)\). - Công thức thể tích khối chóp cụt: \(V = \dfrac{1}{3}\left( {B + B' + \sqrt {BB'} } \right)h\) trong đó \(B,\,\,B'\) lần lượt là diện tích hai đáy, \(h\) là chiều cao của khối chóp cụt. Lời giải chi tiết:
Gọi \(ME = \left( {AMN} \right) \cap \left( {A'B'C'} \right)\) , ta có:\(\left\{ \begin{array}{l}\left( {ABC} \right)//\left( {A'B'C'} \right)\\\left( {ANM} \right) \cap \left( {ABC} \right) = AN\\\left( {ANM} \right) \cap \left( {A'B'C'} \right) = ME\end{array} \right.\,\, \Rightarrow AN\parallel ME.\) Khi đó thiết diện của lăng trụ cắt bởi \(\left( {AMN} \right)\) là tứ giác \(AMEN\). Đặt \({V_1} = {V_{ANC.MEC'}},\,\,{V_2} = {V_{ABN.A'B'EM}}\) với \(ANC.MEC'\) là hình chóp cụt. Gọi \(F\) là trung điểm của \(AB\) \( \Rightarrow CF \bot AB\) (trung tuyến đồng thời là đường cao). Mà \(CC' \bot AB \Rightarrow AB \bot \left( {CFC'} \right) \Rightarrow AB \bot C'F.\) Ta có: \(\left\{ \begin{array}{l}\left( {ABC'} \right) \cap \left( {ABC} \right) = AB\\\left( {ABC'} \right) \supset C'F \bot AB\\\left( {ABC} \right) \supset CF \bot AB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ABC} \right);\left( {ABC'} \right)} \right) = \angle CFC' = {60^0}\). Xét tam giác \(ABC\) vuông cân tại \(C\) có \(AB = 2a \Rightarrow CF = \dfrac{1}{2}AB = a\). Xét \(\Delta CC'F\) có: \(CC' = CF.\tan {60^0} = a\sqrt 3 .\) Xét \(\Delta ANC\) và \(\Delta MEC'\) có \(\angle C = \angle C' = {90^0}\), \(AC\parallel A'C',\,\,AN\parallel ME\) \( \Rightarrow \angle CAN = \angle C'ME\). \( \Rightarrow \Delta ANC \sim \Delta MEC'\,\,\left( {g.g} \right)\) theo tỉ số \(k = \dfrac{{AC}}{{MC'}} = 2\). \( \Rightarrow {S_{ANC}} = {k^2}{S_{MEC'}} = 4{S_{MEC'}}\). Ta có: \({S_{ABC}} = \dfrac{1}{2}AB.FC = \dfrac{1}{4}A{B^2} = \dfrac{1}{4}{\left( {2a} \right)^2} = {a^2}\). \( \Rightarrow S = {S_{ANC}} = \dfrac{1}{2}{S_{ABC}} = \dfrac{1}{2}{a^2}\) và \(S' = {S_{MEC'}} = \dfrac{1}{4}.{S_{ANC}} = \dfrac{1}{8}{a^2}\) Thể tích khối chóp cụt \(ANC.MEC'\) là: \({V_1} = \dfrac{h}{3}\left( {S + S' + \sqrt {S.S'} } \right)\)\( = \dfrac{{a\sqrt 3 }}{3}.\left( {\dfrac{1}{2}{a^2} + \dfrac{1}{8}{a^2} + \sqrt {\dfrac{1}{2}{a^2}.\dfrac{1}{8}{a^2}} } \right)\)\( = \dfrac{{7\sqrt 3 }}{{24}}{a^3}.\) Thể tích khối lăng trụ là: \({V_{ABC.A'B'C'}} = CC'.{S_{ABC}} = a\sqrt 3 .{a^2} = {a^3}\sqrt 3 \). \( \Rightarrow {V_2} = {V_{ABC.A'B'C'}} - {V_1} = \dfrac{{17\sqrt 3 {a^3}}}{{24}}\). Vậy thể tích của phần nhỏ hơn bằng \(\dfrac{{7\sqrt 3 }}{{24}}{a^3}.\) Chọn A. Câu hỏi 29 : Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác cân tại \(A\) có \(AB = AC = 2a,\) \(\angle CAB = {120^0}.\) Mặt phẳng \(\left( {AB'C'} \right)\) tạo với đáy một góc \({60^0}\). Thể tích khối lăng trụ là:
Đáp án: D Phương pháp giải: - Xác định góc giữa hai mặt phẳng \(\left( {AB'C'} \right)\) và \(\left( {A'B'C'} \right)\): góc giữa hai mặt phẳng là góc giữa hai đường thẳng nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến. - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính độ dài đường cao \(h = AA'\). - Tính diện tích đáy \({S_{A'B'C'}}\), sử dụng công thức \(S = \frac{1}{2}ab\sin C\). - Tính thể tích khối lăng trụ \(V = Sh\). Lời giải chi tiết:
Gọi \(D\) là trung điểm của \(B'C'\). Vì tam giác \(A'B'C'\) cân tại \(A'\) nên \(A'D \bot B'C'\) (trung tuyến đồng thời là đường cao). Ta có: \(\left. \begin{array}{l}A'D \bot B'C'\\AA' \bot B'C'\end{array} \right\} \Rightarrow B'C' \bot \left( {AA'D} \right) \Rightarrow B'C' \bot AD\) \(\left\{ \begin{array}{l}\left( {AB'C'} \right) \cap \left( {A'B'C'} \right) = B'C'\\\left( {AB'C'} \right) \supset AD \bot B'C'\\\left( {A'B'C'} \right) \supset A'D \bot B'C'\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {AB'C'} \right);\left( {A'B'C'} \right)} \right) = \angle \left( {AD;A'D} \right) = \angle ADA' = {60^0}.\) Vì tam giác \(A'B'C'\) cân tại \(A'\) nên \(\angle DA'C' = \frac{1}{2}\angle B'A'C' = {60^0}\) (trung tuyến đồng thời là phân giác). Xét tam giác vuông \(A'C'D\) có: \(A'D = A'C'.cos{60^0} = 2a.\frac{1}{2} = a.\) Xét tam giác vuông \(AA'D\) có: \(AA' = A'D.\tan {60^0} = a.\sqrt 3 .\) Ta có: \({S_{ABC}} = \frac{1}{2}AB.AC.\sin \angle BAC = \frac{1}{2}.2a.2a.\frac{{\sqrt 3 }}{2} = {a^2}\sqrt 3 .\) Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = a\sqrt 3 .{a^2}\sqrt 3 = 3{a^3}.\) Chọn D. Câu hỏi 30 : Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\)là tam giác vuông tại \(B\), \(\angle ACB = {60^0}\), cạnh \(BC = a\), đường chéo \(A'B\) tạo với mặt phẳng \(\left( {ABC} \right)\) một góc \({30^0}\). Thể tích khối lăng trụ \(ABC.A'B'C'\) là:
Đáp án: A Phương pháp giải: - Xác định góc giữa đường thẳng \(A'B\) và mặt phẳng \(\left( {ABC} \right)\): góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng. - Tính độ dài đường cao \(AA'\) và diện tích đáy \({S_{\Delta ABC}}\). - Tính thể tích khối lăng trụ theo công thức \(V = Sh\). Lời giải chi tiết:
Vì \(AA' \bot \left( {ABC} \right) \Rightarrow AB\) là hình chiếu vuông góc của \(A'B\) lên \(\left( {ABC} \right)\). \( \Rightarrow \angle \left( {A'B;\left( {ABC} \right)} \right) = \angle \left( {A'B;AB} \right) = \angle A'BA = {30^0}\) Xét tam giác vuông \(ABC\) vuông tại \(B\), \(BC = a\), \(\angle ACB = {60^0}\) có: \(AB = BC.\tan {60^0} = a\sqrt 3 .\) Vì \(AA' \bot \left( {ABC} \right) \supset AB \Rightarrow AA' \bot AB \Rightarrow \Delta ABA'\) vuông tại \(A\). \(\begin{array}{l} \Rightarrow AA' = AB.\tan \angle A'BA\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = a\sqrt 3 .\tan {30^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = a\sqrt 3 .\frac{1}{{\sqrt 3 }} = a\end{array}\) Có \({S_{\Delta ABC}} = \frac{1}{2}AB.BC = \frac{1}{2}a\sqrt 3 .a = \frac{{{a^2}\sqrt 3 }}{2}.\) Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}} = a.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{2}.\) Chọn A. Câu hỏi 31 : Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(B\) với \(AB = a,\) \(AA' = 2a,\)\(A'C = 3a\). Gọi \(M\) là trung điểm của \(A'C'\), \(I\) là giao điểm của đường thẳng \(AM\) và \(A'C\). Tính theo \(a\) thể tích khối \(IABC\).
Đáp án: C Phương pháp giải: +) So sánh thể tích của khối tứ diện \(IABC\) với thể tích của khối lăng trụ. +) Tính thể tích khối lăng trụ. Lời giải chi tiết:
Ta có: \(A'M\parallel AC \Rightarrow \dfrac{{A'M}}{{AC}} = \dfrac{{A'I}}{{IC}} = \dfrac{1}{2} \Rightarrow \dfrac{{IC}}{{A'C}} = \dfrac{2}{3}.\) Vì \(IA' \cap \left( {ABC} \right) = C\)\( \Rightarrow \dfrac{{d\left( {I;\left( {ABC} \right)} \right)}}{{d\left( {A';\left( {ABC} \right)} \right)}} = \dfrac{{IC}}{{A'C}} = \dfrac{2}{3}.\) \(\begin{array}{l} \Rightarrow \dfrac{{{V_{I.ABC}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{\dfrac{1}{3}d\left( {I;\left( {ABC} \right)} \right).{S_{ABC}}}}{{d\left( {A';\left( {ABC} \right)} \right).{S_{ABC}}}} = \dfrac{1}{3}.\dfrac{2}{3} = \dfrac{2}{9}\\ \Rightarrow {V_{I.ABC}} = \dfrac{2}{9}{V_{ABC.A'B'C'}}\end{array}\) Ta có: \(AA' \bot \left( {ABC} \right) \Rightarrow AA' \bot AC \Rightarrow \Delta AA'C\) vuông tại \(A\). \( \Rightarrow AC = \sqrt {A'{C^2} - AA{'^2}} = \sqrt {9{a^2} - 4{a^2}} = a\sqrt 5 .\) Xét tam giác vuông ABC có: \(BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {5{a^2} - {a^2}} = 2a.\) \( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}a.2a = {a^2}.\) \( \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = 2a.{a^2} = 2{a^3}.\) Vậy \({V_{I.ABC}} = \dfrac{2}{9}{V_{ABC.A'B'C'}} = \dfrac{2}{9}.2{a^3} = \dfrac{{4{a^3}}}{9}.\) Chọn C. Câu hỏi 32 : Cho hình chóp tứ giác đều \(S.ABCD\) có \(SA = a\sqrt {11} ,\) côsin góc tạo bởi hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\) bằng \(\dfrac{1}{{10}}\). Thể tích của khối chóp \(S.ABCD\) bằng:
Đáp án: C Phương pháp giải: - Hình chóp tứ giác đều có các cạnh bên bằng nhau, các cạnh đáy bằng nhau và hình chiếu vuông góc của đỉnh xuống mặt đáy trùng với tâm của đáy. - Tìm góc tạo bởi giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\) để tính cạnh đáy và chiều cao của khối chóp. - Thể tích của khối chóp có chiều cao bằng \(h,\) diện tích đáy bằng \(S\) là \(V = \dfrac{1}{3}Sh\). Lời giải chi tiết:
Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Do \(S.ABCD\) là hình chóp tứ giác đều nên \(ABCD\) là hình vuông, \(O\) là tâm của đáy nên \(SO \bot \left( {ABCD} \right)\). Trong mp \(\left( {SCD} \right)\), kẻ \(DH \bot SC\,\,\,\left( {H \in SC} \right)\,\,\,\,\,\left( 1 \right)\), ta có: \(ABCD\) là hình vuông nên \(AC \bot BD\) \(\left\{ \begin{array}{l}AC \bot BD\\SO \bot \left( {ABCD} \right) \Rightarrow SO \bot BD\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\,\,\,\,\,\left( 2 \right)\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(SC \bot \left( {DBH} \right) \Rightarrow SC \bot BH\) Do đó, góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\) là góc giữa 2 đường thẳng \(DH\) và \(BH\). Lại có hai tam giác \(SBC\) và \(SCD\) là 2 tam giác cân bằng nhau. Suy ra\(DH = BH\) Gọi độ dài cạnh của hình vuông \(ABCD\) là \(x\,\,\,\left( {x > 0} \right)\). Suy ra \(BD = AC = \sqrt 2 x\) Gọi \(M\) là trung điểm \(DC\) thì \(DM = MC = \dfrac{x}{2}\) Tam giác \(SCD\) cân tại \(S\) nên \(SM \bot CD\) Theo định lí Pi – ta – go ta có: \(SM = \sqrt {S{D^2} - D{M^2}} = \sqrt {11{a^2} - \dfrac{{{x^2}}}{4}} \) Do đó, \({S_{\Delta SCD}} = \dfrac{1}{2}SM.CD = \dfrac{1}{2}x.\sqrt {11{a^2} - \dfrac{{{x^2}}}{4}} \) Suy ra \(BH = DH = \dfrac{{2{S_{\Delta SCD}}}}{{SC}} = \dfrac{{x.\sqrt {11{a^2} - \dfrac{{{x^2}}}{4}} }}{{\sqrt {11} a}} = x.\sqrt {1 - \dfrac{{{x^2}}}{{44{a^2}}}} \) Theo giả thiết ta có: \(\cos \left( {\left( {SBC} \right);\left( {SCD} \right)} \right) = \dfrac{1}{{10}} \Rightarrow \cos BHD = \pm \dfrac{1}{{10}}\) Ta có: \(\begin{array}{l}\cos DHB = \dfrac{{D{H^2} + B{H^2} - B{D^2}}}{{2DH.BH}} = \dfrac{{2.{x^2}.\left( {1 - \dfrac{{{x^2}}}{{44{a^2}}}} \right) - 2{x^2}}}{{2{x^2}\left( {1 - \dfrac{{{x^2}}}{{44{a^2}}}} \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{2{x^2}.\dfrac{{ - {x^2}}}{{44{a^2}}}}}{{\dfrac{{2{x^2}\left( {44{a^2} - {x^2}} \right)}}{{44{a^2}}}}} = \dfrac{{ - {x^2}}}{{44{a^2} - {x^2}}}\\ \Rightarrow \left[ \begin{array}{l}\dfrac{{{x^2}}}{{{x^2} - 44{a^2}}} = \dfrac{1}{{10}}\\\dfrac{{{x^2}}}{{{x^2} - 44{a^2}}} = - \dfrac{1}{{10}}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} = - \dfrac{{44}}{9}{a^2}\\{x^2} = 4{a^2}\end{array} \right. \Leftrightarrow x = 2a\end{array}\) Suy ra \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {11{a^2} - {{\left( {\sqrt 2 a} \right)}^2}} = 3a.\) Thể tích của khối chóp đã cho là:\({S_{ABCD}} = \dfrac{1}{3}.SO.A{B^2} = \dfrac{1}{3}.3a.{\left( {2a} \right)^2} = 4{a^3}.\) Chọn C. Câu hỏi 33 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\sqrt 3 \). Gọi \(M,\,\,N\) lần lượt là trung điểm của cạnh \(SB\) và \(SD\); mặt phẳng \(\left( {AMN} \right)\) cắt \(SC\) tại \(I\). Tính thể tích khối đa diện \(ABCDMNI\).
Đáp án: A Phương pháp giải: - Tính tỉ số \(\dfrac{{SI}}{{SC}}\). - Sử dụng công thức tỉ số thể tích: Cho tứ diện\(S.ABC\). Các điểm \(M,N,P\) lần lượt nằm trên các cạnh \(SA,\,\,SB,\,\,SC\) thì \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}}.\) - Tính tỉ số thể tích \(\dfrac{{{V_{S.ANMI}}}}{{{V_{S.ABCD}}}}\) để tính thể tích khối \(ABCDMNI\). Lời giải chi tiết:
Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Trong mặt phẳng \(\left( {SBD} \right),\) gọi \(K = SO \cap MN\). Trong mặt phẳng \(\left( {SAC} \right),\) gọi \(I = AK \cap SC\), suy ra \(I\) chính là giao điểm của \(SC\) và \(mp\left( {AMN} \right)\). Ta có: \(MN\) là đường trung bình trong tam giác \(SBD\), suy ra \(\left\{ \begin{array}{l}MN\parallel BD\\MN = \dfrac{1}{2}BD\end{array} \right.\) \( \Rightarrow NK\parallel DO \Rightarrow \dfrac{{SK}}{{SO}} = \dfrac{{SN}}{{SD}} = \dfrac{1}{2}.\) Áp dụng định lí Menelaus vào tam giác \(SOC\) có cát tuyến \(AKI\): \(\dfrac{{SI}}{{IC}}.\dfrac{{AC}}{{AO}}.\dfrac{{KO}}{{KS}} = 1 \Leftrightarrow \dfrac{{SI}}{{IC}}.2.1 = 1\)\( \Rightarrow \dfrac{{SI}}{{IC}} = \dfrac{1}{2} \Rightarrow \dfrac{{SI}}{{SC}} = \dfrac{1}{3}\) Ta có: \(\begin{array}{l}\dfrac{{{V_{S.ANI}}}}{{{V_{S.ADC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SN}}{{SD}}.\dfrac{{SI}}{{SC}} = 1.\dfrac{1}{2}.\dfrac{1}{3} = \dfrac{1}{6}\\ \Rightarrow {V_{S.ANI}} = \dfrac{1}{6}{V_{S.ADC}} = \dfrac{1}{{12}}{V_{S.ABCD}}\\\dfrac{{{V_{S.AIM}}}}{{{V_{S.ACB}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SI}}{{SC}}.\dfrac{{SM}}{{SB}} = 1.\dfrac{1}{3}.\dfrac{1}{2} = \dfrac{1}{6}\\ \Rightarrow {V_{S.AIM}} = \dfrac{1}{6}{V_{S.ADC}} = \dfrac{1}{{12}}{V_{S.ABCD}}\\ \Rightarrow {V_{S.ANIM}} = {V_{S.ANI}} + {V_{AIM}} = \dfrac{1}{{12}}{V_{S.ABCD}} + \dfrac{1}{{12}}{V_{S.ABCD}} = \dfrac{1}{6}{V_{S.ABCD}}\\ \Rightarrow {V_{ABCDMNI}} = {V_{S.ABCD}} - {V_{S.ANIM}} = \dfrac{5}{6}{V_{S.ABCD}}.\end{array}\) Thể tích của khối chóp \(S.ABCD\)là: \({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.a\sqrt 3 .{a^2} = \dfrac{{\sqrt 3 {a^3}}}{3}.\) Vậy thể tích của khối đa diện \(ABCDMNI\) là: \({V_{ABCDMNI}} = \dfrac{5}{6}{V_{S.ABCD}} = \dfrac{{5\sqrt 3 {a^3}}}{{18}}.\) Chọn A. Câu hỏi 34 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\) và \(SA\) vuông góc với đáy. Biết khoảng cách giữa \(AC\) và \(SB\) bằng \(a\). Tính thể tích khối chóp \(S.ABCD\).
Đáp án: B Phương pháp giải: - Khoảng cách giữa hai đường thẳng chéo nhau \(d\) và \(d'\) là khoảng cách từ 1 điểm trên \(d\) tới mặt phẳng \(\left( \alpha \right)\) đi qua \(d'\) và song song với \(d\). - Dựa vào khoảng cách giữa \(AC\) và \(SB\) để tính độ dài \(SA\) và thể tích khối chóp. Lời giải chi tiết:
Qua \(B\), kẻ \(BE\parallel AC\,\,\left( {E \in DC} \right)\). Ta có: \(AC\parallel \left( {SBE} \right) \supset SB\). Suy ra \(d\left( {AC;SB} \right) = d\left( {AB;\left( {SBE} \right)} \right) = d\left( {A;\left( {SBE} \right)} \right).\) Qua \(A,\) kẻ \(AH \bot BE\,\,\,\,\left( {H \in BE} \right);\)\(AK \bot SH\left( {K \in SH} \right)\). Ta có: \(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BE\\AH \bot BE\end{array} \right\} \Rightarrow BE \bot \left( {SAH} \right) \Rightarrow BE \bot AK\\AK \bot AH \Rightarrow AK \bot \left( {SBE} \right)\\ \Rightarrow d\left( {AC;SB} \right) = d\left( {A;\left( {SBE} \right)} \right) = AK\\ \Rightarrow AK = a.\end{array}\) Vì \(BE\parallel AC \Rightarrow \angle CBE = \angle ACB = {45^0}\) (so le trong). \(\begin{array}{l} \Rightarrow \angle ABH = {180^0} - \angle ABC - \angle CBE\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {180^0} - {90^0} - {45^0} = {45^0}.\end{array}\) Do đó, tam giác \(AHB\) vuông cân tại \(H\). Suy ra \(AH = HB = \dfrac{{AB}}{{\sqrt 2 }} = \sqrt 2 a.\) Tam giác \(SAH\) vuông tại \(A\) có đường cao \(AK\) nên: \(\dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{S^2}}} + \dfrac{1}{{A{H^2}}}\) (Hệ thức lượng) \( \Leftrightarrow \dfrac{1}{{{a^2}}} = \dfrac{1}{{A{S^2}}} + \dfrac{1}{{{{\left( {\sqrt 2 a} \right)}^2}}} \Rightarrow SA = a\sqrt 2 .\) Vậy thể tích của khối chóp đã cho là: \({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.\sqrt 2 a.{\left( {2a} \right)^2} = \dfrac{{4\sqrt 2 {a^3}}}{3}.\) Chọn B. Câu hỏi 35 : Cho khối chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\), \(SA = SB = \sqrt 2 a\), khoảng cách từ \(A\) đến mặt phẳng \(\left( {SCD} \right)\) bằng \(a\). Thể tích của khối chóp đã cho bằng:
Đáp án: C Phương pháp giải: - Gọi \(E,\,\,F\) lần lượt là trung điểm của \(AB,\,\,CD\). Chứng minh \(CD \bot \left( {SEF} \right)\), từ đó xác định \(d\left( {E;\left( {SCD} \right)} \right)\). - Đổi đỉnh \(A\) sang đỉnh \(E\). - Trong \(\left( {SEF} \right)\) kẻ \(SH \bot EF\), chứng minh \(SH \bot \left( {ABCD} \right)\). - Chứng minh \(SE = 2SH\), đặt \(SH = x\), sử dụng định lí Pytago suy ra phương trình của \(x\) theo \(a\). - Giải \(x\) theo \(a\). - Thể tích khối chóp \(V = \dfrac{1}{3}SH.{S_{ABCD}}\). Lời giải chi tiết:
Gọi \(E,\,\,F\) lần lượt là trung điểm của \(AB,\,\,CD\). Vì tam giác \(SAB\) cân tại \(S\) nên \(SE \bot AB\). Ta có: \(\left\{ \begin{array}{l}AB \bot SE\\AB \bot EF\end{array} \right. \Rightarrow AB \bot \left( {SEF} \right)\). Mà \(CD\parallel AB\) nên \(CD \bot \left( {SEF} \right)\). Trong \(\left( {SEF} \right)\), kẻ \(SH \bot EF\,\,\left( {H \in EF} \right).\) Ta có: \(\left\{ \begin{array}{l}CD \bot \left( {ESF} \right) \Rightarrow CD \bot SH\\SH \bot EF\end{array} \right.\)\( \Rightarrow SH \bot \left( {ABCD} \right).\) Cũng trong \(\left( {SEF} \right)\) ta kẻ \(EK \bot SF\,\,\left( {K \in SF} \right).\) Khi đó ta có: \(\left\{ \begin{array}{l}EK \bot CD\,\,\,\,\left( {CD \bot \left( {SEF} \right)} \right)\\EK \bot SF\end{array} \right.\) \( \Rightarrow EK \bot \left( {SCD} \right).\) \( \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = d\left( {E;\left( {SCD} \right)} \right) = EK = a\) (do \(AE\parallel \left( {SCD} \right)\)). Ta có: \({S_{SEF}} = \dfrac{1}{2}SH.EF{\rm{ = }}\dfrac{1}{2}.EK.SF\). \( \Rightarrow SH.2a = SF.a \Leftrightarrow SF = 2SH\). Áp dụng định lí Pytago trong tam giác vuông \(SAE\) ta có: \(SE = \sqrt {S{A^2} - A{E^2}} = \sqrt {2{a^2} - {a^2}} = a\). Đặt \(SH = x \Rightarrow SF = 2x\). Áp dụng định lí Pytago trong các tam giác vuông ta có: \(\begin{array}{l}EH = \sqrt {S{E^2} - S{H^2}} = \sqrt {{a^2} - {x^2}} \\FH = \sqrt {S{F^2} - S{H^2}} = \sqrt {4{x^2} - {x^2}} = x\sqrt 3 \end{array}\) Mà \(EH + FH = EF = 2a\) \(\begin{array}{l} \Rightarrow \sqrt {{a^2} - {x^2}} + x\sqrt 3 = 2a\\ \Leftrightarrow {a^2} - {x^2} = {\left( {2a - x\sqrt 3 } \right)^2}\\ \Leftrightarrow {a^2} - {x^2} = 4{a^2} - 4\sqrt 3 ax + 3{x^2}\\ \Leftrightarrow 3{a^2} - 4\sqrt 3 ax + 4{x^2} = 0\\ \Leftrightarrow {\left( {a\sqrt 3 - 2x} \right)^2} = 0\\ \Leftrightarrow 2x = a\sqrt 3 \\ \Leftrightarrow x = \dfrac{{a\sqrt 3 }}{2} = SH\end{array}\) Vậy thể tích khối chóp \(S.ABCD\) là \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2}.{\left( {2a} \right)^2} = \dfrac{{2{a^3}\sqrt 3 }}{3}\). Chọn C. Câu hỏi 36 : Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(K\) là trung điểm của \(SC\). Mặt phẳng qua \(AK\) cắt các cạnh \(SB,\,\,SD\) lần lượt tại \(M,\,\,N\). Gọi \({V_1},\,\,V\) thứ tự là thể tích của khối chóp \(S.AMKN\) và khối chóp \(S.ABCD\). Giá trị nhỏ nhất của tỷ số \(\dfrac{{{V_1}}}{V}\) bằng
Đáp án: D Phương pháp giải: - Xác định các điểm \(M,\,\,N\). - Đặt \(\dfrac{{SM}}{{SB}} = x,\,\,\,\dfrac{{SN}}{{SD}} = y\), tính tỉ số thể tích \(\dfrac{{{V_1}}}{V}\) bằng 2 cách theo \(x,\,\,y\). - Rút \(x\) theo \(y\) hoặc ngược lại, tỉ số thể tích \(\dfrac{{{V_1}}}{V}\) lúc này chỉ được tính theo 1 ẩn \(x\) hoặc \(y\), sử dụng phương pháp hàm số để tìm GTNN của hàm số. Lời giải chi tiết:
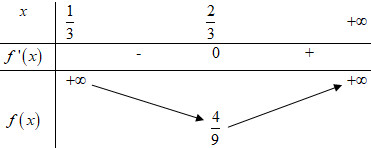
Gọi mặt phẳng chứa \(AK,\) cắt \(SB,\,\,SD\) lần lượt tại \(M,\,\,N\) là \(\left( \alpha \right)\) . Trong \(\left( {SAC} \right)\) gọi \(I = AC \cap SO\). Trong \(\left( {SBD} \right)\), lấy \(M \in SB\), nối \(MI\) cắt \(SD\) tại \(N\). Khi đó ta có \(\left( \alpha \right) \equiv \left( {AMKN} \right)\). Đặt: \(\dfrac{{SM}}{{SB}} = x,\,\,\,\dfrac{{SN}}{{SD}} = y.\) Ta có: \(\begin{array}{l}\dfrac{{{V_1}}}{V} = \dfrac{{{V_{SAMNK}}}}{{{V_{SABCD}}}} = \dfrac{1}{2}.\dfrac{{{V_{SAMK}} + {V_{SANK}}}}{{{V_{SABC}}}}\\\,\,\,\,\,\, = \dfrac{1}{2}.\left( {\dfrac{{SM}}{{SB}}.\dfrac{{SK}}{{SC}} + \dfrac{{SN}}{{SD}}.\dfrac{{SK}}{{SC}}} \right) = \dfrac{1}{4}\left( {x + y} \right)\end{array}\) Lại có: \(\begin{array}{l}\dfrac{{{V_1}}}{V} = \dfrac{{{V_{S.AMKN}}}}{{{V_{S.ABCD}}}} = \dfrac{1}{2}.\dfrac{{{V_{SAMN}} + {V_{SKMN}}}}{{{V_{SABD}}}}\\\,\,\,\,\,\,\, = \dfrac{1}{2}\left( {\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}} + \dfrac{{SK}}{{SC}}.\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}}} \right)\\\,\,\,\,\,\,\, = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}}.\left( {\dfrac{1}{2} + \dfrac{1}{2}.\dfrac{{SK}}{{SC}}} \right) = \dfrac{3}{4}xy\end{array}\) Từ đó ta có: \( \Rightarrow \dfrac{3}{4}xy = \dfrac{1}{4}\left( {x + y} \right)\)\( \Rightarrow x + y = 3xy \Leftrightarrow x = y\left( {3x - 1} \right)\)\( \Rightarrow y = \dfrac{x}{{3x - 1}}\). Do \(x,\,\,y > 0 \Rightarrow 3x - 1 > 0 \Leftrightarrow x > \dfrac{1}{3}\). Khi đó ta có: \(\dfrac{{{V_1}}}{V} = \dfrac{3}{4}xy = \dfrac{3}{4}.\dfrac{{{x^2}}}{{3x - 1}}\) với \(x > \dfrac{1}{3}\). Đặt \(f\left( x \right) = \dfrac{{{x^2}}}{{3x - 1}}\) ta có: \(\begin{array}{l}f'\left( x \right) = \dfrac{{2x\left( {3x - 1} \right) - 3{x^2}}}{{{{\left( {3x - 1} \right)}^2}}} = \dfrac{{x\left( {3x - 2} \right)}}{{{{\left( {3x - 1} \right)}^2}}}\\f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\,\left( {ktm} \right)\\x = \dfrac{2}{3}\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Bảng biến thiên:
Dựa vào BBT ta thấy: \(\mathop {\min }\limits_{\left( {\dfrac{1}{3}; + \infty } \right)} f\left( x \right) = f\left( {\dfrac{2}{3}} \right) = \dfrac{4}{9}\). Vậy giá trị nhỏ nhất của \(\dfrac{{{V_1}}}{V}\) là \(\dfrac{3}{4}.\dfrac{4}{9} = \dfrac{1}{3}\), đạt được khi \(\dfrac{{SM}}{{SB}} = \dfrac{{SN}}{{SD}} = \dfrac{2}{3}\). Chọn D. Câu hỏi 37 : Cho lăng trụ đứng \(ABC.A'B'C'\) với \(ABC\) là tam giác vuông cân tại \(C\) có \(AB = a\) , mặt bên \(ABB'A'\) là hình vuông. Mặt phẳng qua trung điểm \(I\) của \(AB\) và vuông góc với \(AB'\) chi khối lăng trụ thành 2 phần. Tính thể tích mỗi phần?
Đáp án: C Phương pháp giải: - Dựng mặt phẳng đi qua \(I\) và vuông góc với \(AB'\) (là mặt phẳng \(\left( {DIC} \right)\) với \(D\) là trung điểm của \(AA'\). - Tính diện tích tam giác \(ABC\), từ đó suy ra diện tích tam giác \(AIC\). - Tính độ dài đường cao \(A'A\) của lăng trụ và độ dài đường cao \(DA\) của hình chóp \(D.AIC\). - Tính thể tích khối lăng trụ \(ABC.A'B'C'\) và khối chóp \(D.AIC\), từ đó tính được thể tích phần còn lại của khối lăng trụ được chia bởi mặt phẳng \(\left( {DIC} \right)\) Lời giải chi tiết:
Gọi \(D\) là trung điểm của \(AA'\) ta có \(ID\) là đường trung bình của tam giác \(AA'B\)\( \Rightarrow ID\parallel A'B\). Mà \(A'B \bot AB'\) (do \(ABB'A'\) là hình vuông) \( \Rightarrow ID \bot AB'\) Tam giác \(ABC\) vuông cân tại \(C\) nên \(IC \bot AB\). Mà \(AA' \bot \left( {ABC} \right) \Rightarrow AA' \bot IC\) \( \Rightarrow IC \bot \left( {ABB'A'} \right) \Rightarrow IC \bot AB'\) \( \Rightarrow AB' \bot \left( {ICD} \right)\) \( \Rightarrow \) Mặt phẳng qua \(I\) và vuông góc với \(AB'\) là \(\left( {ICD} \right).\) Tam giác \(ABC\) vuông cân tại \(C\) nên \(AC = BC = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{a}{{\sqrt 2 }}\). \( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AC.BC = \dfrac{1}{2}\dfrac{a}{{\sqrt 2 }}\dfrac{a}{{\sqrt 2 }} = \dfrac{{{a^2}}}{4}\). Vì \(ABB'A'\) là hình vuông \( \Rightarrow AA' = AB = a.\) \( \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = a.\dfrac{{{a^2}}}{4} = \dfrac{{{a^3}}}{4} = V\) Ta có: \(\begin{array}{l}{V_{D.ACI}} = \dfrac{1}{3}AD.{S_{ACI}} = \dfrac{1}{3}.\dfrac{1}{2}AA'.\dfrac{1}{2}{S_{ABC}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{{12}}{V_{ABC.A'B'C'}} = \dfrac{1}{{12}}.\dfrac{{{a^3}}}{4} = \dfrac{{{a^3}}}{{48}} = {V_1}\end{array}\) \( \Rightarrow {V_2} = V - {V_1} = \dfrac{{{a^3}}}{4} - \dfrac{{{a^3}}}{{48}} = \dfrac{{11{a^3}}}{{48}}.\) Chọn C. Câu hỏi 38 : Cho một tứ diện đều \(S.ABC\) có chiều cao h. Ở ba góc của tứ diện, người ta cắt đi các tứ diện đều có chiều cao x để khối đa diện còn lại có thể tích bằng một nửa thể tích khối tứ diện đều ban đầu. Tìm x.
Đáp án: D Phương pháp giải: Chiều cao của khối tứ diện đều cạnh a là: \(h = \dfrac{{a\sqrt 6 }}{3}\) Thể tích của khối tứ diện đều cạnh a là: \(V = \dfrac{{{a^3}\sqrt 2 }}{{12}}\) Lời giải chi tiết:
Tứ diện đều .. có chiều cao h \( \Rightarrow \) Độ dài cạnh của tứ diện \(S.ABC\) là: \(\dfrac{{3h}}{{\sqrt 6 }} = \dfrac{{h\sqrt 6 }}{2}\) \( \Rightarrow \) Thể tích của khối tứ diện \(S.ABC\) là: \({V_{S.ABC}} = \dfrac{{{{\left( {\dfrac{{h\sqrt 6 }}{2}} \right)}^3}\sqrt 2 }}{{12}} = \dfrac{{{h^3}.6\sqrt 6 .\sqrt 2 }}{{8.12}} = \dfrac{{{h^3}\sqrt 3 }}{8}\) Tổng thể tích của ba khối tứ diện đều bị cắt đi là: \({V_0} = 3.\dfrac{{{x^3}\sqrt 3 }}{8}\) Vì thể tích phần còn lại bằng một nửa thể tích khối tứ diện đều ban đầu nên, ta có: \(\dfrac{{3{x^3}\sqrt 3 }}{8} = \dfrac{1}{2}.\dfrac{{{h^3}\sqrt 3 }}{8} \Leftrightarrow 6{x^3} = {h^3} \Leftrightarrow x = \dfrac{h}{{\sqrt[3]{6}}}\) Chọn D. Câu hỏi 39 : Cho hình lăng trụ \(ABC.A'B'C'\) có độ dài cạnh bên bằng \(a\), đáy \(ABC\) là tam giác vuông tại \(B\), \(\angle BCA = {60^0}\), góc giữa \(AA'\) và \(\left( {ABC} \right)\) bằng \({60^0}\). Hình chiếu vuông góc của \(A'\) lên \(\left( {ABC} \right)\) trùng với trọng tâm \(\Delta ABC\). Tính theo \(a\) thể tích của khối lăng trụ \(ABC.A'B'C'\).
Đáp án: C Phương pháp giải: Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P). Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Lời giải chi tiết:
Gọi G là trọng tâm tam giác ABC. Theo đề bài, ta có : \(A'G \bot \left( {ABC} \right)\). \( \Rightarrow \angle \left( {AA';\left( {ABC} \right)} \right) = \angle GAA' = {60^0}\) \( \Rightarrow \left\{ \begin{array}{l}AG = AA'.{\rm{cos6}}{{\rm{0}}^0} = \dfrac{a}{2} \Rightarrow AN = \dfrac{3}{2}.\dfrac{a}{2} = \dfrac{{3{\rm{a}}}}{4}\\A'G = AA'.{\rm{sin6}}{{\rm{0}}^0} = \dfrac{{a\sqrt 3 }}{2}\end{array} \right.\) Giả sử độ dài đoạn \(BC = x\) \( \Rightarrow BN = \dfrac{x}{2},\,AB = BC.\tan \angle C = \tan {60^0}.x = x\sqrt 3 \) \( \Rightarrow AN = \sqrt {{{\left( {\dfrac{x}{2}} \right)}^2} + {{\left( {x\sqrt 3 } \right)}^2}} = \dfrac{{x\sqrt {13} }}{2}\) \(\begin{array}{l} \Rightarrow \dfrac{{x\sqrt {13} }}{2} = \dfrac{{3{\rm{a}}}}{4} \Rightarrow x = \dfrac{{3a}}{{2\sqrt {13} }} = \dfrac{{3\sqrt {13} }}{{26}}\\ \Rightarrow BC = \dfrac{{3a\sqrt {13} }}{{26}},\,\,AB = \dfrac{{3a\sqrt {13} }}{{26}}.\sqrt 3 = \dfrac{{3a\sqrt {39} }}{{26}}\\ \Rightarrow {S_{ABC}} = \dfrac{1}{2}.AB.BC = \dfrac{1}{2}.\dfrac{{3a\sqrt {13} }}{{26}}.\dfrac{{3a\sqrt {39} }}{{26}} = \dfrac{{9{a^2}\sqrt 3 }}{{104}}\end{array}\) Thể tích của khối lăng trụ ABC.A’B’C’ là: \(V = {S_{ABC}}.A'G = \dfrac{{9{a^2}\sqrt 3 }}{{104}}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{27{a^3}}}{{208}}\) Chọn C. Câu hỏi 40 : Cho hình chóp \(S.ABC\) có \(SA = a\), \(SB = 3a\sqrt 2 \), \(SC = 2a\sqrt 3 \), \(\angle ASB = \angle BSC = \angle CSA = {60^0}\). Thể tích khối chóp \(S.ABC\) là:
Đáp án: C Phương pháp giải: * Sử dụng công thức tỉ số thể tích cho khối chóp tam giác (Công thức Simson): Cho khối chóp S.ABC, các điểm \({A_1},\,{B_1},\,{C_1}\) lần lượt thuộc \(SA,\,SB,\,SC\). Khi đó, \(\dfrac{{{V_{S.\,{A_1}{B_1}{C_1}}}}}{{{V_{S.ABC}}}} = \dfrac{{S{A_1}}}{{SA}}.\dfrac{{S{B_1}}}{{SB}}.\dfrac{{S{C_1}}}{{SC}}\)
* Công thức thể tích khối tứ diện đều cạnh a là: \(V = \dfrac{{{a^3}\sqrt 2 }}{{12}}\). Lời giải chi tiết: Trên các cạnh SB, SC lần lượt lấy B’, C’ sao cho \(SB' = SC' = SA = a\) Lại có: \(\angle {\rm{AS}}B' = \angle B'SC' = \angle C'SA = {60^0}\)\( \Rightarrow SAB'C'\) là tứ diện đều cạnh a \( \Rightarrow {V_{SAB'C'}} = \dfrac{{{a^3}\sqrt 2 }}{{12}}\) Ta có: \(\dfrac{{{V_{S.\,AB'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}} = \dfrac{a}{{3{\rm{a}}\sqrt 2 }}.\dfrac{a}{{2{\rm{a}}\sqrt 3 }} = \dfrac{1}{{6\sqrt 6 }}\)\( \Rightarrow {V_{S.ABC}} = 6\sqrt 6 .{V_{S.AB'C'}} = 6\sqrt 6 .\dfrac{{{a^3}\sqrt 2 }}{{12}} = {a^3}\sqrt 3 .\) Chọn C. Câu hỏi 41 : Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(A,\,AC = 2\sqrt 2 \), biết góc giữa \(AC'\) và \(\left( {ABC} \right)\) bằng \({60^0}\) và \(AC' = 4\). Tính thể tích V của khối lăng trụ \(ABC.A'B'C'\).
Đáp án: D Phương pháp giải: Thể tích khối lăng trụ có diện tích đáy S và chiều cao h là: \(V = Sh\) Lời giải chi tiết:
\(ABC\) là tam giác vuông cân tại \(A,\,AC = 2\sqrt 2 \) \( \Rightarrow {S_{ABC}} = \dfrac{1}{2}A{C^2} = \dfrac{1}{2}.{\left( {2\sqrt 2 } \right)^2} = 4\) Do góc giữa \(AC'\) và \(\left( {ABC} \right)\) bằng \({60^0}\) nên khoảng cách từ C’ đến (ABC): \(d\left( {C';\left( {ABC} \right)} \right) = AC'.\sin {60^0} = 4.\dfrac{{\sqrt 3 }}{2} = 2\sqrt 3 \) Thể tích khối lăng trụ \(ABC.A'B'C'\) là: \(V = {S_{ABC}}.s\left( {C';\left( {ABC} \right)} \right) = 4.2\sqrt 3 = 8\sqrt 3 \). Chọn D. Câu hỏi 42 : Cho hình lăng trụ \(ABC.A'B'C'\)có đáy \(ABC\)là tam giác đều cạnh bằng a. Hình chiếu vuông góc của \(A'\)xuống mặt phẳng \(\left( {ABC} \right)\)là trung điểm của \(AB\). Mặt bên \(\left( {AA'C'C} \right)\) hợp với mặt đáy một góc bằng 450. Tính thể tích của khối lăng trụ \(ABC.A'B'C'\)theo a.
Đáp án: A Phương pháp giải: - Tìm góc giữa mặt bên \(\left( {ACC'A'} \right)\) và mặt đáy: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến. - Tính chiều cao của hình lăng trụ dựa vào tỉ số lượng giác của góc nhọn trong tam giác vuông. - Áp dụng công thức tính thể tích hình lăng trụ có chiều cao \(h\), bán kính đáy \(B\) là \(V = B.h\). Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(AB\) \( \Rightarrow A'M \bot \left( {ABC} \right)\,\,\,\left( {gt} \right).\) Gọi \(N\) là trung điểm của \(AC\). Do tam giác \(ABC\) đều cạnh \(a\) nên \(BN = \dfrac{{a\sqrt 3 }}{2}\) và \({S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\). Kẻ\(MH \bot AC\,\,\left( {H \in AC} \right)\) ta có: \(\left\{ \begin{array}{l}AC \bot A'M\,\,\left( {A'M \bot \left( {ABC} \right)} \right)\\AC \bot MH\end{array} \right.\) \( \Rightarrow AC \bot \left( {A'MH} \right)\) \( \Rightarrow AC \bot A'H\). \(\left\{ \begin{array}{l}\left( {ACC'A'} \right) \cap \left( {ABC} \right) = AC\\\left( {ACC'A'} \right) \supset A'H \bot AC\\\left( {ABC} \right) \supset MH \bot AC\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ACC'A'} \right);\left( {ABC} \right)} \right) = \angle \left( {A'H;MH} \right) = \angle A'HM = {45^0}\). Ta có: \(A'M \bot \left( {ABC} \right)\) nên \(A'M \bot MH\), khi đó tam giác \(A'MH\) vuông tại \(M\). Lại có \(MH\) là đường trung bình của tam giác \(ABN\) nên \(MH = \dfrac{1}{2}BN = \dfrac{{a\sqrt 3 }}{4}\). \( \Rightarrow A'M = MH.\tan {45^0} = \dfrac{{a\sqrt 3 }}{4}\) Vậy \({V_{ABC.A'B'C'}} = A'M.{S_{\Delta ABC}}\)\( = \dfrac{{a\sqrt 3 }}{4}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{a^3}}}{{16}}.\) Chọn A. Câu hỏi 43 : Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình chữ nhật có \(AB = 2a,\,\,BC = 4a\), \(\left( {SAB} \right) \bot \left( {ABCD} \right)\), hai mặt bên \(\left( {SBC} \right)\) và \(\left( {SAD} \right)\) cùng hợp với đáy \(ABCD\) một góc 30o .Tính thể tích hình chóp \(S.ABCD\) theo a.
Đáp án: B Phương pháp giải: - Xác định chiều cao của khối chóp: Hai mặt phẳng vuông góc với nhau, một đường nằm trong mặt này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia. - Xác định góc giữa hai mặt phẳng: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến. - Tính chiều cao \(SI\) dựa vào tỉ số lượng giác của góc nhọn trong tam giác vuông. - Áp dụng công thức tính thể tích khối chóp có chiều cao \(h\), diện tích đáy \(B\) là \(V = \dfrac{1}{3}Bh\). Lời giải chi tiết:
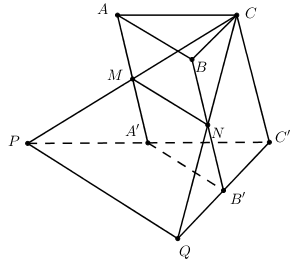
Trong \(\left( {SAB} \right)\) kẻ \(SI \bot AB\,\,\,\left( {I \in AB} \right)\) ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SAB} \right) \supset SI \bot AB\end{array} \right.\) \( \Rightarrow SI \bot \left( {ABCD} \right)\). \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SI\,\,\,\left( {SI \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\)\( \Rightarrow BC \bot SB\) Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SB \bot BC\\\left( {ABCD} \right) \supset AB \bot BC\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABCD} \right)} \right) = \angle \left( {SB;AB} \right) = \angle SBA = {30^0}\). Hoàn toàn tương tự ta chứng minh được \(\angle \left( {\left( {SAD} \right);\left( {ABCD} \right)} \right) = \angle \left( {SA;AB} \right) = \angle SAB = {30^0}\) Do đó tam giác \(SAB\) cân tại \(S\) nên \(I\) là trung điểm của \(AB\). Tam giác \(SIA\) vuông tại \(I\) có \(\angle SAB = {30^0},\,\,AI = a\)\( \Rightarrow SI = a\tan {30^0} = \dfrac{{a\sqrt 3 }}{3}.\) \({S_{ABCD}} = AB.BC = 2a.4a = 8{a^2}\). Vậy \({V_{S.ABCD}} = \dfrac{1}{3}.SI.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{3}.8{a^2} = \dfrac{{8\sqrt 3 }}{9}{a^3}.\) Chọn B. Câu hỏi 44 : Cho khối lăng trụ \(ABC.A’B’C’\) có thể tích bằng \(1\). Gọi \(M, N\) lần lượt là trung điểm của các đoạn thẳng \(AA'\) và \(BB'\). Đường thẳng \(CM\) cắt đường thẳng \(C’A'\) tại \(P\), đường thẳng \(CN\) cắt đường thẳng \(C’B'\) tại \(Q\). Thể tích của khối đa diện lồi \(A’MPB’NQ\) bằng:
Đáp án: D Phương pháp giải: Phân chia khối đa diện: \({V_{A'MPB'NQ}} = {V_{C.C'PQ}} - {V_{CC'A'B'NM}}\). Xác định các tỉ số về chiều cao và diện tích đáy để suy ra tỉ số giữa chóp, lăng trụ,… Lời giải chi tiết:
Gọi diện tích đáy, chiều cao, thể tích của hình lăng trụ \(ABC.A'B'C'\)lần lượt là \(S,\,\,h,\,\,V\)\( \Rightarrow V = Sh\). Ta có: \(\Delta PQC' \sim \Delta A'B'C'\) theo tỉ số \(2\) \( \Rightarrow {S_{C'PQ}} = 4{S_{A'B'C'}} = 4S.\) \( \Rightarrow {V_{C.C'PQ}} = \dfrac{1}{3}.h.4S = \dfrac{4}{3}V\). Ta có : \({S_{ABNM}} = \dfrac{1}{2}{S_{ABB'A'}} \Rightarrow {V_{C.ABNM}} = \dfrac{1}{2}{V_{C.ABB'A'}}\) Mà \({V_{C.ABB'A'}} = \dfrac{2}{3}V \Rightarrow {V_{C.ABNM}} = \dfrac{1}{2}.\dfrac{2}{3}V = \dfrac{V}{3}\) \( \Rightarrow {V_{CC'A'B'NM}} = V - \dfrac{V}{3} = \dfrac{2}{3}V\) Vậy \({V_{A'MPB'NQ}} = \dfrac{4}{3}V - \dfrac{2}{3}V = \dfrac{2}{3}V\). Chọn D. Câu hỏi 45 : Cho hình chóp \(S.ABC\) có đáy là tam giác cân tại \(A\), mặt bên \(\left( {SBC} \right)\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi \(\left( \alpha \right)\) là mặt phẳng đi qua điểm \(B\) và vuông góc với \(SC\), chia khối chóp thành hai phần. Tính tỉ số thể tích của hai phần đó.
Đáp án: A Phương pháp giải: - Gọi \(I\) là trung điểm của \(BC\), chứng minh \(SI \bot \left( {ABC} \right)\). - Kẻ \(IH \bot SC\), chứng minh \(SC \bot \left( {AHI} \right)\). - Qua \(B\) dựng mặt phẳng song song với \(\left( {AHI} \right)\), chứng minh đó là mặt phẳng qua \(B\) và vuông góc với \(SC\). - Sử dụng tỉ số thể tích: Cho hình chóp \(S.ABC\), các điểm \(A',\,\,B',\,\,C'\) lần lượt thuộc \(SA,\,\,SB,\,\,SC\), khi đó ta có \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\). Lời giải chi tiết:
Gọi \(I\) là trung điểm của \(BC\), do tam giác \(SBC\) đều nên \(SI \bot BC\). Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \bot \left( {ABC} \right)\\\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SI \bot BC\end{array} \right.\) \( \Rightarrow SI \bot \left( {ABC} \right)\). Vì tam giác \(ABC\) cân tại \(A\) (gt) nên \(AI \bot BC\), lại có \(AI \bot SI\) (do \(SI \bot \left( {ABC} \right)\)) nên suy ra \(AI \bot \left( {SBC} \right)\), do đó \(AI \bot SC\). Gọi \(K\) là trung điểm của \(SC\), do \(\Delta SBC\) đều nên \(BK \bot SC\), trong \(\left( {SBC} \right)\) kẻ \(IH\parallel BK\,\,\left( {H \in SC} \right)\) \( \Rightarrow IH \bot SC\). Ta có: \(\left\{ \begin{array}{l}IH \bot SC\\AI \bot SC\end{array} \right. \Rightarrow SC \bot \left( {AHI} \right)\). Trong \(\left( {SAC} \right)\) kẻ \(KN\parallel AH\,\,\left( {N \in SA} \right)\) ta có: \(\left\{ \begin{array}{l}BK\parallel IH\\KN\parallel AH\end{array} \right. \Rightarrow \left( {BKN} \right)\parallel \left( {AHI} \right)\). Mà \(SC \bot \left( {AHI} \right) \Rightarrow SC \bot \left( {BKN} \right)\). Do đó mặt phẳng qua \(B\) và vuông góc với \(SC\) chính là \(\left( {BKN} \right)\). Mặt phẳng \(\left( {BKN} \right)\) chia khối chóp đã cho thành hai phần. Đặt \({V_1} = {V_{S.BKN}}\), \({V_2} = {V_{BKN.ABC}}\). Áp dụng định lí Ta-lét ta có: \(\begin{array}{l}\dfrac{{HC}}{{HK}} = \dfrac{{IC}}{{IB}} = 1 \Rightarrow HK = HC = \dfrac{1}{2}CK = \dfrac{1}{2}SK\\ \Rightarrow \dfrac{{SK}}{{SH}} = \dfrac{2}{3} = \dfrac{{SN}}{{SA}}\\ \Rightarrow \dfrac{{{V_{SBKN}}}}{{{V_{SBCA}}}} = \dfrac{{SK}}{{SC}}.\dfrac{{SN}}{{SA}} = \dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{3}\\ \Rightarrow {V_1} = {V_{SBKN}} = \dfrac{1}{3}{V_{SBCA}} = \dfrac{1}{3}{V_{S.ABC}}\\ \Rightarrow {V_2} = \dfrac{2}{3}{V_{S.ABC}}\end{array}\) Vậy \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{1}{3}:\dfrac{2}{3} = \dfrac{1}{2}.\) Chọn A. Câu hỏi 46 : Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(M,\,\,N,\,\,P\)lần lượt nằm trên các cạnh \(A'B'\), \(B'C'\), \(BC\)sao cho \(\dfrac{{B'M}}{{A'B'}} = \dfrac{1}{2}\), \(\dfrac{{B'N}}{{B'C'}} = \dfrac{2}{3}\), \(\dfrac{{BP}}{{BC}} = \dfrac{1}{3}\). Mặt phẳng \(\left( {MNP} \right)\) chia hình lăng trụ đã cho thành 2 khối đa diện. Gọi \({V_1}\) là thể tích khối đa diện chứa đỉnh B và \({V_2}\)là thể tích phần còn lại. Tính tỷ số \(\dfrac{{{V_1}}}{{{V_2}}}\)theo a.
Đáp án: B Phương pháp giải: - Phân chia các khối đa diện. - So sánh chiều cao, diện tích đáy, từ đó suy ra tỉ số thể tích các khối đa diện so với \(V = {V_{ABC.A'B'C'}}\). Lời giải chi tiết:
Giả sử \(AB \cap \left( {MNP} \right) = Q\), khi đó ta có: \(\left( {MNP} \right) \cap \left( {ABC} \right) = PQ\). Mà \(\left( {MNP} \right) \cap \left( {A'B'C'} \right) = MN\), \(\left( {ABC} \right)\parallel \left( {A'B'C'} \right)\). \( \Rightarrow MN\parallel PQ\). Ta có: \(\) \( \Rightarrow MQ,\,\,NP,\,\,BB'\) đồng quy tại \(S\). Khi đó ta có: \({V_1} = {V_{B'MN.BQP}} = {V_{S.B'MN}} - {V_{S.BQP}}\). Đặt \(V = {V_{ABC.A'B'C'}}\). Áp dụng định lí Ta-lét ta có: \(\dfrac{{SB}}{{SB'}} = \dfrac{{BP}}{{B'N}} = \dfrac{{\dfrac{1}{3}BC}}{{\dfrac{2}{3}B'C'}} = \dfrac{1}{2}\) \( \Rightarrow B\) là trung điểm của \(SB'\). Ta có: \(\dfrac{{{S_{B'MN}}}}{{{S_{B'A'C'}}}} = \dfrac{{B'M}}{{B'A'}}.\dfrac{{B'N}}{{B'C'}} = \dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{3}\). \(\begin{array}{l} \Rightarrow \dfrac{{{V_{S.B'MN}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{1}{3}.\dfrac{{SB'}}{{BB'}}.\dfrac{{{S_{B'MN}}}}{{{S_{A'B'C'}}}} = \dfrac{1}{3}.2.\dfrac{1}{3} = \dfrac{2}{9}\\ \Rightarrow {V_{S.B'MN}} = \dfrac{2}{9}V\end{array}\) Áp dụng định lí Ta-lét ta có: \(\dfrac{{BQ}}{{BA}} = \dfrac{{BQ}}{{2BM'}} = \dfrac{1}{2}.\dfrac{{SB}}{{SB'}} = \dfrac{1}{4}\) \( \Rightarrow \dfrac{{{S_{BQP}}}}{{{S_{ABC}}}} = \dfrac{{BQ}}{{BA}}.\dfrac{{BP}}{{BC}} = \dfrac{1}{4}.\dfrac{1}{3} = \dfrac{1}{{12}}\). \(\begin{array}{l}\dfrac{{{V_{S.BQP}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{1}{3}.\dfrac{{SB}}{{BB'}}.\dfrac{{{S_{BQP}}}}{{{S_{ABC}}}} = \dfrac{1}{3}.1.\dfrac{1}{{12}} = \dfrac{1}{{36}}\\ \Rightarrow {V_{S.BQP}} = \dfrac{1}{{36}}V\end{array}\) \(\begin{array}{l} \Rightarrow {V_1} = {V_{S.B'MN}} - {V_{S.BQP}} = \dfrac{2}{9}V - \dfrac{1}{{36}}V = \dfrac{7}{{36}}V\\ \Rightarrow {V_2} = V - {V_1} = \dfrac{{29}}{{36}}V\end{array}\) Vậy \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\dfrac{7}{{36}}V}}{{\dfrac{{29}}{{36}}V}} = \dfrac{7}{{29}}.\) Chọn B. Câu hỏi 47 : Cho hình chóp tứ giác đều có mặt bên hợp với đáy một góc \({45^0}\) và khoảng cách từ chân đường cao đến mặt bên bằng \(a\). Tính thể tích của khối chóp đó?
Đáp án: B Phương pháp giải: +) Xác định góc giữa mặt bên và đáy. +) Xác định khoảng cách từ chân đường cao đến mặt bên. +) Áp dụng công thức tính thể tích \({V_{S.ABCD}} = \dfrac{1}{3}h.{S_d}\) Lời giải chi tiết:
Gọi \(H\) là tâm tam hình vuông \(ABCD \Rightarrow SH \bot \left( {ABCD} \right)\) Gọi \(E\) là trung điểm của \(BC\) ta có : \(\left\{ {\begin{array}{*{20}{l}}{BC \bot AE}\\{BC \bot SH}\end{array}} \right. \Rightarrow BC \bot \left( {SAE} \right) \Rightarrow BC \bot SE\) \( \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SE;AE} \right)} = \widehat {SEA} = {45^0}\) Trong \(\left( {SAE} \right)\) kẻ \(HK \bot SE \Rightarrow HK \bot \left( {SBC} \right) \Rightarrow HK = a\) \( \Rightarrow HE = \dfrac{{HK}}{{\cos 45}} = a\sqrt 2 \) \(\begin{array}{l} \Rightarrow AB = 2HE = 2a\sqrt 2 \Rightarrow {S_{ABCD}} = 8{a^2}\\SH = HE.\tan 45 = a\sqrt 2 \\ \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}.a\sqrt 2 .8{a^2} = \dfrac{{8{a^3}\sqrt 2 }}{3}\end{array}\) Chọn B. Câu hỏi 48 : Cho khối lăng trụ \(ABC.A'B'C'\). Gọi \(E,\,\,F\) lần lượt là trung điểm của \(AA',\,\,CC'\). Mặt phẳng \(\left( {BEF} \right)\) chia khối lăng trụ thành hai phần. Tỉ số thể tích của hai phần đó là:
Đáp án: C Phương pháp giải: Sử dụng phân chia thể tích. Sử dụng công thức tính thể tích hình chóp \(V = \dfrac{1}{3}h.S\) , thể tích lăng trụ \(V = h.S\) Lời giải chi tiết:
Ta có: \({V_{ABC.A'B'C'}} = d\left( {B;\left( {A'B'C'} \right)} \right).{S_{A'B'C'}} = V\) \({V_{B.A'B'C'}} = \dfrac{1}{3}d\left( {B;\left( {A'B'C'} \right)} \right).{S_{A'B'C'}} = \dfrac{1}{3}V\) Suy ra \({V_{B.AA'C'C}} = {V_{ABC.A'B'C'}} - {V_{B.A'B'C'}}\)\( = V - \dfrac{1}{3}V = \dfrac{2}{3}V\) Lại có: \({S_{ACFE}} = \dfrac{1}{2}{S_{AA'C'C}}\) (do E, F lần lượt là trung điểm của AA’, CC’) Suy ra \({V_{B.AEFC}} = \dfrac{1}{3}d\left( {B,\left( {AA'C'C} \right)} \right).{S_{ACFE}}\)\( = \dfrac{1}{3}d\left( {B,\left( {AA'C'C} \right)} \right).\dfrac{1}{2}{S_{AA'C'C}}\) \( = \dfrac{1}{2}.\dfrac{1}{3}d\left( {B,\left( {AA'C'C} \right)} \right).{S_{AA'C'C}}\)\( = \dfrac{1}{2}{V_{B.AA'C'C}} = \dfrac{1}{2}.\dfrac{2}{3}V = \dfrac{1}{3}V\) Suy ra \({V_{BEFA'B'C'}} = {V_{ABC.A'B'C'}} - {V_{B.ACFE}}\)\( = V - \dfrac{1}{3}V = \dfrac{2}{3}V\) Vậy tỉ số thể tích giữa hai phần là: \({V_{B.ACFE}}:{V_{BEFA'B'C'}} = \dfrac{1}{3}V:\dfrac{2}{3}V = 1:2\) Chọn C. Câu hỏi 49 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\), \(AB = a\). Gọi \(I\) là trung điểm của \(AC\), tam giác \(SAC\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp \(S.ABC\), biết góc giữa \(SB\) và mặt phẳng đáy bằng \({45^0}\).
Đáp án: A Phương pháp giải: - Chứng minh \(SI \bot \left( {ABC} \right)\). - Góc giữa \(SB\) và \(\left( {ABC} \right)\) là góc giữa \(SB\) và hình chiếu của \(SB\) lên \(\left( {ABC} \right)\). - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính chiều cao khối chóp. - Thể tích khối chóp có chiều cao \(h\), diện tích đáy \(B\) là \(V = \dfrac{1}{3}B.h\). Lời giải chi tiết:
Vì \(\Delta SAC\) cân tại \(S\) nên \(SI \bot AC\). Ta có: \(\left\{ \begin{array}{l}\left( {SAC} \right) \bot \left( {ABC} \right)\\\left( {SAC} \right) \cap \left( {ABC} \right) = AC\\\left( {SAC} \right) \supset SI \bot AC\end{array} \right.\) \( \Rightarrow SI \bot \left( {ABC} \right)\). \( \Rightarrow IB\) là hình chiếu của \(SB\) lên \(\left( {ABC} \right)\). \(\angle \left( {SB;\left( {ABC} \right)} \right) = \angle \left( {SB;IB} \right) = \angle SBI = {45^0}\). Tam giác \(ABC\) vuông cân tại \(B\), có \(AB = a\) nên \(BI = \dfrac{{a\sqrt 2 }}{2}\). Ta có \(SI \bot \left( {ABC} \right)\) nên \(SI \bot BI\), suy ra tam giác \(SIB\) vuông tại \(I\). Lại có \(\angle SBI = {45^0}\) nên \(\Delta SIB\) vuông cân tại \(I \Rightarrow SI = IB = \dfrac{{a\sqrt 2 }}{2}\). Ta có: \({S_{\Delta ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}{a^2}\). Vậy \({V_{S.ABC}} = \dfrac{1}{3}{S_{ABC}}.SI = \dfrac{1}{3}.\dfrac{{{a^2}}}{2}.\dfrac{{a\sqrt 2 }}{2} = \dfrac{{{a^3}\sqrt 2 }}{{12}}\). Chọn: A. Câu hỏi 50 : Khối chóp \(S.ABC\) có \(SA\) vuông góc với \(\left( {ABC} \right)\), đáy \(ABC\) là tam giác vuông tại B, biết \(SB = 2a\), \(BC = a\) và thể tích khối chóp là \({a^3}\). Khoảng cách từ \(A\) đến \(\left( {SBC} \right)\) là:
Đáp án: A Phương pháp giải: Sử dụng công thức tính khoảng cách dựa vào thể tích: \(d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{3{V_{S.ABC}}}}{{{S_{\Delta SBC}}}}\). Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right.\)\( \Rightarrow BC \bot \left( {SAB} \right).\) \( \Rightarrow BC \bot SB\)\( \Rightarrow {S_{SBC}} = \dfrac{1}{2}.SB.BC = \dfrac{1}{2}.2a.a = {a^2}.\) \(d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{3{V_{S.ABC}}}}{{{S_{\Delta SBC}}}} = \dfrac{{3{a^3}}}{{{a^2}}} = 3a.\) Chọn: A.
|