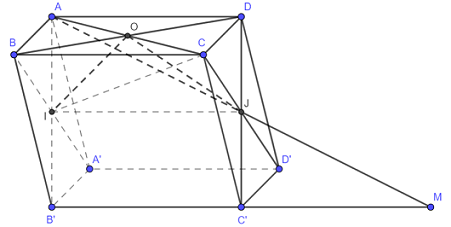
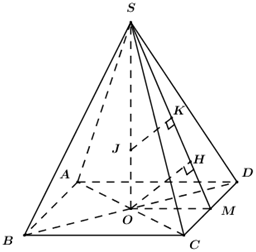
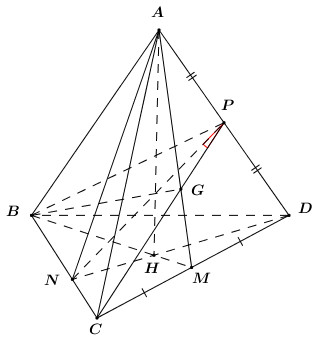
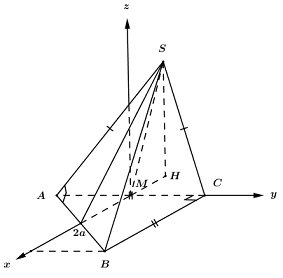
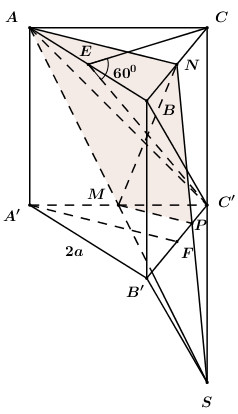
20 bài tập trắc nghiệm thể tích khối đa diện mức độ vận dụng caoLàm bàiCâu hỏi 1 : Cho hình hộp \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thoi tâm O và cạnh bằng a, \(\widehat {BAC} = {60^0}\). Gọi I, J lần lượt là tâm của các mặt bên \(ABB'A',\,CDD'C'\). Biết \(AI = \dfrac{{a\sqrt 7 }}{2},\,AA' = 2a\) và góc giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {A'B'C'D'} \right)\) bằng \({60^0}\). Tính theo a thể tích của khối tứ diện \(AOIJ\).
Đáp án: C Phương pháp giải: Lập tỉ lệ thể tích. Lời giải chi tiết:
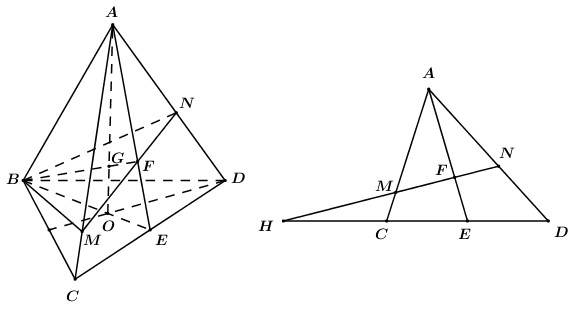
Lấy M đối xứng B’ qua C’\( \Rightarrow \) J là trung điểm của AM. Ta có: \({V_{AOIJ}} = \dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}.{V_{A.CB'M}} = \dfrac{1}{8}{V_{A.CB'M}}\) Mà \({S_{\Delta CB'M}} = {S_{BCC'B'}} \) \(\Rightarrow \)\({V_{A.CB'M}} = {V_{A.BCC'B'}} = \dfrac{1}{3}{V_{ABCD.A'B'C'D'}} \) \(\Rightarrow {V_{AOIJ}} = \dfrac{1}{{24}}{V_{ABCD.A'B'C'D'}}\) Ta có: \({S_{ABCD}} = 2.{S_{ABC}} = 2.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{2}\) Tam giác AA’B’ có: \(AB' = a\sqrt 7 ,\,A'B' = a,\,AA' = 2a\) \( \Rightarrow \cos \widehat {B'AA'} = \dfrac{{7{a^2} + 4{a^2} - {a^2}}}{{2.\sqrt 7 a.2a}} = \dfrac{5}{{2\sqrt 7 }}\) \( \Rightarrow \sin \widehat {B'AA'} = \sqrt {\dfrac{3}{{28}}} \) \( \Rightarrow {S_{AA'B'}} = \dfrac{1}{2}.AB'.AA'.\sin \widehat {B'AA'} = \dfrac{1}{2}.a\sqrt 7 .2a.\sqrt {\dfrac{3}{{28}}} = \dfrac{{{a^2}\sqrt 3 }}{2}\) Mặt khác \({S_{AA'B'}} = \dfrac{1}{2}.AH.A'B' \Rightarrow \dfrac{1}{2}.AH.a = \dfrac{{{a^2}\sqrt 3 }}{2} \Rightarrow AH = a\sqrt 3 \) (trong đó: AH là đường cao của tam giác AA’B’) Do góc giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {A'B'C'D'} \right)\) bằng \({60^0}\) nên \(d\left( {A;\left( {A'B'C'D'} \right)} \right) = AH.\sin {60^0} = a\sqrt 3 .\dfrac{{\sqrt 3 }}{2} = \dfrac{{3a}}{2}\) \( \Rightarrow {V_{ABCD.A'B'C'D'}} = \dfrac{{3a}}{2}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{3{a^3}\sqrt 3 }}{4} \) \( \Rightarrow {V_{AOIJ}} = \dfrac{1}{{24}}{V_{ABCD.A'B'C'D'}} = \dfrac{1}{{24}}.\dfrac{{3{a^3}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{32}}\) Chọn C. Câu hỏi 2 : Cho tứ diện \(ABCD\) có \(G\) là điểm thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Mặt phẳng thay đổi chứa \(BG\) và cắt \(AC,\,\,AD\) lần lượt tại \(M\) và \(N\). Giá trị nhỏ nhất của tỉ số \(\dfrac{{{V_{ABMN}}}}{{{V_{ABCD}}}}\) là
Đáp án: B Phương pháp giải: Lời giải chi tiết:
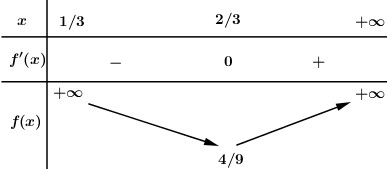
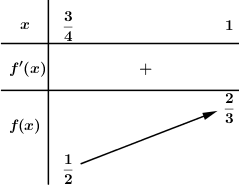
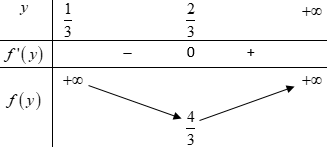
Gọi \(O\) là trọng tâm tam giác \(BCD\) \(\begin{array}{l} \Rightarrow \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = 3\overrightarrow {GO} \\ \Rightarrow \overrightarrow {GA} + 3\overrightarrow {GO} = \overrightarrow 0 \\ \Rightarrow \overrightarrow {GA} = - 3\overrightarrow {GO} \\ \Rightarrow \dfrac{{AG}}{{AO}} = \dfrac{3}{4}\end{array}\) Trong \(\left( {ABE} \right)\) gọi \(F = BG \cap AE\,\,\left( {F \in AE} \right)\). Lấy \(M \in AC\), trong \(\left( {ACD} \right)\) gọi \(N = MF \cap AD\,\,\,\left( {N \in AD} \right)\), khi đó ta có mặt phẳng chứa \(BG\) cắt \(AC,\,\,AD\) lần lượt tại \(M,\,\,N\) chính là \(\left( {BMN} \right)\). Áp dụng định lí Menelaus trong tam giác \(AOE\), cát tuyến \(BGF\): \(\dfrac{{GA}}{{GO}}.\dfrac{{BO}}{{BE}}.\dfrac{{FE}}{{FA}} = 1 \Rightarrow 3.\dfrac{2}{3}.\dfrac{{FE}}{{FA}} = 1 \Rightarrow \dfrac{{FE}}{{FA}} = \dfrac{1}{2}\) \( \Rightarrow \dfrac{{AF}}{{AE}} = \dfrac{2}{3}\) \( \Rightarrow F\) là trọng tâm tam giác \(ACD\). Trong \(\left( {ACD} \right)\) kéo dài \(MN\) cắt \(CD\) tại \(H\). Đặt \(\dfrac{{AM}}{{AC}} = x\) \(\left( {0 < x < 1} \right)\). Áp dụng định lí Menelaus trong tam giác \(ACE\), cát tuyến \(MHF\): \(\dfrac{{MA}}{{MC}}.\dfrac{{HC}}{{HE}}.\dfrac{{FE}}{{FA}} = 1 \Rightarrow \dfrac{x}{{1 - x}}.\dfrac{{HC}}{{HE}}.\dfrac{1}{2} = 1\)\( \Rightarrow \dfrac{{HC}}{{HE}} = \dfrac{{2\left( {1 - x} \right)}}{x}\) \(\begin{array}{l} \Rightarrow HE = \dfrac{x}{{2\left( {1 - x} \right)}}HC\\ \Rightarrow HC + CE = \dfrac{x}{{2\left( {1 - x} \right)}}HC\\ \Rightarrow CE = \dfrac{{3x - 2}}{{2\left( {1 - x} \right)}}HC\end{array}\) Ta có: \(\begin{array}{l}HD = HC + 2CE\\\,\,\,\,\,\,\,\,\, = HC + \dfrac{{3x - 2}}{{1 - x}}HC = \dfrac{{2x - 1}}{{1 - x}}HC\\ \Rightarrow \dfrac{{HE}}{{HD}} = \dfrac{x}{{2\left( {1 - x} \right)}}:\dfrac{{2x - 1}}{{1 - x}} = \dfrac{x}{{2\left( {2x - 1} \right)}}\end{array}\) Áp dụng định lí Menelaus trong tam giác \(AED\), cát tuyến \(MFN\): \(\begin{array}{l}\dfrac{{FA}}{{FE}}.\dfrac{{HE}}{{HD}}.\dfrac{{ND}}{{NA}} = 1 \Rightarrow 2.\dfrac{x}{{2\left( {2x - 1} \right)}}.\dfrac{{ND}}{{NA}} = 1\\ \Rightarrow \dfrac{{ND}}{{NA}} = \dfrac{{2x - 1}}{x} \Rightarrow \dfrac{{NA}}{{ND}} = \dfrac{x}{{2x - 1}}\\ \Rightarrow \dfrac{{NA}}{{NA + ND}} = \dfrac{x}{{x + 2x - 1}} = \dfrac{x}{{3x - 1}}\\ \Rightarrow \dfrac{{AN}}{{AD}} = \dfrac{x}{{3x - 1}}\end{array}\). Khi đó ta có \(\dfrac{{{V_{ABMN}}}}{{{V_{ABCD}}}} = \dfrac{{AM}}{{AC}}.\dfrac{{AN}}{{AD}} = x.\dfrac{x}{{3x - 1}} = \dfrac{{{x^2}}}{{3x - 1}}\,\,\left( {x > \dfrac{1}{3}} \right)\). Xét hàm số \(f\left( x \right) = \dfrac{{{x^2}}}{{3x - 1}}\,\,\left( {x > \dfrac{1}{3}} \right)\) ta có \(f'\left( x \right) = \dfrac{{2x\left( {3x - 1} \right) - 3{x^2}}}{{{{\left( {3x - 1} \right)}^2}}} = \dfrac{{3{x^2} - 2x}}{{{{\left( {3x - 1} \right)}^2}}}\); \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\left( {ktm} \right)\\x = \dfrac{2}{3}\end{array} \right.\) BBT:
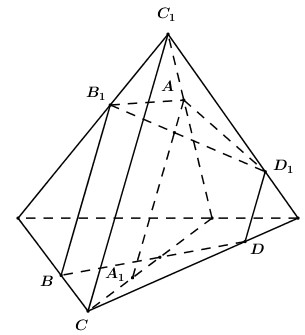
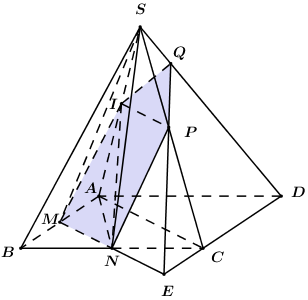
Dựa vào BBT ta thấy \(\mathop {\min }\limits_{\left( {\frac{1}{3}; + \infty } \right)} f\left( x \right) = f\left( {\dfrac{2}{3}} \right) = \dfrac{4}{9}\). Vậy giá trị nhỏ nhất của tỉ số \(\dfrac{{{V_{ABMN}}}}{{{V_{ABCD}}}} = \dfrac{4}{9}\). Chọn B. Câu hỏi 3 : Cho tứ diện \(ABCD\) có thể tích bằng \(18\). Gọi \({A_1}\) là trọng tâm của tam giác \(BCD\); \(\left( P \right)\) là mặt phẳng qua \(A\) sao cho góc giữa \(\left( P \right)\) và mặt phẳng \(\left( {BCD} \right)\) bằng \({60^0}\). Các đường thẳng qua \(B,\,\,C,\,\,D\) song song với \(A{A_1}\) cắt \(\left( P \right)\) lần lượt tại \({B_1},\,\,{C_1},\,\,{D_1}\). Thể tích khối tứ diện \({A_1}{B_1}{C_1}{D_1}\) bằng?
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Theo bài ra ta có \({A_1}\) là trọng tâm tam giác \(BCD\) nên \(A\) cũng là trọng tâm \(\Delta {B_1}{C_1}{D_1}\). Do đó \({V_{ABCD}} = 3{V_{A.{A_1}BC}} = 3{V_{B.A{A_1}C}}\) và \({V_{{A_1}{B_1}{C_1}{D_1}}} = 3{V_{{A_1}A{B_1}{C_1}}} = 3{V_{{B_1}A{A_1}{C_1}}}\). Mặt khác do quan hệ song song nên ta có: \(d\left( {B;\left( {A{A_1}C{C_1}} \right)} \right) = d\left( {B;\left( {A{A_1}C{C_1}} \right)} \right)\) và \({S_{\Delta A{A_1}C}} = {S_{\Delta A{A_1}{C_1}}}\) nên suy ra \({V_{B.A{A_1}C}} = {V_{{B_1}.A{A_1}{C_1}}}\) . Vậy \({V_{{A_1}{B_1}{C_1}{D_1}}} = {V_{ABCD}} = 18\). Chọn B. Câu hỏi 4 : Cho khối chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\) và có thể tích \(V = \dfrac{{{a^3}\sqrt 3 }}{6}\). Tìm số \(r > 0\) sao cho tồn tại điểm \(J\) nằm trong khối chóp mà khoảng cách từ \(J\) đến các mặt bên và mặt đáy đều bằng \(r\)?
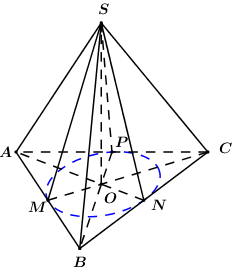
Đáp án: D Phương pháp giải: Lời giải chi tiết: Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\) . Vì khoảng cách từ \(J\) đến các mặt bên và mặt đáy đều bằng \(r\) nên \(J \in SO\). Gọi \(M\) là trung điểm của \(CD\), trong \(\left( {SOM} \right)\) kẻ \(OH \bot SM\) ta có: \(\begin{array}{l}\left\{ \begin{array}{l}CD \bot OM\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOM} \right) \Rightarrow CD \bot OH\\\left\{ \begin{array}{l}OH \bot CD\\OH \bot SM\end{array} \right. \Rightarrow OH \bot \left( {SCD} \right)\end{array}\) Trong \(\left( {SOM} \right)\) kẻ \(JK\parallel OH \Rightarrow JK \bot \left( {SCD} \right) \Rightarrow d\left( {J;\left( {SCD} \right)} \right) = JK\). Có \(d\left( {J;\left( {ABCD} \right)} \right) = JO\). Theo bài ra ta có \(JK = JO = r\). Ta có \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}\) \( \Rightarrow \dfrac{{{a^3}\sqrt 3 }}{6} = \dfrac{1}{3}SO.{a^2} \Rightarrow SO = \dfrac{{a\sqrt 3 }}{2}\). Áp dụng hệ thức lượng trong tam giác vuông ta có: \(OH = \dfrac{{SO.OM}}{{\sqrt {S{O^2} + O{M^2}} }} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}.\dfrac{a}{2}}}{{\sqrt {\dfrac{{3{a^2}}}{4} + \dfrac{{{a^2}}}{4}} }} = \dfrac{{a\sqrt 3 }}{4}\). Áp dụng định lí Ta-lét ta có \(\begin{array}{l}\dfrac{{JK}}{{OH}} = \dfrac{{SJ}}{{SO}} \Rightarrow \dfrac{r}{{\dfrac{{a\sqrt 3 }}{4}}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2} - r}}{{\dfrac{{a\sqrt 3 }}{2}}}\\ \Leftrightarrow 2r = \dfrac{{a\sqrt 3 }}{2} - r\\ \Leftrightarrow 3r = \dfrac{{a\sqrt 3 }}{2} \Leftrightarrow r = \dfrac{{a\sqrt 3 }}{6}\end{array}\) Chọn D. Câu hỏi 5 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,\,\,N\) lần lượt là trung điểm của các cạnh \(AB,\,\,BC\). Điểm \(I\) thuộc đoạn \(SA\). Biết mặt phẳng \(\left( {MNI} \right)\) chia khối chóp \(S.ABCD\) thành hai phần, phần chứa đỉnh \(S\) có thể tích bằng \(\dfrac{7}{{25}}\) lần phần còn lại. Tính tỉ số \(\dfrac{{IA}}{{IS}}\)?
Đáp án: A Phương pháp giải: - Xác đinh thiết diện của hình chóp cắt bởi \(\left( {IMN} \right)\). - Phân chia khối đa diện, cùng so sánh với \({V_{S.ABCD}}\). - Đặt \(\dfrac{{SI}}{{SA}} = x\,\,\left( {0 < x < 1} \right)\), so sánh thể tích phần chứa đỉnh \(S\) với \({V_{S.ABCD}}\), lập và giải phương trình tìm \(x\). Lời giải chi tiết: Giả sử \(SC \cap \left( {IMN} \right) = \left\{ P \right\}\) \( \Rightarrow \left( {IMN} \right) \cap \left( {SAC} \right) = IP\). Ta có: \(\left\{ \begin{array}{l}\left( {IMN} \right) \cap \left( {SAC} \right) = IP\\\left( {IMN} \right) \cap \left( {ABCD} \right) = MN\\\left( {SAC} \right) \cap \left( {ABCD} \right) = AC\end{array} \right. \Rightarrow IP\parallel MN\parallel AC\). Trong \(\left( {ABCD} \right)\) gọi \(\left\{ E \right\} = MN \cap CD\), trong \(\left( {SCD} \right)\) goji \(Q = NP \cap SD\). Khi đó thiết diện của hình chóp cắt bởi \(\left( {MNI} \right)\) là ngũ giác \(IMNPQ\). Gọi \({V_1} = {V_{S.BMNPQI}},\,\,V = {V_{S.ABCD}}\), theo bài ra ta có \({V_1} = \dfrac{7}{{32}}V\). Ta có \({V_1} = {V_{S.BMN}} + {V_{S.IMN}} + {V_{S.INP}} + {V_{S.IPQ}}\). Đặt \(\dfrac{{SI}}{{SA}} = x\,\,\,\left( {0 < x < 1} \right)\), áp dụng định lí Ta-lét ta có \(\dfrac{{SI}}{{SA}} = \dfrac{{SP}}{{SC}} = x\). - Xét khối chóp \(S.BMN\) và \(S.ABCD\): + Có cùng chiều cao (cùng bằng khoảng cách từ \(S\) đến \(\left( {ABCD} \right)\)). + \({S_{BMN}} = \dfrac{1}{4}{S_{ABC}} = \dfrac{1}{8}{S_{ABC}}\) (do tam giác \(BMN\) và tam giác \(BAC\) đồng dạng theo tỉ số \(\dfrac{1}{2}\)) Do đó \({V_{S.BMN}} = \dfrac{1}{8}{V_{S.ABCD}} = \dfrac{1}{8}V\). - Xét khối chóp \(S.IMN\) và \(S.AMN\): \(\dfrac{{{V_{S.IMN}}}}{{{V_{S.AMN}}}} = \dfrac{{SI}}{{SA}} = x \Rightarrow {V_{S.IMN}} = x.{V_{S.AMN}}\). Ta có \({S_{AMN}} = {S_{BMN}} = \dfrac{1}{8}{S_{ABCD}}\) \( \Rightarrow {V_{S.AMN}} = \dfrac{1}{8}V\) \( \Rightarrow {V_{S.IMN}} = \dfrac{x}{8}V\). - Xét khối chóp \(S.INP\) và \(S.ANC\): \(\dfrac{{{V_{S.INP}}}}{{{V_{S.ANC}}}} = \dfrac{{SI}}{{SA}}.\dfrac{{SP}}{{SC}} = {x^2} \Rightarrow {V_{S.IMN}} = {x^2}.{V_{S.ANC}}\). Ta có \({S_{ANC}} = \dfrac{1}{2}{S_{ABC}} = \dfrac{1}{4}{S_{ABCD}}\) \( \Rightarrow {V_{S.ANC}} = \dfrac{1}{4}V\) \( \Rightarrow {V_{S.IMN}} = \dfrac{{{x^2}}}{4}V\). - Xét khối chóp \(S.IPQ\) và \(S.ACD\): \(\dfrac{{{V_{S.IPQ}}}}{{{V_{S.ACD}}}} = \dfrac{{SI}}{{SA}}.\dfrac{{SP}}{{SC}}.\dfrac{{SQ}}{{SD}}\). Ta có \(AMEC\) là hình bình hành nên \(EC = AM = \dfrac{1}{2}CD \Rightarrow \dfrac{{EC}}{{ED}} = \dfrac{1}{3}\). Áp dụng định lí Menelaus trong tam giác \(SCD\) với cát tuyến \(EPQ\) ta có: \(\dfrac{{PS}}{{PC}}.\dfrac{{EC}}{{ED}}.\dfrac{{QD}}{{QS}} = 1\) \( \Rightarrow \dfrac{x}{{1 - x}}.\dfrac{1}{3}.\dfrac{{QD}}{{QS}} = 1\) \(\begin{array}{l} \Rightarrow \dfrac{{QD}}{{QS}} = \dfrac{{3\left( {1 - x} \right)}}{x} \Rightarrow \dfrac{{SQ}}{{QD}} = \dfrac{x}{{3\left( {1 - x} \right)}}\\ \Rightarrow \dfrac{{SQ}}{{SQ + QD}} = \dfrac{x}{{x + 3\left( {1 - x} \right)}}\\ \Rightarrow \dfrac{{SQ}}{{SD}} = \dfrac{x}{{3 - 2x}}\end{array}\) Suy ra \(\dfrac{{{V_{S.IPQ}}}}{{{V_{S.ACD}}}} = \dfrac{{SI}}{{SA}}.\dfrac{{SP}}{{SC}}.\dfrac{{SQ}}{{SD}} = {x^2}.\dfrac{x}{{3 - 2x}} = \dfrac{{{x^3}}}{{3 - 2x}}\)\( \Rightarrow {V_{S.IPQ}} = \dfrac{{{x^3}}}{{3 - 2x}}{V_{S.ACD}}\). Mà \({S_{ACD}} = \dfrac{1}{2}{S_{ABCD}} \Rightarrow {V_{S.ACD}} = \dfrac{1}{2}V\) \( \Rightarrow {V_{S.IPQ}} = \dfrac{{{x^3}}}{{2\left( {3 - 2x} \right)}}V\). Khi đó ta có: \(\begin{array}{l}\,\,\,\,\,\,{V_1} = {V_{S.BMN}} + {V_{S.IMN}} + {V_{S.INP}} + {V_{S.IPQ}}\\ \Rightarrow {V_1} = \dfrac{1}{8}V + \dfrac{x}{8}V + \dfrac{{{x^2}}}{4}V + \dfrac{{{x^3}}}{{2\left( {3 - 2x} \right)}}V\\ \Rightarrow {V_1} = \left( {\dfrac{1}{8} + \dfrac{x}{8} + \dfrac{{{x^2}}}{4} + \dfrac{{{x^3}}}{{2\left( {3 - 2x} \right)}}} \right)V = \dfrac{7}{{32}}V\\ \Rightarrow \dfrac{1}{8} + \dfrac{x}{8} + \dfrac{{{x^2}}}{4} + \dfrac{{{x^3}}}{{2\left( {3 - 2x} \right)}} = \dfrac{7}{{32}}\\ \Leftrightarrow \dfrac{{1 + x + 2{x^2}}}{4} + \dfrac{{{x^3}}}{{3 - 2x}} = \dfrac{7}{{16}}\\ \Leftrightarrow \left( {1 + x + 2{x^2}} \right).\left( {12 - 8x} \right) + 16{x^3} = 7\left( {3 - 2x} \right)\\ \Leftrightarrow 12 + 12x + 24{x^2} - 8x - 8{x^2} - 16{x^3} + 16{x^3} = 21 - 14x\\ \Leftrightarrow 16{x^2} + 18x - 9 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{3}{8}\,\,\,\,\,\,\,\left( {tm} \right)\\x = - \dfrac{3}{2}\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) \( \Rightarrow \dfrac{{SI}}{{SA}} = \dfrac{3}{8} \Rightarrow \dfrac{{IS}}{{IA}} = \dfrac{3}{5} \Rightarrow \dfrac{{IA}}{{IS}} = \dfrac{5}{3}\). Chọn A. Câu hỏi 6 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(\sqrt 6 \). Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng \(3\sqrt 2 \). Tính thể tích nhỏ nhất của khối chóp \(S.ABC\)
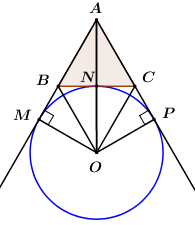
Đáp án: A Phương pháp giải: Lời giải chi tiết: Gọi \(M,\,\,N,\,\,P\) lần lượt là hình chiếu của điểm \(S\) lên \(AB,\,\,BC,\,\,AC\) ta có: \(\begin{array}{l}\,\,\,\,\,{S_{\Delta ABC}} = {S_{\Delta BCA}} = {S_{\Delta CAB}}\\ \Rightarrow \dfrac{1}{2}SM.AB = \dfrac{1}{2}SN.BC = \dfrac{1}{2}SP.CA\end{array}\) Mà \(AB = BC = CA\,\,\left( {gt} \right) \Rightarrow SM = SN = SP\). Gọi \(O\) là hình chiếu của \(S\) lên \(\left( {ABC} \right)\), ta có: \(\left\{ \begin{array}{l}AB \bot SM\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOM} \right) \Rightarrow AB \bot OM\). CMTT ta có \(ON \bot BC,\,\,OP \bot AC\). Xét các tam giác vuông \(\Delta SOM,\,\,\Delta SON,\,\,\Delta SOP\) có: \(\begin{array}{l}SO\,\,chung\\SM = SN = SP\,\,\left( {cmt} \right)\end{array}\) \( \Rightarrow \Delta SOM = \Delta SON = \Delta SOP\) (cạnh huyền – cạnh góc vuông) \( \Rightarrow OM = ON = OP\), suy ra \(O\) cách đều các cạnh \(AB,\,\,BC,\,\,CA\) nên \(O\) là tâm đường tròn nội tiếp \(\Delta ABC\) hoặc \(O\) là tâm đường tròn bàng tiếp \(\Delta ABC\). + TH1: \(O\) là tâm đường tròn nội tiếp \(\Delta ABC\). Mà \(\Delta ABC\) đều nên \(O\) là đồng thời là trọng tâm tam giác đều \(ABC\). Khi đó ta có \(AN = \dfrac{{\sqrt 6 .\sqrt 3 }}{2} = \dfrac{{3\sqrt 2 }}{2},\,\,AO = \dfrac{2}{3}AN = \sqrt 2 \). \( \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {18 - 2} = 4\). \({S_{\Delta ABC}} = {\left( {\sqrt 6 } \right)^2}.\dfrac{{\sqrt 3 }}{4} = \dfrac{{3\sqrt 3 }}{2}\). \( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SO.{S_{\Delta ABC}} = \dfrac{1}{3}.4.\dfrac{{3\sqrt 3 }}{2} = 2\sqrt 3 \). TH2: \(O\) là tâm đường tròn bàng tiếp \(\Delta ABC\). Gọi \(R\) là bán kính đường tròn bàng tiếp tam giác \(ABC\), \(p\) là nửa chu vi tam giác \(ABC\) \( \Rightarrow p = \dfrac{{3\sqrt 6 }}{2}\). Khi đó ta có \({S_{ABC}} = \left( {p - BC} \right).R\) \( \Rightarrow {\left( {\sqrt 6 } \right)^2}.\dfrac{{\sqrt 3 }}{4} = \left( {\dfrac{{3\sqrt 6 }}{2} - \sqrt 6 } \right).R \Leftrightarrow R = \dfrac{{3\sqrt 2 }}{2}\). Có \(AN = \dfrac{{\sqrt 6 .\sqrt 3 }}{2} = \dfrac{{3\sqrt 2 }}{2}\) \( \Rightarrow OA = AN + ON = 3\sqrt 2 \). \( \Rightarrow SA > OA = 3\sqrt 2 \) (quan hệ giữa đường vuông góc và đường xiên) \( \Rightarrow SB = 3\sqrt 2 \). Áp dụng định lí Pytago trong tam giác vuông \(OBM\) có: \(OB = \sqrt {O{M^2} + B{M^2}} = \sqrt {{{\left( {\dfrac{{3\sqrt 2 }}{2}} \right)}^2} + {{\left( {\dfrac{{\sqrt 6 }}{2}} \right)}^2}} = \sqrt 6 \). Áp dụng định lí Pytago trong tam giác vuông \(SOB\) có: \(SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {{{\left( {3\sqrt 2 } \right)}^2} - {{\left( {\sqrt 6 } \right)}^2}} = 2\sqrt 3 \). Khi đó ta có \({V_{S.ABC}} = \dfrac{1}{3}.SO.{S_{ABC}} = \dfrac{1}{3}.2\sqrt 3 .{\left( {\sqrt 6 } \right)^2}.\dfrac{{\sqrt 3 }}{4} = 3\). Vậy \(\min {V_{S.ABC}} = 3\). Chọn A. Câu hỏi 7 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, \(AD\) song song với \(BC\), \(AD = 2BC\). Gọi \(E\), \(F\) là hai điểm lần lượt nằm trên các cạnh \(AB\) và \(AD\) sao cho \(\dfrac{{3AB}}{{AE}} + \dfrac{{AD}}{{AF}} = 5\) (\(E,\,\,F\) không trùng với \(A\)), Tổng giá trị lớn nhất và giá trị nhỏ nhất của tỉ số thể tích hai khối chóp \(S.BCDFE\) và \(S.ABCD\) là:
Đáp án: D Phương pháp giải: Lời giải chi tiết:
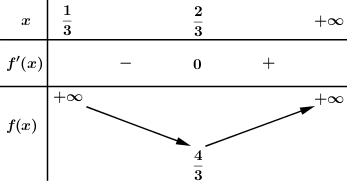
Đặt \(\dfrac{{AE}}{{AB}} = x,\,\,\dfrac{{AF}}{{AD}} = y\,\,\left( {0 < x,\,\,y \le 1} \right)\). Theo bài ra ta có: \(\dfrac{{3AB}}{{AE}} + \dfrac{{AD}}{{AF}} = 5\) \( \Rightarrow \dfrac{3}{x} + \dfrac{1}{y} = 5\,\,\,\left( 1 \right)\). Vì hai khối chóp \(S.BCDFE\) và \(S.ABCD\) có cùng chiều cao nên \(k = \dfrac{{{V_{S.BCDFE}}}}{{{V_{S.ABCD}}}} = \dfrac{{{S_{BCDFE}}}}{{{S_{ABCD}}}}\). Đặt \({S_{ABCD}} = S\), kẻ \(BH \bot AD\,\,\left( {H \in AD} \right)\) ta có \(S = \dfrac{1}{2}BH.\left( {BC + AD} \right) = \dfrac{3}{2}.BH.BC\). Ta có: \(\dfrac{{{S_{AEF}}}}{{{S_{ABD}}}} = \dfrac{{\dfrac{1}{2}AE.AF.\sin \angle BAD}}{{\dfrac{1}{2}AB.AD.\sin \angle BAD}} = xy \Rightarrow {S_{AEF}} = xy.{S_{ABD}}\). Mà \({S_{ABD}} = \dfrac{1}{2}BH.AD\) nên \({S_{AEF}} = \dfrac{1}{2}xy.BH.AD = xy.BH.BC = \dfrac{3}{2}BH.BC.\dfrac{2}{3}xy\) \( \Rightarrow {S_{AEF}} = \dfrac{2}{3}xy.S\). \( \Rightarrow {S_{BCDFE}} = {S_{ABCD}} - {S_{AEF}} = S - \dfrac{2}{3}xy.S = S\left( {1 - \dfrac{2}{3}xy} \right)\). \( \Rightarrow k = \dfrac{{S.\left( {1 - \dfrac{2}{3}xy} \right)}}{S} = 1 - \dfrac{2}{3}xy\). Theo (1) ta có: \(\dfrac{3}{x} + \dfrac{1}{y} = 5 \Leftrightarrow y = \dfrac{x}{{5x - 3}}\). Ta có \(0 < \dfrac{x}{{5x - 3}} \le 1 \Leftrightarrow \left\{ \begin{array}{l}\dfrac{x}{{5x - 3}} > 0\\\dfrac{{x - 5x + 3}}{{5x - 3}} \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x - 3 > 0\,\,\left( {do\,\,x > 0} \right)\\3 - 4x \le 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x > \dfrac{3}{5}\\x \ge \dfrac{3}{4}\end{array} \right. \Leftrightarrow x \ge \dfrac{3}{4}\). Khi đó ta có \(\begin{array}{l}k = 1 - \dfrac{2}{3}xy = 1 - \dfrac{2}{3}x.\dfrac{x}{{5x - 3}}\\\,\,\,\, = 1 - \dfrac{{2{x^2}}}{{3\left( {5x - 3} \right)}} = \dfrac{{15x - 9 - 2{x^2}}}{{3\left( {5x - 3} \right)}} = f\left( x \right)\end{array}\) Xét hàm số \(f\left( x \right) = \dfrac{{ - 2{x^2} + 15x - 9}}{{3\left( {5x - 3} \right)}}\) với \(\dfrac{3}{4} \le x \le 1\) ta có: \(\begin{array}{l}f'\left( x \right) = \dfrac{{\left( { - 4x + 15} \right).3\left( {5x - 3} \right) - \left( { - 2{x^2} + 15x - 9} \right).15}}{{9{{\left( {5x - 3} \right)}^2}}}\\f'\left( x \right) = \dfrac{{3\left( { - 20{x^2} + 87x - 45} \right) - \left( { - 30{x^2} + 225x - 135} \right)}}{{9{{\left( {5x - 3} \right)}^2}}}\\f'\left( x \right) = \dfrac{{ - 30{x^2} + 36x}}{{9{{\left( {5x - 3} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{6}{5}\,\,\left( {ktm} \right)\\x = 0\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) BBT:
\( \Rightarrow {k_{\min }} = \dfrac{1}{2},\,\,{k_{\max }} = \dfrac{2}{3}\). Vậy \({k_{\min }} + {k_{\max }} = \dfrac{1}{2} + \dfrac{2}{3} = \dfrac{7}{6}\). Chọn D. Câu hỏi 8 : Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh bằng \(2\), \(\angle BAD = {60^0}\), \(SA = SC\) và tam giác \(SBD\) vuông cân tại \(S\). Gọi \(E\) là trung điểm của \(SC\). Mặt phẳng \(\left( P \right)\) qua \(AE\) và cắt hai cạnh \(SB,\,\,SD\) lần lượt tại \(M\) và \(N\). Thể tích lớn nhất \({V_0}\) của khối đa diện \(ABCDNEM\) bằng:
Đáp án: D Phương pháp giải: - Đặt \(\dfrac{{SM}}{{SB}} = x,\,\,\dfrac{{SN}}{{SD}} = y\,\,\left( {0 < x,\,\,y < 1} \right)\). Tính \({V_{S.AMNE}}\) theo \({V_{S.ABCD}}\) theo 2 cách: \({V_{S.AMNE}} = {V_{S.AMN}} + {V_{S.MNE}}\), \({V_{S.AMNE}} = {V_{S.AME}} + {V_{S.ANE}}\) dựa vào công thức tỉ số thể tích. - Rút \(x\) theo \(y\) hoặc ngược lại. - Suy ra biểu thức tính tỉ số \(\dfrac{{{V_{S.AMNE}}}}{{{V_{S.ABCD}}}}\) theo \(x\) hoặc \(y\), sử dụng phương pháp hàm số để tìm GTNN. - Suy ra tỉ số lớn nhất của \(\dfrac{{{V_{ABCDNEM}}}}{{{V_{S.ABCD}}}}\). - Tính \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}\), với \(O = AC \cap BD\), sau đó suy ra \({V_0}\). Lời giải chi tiết:
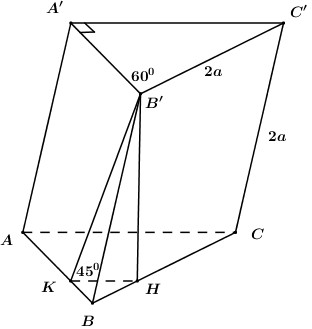
Gọi \(O = AC \cap BD\), ta có: \(SA = SC \Rightarrow \Delta SAC\) cân tại \(S\) \( \Rightarrow SO \bot AC\). Tam giác \(SBD\) vuông cân tại \(S\) \( \Rightarrow SO \bot BD\). \( \Rightarrow SO \bot \left( {ABCD} \right)\). Trong \(\left( {SBD} \right)\), gọi \(I = MN \cap BD\). Đặt \(\dfrac{{SM}}{{SB}} = x,\,\,\dfrac{{SN}}{{SD}} = y\,\,\left( {0 < x,\,\,y < 1} \right)\). Ta có: \(\dfrac{{{V_{S.AME}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SE}}{{SC}} = \dfrac{1}{2}x \Rightarrow \dfrac{{{V_{S.AME}}}}{{{V_{S.ABCD}}}} = \dfrac{1}{4}x\), \(\dfrac{{{V_{S.ANE}}}}{{{V_{S.ADC}}}} = \dfrac{{SN}}{{SD}}.\dfrac{{SE}}{{SC}} = \dfrac{1}{2}y \Rightarrow \dfrac{{{V_{S.ANE}}}}{{{V_{S.ABCD}}}} = \dfrac{1}{4}y\). \( \Rightarrow \dfrac{{{V_{S.AMNE}}}}{{{V_{S.ABCD}}}} = \dfrac{{{V_{S.AME}}}}{{{V_{S.ABCD}}}} + \dfrac{{{V_{S.ANE}}}}{{{V_{S.ABCD}}}} = \dfrac{{x + y}}{4}\,\,\,\left( 1 \right)\). Ta lại có: \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABD}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SD}} = xy \Rightarrow \dfrac{{{V_{S.AMN}}}}{{{V_{S.ABCD}}}} = \dfrac{{xy}}{2}\), \(\dfrac{{{V_{S.MNE}}}}{{{V_{S.BDC}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}}.\dfrac{{SE}}{{SC}} = \dfrac{1}{2}xy \Rightarrow \dfrac{{{V_{S.MNE}}}}{{{V_{S.ABCC}}}} = \dfrac{{xy}}{4}\). \( \Rightarrow \dfrac{{{V_{S.AMNE}}}}{{{V_{S.ABCD}}}} = \dfrac{{{V_{S.AMN}}}}{{{V_{S.ABCD}}}} + \dfrac{{{V_{S.MNE}}}}{{{V_{S.ABCD}}}} = \dfrac{{xy}}{2} + \dfrac{{xy}}{4} = \dfrac{{3xy}}{4}\,\,\left( 2 \right)\). Từ (1) và (2) \( \Rightarrow \dfrac{{x + y}}{4} = \dfrac{{3xy}}{4} \Leftrightarrow x + y = 3xy\)\( \Leftrightarrow x = \left( {3x - 1} \right)y \Leftrightarrow y = \dfrac{x}{{3x - 1}}\,\,\left( {x \ne \dfrac{1}{3}} \right)\). Do \(x,\,\,y > 0 \Rightarrow 3x - 1 > 0 \Leftrightarrow x > \dfrac{1}{3}\). Khi đó ta có \(\dfrac{{{V_{S.AMNE}}}}{{{V_{S.ABCD}}}} = \dfrac{1}{4}\left( {x + \dfrac{x}{{3x - 1}}} \right)\). Xét hàm số \(f\left( x \right) = x + \dfrac{x}{{3x - 1}}\,\,\left( {x > \dfrac{1}{3}} \right)\) ta có: \(f'\left( x \right) = 1 - \dfrac{1}{{{{\left( {3x - 1} \right)}^2}}} = 0\) \( \Leftrightarrow \left[ \begin{array}{l}3x - 1 = 1\\3x - 1 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{2}{3}\\x = 0\,\,\,\left( {ktm} \right)\end{array} \right.\) BBT:
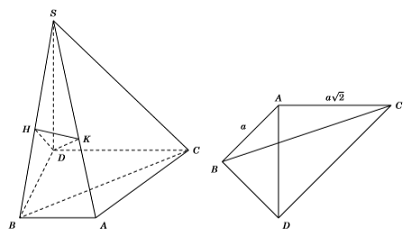
Dựa vào BBT ta thấy \(\min {V_{S.AMNE}} = \dfrac{1}{4}.\dfrac{4}{3}{V_{S.ABCD}} = \dfrac{1}{3}{V_{S.ABCD}}\) \( \Rightarrow \max {V_{ABCDNEM}} = \dfrac{2}{3}{V_{S.ABCD}} \Rightarrow {V_0} = \dfrac{2}{3}{V_{S.ABCD}}\). Ta có: \(\Delta ABD\) đều cạnh 2 \(\left( {AB = AD,\,\angle BAD = {{60}^0}} \right)\) \( \Rightarrow {S_{ABD}} = \dfrac{{{2^2}\sqrt 3 }}{4} = \sqrt 3 \) \( \Rightarrow {S_{ABCD}} = 2\sqrt 3 \). Tam giác \(ABD\) đều cạnh 2 \( \Rightarrow \)\(BD = 2\), lại có tam giác \(SBD\) vuông cân tại \(S\) nên \(SO = \dfrac{1}{2}BD = 1\). \( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.1.2\sqrt 3 = \dfrac{{2\sqrt 3 }}{3}\). Vậy \({V_0} = \dfrac{2}{3}{V_{S.ABCD}} = \dfrac{{4\sqrt 3 }}{9}\). Chọn D. Câu hỏi 9 : Cho tứ diện \(ABCD\)có \(AB = a\sqrt 6 ,\) tam giác \(ACD\) đều, hình chiếu vuông góc của \(A\) lên mặt phẳng \(\left( {BCD} \right)\) trùng với trực tâm \(H\) của tam giác \(BCD,\) mặt phẳng \(\left( {ADH} \right)\)tạo với mặt phẳng \(\left( {ACD} \right)\)một góc \({45^0}.\) Tính thể tích khối tứ diện \(ABCD.\)
Đáp án: C Phương pháp giải: Lời giải chi tiết:
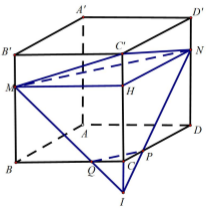
Gọi \(BM,\,\,DN\) lần lượt là các đường cao của tam giác \(BCD\) \( \Rightarrow BM \cap DN = \left\{ H \right\}\). Ta có: \(\left\{ \begin{array}{l}CD \bot BM\\CD \bot AH\end{array} \right. \Rightarrow CD \bot \left( {ABM} \right) \Rightarrow CD \bot AM\). \( \Rightarrow AM\) là đường cao của tam giác đều \(ACD\), do đó \(M\) là trung điểm của \(CD\). Gọi \(P\) là trung điểm của \(AD\), do \(\Delta ACD\) đều nên \(CP \bot AD\). Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AH\\BC \bot DN\end{array} \right. \Rightarrow BC \bot \left( {ADN} \right) \Rightarrow BC \bot AD\\\left\{ \begin{array}{l}AD \bot BC\\AD \bot CP\end{array} \right. \Rightarrow AD \bot \left( {BCP} \right) \Rightarrow AD \bot NP\end{array}\) Ta có: \(\left\{ \begin{array}{l}\left( {ADN} \right) \cap \left( {ACD} \right) = AD\\NP \subset \left( {ADN} \right),\,\,NP \bot AD\,\,\left( {cmt} \right)\\CP \subset \left( {ACD} \right),\,\,CP \bot AD\,\,\left( {cmt} \right)\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ADN} \right);\left( {ACD} \right)} \right) = \angle \left( {NP;CP} \right) = \angle NPC = {45^0}\). Ta có: \(BC \bot \left( {ADN} \right)\,\,\left( {cmt} \right) \Rightarrow CN \bot NP\) \( \Rightarrow NCP\) vuông tại \(N\), lại có \(\angle NPC = {45^0}\,\,\left( {cmt} \right)\) \( \Rightarrow \angle NCP = {45^0}\) hay \(\angle BCP = {45^0}\) (1). Gọi \(G = AM \cap CP \Rightarrow G\) là trọng tâm tam giác đều \(ACD\). Ta có: \(\left\{ \begin{array}{l}AD \bot \left( {BCP} \right)\,\,\left( {cmt} \right) \Rightarrow AD \bot BG\\CD \bot \left( {ABM} \right)\,\,\left( {cmt} \right) \Rightarrow CD \bot BG\end{array} \right.\) \( \Rightarrow BG \bot \left( {ACD} \right)\), mà \(G\) là trọng tâm tam giác đều \(ACD\) \( \Rightarrow BA = BC = BD = a\sqrt 6 \). Ta có \(BG \bot \left( {ACD} \right) \Rightarrow BG \bot CG\) \( \Rightarrow \Delta BCG\) vuông tại \(G\) (2). Từ (1) và (2) suy ra tam giác \(BCG\) vuông cân tại \(G\) \( \Rightarrow BG = CG = \dfrac{{BC}}{{\sqrt 2 }} = a\sqrt 3 \). Ta có: \(CP = \dfrac{3}{2}CG = \dfrac{{3a\sqrt 3 }}{2} = AC\dfrac{{\sqrt 3 }}{2}\) đều cạnh \(3a\) nên \({S_{\Delta ACD}} = \dfrac{{{{\left( {3a} \right)}^2}\sqrt 3 }}{4} = \dfrac{{9{a^2}\sqrt 3 }}{4}\). Vậy \({V_{ABCD}} = \dfrac{1}{3}BG.{S_{\Delta ACD}} = \dfrac{1}{3}.a\sqrt 3 .\dfrac{{9{a^2}\sqrt 3 }}{4} = \dfrac{{9{a^3}}}{4}\). Chọn C. Câu hỏi 10 : Cho hình lập phương \(ABCD.A'B'C'D'\) có thể tích \(V\). Gọi \(M\) là điểm thuộc cạnh \(BB'\) sao cho \(MB = 2MB'\). Mặt phẳng \(\left( \alpha \right)\) đi qua \(M\) và vuông góc với \(AC'\) cắt các cạnh \(DD'\), \(DC\), \(BC\) lần lượt tại \(N\), \(P\), \(Q\). Gọi \({V_1}\) là thể tích của khối đa diện \(CPQMNC'\).Tính tỉ số \(\dfrac{{{V_1}}}{V}\).
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Gọi cạnh của hình lập phương là \(a\). Ta có: \(\left( \alpha \right) \bot AC'\)\( \Rightarrow \left( \alpha \right)\parallel BD\). Trong \(\left( {BDD'B'} \right)\) kẻ \(MN\parallel BD\,\,\left( {N \in DD'} \right)\). \(\left( \alpha \right) \bot AC' \Rightarrow \alpha \parallel B'C\). Trong \(\left( {BCC'B'} \right)\) kẻ \(MQ\parallel B'C\,\,\left( {Q \in BC} \right)\). \(\left( \alpha \right) \bot AC'\)\( \Rightarrow \left( \alpha \right)\parallel BD\). Trong \(\left( {BDD'B'} \right)\) kẻ \(MN\parallel BD\,\,\left( {N \in DD'} \right)\). \(\left( \alpha \right) \bot AC' \Rightarrow \alpha \parallel B'C\). Trong \(\left( {ABCD} \right)\) kẻ \(PQ\parallel BD\,\,\left( {P \in DC} \right)\). Khi đó \(\left( \alpha \right) \equiv \left( {MNPQ} \right)\). Theo cách dựng ta có \(BQ = 2QC,\,\,DP = 2PC,\,\,DN = 2ND'\). Gọi \(H\) là điểm thuộc \(CC'\) sao cho \(CH = 2HC'\). Khi đó ta có: \({V_{CPQMNC'}} = {V_{C.MHN}} + {V_{CQP.MHN}}\). Xét hình chóp \(C'.MHN\) có \(C'H = \dfrac{a}{3}\), \({S_{\Delta MHN}} = \dfrac{1}{2}{a^2}\). \( \Rightarrow {V_{C'.MHN}} = \dfrac{1}{3}C'H.{S_{\Delta MHN}} = \dfrac{1}{3}.\dfrac{a}{3}.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}}}{{18}} = \dfrac{V}{{18}}\). Xét hình chóp cụt \(CQP.MHN\) có \(\begin{array}{l}{V_{CQP.MHN}} = {V_{I.MHN}} - {V_{I.CQP}} = \dfrac{1}{3}\left( {IH.{S_{\Delta MHN}} - IC.{S_{\Delta CQP}}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}\left( {a.\dfrac{1}{2}{a^2} - \dfrac{a}{3}.\dfrac{1}{2}.\dfrac{a}{3}.\dfrac{a}{3}} \right) = \dfrac{{13{a^3}}}{8} = \dfrac{{13V}}{{81}}\end{array}\) \( \Rightarrow {V_1} = {V_{CPQMNC'}} = {V_{C.MHN}} + {V_{CQP.MHN}} = \dfrac{V}{{18}} + \dfrac{{13V}}{{81}} = \dfrac{{35V}}{{162}}\). Vậy \(\dfrac{{{V_1}}}{V} = \dfrac{{35}}{{162}}\). Chọn B. Câu hỏi 11 : Khối chóp có đáy là hình bình hành, một cạnh đáy bằng \(a\) và các cạnh bên đều bằng \(a\sqrt 2 \). Thể tích của khối chóp có giá trị lớn nhất là:
Đáp án: D Phương pháp giải: - Gọi \(O = AC \cap BD\), chứng minh \(SO \bot \left( {ABCD} \right)\). - Chứng minh \(ABCD\) là hình chữ nhật. - Đặt \(AD = a,\,\,AB = x\), tính \(SO\) theo \(a\) và \(x\). - Tính thể tích khối chóp \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}\), sử dụng BĐT Cô-si: \(ab \le \dfrac{{{a^2} + {b^2}}}{2}\,\,\left( {a,\,\,b \ge 0} \right)\). Lời giải chi tiết:
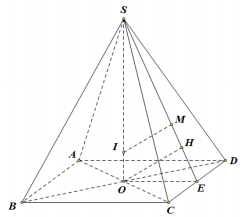
Gọi \(O = AC \cap BD\). Tam giác \(SAC\) cân tại \(S\), \(SO\) là trung tuyến \( \Rightarrow SO \bot AC\). Tam giác \(SBD\) cân tại \(S\), \(SO\) là trung tuyến \( \Rightarrow SO \bot BD\). \( \Rightarrow SO \bot \left( {ABCD} \right)\). Vì \(SA = SB = SC = SD\), \(SO \bot \left( {ABCD} \right)\) nên \(O\) là tâm đường tròn ngoại tiếp \(ABCD\). Hình bình hành \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) nên \(ABCD\) phải là hình chữ nhật. Theo bài ra ta giả sử \(AD = a\) và đặt \(AB = x\,\,\left( {x > 0} \right)\). Áp dụng định lí Pytago trong tam giác vuông \(ABC\) có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {x^2}} \). \( \Rightarrow AO = \dfrac{1}{2}AC = \dfrac{1}{2}\sqrt {{a^2} + {x^2}} \). Áp dụng định lí Pytago trong tam giác vuông \(SOA\) có: \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {2{a^2} - \dfrac{{{a^2} + {x^2}}}{4}} = \dfrac{1}{2}\sqrt {7{a^2} - {x^2}} \). Khi đó ta có \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{1}{2}\sqrt {7{a^2} - {x^2}} .ax = \dfrac{a}{6}x\sqrt {7{a^2} - {x^2}} \). Áp dụng BĐT Cô-si ta có: \(x\sqrt {7{a^2} - {x^2}} \le \dfrac{{{x^2} + 7{a^2} - {x^2}}}{2} = \dfrac{{7{a^2}}}{2}\) \( \Rightarrow {V_{S.ABCD}} \le \dfrac{a}{6}.\dfrac{{7{a^2}}}{2} = \dfrac{{7{a^3}}}{{12}}\). Dấu “=” xảy ra \( \Leftrightarrow {x^2} = 7{a^2} - {x^2} \Leftrightarrow x = \dfrac{{a\sqrt {14} }}{2}\). Vậy thể tích khối chóp \(S.ABCD\) đạt giá trị lớn nhất bằng \(\dfrac{{7{a^3}}}{{12}}\) \( \Leftrightarrow x = \dfrac{{a\sqrt {14} }}{2}\). Chọn D. Câu hỏi 12 : Cho hình chóp đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên bằng \(a\sqrt 2 \). Xét điểm \(M\) thay đổi trên mặt phẳng \(SCD\) sao cho tổng \(Q = M{A^2} + M{B^2} + M{C^2} + M{D^2} + M{S^2}\) nhỏ nhất. Gọi \({V_1}\) là thể tích của khối chóp \(S.ABCD\) và \({V_2}\) là thể tích của khối chóp \(M.ACD\). Tỉ số \(\dfrac{{{V_2}}}{{{V_1}}}\) bằng
Đáp án: C Phương pháp giải: - Gọi \(I\) là điểm thỏa mãn \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} + \overrightarrow {IS} = \overrightarrow 0 \), xác định vị trí điểm \(I\) và chứng minh \({Q_{\min }} \Leftrightarrow M{I_{\min }}\), khi đó \(M\) là hình chiếu của \(I\) lên \(\left( {SCD} \right)\) hay \(MI \bot \left( {SCD} \right)\). - Xác định tỉ số \(\dfrac{{d\left( {M;\left( {ABCD} \right)} \right)}}{{d\left( {S;\left( {ABCD} \right)} \right)}} = \dfrac{{ME}}{{SE}}\), sư dụng định lí Ta-lét và hệ thức lượng trong tam giác vuông để tính tỉ số. - Tính tỉ số thể tích bằng tỉ số chiều cao nhân tỉ số diện tích đáy. Lời giải chi tiết:
Gọi \(I\) là điểm thỏa mãn \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} + \overrightarrow {IS} = \overrightarrow 0 \). Ta có: \(\begin{array}{l}Q = M{A^2} + M{B^2} + M{C^2} + M{D^2} + M{S^2}\\Q = {\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {ID} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IS} } \right)^2}\\Q = 5M{I^2} + 2\overrightarrow {MI} \left( {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} + \overrightarrow {IS} } \right) + I{A^2} + I{B^2} + I{C^2} + I{D^2} + I{S^2}\\Q = 5M{I^2} + I{A^2} + I{B^2} + I{C^2} + I{D^2} + I{S^2}\end{array}\) Do các điểm \(I,\,\,A,\,\,B,\,\,C,\,\,D,\,\,S\) cố định nên \(I{A^2} + I{B^2} + I{C^2} + I{D^2} + I{S^2}\) không đổi, do đó \({Q_{\min }} \Leftrightarrow M{I_{\min }}\) Khi đó \(M\) là hình chiếu của \(I\) lên \(\left( {SCD} \right)\) hay \(MI \bot \left( {SCD} \right)\). Gọi \(O = AC \cap BD\) ta có \(SO \bot \left( {ABCD} \right)\) và: \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} + \overrightarrow {IS} = \overrightarrow 0 \)\( \Leftrightarrow \left( {\overrightarrow {IA} + \overrightarrow {IC} } \right) + \left( {\overrightarrow {IB} + \overrightarrow {ID} } \right) + \overrightarrow {IS} = \overrightarrow 0 \). \( \Leftrightarrow 2\overrightarrow {IO} + 2\overrightarrow {IO} + \overrightarrow {IS} = 0 \Leftrightarrow 4\overrightarrow {IO} = \overrightarrow {IS} \). Gọi \(E\) là trung điểm của \(CD\). Ta có: \(\left\{ \begin{array}{l}CD \bot OE\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOE} \right) \Rightarrow \left( {SOE} \right) \bot \left( {SCD} \right)\) \( \Rightarrow IM \subset \left( {SOE} \right)\). Trong \(\left( {SOE} \right)\) kẻ \(OH\parallel IM \Rightarrow OH \bot SE\). Ta có: \(\begin{array}{l}SE = \sqrt {S{C^2} - C{E^2}} = \sqrt {2{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 7 }}{2}\\SO = \sqrt {S{E^2} - O{E^2}} = \sqrt {\dfrac{{7{a^2}}}{4} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 6 }}{2}\\\dfrac{{SM}}{{SH}} = \dfrac{{SI}}{{SO}} = \dfrac{4}{5}\\\dfrac{{SH}}{{SE}} = \dfrac{{S{O^2}}}{{S{E^2}}} = \dfrac{{6{a^2}}}{4}:\dfrac{{7{a^2}}}{4} = \dfrac{6}{7}\\ \Rightarrow \dfrac{{SM}}{{SE}} = \dfrac{{SM}}{{SH}}.\dfrac{{SH}}{{SE}} = \dfrac{4}{5}.\dfrac{6}{7} = \dfrac{{24}}{{35}} \Rightarrow \dfrac{{ME}}{{SE}} = \dfrac{{11}}{{35}}\end{array}\) Ta có: \(SM \cap \left( {ABCD} \right) = E \Rightarrow \dfrac{{d\left( {M;\left( {ABCD} \right)} \right)}}{{d\left( {S;\left( {ABCD} \right)} \right)}} = \dfrac{{ME}}{{SE}} = \dfrac{{11}}{{35}}\). Vậy \(\dfrac{{{V_2}}}{{{V_1}}} = \dfrac{{{V_{M.ACD}}}}{{{V_{S.ABCD}}}} = \dfrac{{\dfrac{1}{3}.d\left( {M;\left( {ABCD} \right)} \right).{S_{ACD}}}}{{\dfrac{1}{3}.d\left( {S;\left( {ABCD} \right)} \right).{S_{ABCD}}}} = \dfrac{{11}}{{35}}.\dfrac{1}{2} = \dfrac{{11}}{{70}}\). Chọn C. Câu hỏi 13 : Cho hình chóp \(S.ABC\) có tam giác \(ABC\) vuông cân tại \(C\), tam giác \(SAB\) vuông tại \(A\), tam giác \(SAC\) cân tại \(S\). Biết \(AB = 2a\), đường thẳng \(SB\) tạo với mặt phẳng \(\left( {ABC} \right)\) góc \({45^0}\). Thể tích khối chóp \(S.ABC\) bằng:
Đáp án: D Phương pháp giải: Đặt hệ trục tọa độ. Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(AC\), \(N\) là trung điểm của \(AB\) ta có: \(\left\{ \begin{array}{l}AC \bot SM\\AC \bot MN\,\,\left( {MN\parallel AB} \right)\end{array} \right. \Rightarrow AC \bot \left( {SMN} \right)\). Trong \(\left( {SMN} \right)\) kẻ \(SH \bot MN\,\,\left( {H \in MN} \right)\), khi đó ta có: \(\left\{ \begin{array}{l}SH \bot MN\\SH \bot AC\end{array} \right. \Rightarrow SH \bot \left( {ABC} \right)\). Đặt hệ trục tọa độ như hình vẽ, coi \(a = 1\) ta có: \(M\left( {0;0;0} \right)\). Tam giác \(ABC\) vuông cân tại \(C\) nên \(AC = BC = \dfrac{{AB}}{{\sqrt 2 }} = a\sqrt 2 \) \( \Rightarrow AM = MC = \dfrac{{a\sqrt 2 }}{2}\). \( \Rightarrow A\left( {0; - \dfrac{{\sqrt 2 }}{2};0} \right),\,\,C\left( {0;\dfrac{{\sqrt 2 }}{2};0} \right)\), \(B\left( {\sqrt 2 ;\dfrac{{\sqrt 2 }}{2};0} \right)\). TH1: Đặt \(SH = x,\,\,HM = y\,\,\left( {x,\,\,y > 0} \right)\), khi đó ta có \(S\left( {y;0;x} \right)\), \(H\left( {y;0;0} \right)\). Ta có: \(\overrightarrow {SA} = \left( { - y; - \dfrac{{\sqrt 2 }}{2}; - x} \right),\,\,\overrightarrow {AB} = \left( {\sqrt 2 ;\sqrt 2 ;0} \right)\). Tam giác \(SAB\) vuông tại \(A\) \( \Rightarrow \overrightarrow {SA} .\overrightarrow {AB} = 0\). \( \Leftrightarrow - \sqrt 2 y - 1 = 0 \Leftrightarrow y = - \dfrac{1}{{\sqrt 2 }}\) (Vô lí), chứng tỏ điểm \(H\) nằm ngoài đoạn thẳng \(MN\) về phía điểm \(M\). TH2: Khi đó ta có \(HM = - y\,\,\left( {y > 0} \right)\) \( \Rightarrow S\left( { - y;0;x} \right),\,\,H\left( { - y;0;0} \right)\). Ta có: \(\overrightarrow {SA} = \left( {y; - \dfrac{{\sqrt 2 }}{2}; - x} \right),\,\,\overrightarrow {AB} = \left( {\sqrt 2 ;\sqrt 2 ;0} \right)\). Tam giác \(SAB\) vuông tại \(A\) \( \Rightarrow \overrightarrow {SA} .\overrightarrow {AB} = 0\) \( \Leftrightarrow \sqrt 2 y - 1 = 0 \Leftrightarrow y = \dfrac{1}{{\sqrt 2 }}\). Ta có \(SH \bot \left( {ABC} \right)\) nên \(HB\) là hình chiếu của \(SB\) lên \(\left( {ABC} \right)\). \( \Rightarrow \angle \left( {SB;\left( {ABC} \right)} \right) = \angle \left( {SB;HB} \right) = \angle SBH = {45^0}\). \( \Rightarrow \Delta SBH\) vuông cân tại \(H\) \( \Rightarrow SH = HB\) \(\begin{array}{l} \Rightarrow {x^2} = {\left( {y + \sqrt 2 } \right)^2} + {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^2} + {0^2}\\ \Leftrightarrow {x^2} = {\left( {\dfrac{1}{{\sqrt 2 }} + \sqrt 2 } \right)^2} + \dfrac{1}{2} = 5 \Leftrightarrow x = \sqrt 5 \\ \Rightarrow SH = a\sqrt 5 \end{array}\) \({S_{ABC}} = \dfrac{1}{2}AC.BC = \dfrac{1}{2}.{\left( {a\sqrt 2 } \right)^2} = {a^2}\). Vậy \({V_{S.ABC}} = \dfrac{1}{3}SH.{S_{ABC}} = \dfrac{1}{3}.a\sqrt 5 .{a^2} = \dfrac{{{a^3}\sqrt 5 }}{3}\). Chọn D. Câu hỏi 14 : Cho hình chóp \(S.ABC\), đáy là tam giác \(ABC\) có \(AB = BC\sqrt 5 \), \(AC = 2BC\sqrt 2 \), hình chiếu của \(S\) lên mặt phẳng \(\left( {ABC} \right)\) là trung điểm \(O\) của cạnh \(AC\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng 2. Mặt phẳng \(\left( {SBC} \right)\) hợp với mặt phẳng \(\left( {ABC} \right)\) một góc \(\alpha \) thay đổi. Biết rằng giá trị nhỏ nhất của thể tích khối chóp \(S.ABC\) bằng \(\dfrac{{\sqrt a }}{b}\), trong đó \(a,\,\,b \in {\mathbb{N}^*}\), \(a\) là số nguyên tố. Tổng \(a + b\) bằng:
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Gọi \(H\) là hình chiếu của \(O\) lên \(SB\). Ta có: \(OB = \sqrt {\dfrac{{2B{C^2} + 2B{A^2} - A{C^2}}}{4}} = BC\), \(OC = \dfrac{1}{2}AC = BC\sqrt 2 \). Suy ra \(OB \bot BC\). Dễ thấy \(\angle SBO = \alpha \) và \(OH = d\left( {O;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBC} \right)} \right) = 1\). Suy ra \(SO = \dfrac{{OH}}{{\cos \alpha }} = \dfrac{1}{{\cos \alpha }}\), \(OB = \dfrac{{OH}}{{\sin \alpha }} = \dfrac{1}{{\sin \alpha }}\). \( \Rightarrow BC = OB = \dfrac{1}{{\sin \alpha }}\). Thể tích khối chóp \(S.ABC\) là: \(\begin{array}{l}{V_{S.ABC}} = \dfrac{1}{3}SO.{S_{ABC}} = \dfrac{1}{3}SO.2{S_{OBC}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.\dfrac{1}{{\cos \alpha }}.{\left( {\dfrac{1}{{\sin \alpha }}} \right)^2} = \dfrac{1}{{3\cos \alpha .{{\sin }^2}\alpha }}\end{array}\) Áp dụng bất đẳng thức Cô-si ta có: \(\begin{array}{l}1 = \dfrac{1}{2}{\sin ^2}\alpha + \dfrac{1}{2}{\sin ^2}\alpha + {\cos ^2}\alpha \ge 3.\sqrt[3]{{\dfrac{1}{4}{{\sin }^4}\alpha .{{\cos }^2}\alpha }}\\ \Leftrightarrow \dfrac{1}{{27}} \ge \dfrac{1}{4}.si{n^4}\alpha .co{s^2}\alpha \Rightarrow \dfrac{1}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }} \ge \dfrac{{3\sqrt 3 }}{2}\\ \Rightarrow {V_{S.ABC}} \ge \dfrac{{\sqrt 3 }}{2}\end{array}\) Vậy \(\min {V_{S.ABC}} = \dfrac{{\sqrt 3 }}{2}\). Dấu “=” xảy ra \( \Leftrightarrow {\cos ^2}\alpha = \dfrac{1}{2}{\sin ^2}\alpha = \dfrac{1}{3} \Leftrightarrow \cos \alpha = \dfrac{{\sqrt 3 }}{3}\). \( \Rightarrow a = 3,\,\,b = 2\). Vậy \(a + b = 3 + 2 = 5\). Chọn B. Câu hỏi 15 : Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A.\) Cạnh \(BC = 2a\) và \(\angle ABC = {60^0}.\) Biết tứ giác \(BCC'B'\) là hình thoi có \(\angle B'BC\) nhọn. Mặt phẳng \(\left( {BCC'B'} \right)\) vuông góc với \(\left( {ABC} \right)\) và mặt phẳng \(\left( {ABB'A'} \right)\) tạo với \(\left( {ABC} \right)\) góc \({45^0}.\) Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Trong \(\left( {BCC'B'} \right)\) kẻ \(B'H \bot BC\,\,\left( {H \in BC} \right)\) (do \(\angle B'BC\) nhọn). Trong \(\left( {ABC} \right)\) kẻ \(HK\parallel AC \Rightarrow HK \bot AB\) ta có: \(\left\{ \begin{array}{l}AB \bot HK\\AB \bot B'H\end{array} \right. \Rightarrow AB \bot \left( {B'HK} \right) \Rightarrow AB \bot B'K\). Ta có: \(\left\{ \begin{array}{l}\left( {ABB'A'} \right) \cap \left( {ABC} \right) = AB\\B'K \subset \left( {ABB'A'} \right),\,\,B'K \bot AB\\HK \subset \left( {ABC} \right),\,\,HK \bot AB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ABB'A'} \right);\left( {ABC} \right)} \right) = \angle \left( {B'K;HK} \right) = \angle B'HK = {45^0}\). \( \Rightarrow \Delta B'HK\) vuông cân tại \(H \Rightarrow B'H = HK = x\). Xét tam giác vuông \(BB'H\) có: \(BH = \sqrt {BB{'^2} - BH{'^2}} = \sqrt {4{a^2} - {x^2}} \). Xét tam giác vuông \(ABC\) có: \(AC = BC.\sin {60^0} = a\sqrt 3 \), \(AB = BC.\cos {60^0} = a\). Áp dụng định lí Ta-lét ta có: \(\dfrac{{BH}}{{BC}} = \dfrac{{HK}}{{AC}} \Rightarrow \dfrac{{\sqrt {4{a^2} - {x^2}} }}{{2a}} = \dfrac{x}{{a\sqrt 3 }}\) \(\begin{array}{l} \Leftrightarrow 3\left( {4{a^2} - {x^2}} \right) = 4{x^2}\\ \Leftrightarrow 12{a^2} - 3{x^2} = 4{x^2}\\ \Leftrightarrow {x^2} = \dfrac{{12{a^2}}}{7}\\ \Leftrightarrow x = \dfrac{{2a\sqrt {21} }}{7} = B'H\end{array}\) \({S_{\Delta ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.a.a\sqrt 3 = \dfrac{{{a^2}\sqrt 3 }}{2}\). Vậy \({V_{ABC.A'B'C'}} = B'H.{S_{\Delta ABC}} = \dfrac{{2a\sqrt {21} }}{7}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{3{a^3}\sqrt 7 }}{7}\). Chọn B. Câu hỏi 16 : Cho hình chóp \(S.ABC\), đáy là tam giác \(ABC\) có \(AB = a\), \(AC = a\sqrt 2 \) và \(\angle CAB = {135^0}\), tam giác \(SAB\) vuông tại \(B\) và tam giác \(SAC\) vuông tại \(A\). Biết góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SAB} \right)\) bằng \({30^0}\). Tính thể tích khối chóp \(S.ABC\).
Đáp án: A Phương pháp giải: Lời giải chi tiết:
Gọi \(D\) là hình chiếu vuông góc của \(S\) lên mặt phẳng \(\left( {ABC} \right)\). Ta có: \(\left\{ \begin{array}{l}AB \bot SB\,\,\left( {gt} \right)\\AB \bot SD\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow AB \bot \left( {SBD} \right) \Rightarrow AB \bot BD\). \(\left\{ \begin{array}{l}AC \bot SA\,\,\left( {gt} \right)\\AC \bot SD\,\,\left( {SD \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow AC \bot \left( {SAD} \right) \Rightarrow AC \bot AD\). Ta có: \(\begin{array}{l}\angle BAC = \angle BAD + \angle DAC\\ \Rightarrow {135^0} = \angle BAD + {90^0}\\ \Rightarrow \angle BAD = {45^0}\end{array}\) \( \Rightarrow \Delta ABD\) vuông cân tại \(B\) \( \Rightarrow AD = AB\sqrt 2 = a\sqrt 2 = AC\). \( \Rightarrow \Delta ACD\) vuông cân tại \(A\). Ta có: \(\angle BDC = \angle BDA + \angle ADC = {45^0} + {45^0} = {90^0} = \angle ABD\) \( \Rightarrow ABDC\) là hình thang vuông tại \(B\) và \(D\). Trong \(\left( {SBD} \right)\) kẻ \(DH \bot SB\,\,\left( {H \in SB} \right)\) ta có: \(\left\{ \begin{array}{l}DH \bot SB\\DH \bot AB\,\,\left( {AB \bot \left( {SBD} \right)} \right)\end{array} \right. \Rightarrow DH \bot \left( {SAB} \right)\). Trong \(\left( {SAD} \right)\) kẻ \(DK \bot SA\,\,\left( {K \in SA} \right)\), ta có: \(\begin{array}{l}\left\{ \begin{array}{l}AC \bot AD\,\,\left( {cmt} \right)\\AC \bot SD\,\,\left( {SD \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow AC \bot \left( {SAD} \right) \Rightarrow AC \bot DK\\\left\{ \begin{array}{l}DK \bot SA\\DK \bot AC\end{array} \right. \Rightarrow DK \bot \left( {SAC} \right)\end{array}\). \( \Rightarrow \angle \left( {\left( {SAB} \right);\left( {SAC} \right)} \right) = \angle \left( {DH;DK} \right) = \angle HDK = {30^0}\) (do \(DH \bot \left( {SAB} \right) \Rightarrow DH \bot HK \Rightarrow \Delta DHK\) vuông tại \(H\)). Đặt \(SD = \,\,x > 0\). Áp dụng hệ thức lượng trong tam giác vuông ta có: \(\begin{array}{l}DH = \dfrac{{BD.SD}}{{\sqrt {B{D^2} + S{D^2}} }} = \dfrac{{ax}}{{\sqrt {{a^2} + {x^2}} }}\\DK = \dfrac{{AD.SD}}{{\sqrt {A{D^2} + S{D^2}} }} = \dfrac{{a\sqrt 2 .x}}{{\sqrt {2{a^2} + {x^2}} }} = \dfrac{{\sqrt 2 .ax}}{{\sqrt {2{a^2} + {x^2}} }}\end{array}\) Xét tam giác vuông \(DHK\) có: \(\begin{array}{l}\cos \angle HDK = \dfrac{{DH}}{{DK}}\\ \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{ax}}{{\sqrt {{a^2} + {x^2}} }}.\dfrac{{\sqrt {2{a^2} + {x^2}} }}{{\sqrt 2 .ax}}\\ \Leftrightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt {2{a^2} + {x^2}} }}{{\sqrt {2{a^2} + 2{x^2}} }}\\ \Leftrightarrow 6{a^2} + 6{x^2} = 8{a^2} + 4{x^2}\\ \Leftrightarrow 2{x^2} = 2{a^2} \Leftrightarrow x = a\end{array}\) Ta có \({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \angle BAC = \dfrac{1}{2}.a.a\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = \dfrac{{{a^2}}}{2}\). Vậy \({V_{S.ABC}} = \dfrac{1}{3}SD.{S_{\Delta ABC}} = \dfrac{1}{3}.a.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}}}{6}\). Chọn A. Câu hỏi 17 : Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(C\), \(AB = 2a\) và góc tạo bởi hai mặt phẳng \(\left( {ABC'} \right)\) và \(\left( {ABC} \right)\) bằng \({60^0}\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(A'C'\) và \(BC\). Mặt phẳng \(\left( {AMN} \right)\) chia khối lăng trụ thành hai phần. Thể tích của phần nhỏ bằng:
Đáp án: D Phương pháp giải: - Xác định thiết diện của lăng trụ khi cắt bởi \(\left( {AMN} \right)\). - Sử dụng định lí: Giao tuyến của ba mặt phẳng phân biệt hoặc đôi một song song, hoặc đồng quy. - Sử dụng tỉ lệ thể tích Simpson. - Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến. - Áp dụng công thức tính thể tích lăng trụ: \(V = Bh\) trong đó \(B,\,\,h\) lần lượt là chiều cao và diện tích đáy. Lời giải chi tiết:
Giả sử \(\left( {AMN} \right) \cap \left( {A'B'C'} \right) = MP\) ta có: \(\left\{ \begin{array}{l}\left( {AMN} \right) \cap \left( {ABC} \right) = AN\\\left( {AMN} \right) \cap \left( {A'B'C'} \right) = MP\\\left( {ABC} \right)\parallel \left( {A'B'C'} \right)\end{array} \right. \Rightarrow AN\parallel MP\). Khi đó \(\left( {AMN} \right) \equiv \left( {AMPN} \right)\) và thiết diện của lăng trụ cắt bởi \(\left( {AMN} \right)\) là tứ giác \(AMPN\). Và mặt phẳng này chia khối lăng trụ thành hai phần: \(ANC.MPC'\) và \(ABN.A'B'PM\). Ta lại có: \(\left\{ \begin{array}{l}\left( {AMPN} \right) \cap \left( {ACC'A'} \right) = AM\\\left( {AMPN} \right) \cap \left( {BCC'B'} \right) = PN\\\left( {ACC'A'} \right) \cap \left( {BCC'B'} \right) = CC'\end{array} \right.\) \( \Rightarrow AM,\,\,PN,\,\,CC'\) đồng quy tại \(S\). Gọi \(F\) là trung điểm của \(B'C'\) ta có \(A'F\parallel AN\parallel MP\), do đó \(MP\) là đường trung bình của tam giác \(A'C'F\) \( \Rightarrow \dfrac{{MP}}{{A'F}} = \dfrac{1}{2} = \dfrac{{MP}}{{AN}}\). Áp dụng định lí Ta-lét ta có: \(\dfrac{{MP}}{{AN}} = \dfrac{{SP}}{{SN}} = \dfrac{{SM}}{{SA}} = \dfrac{{SC'}}{{SC}} = \dfrac{1}{2}\). Khi đó ta có: \(\dfrac{{{V_{S.MPC'}}}}{{{V_{S.ANC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SP}}{{SN}}.\dfrac{{SC'}}{{SC}} = \dfrac{1}{8}\) \( \Rightarrow {V_{S.MNC'}} = \dfrac{1}{8}{V_{S.ANC}} \Rightarrow {V_{ANC.MPC'}} = \dfrac{7}{8}{V_{S.ANC}}\). Ta có: \({V_{S.ANC}} = \dfrac{1}{3}SC.{S_{ANC}} = \dfrac{1}{3}.2CC'.\dfrac{1}{2}{S_{\Delta ABC}} = \dfrac{1}{3}{V_{ABC.A'B'C'}}\). \( \Rightarrow {V_{ANC.MPC'}} = \dfrac{7}{{24}}{V_{ABC.A'B'C'}}\), do đó \(ANC.MPC'\) là phần có thể tích nhỏ hơn. Tam giác \(ABC\) vuông cân tại \(C\) có \(CE = \frac{1}{2}AB = a\), \(\angle CEC' = {60^0}\) \( \Rightarrow CC' = CE.\tan {60^0} = a\sqrt 3 \). \( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AC.BC = \dfrac{1}{2}.a\sqrt 2 .a\sqrt 2 = {a^2}\). Gọi \(E\) là trung điểm của \(AB\) ta có: \(CE \bot AB\) (do tam giác \(ABC\) vuông cân tại \(C\)). \( \Rightarrow \left\{ \begin{array}{l}AB \bot CE\\AB \bot CC'\end{array} \right. \Rightarrow AB \bot \left( {CC'E} \right) \Rightarrow AB \bot C'E\). \(\left\{ \begin{array}{l}\left( {ABC} \right) \cap \left( {ABC'} \right) = AB\\CE \subset \left( {ABC} \right),\,\,CE \bot AB\\C'E \subset \left( {ABC'} \right),\,\,C'E \bot AB\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {ABC} \right);\left( {ABC'} \right)} \right) = \angle \left( {CE;C'E} \right) = \angle CEC' = {60^0}\). Xét tam giác vuông \(CC'E\) có \(CE = \dfrac{1}{2}AB = a\), \(\angle CEC' = {60^0}\) \( \Rightarrow CC' = CE.\tan {60^0} = a\sqrt 3 \). \( \Rightarrow {V_{ABC.A'B'C'}} = CC'.{S_{\Delta ABC}} = a\sqrt 3 .{a^2} = {a^3}\sqrt 3 \). Vậy \({V_{ANC.MPC'}} = \dfrac{7}{{24}}{V_{ABC.A'B'C'}} = \dfrac{{7{a^3}\sqrt 3 }}{{24}}\). Chọn D. Câu hỏi 18 : Cho khối chóp S.ABCD có chiều cao bằng 9 và đáy là hình bình hành có diện tích bằng 10. Gọi M, N, P và Q lần lượt là trọng tâm các mặt bên SAB, SBC, SCD và SDA. Thể tích của khối đa diện lồi có đỉnh là các điểm M, N, P, Q, B và D bằng
Đáp án: B Phương pháp giải: - Xác định thiết diện \(A'B'C'D'\) của hình chóp cắt bởi mặt phẳng \(\left( {MNPQ} \right)\). - Phân chia khối đa diện: \(\begin{array}{l}{V_{MNPQBD}} = {V_{A'B'C'D'.ABCD}} - {V_{B.B'MN}} - {V_{D.D'PQ}} - {V_{A'MQ.ABD}} - {V_{C'NP.CBD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {V_{A'B'C'D'.ABCD}} - 2{V_{B.B'MN}} - 2{V_{A'MQ.ABD}}\end{array}\) - Sử dụng công thức tính thể tích chóp cụt: \(V = \dfrac{1}{3}\left( {S + S' + \sqrt {S.S'} } \right).h\) với \(S,\,\,S'\) là diện tích hai đáy, \(h\) là chiều cao của khối chóp cụt. Lời giải chi tiết:
Thiết diện của hình chóp cắt bởi \(\left( {MNPQ} \right)\) là tứ giác \(A'B'C'D'\) như hình vẽ. Khi đó ta có: \(\begin{array}{l}{V_{MNPQBD}} = {V_{A'B'C'D'.ABCD}} - {V_{B.B'MN}} - {V_{D.D'PQ}} - {V_{A'MQ.ABD}} - {V_{C'NP.CBD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {V_{A'B'C'D'.ABCD}} - 2{V_{B.B'MN}} - 2{V_{A'MQ.ABD}}\end{array}\) +) Ta có: Hình bình hành \(A'B'C'D'\) là \(ABCD\) đồng dạng theo tỉ số \(\dfrac{2}{3}\) nên \(\dfrac{{{S_{A'B'C'D'}}}}{{{S_{ABCD}}}} = {\left( {\dfrac{2}{3}} \right)^2} = \dfrac{4}{9}\) \( \Rightarrow {S_{A'B'C'D'}} = \dfrac{4}{9}{S_{ABCD}}\). Lại có: \(d\left( {S;\left( {A'B'C'D'} \right)} \right) = \dfrac{2}{3}d\left( {S;\left( {ABCD} \right)} \right)\). \(\begin{array}{l} \Rightarrow \dfrac{{{V_{S.A'B'C'D'}}}}{{{V_{S.ABCD}}}} = \dfrac{{\dfrac{1}{3}d\left( {S;\left( {A'B'C'D'} \right)} \right).{S_{A'B'C'D'}}}}{{\dfrac{1}{3}d\left( {S;\left( {ABCD} \right)} \right).{S_{ABCD}}}} = \dfrac{2}{3}.\dfrac{4}{9} = \dfrac{8}{{27}}\\ \Rightarrow {V_{S.A'B'C'D'}} = \dfrac{8}{{27}}{V_{S.ABCD}}\\ \Rightarrow {V_{A'B'C'D'.ABCD}} = \left( {1 - \dfrac{8}{{27}}} \right){V_{S.ABCD}} = \dfrac{{19}}{{27}}{V_{S.ABCD}}\end{array}\) +) Ta có \(BS \cap \left( {A'B'C'D'} \right) = B'\) \(\begin{array}{l} \Rightarrow \dfrac{{d\left( {B;\left( {A'B'C'D'} \right)} \right)}}{{d\left( {S;\left( {A'B'C'D'} \right)} \right)}} = \dfrac{{BB'}}{{SB'}} = \dfrac{1}{2}\\ \Rightarrow d\left( {B;\left( {A'B'C'D'} \right)} \right) = \dfrac{1}{2}d\left( {S;\left( {A'B'C'D'} \right)} \right)\\ \Rightarrow d\left( {B;\left( {A'B'C'D'} \right)} \right) = \dfrac{1}{2}.\dfrac{2}{3}d\left( {S;\left( {ABCD} \right)} \right)\\ \Rightarrow d\left( {B;\left( {A'B'C'D'} \right)} \right) = \dfrac{1}{3}d\left( {S;\left( {ABCD} \right)} \right)\end{array}\) Lại có: \({S_{B'MN}} = \dfrac{1}{4}{S_{A'B'C'}} = \dfrac{1}{8}{S_{A'B'C'D'}} = \dfrac{1}{8}.\dfrac{4}{9}{S_{ABCD}} = \dfrac{1}{{18}}{S_{ABCD}}\) \( \Rightarrow {V_{B.B'MN}} = \dfrac{1}{3}.\dfrac{1}{{18}} = \dfrac{1}{{54}}{V_{S.ABCD}}\). +) \({S_{C'NP}} = {S_{B'MN}} = \dfrac{1}{{18}}{S_{ABCD}}\); \({S_{BCD}} = \dfrac{1}{2}{S_{ABCD}}\), \(d\left( {\left( {A'B'C'D'} \right);\left( {ABCD} \right)} \right) = d\left( {B;\left( {A'B'C'D'} \right)} \right) = \dfrac{1}{3}d\left( {S;\left( {ABCD} \right)} \right)\). \(\begin{array}{l} \Rightarrow {V_{C'NP.CBD}} = \left( {\dfrac{1}{{18}}{S_{ABCD}} + \dfrac{1}{2}{S_{ABCD}} + \sqrt {\dfrac{1}{{18}}.\dfrac{1}{2}} {S_{ABCD}}} \right).\dfrac{1}{3}d\left( {S;\left( {ABCD} \right)} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{13}}{{54}}{S_{ABCD}}.d\left( {S;\left( {ABCD} \right)} \right) = \dfrac{{13}}{{54}}{V_{S.ABCD}}\end{array}\) \( \Rightarrow \) \({V_{MNPQBD}} = \left( {\dfrac{{19}}{{27}} - 2.\dfrac{1}{{54}} - 2.\dfrac{{13}}{{54}}} \right){V_{S.ABCD}} = \dfrac{5}{{27}}{V_{S.ABCD}}\). Mà \({V_{S.ABCD}} = \dfrac{1}{3}.9.10 = 30\). Vậy \({V_{MNPQBD}} = \dfrac{5}{{27}}.30 = \dfrac{{50}}{9}\). Chọn B. Câu hỏi 19 : Cho khối lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng \(a\) và góc giữa hai đường thẳng \(AB'\) và \(BC'\) bằng \({60^0}\). Thể tích khối lăng trụ đã cho bằng:
Đáp án: C Phương pháp giải: Lời giải chi tiết:
Gọi \(N = AB' \cap A'B\) và \(M\) là trung điểm của \(A'C'\). Ta có: \(MN\) là đường trung bình của tam giác \(A'C'B\) \( \Rightarrow MN\parallel BC'\) \( \Rightarrow \angle \left( {AB';BC'} \right) = \angle \left( {AB';MN} \right)\). \( \Rightarrow \angle \left( {AB';MN} \right) = {60^0}\) \( \Rightarrow \angle B'NM = {60^0}\) hoặc \(\angle B'NM = {120^0}\). Vì \(MN\) là đường trung bình của tam giác \(A'C'B\) nên \(MN = \dfrac{1}{2}BC'\). Hình chữ nhật \(BCC'B'\) và hình chữ nhật \(ABB'A'\) là hai hình chữ nhật bằng nhau nên \(BC' = AB'\) \( \Rightarrow MN = NB'\). TH1: \(\angle B'NM = {60^0}\), khi đó \(\Delta B'MN\) đều. Tam giác \(A'B'C'\) đều cạnh \(a \Rightarrow B'M = \dfrac{{a\sqrt 3 }}{2}\)\( = B'N = MN\). \( \Rightarrow AB' = 2B'N = a\sqrt 3 \). Áp dụng định lí Pytago trong tam giác vuông \(AA'B'\) ta có: \(AA' = \sqrt {AB{'^2} - A'B{'^2}} = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 \). \( \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}} = a\sqrt 2 .\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 6 }}{4}\). TH2: \(\angle B'NM = {120^0}\). Tam giác \(A'B'C'\) đều cạnh \(a \Rightarrow B'M = \dfrac{{a\sqrt 3 }}{2}\). Áp dụng định lí Cosin trong tam giác \(B'MN\) ta có: \(\begin{array}{l}\cos {120^0} = \dfrac{{B'{N^2} + M{N^2} - B'{M^2}}}{{2B'N.MN}}\\ \Leftrightarrow - \dfrac{1}{2} = \dfrac{{2M{N^2} - {{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}}}{{2M{N^2}}}\\ \Leftrightarrow - M{N^2} = 2M{N^2} - \dfrac{{3{a^2}}}{4}\\ \Leftrightarrow 3M{N^2} = \dfrac{{3{a^2}}}{4}\\ \Leftrightarrow MN = \dfrac{a}{2} = B'N\end{array}\) \( \Rightarrow AB' = 2B'N = a = AB\) (Vô lí do cạnh huyền không thể bằng cạnh góc vuông). Vậy \({V_{ABC.A'B'C'}} = \dfrac{{{a^3}\sqrt 6 }}{4}\). Chọn C. Câu hỏi 20 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích là V. Gọi P là trung điểm của SC. Mặt phẳng \(\left( \alpha \right)\) chứa AP và cắt SD, SB lần lượt tại M và N. Gọi V’ là thể tích của khối chóp S.AMPN. Tìm giá trị nhỏ nhất của tỉ số \(\dfrac{{V'}}{V}\).
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Đặt \(\dfrac{{SN}}{{SB}} = x,\,\,\dfrac{{SM}}{{SD}} = y\). Ta có: \(\dfrac{{{V_{S.ANP}}}}{{{V_{S.ABC}}}} = \dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}} = \dfrac{1}{2}x\) \( \Rightarrow {V_{S.ANP}} = \dfrac{x}{2}{V_{S.ABC}} = \dfrac{x}{4}V\). \(\dfrac{{{V_{S.APM}}}}{{{V_{S.ACD}}}} = \dfrac{{SP}}{{SC}}.\dfrac{{SM}}{{SD}} = \dfrac{1}{2}y\) \( \Rightarrow {V_{S.APM}} = \dfrac{y}{2}{V_{S.ACD}} = \dfrac{y}{4}V\). \( \Rightarrow {V_{S.AMNP}} = {V_{S.ANP}} + {V_{S.APM}} = \left( {\dfrac{x}{4} + \dfrac{y}{4}} \right)V\). Tương tự ta có: \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABD}}}} = \dfrac{{SN}}{{SB}}.\dfrac{{SM}}{{SD}} = xy\) \( \Rightarrow {V_{S.AMN}} = xy{V_{S.ABD}} = \dfrac{{xy}}{2}V\). \(\dfrac{{{V_{S.NPM}}}}{{{V_{S.BCD}}}} = \dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}}.\dfrac{{SM}}{{SD}} = \dfrac{1}{2}xy\) \( \Rightarrow {V_{S.NPM}} = \dfrac{1}{2}xy{V_{S.BCD}} = \dfrac{{xy}}{4}V\). \( \Rightarrow {V_{S.AMNP}} = {V_{S.AMN}} + {V_{S.NPM}} = \left( {\dfrac{{xy}}{2} + \dfrac{{xy}}{4}} \right)V = \dfrac{{3xy}}{4}V\). Khi đó ta có: \(\dfrac{x}{4} + \dfrac{y}{4} = \dfrac{{3xy}}{4} \Leftrightarrow x + y = 3xy\) \( \Leftrightarrow x\left( {3y - 1} \right) = y\). Do \(x,\,\,y > 0\) nên \(3y - 1 > 0 \Leftrightarrow y > \dfrac{1}{3}\), khi đó ta có \(x = \dfrac{y}{{3y - 1}}\,\,\left( {y > \dfrac{1}{3}} \right)\). Ta có \(\dfrac{{V'}}{V} = \dfrac{{x + y}}{4} = \dfrac{1}{4}\left( {\dfrac{y}{{3y - 1}} + y} \right) = \dfrac{1}{4}.\dfrac{{3{y^2}}}{{3y - 1}}\,\,\left( {y > \dfrac{1}{3}} \right)\). Xét hàm số \(f\left( y \right) = \dfrac{{3{y^2}}}{{3y - 1}}\) ta có \(\begin{array}{l}f'\left( y \right) = \dfrac{{6y\left( {3y - 1} \right) - 3{y^2}.3}}{{{{\left( {3y - 1} \right)}^2}}}\\f'\left( y \right) = \dfrac{{9{y^2} - 6y}}{{{{\left( {3y - 1} \right)}^2}}}\\f'\left( y \right) = 0 \Leftrightarrow \left[ \begin{array}{l}y = 0\\y = \dfrac{2}{3}\end{array} \right.\end{array}\) BBT:
Từ BBT ta thấy \(f\left( y \right)\) đạt GTNN bằng \(\dfrac{4}{3}\) tại \(y = \dfrac{2}{3}\). Vậy \(\min \dfrac{{V'}}{V} = \dfrac{1}{4}.\dfrac{4}{3} = \dfrac{1}{3}\). Chọn B.
|