Đề tham khảo thi THPT môn Toán - Đề số 1 (hay, chi tiết)I. Phần trắc nghiệmĐề bài
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Nguyên hàm của hàm số \(y = {2^x}\) là
Câu 3 :
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
Câu 4 :
Trong không gian Oxyz, đường thẳng \(d:\left\{ \begin{array}{l}x = 2 - t\\y = 1 + 2t\\z = 3 + t\end{array} \right.\) có một vecto chỉ phương là
Câu 5 :
Cho hàm số y = f(x) có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình
Câu 6 :
Tập nghiệm của bất phương trình \(\log x \ge 1\) là
Câu 7 :
Trong không gian Oxyz, cho mặt cầu (S): \({(x - 2)^2} + {(y + 1)^2} + {(z - 3)^2} = 4\). Tâm của (S) có tọa độ là
Câu 8 :
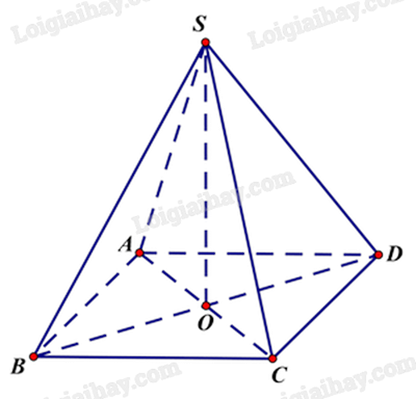
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA = SB = SC = SD. Khẳng định nào sau đây đúng?
Câu 9 :
Tập nghiệm của bất phương trình \({2^x} \le 4\) là
Câu 10 :
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3\) và công bội q = 2. Giá trị của \({u_2}\) bằng
Câu 11 :
Cho hình lập phương ABCD. A’B’C’D’. Mệnh đề nào sau đây sai?
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Cho phương trình lượng giác \(\sin 2x = - \frac{1}{2}\) (*). a) Phương trình (*) tương đương \(\sin 2x = \sin \left( { - \frac{\pi }{6}} \right)\).
Đúng
Sai
b) Trong khoảng \((0;\pi )\) phương trình (*) có 3 nghiệm.
Đúng
Sai
c) Tổng các nghiệm của phương trình (*) trong khoảng \((0;\pi )\) bằng \(\frac{{3\pi }}{2}\).
Đúng
Sai
d) Trong khoảng \((0;\pi )\) phương trình (*) có nghiệm lớn nhất bằng \(\frac{{7\pi }}{{12}}\).
Đúng
Sai
Câu 2 :
Một ô tô bắt đầu chuyển động nhanh dần đều với tốc độ v(t) = 5t (m/s), trong đó t là thời gian tính bằng giây kể từ khi ô tô bắt đầu chuyển động. Đi được 6 (s) người lái xe phát hiện chương ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc a = −5 \((m/{s^2})\). a) Tốc độ của ô tô tại thời điểm 10 giây tính từ lúc xuất phát là 10 (m/s).
Đúng
Sai
b) Quãng đường ô tô chuyển động được trong 6 giây đầu tiên là 80 m.
Đúng
Sai
c) Quãng đường S (đơn vị: mét) mà ô tô chuyển động được kể từ lúc bắt đầu đạp phanh đến khi dừng lại được tính theo công thức \(S = \int\limits_0^6 {(30 - 5t)dt} \).
Đúng
Sai
d) Quãng đường ô tô chuyển động được kể từ lúc bắt đầu chuyển động cho đến khi dừng lại là 170 m.
Đúng
Sai
Câu 3 :
Lớp 12A có 30 học sinh, trong đó có 17 bạn nữ còn lại là nam. Có 3 bạn tên Hiền, trong đó có 1 bạn nữ và 2 bạn nam. Thầy giáo gọi ngẫu nhiên một bạn lên bảng. a) Xác suất học sinh được gọi tên Hiền là \(\frac{1}{{10}}\).
Đúng
Sai
b) Xác suất học sinh được gọi tên Hiền, biết học sinh đó là nữ là \(\frac{3}{{17}}\).
Đúng
Sai
c) Xác suất học sinh được gọi tên Hiền, biết học sinh đó là nam là \(\frac{2}{{13}}\).
Đúng
Sai
d) Nếu thầy giáo gọi một bạn tên Hiền lên bảng thì xác suất bạn đó là nam là \(\frac{3}{{17}}\).
Đúng
Sai
Câu 4 :
Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm A(10;3;0) và chuyển động đều theo đường cáp có vectơ chỉ phương \(\overrightarrow u = (2; - 2;1)\), hướng chuyển động cùng chiều với hướng vectơ \(\overrightarrow u \) với tốc độ là 4,5 (m/s) (đơn vị trên mỗi trục là mét). a) Phương trình tham số của đường cáp là \(\left\{ \begin{array}{l}x = 10 + 2t\\y = 3 - 2t\\z = t\end{array} \right.\) \((t \in \mathbb{R})\).
Đúng
Sai
b) Giả sử sau thời gian t (giây) kể từ khi xuất phát \((t \ge 0)\), cabin đến điểm M. Khi đó, tọa độ điểm M là \(\left( {3t + 10; - 3t + 3;\frac{{3t}}{2}} \right)\).
Đúng
Sai
c) Cabin dừng ở điểm B có hoành độ \({x_B} = 550\), khi đó quãng đường AB dài 800 m.
Đúng
Sai
d) Đường cáp AB tạo với mặt phẳng (Oxy) một góc \({30^o}\).
Đúng
Sai
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng 2, cạnh bên bằng \(2\sqrt 2 \). Tính khoảng cách giữa hai đường thẳng AB và SD (kết quả làm tròn đến hàng phần mười). Đáp án:
Câu 2 :
Một người đưa thư xuất phát từ vị trí A, các điểm cần phát thư nằm dọc con đường đi qua. Biết rằng người này phải đi trên mỗi con đường ít nhất một lần (để phát được thư cho tất cả các điểm cần phát nằm dọc theo con đường đó) và cuối cùng quay lại điểm xuất phát. Độ dài các con đường như hình vẽ (đơn vị độ dài). Hỏi tổng quãng đường người đưa thư có thể đi ngắn nhất có thể là bao nhiêu?
Đáp án:
Câu 3 :
Khi gắn hệ tọa độ Oxyz (đơn vị trên mỗi trục tính theo kilomet) vào một sân bay, mặt phẳng Oxy trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí A(5;0;5) đến vị trí B(10;10;3) và hạ cánh tại vị trí M(a;b;0). Giá trị của a + b bằng bao nhiêu (viết kết quả dưới dạng số thập phân)? Đáp án:
Câu 4 :
Một bể chứa nhiên liệu hình trị đặt nằm ngang, có chiều dài 5 m, bán kính đáy 1 m. Chiều cao của mực nhiên liệu là 1,5 m. Tính thể tích phần nhiên liệu trong bể (theo đơn vị \({m^3}\), làm tròn đến hàng phần chục).
Đáp án:
Câu 5 :
Nhà máy A chuyển sản xuất một loại sản phẩm cho nhà máy B. Hai nhà máy thỏa thuận rằng, hằng tháng A cung cấp cho B số lượng sản phẩm theo đơn đặt hàng của B (tối đa 100 tấn sản phẩm). Nếu số lượng đặt hàng là x tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là \(P(x) = 45 - 0,001{x^2}\) (triệu đồng). Chi phí để A sản xuất x tấn sản phẩm trong một tháng là \(C(x) = 100 + 30x\) triệu đồng (gồm 100 triệu đồng chi phí cố định và 30 triệu đồng cho mỗi tấn sản phẩm). Nhà máy A bán cho B bao nhiêu tấn sản phẩm để lợi nhuận thu được là lớn nhất (làm tròn kết quả đến hàng phần mười)? Đáp án:
Câu 6 :
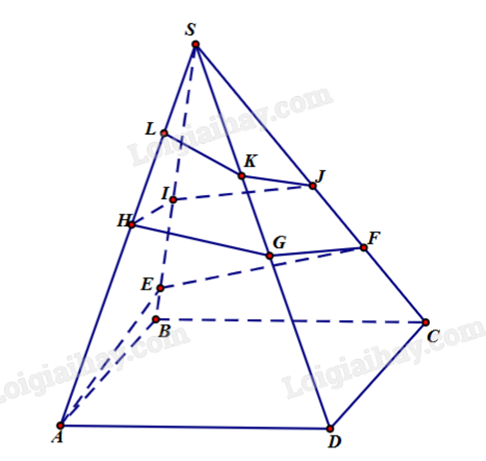
Người ta cần trang trí một kim tự tháp hình chóp tứ giác đều S.ABCD cạnh bên bằng 200 m, góc \(\widehat {ASB} = {15^o}\) bằng đường gấp khúc dây đèn led vòng quanh kim tự tháp AEFGHIJKLS. Trong đó, điểm L cố định và LS = 40 m. Hỏi, khi đó cần dùng ít nhất bao nhiêu mát dây đèn led để trang trí (làm tròn đến hàng đơn vị?
Đáp án: Lời giải và đáp án
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Nguyên hàm của hàm số \(y = {2^x}\) là
Đáp án : C Phương pháp giải :
Sử dụng công thức nguyên hàm của hàm số mũ \(\int {{a^x}dx} = \frac{{{a^x}}}{{\ln a}} + C\). Lời giải chi tiết :
\(\int {{2^x}dx} = \frac{{{2^x}}}{{\ln 2}} + C\).
Đáp án : A Phương pháp giải :
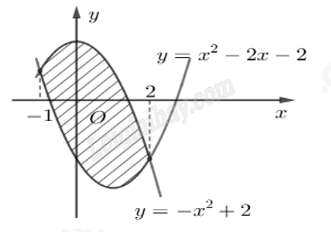
Diện tích hình phẳng giới hạn bởi y = f(x), y = g(x), x = a, x = b (a < b) là \(\int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \). Lời giải chi tiết :
Diện tích hình phẳng giới hạn bởi \(y = {x^2} - 2x - 2\), \(y = - {x^2} + 2\), x = -1, x = 2 là \(S = \int\limits_{ - 1}^2 {\left| {\left( {{x^2} - 2x - 2} \right) - \left( { - {x^2} + 2} \right)} \right|dx} = \int\limits_{ - 1}^2 {\left| {2{x^2} - 2x - 4} \right|dx} \). Vì trong khoảng (-1;2), \(2{x^2} - 2x - 4 < 0\) nên \(\left| {2{x^2} - 2x - 4} \right| = - \left( {2{x^2} - 2x - 4} \right) = - 2{x^2} + 2x + 4\). Vậy \(S = \int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \).
Câu 3 :
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
Đáp án : B Phương pháp giải :
Công thức tính số trung bình: \(\overline x = \frac{{{x_1}.{n_1} + ... + {x_m}.{n_m}}}{m}\), với \({x_1},...,{x_m}\) là giá trị đại diện của nhóm 1 đến m, \({n_1},...,{n_m}\) là tần số của nhóm 1 đến m. Lời giải chi tiết :
Bảng tần số ghép nhóm theo giá trị đại diện:
Số trung bình: \(\overline x = \frac{{2.6 + 7.8 + 7.10 + 3.12 + 1.14}}{{20}} = 9,4\). Vậy \(\overline x = 9,4 \in [9;11)\).
Câu 4 :
Trong không gian Oxyz, đường thẳng \(d:\left\{ \begin{array}{l}x = 2 - t\\y = 1 + 2t\\z = 3 + t\end{array} \right.\) có một vecto chỉ phương là
Đáp án : C Phương pháp giải :
Đường thẳng \(d:\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) có một vecto chỉ phương là \(\overrightarrow u = (a;b;c)\). Lời giải chi tiết :
Đường thẳng \(d:\left\{ \begin{array}{l}x = 2 - t\\y = 1 + 2t\\z = 3 + t\end{array} \right.\) có một vecto chỉ phương là \(\overrightarrow {{u_3}} = ( - 1;2;1)\).
Câu 5 :
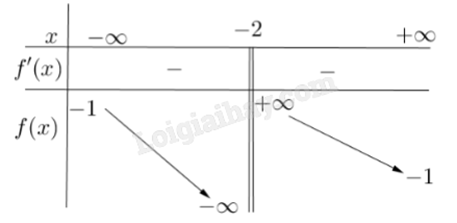
Cho hàm số y = f(x) có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình
Đáp án : D Phương pháp giải :
Hàm số y = f(x) có tiệm cận đứng x = a nếu thỏa mãn ít nhất một trong những điều kiện: \(\mathop {\lim }\limits_{x \to {a^ - }} f(x) = + \infty \), \(\mathop {\lim }\limits_{x \to {a^ - }} f(x) = - \infty \), \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = + \infty \), \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = - \infty \). Lời giải chi tiết :
Quan sát đồ thị, ta thấy \(\mathop {\lim }\limits_{x \to - {2^ - }} f(x) = - \infty \) và \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = + \infty \) nên y = f(x) có tiệm cận đứng là x = -2.
Câu 6 :
Tập nghiệm của bất phương trình \(\log x \ge 1\) là
Đáp án : C Phương pháp giải :
\(\log a \ge b \Leftrightarrow \left\{ \begin{array}{l}a > 0\\a \ge {10^b}\end{array} \right.\). Lời giải chi tiết :
\(\log x \ge 1 \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x \ge {10^1}\end{array} \right. \Leftrightarrow x \ge 10\).
Câu 7 :
Trong không gian Oxyz, cho mặt cầu (S): \({(x - 2)^2} + {(y + 1)^2} + {(z - 3)^2} = 4\). Tâm của (S) có tọa độ là
Đáp án : D Phương pháp giải :
Mặt cầu (S): \({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\) có tâm I(a;b;c). Lời giải chi tiết :
Mặt cầu (S): \({(x - 2)^2} + {(y + 1)^2} + {(z - 3)^2} = 4\) có tâm I(2;-1;3).
Câu 8 :
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA = SB = SC = SD. Khẳng định nào sau đây đúng?
Đáp án : B Phương pháp giải :
Sử dụng tính chất trung điểm. Lời giải chi tiết :
Xét tam giác SAC cân tại S có O là trung điểm của AC, suy ra SO vừa là trung truyến, vừa là đường cao của tam giác SAC. Do đó, \(SO \bot AC\). Chứng minh tương tự, ta được \(SO \bot BD\). Mà AC, BD cùng thuộc mặt phẳng (ABCD) và cắt nhau tại O. Vậy \(SO \bot (ABCD)\).
Câu 9 :
Tập nghiệm của bất phương trình \({2^x} \le 4\) là
Đáp án : A Phương pháp giải :
\(\left\{ \begin{array}{l}{a^x} \le b\\a > 1\end{array} \right. \Leftrightarrow x \le {\log _a}b\). Lời giải chi tiết :
\({2^x} \le 4 \Leftrightarrow x \le {\log _2}4 \Leftrightarrow x \le 2\).
Câu 10 :
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3\) và công bội q = 2. Giá trị của \({u_2}\) bằng
Đáp án : C Phương pháp giải :
Áp dụng công thức số hạng tổng quát của cấp số nhân: \({u_n} = {u_1}{q^{n - 1}}\). Lời giải chi tiết :
\({u_2} = {u_1}q = 3.2 = 6\).
Câu 11 :
Cho hình lập phương ABCD. A’B’C’D’. Mệnh đề nào sau đây sai?
Đáp án : D Phương pháp giải :
Xét từng đáp án, sử dụng phương pháp loại trừ. Áp dụng các quy tắc vecto: quy tắc hình bình hành, quy tắc hình hộp, khái niệm vecto bằng nhau, độ dài vecto. Lời giải chi tiết :
Đáp án A đúng theo quy tắc hình hộp. Đáp án B đúng theo quy tắc hình bình hành. Đáp án C đúng vì \(\left| {\overrightarrow {AB} } \right| = AB = CD = \left| {\overrightarrow {CD} } \right|\). Đáp án D sai vì \(\overrightarrow {AB} \), \(\overrightarrow {CD} \) là hai vecto ngược hướng nên chúng không bằng nhau.
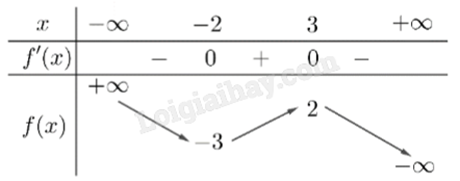
Đáp án : B Phương pháp giải :
Quan sát đồ thị và nhận xét. Lời giải chi tiết :
Dựa vào bảng biến thiên, ta thấy giá trị cực đại của hàm số đã cho là \({y_{CD}} = 2\).
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Cho phương trình lượng giác \(\sin 2x = - \frac{1}{2}\) (*). a) Phương trình (*) tương đương \(\sin 2x = \sin \left( { - \frac{\pi }{6}} \right)\).
Đúng
Sai
b) Trong khoảng \((0;\pi )\) phương trình (*) có 3 nghiệm.
Đúng
Sai
c) Tổng các nghiệm của phương trình (*) trong khoảng \((0;\pi )\) bằng \(\frac{{3\pi }}{2}\).
Đúng
Sai
d) Trong khoảng \((0;\pi )\) phương trình (*) có nghiệm lớn nhất bằng \(\frac{{7\pi }}{{12}}\).
Đúng
Sai
Đáp án
a) Phương trình (*) tương đương \(\sin 2x = \sin \left( { - \frac{\pi }{6}} \right)\).
Đúng
Sai
b) Trong khoảng \((0;\pi )\) phương trình (*) có 3 nghiệm.
Đúng
Sai
c) Tổng các nghiệm của phương trình (*) trong khoảng \((0;\pi )\) bằng \(\frac{{3\pi }}{2}\).
Đúng
Sai
d) Trong khoảng \((0;\pi )\) phương trình (*) có nghiệm lớn nhất bằng \(\frac{{7\pi }}{{12}}\).
Đúng
Sai
Phương pháp giải :
Nếu \(\sin \alpha = m\) thì \(\sin x = m \Leftrightarrow \sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\). Lời giải chi tiết :
a) Đúng. Vì \(\sin \left( { - \frac{\pi }{6}} \right) = - \frac{1}{2}\) nên \(\sin 2x = - \frac{1}{2} \Leftrightarrow \sin 2x = \sin \left( { - \frac{\pi }{6}} \right)\). b) Sai. (*) \(\begin{array}{l} \Leftrightarrow \sin 2x = \sin \left( { - \frac{\pi }{6}} \right) \Leftrightarrow \left[ \begin{array}{l}2x = - \frac{\pi }{6} + k2\pi \\2x = \pi - \left( { - \frac{\pi }{6}} \right) + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{{12}} + k\pi \\x = \frac{{7\pi }}{{12}} + k\pi \end{array} \right.\\\end{array}\) \((k \in \mathbb{Z})\). Vì \(0 < x < \pi \Rightarrow \left[ \begin{array}{l}0 < - \frac{\pi }{{12}} + k\pi < \pi \\0 < \frac{{7\pi }}{{12}} + k\pi < \pi \end{array} \right.(k \in \mathbb{Z}) \Leftrightarrow \left[ \begin{array}{l}k = 1\\k = 0\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = \frac{{11\pi }}{{12}}\\x = \frac{{7\pi }}{{12}}\end{array} \right.\). Vậy trong khoảng \((0;\pi )\) phương trình (*) có 2 nghiệm. c) Đúng. Tổng các nghiệm của phương trình (*) trong khoảng \((0;\pi )\) là: \(S = \frac{{11\pi }}{{12}} + \frac{{7\pi }}{{12}} = \frac{{3\pi }}{2}\). d) Sai. Vì \(\frac{{11\pi }}{{12}} > \frac{{7\pi }}{2}\) nên nghiệm lớn nhất của (*) trong khoảng \((0;\pi )\) là \(\frac{{11\pi }}{{12}}\).
Câu 2 :
Một ô tô bắt đầu chuyển động nhanh dần đều với tốc độ v(t) = 5t (m/s), trong đó t là thời gian tính bằng giây kể từ khi ô tô bắt đầu chuyển động. Đi được 6 (s) người lái xe phát hiện chương ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc a = −5 \((m/{s^2})\). a) Tốc độ của ô tô tại thời điểm 10 giây tính từ lúc xuất phát là 10 (m/s).
Đúng
Sai
b) Quãng đường ô tô chuyển động được trong 6 giây đầu tiên là 80 m.
Đúng
Sai
c) Quãng đường S (đơn vị: mét) mà ô tô chuyển động được kể từ lúc bắt đầu đạp phanh đến khi dừng lại được tính theo công thức \(S = \int\limits_0^6 {(30 - 5t)dt} \).
Đúng
Sai
d) Quãng đường ô tô chuyển động được kể từ lúc bắt đầu chuyển động cho đến khi dừng lại là 170 m.
Đúng
Sai
Đáp án
a) Tốc độ của ô tô tại thời điểm 10 giây tính từ lúc xuất phát là 10 (m/s).
Đúng
Sai
b) Quãng đường ô tô chuyển động được trong 6 giây đầu tiên là 80 m.
Đúng
Sai
c) Quãng đường S (đơn vị: mét) mà ô tô chuyển động được kể từ lúc bắt đầu đạp phanh đến khi dừng lại được tính theo công thức \(S = \int\limits_0^6 {(30 - 5t)dt} \).
Đúng
Sai
d) Quãng đường ô tô chuyển động được kể từ lúc bắt đầu chuyển động cho đến khi dừng lại là 170 m.
Đúng
Sai
Phương pháp giải :
Sử dụng công thức tính vận tốc \(v(t) = {v_0} + at\) với \({v_0}\) là vận tốc ban đầu, a là gia tốc, t là thời gian di chuyển. Tính quãng đường bằng cách tính tích phân của vận tốc. Lời giải chi tiết :
a) Đúng. Sau 6 giây đầu, vận tốc của ô tô đạt v(6) = 5.6 = 30 (m/s). Trong 4 giây tiếp theo, ô tô giảm vận tốc theo gia tốc a = -5 \((m/{s^2})\) nên vận tốc của ô tô sau 4 giây giảm tốc là v = 30 + (-5).4 = 10 (m/s). Vậy, sau 10 giây đầu thì vận tốc của ô tô là 10 (m/s). b) Sai. Quãng đường ô tô di chuyển được trong 6 giây đầu tiên là \({S_1} = \int\limits_0^6 {5tdt} = 90\) (m). c) Đúng. Gọi \({t_0}\) là thời gian tính bằng giây kể từ lúc ô tô phanh gấp cho đến khi dừng lại. Vận tốc của ô tô được tính bằng công thức v = 30 + (-5).t (m/s) với t được tính từ lúc bắt đầu phanh. Sau \({t_0}\) giây thì ô tô dừng hẳn nên ta có \(v = 30 + ( - 5).{t_0} = 0 \Leftrightarrow {t_0} = 6\) (giây). Như vậy, ô tô mất 6 giây để dừng hẳn kể từ lúc phanh. Trong quá trình đó, vận tốc của ô tô là v = 30 + (-5).t (m/s). Vậy, quãng đường ô tô đi được từ lúc phanh cho đến khi dừng hẳn là \({S_2} = \int\limits_0^6 {(30 - 5t)dt} = 90\) (m). d) Sai. Quãng đường ô tô đi được từ lúc bắt đầu chuyển động đến khi dừng hẳn là \(S = {S_1} + {S_2} = 90 + 90 = 180\) (m/s).
Câu 3 :
Lớp 12A có 30 học sinh, trong đó có 17 bạn nữ còn lại là nam. Có 3 bạn tên Hiền, trong đó có 1 bạn nữ và 2 bạn nam. Thầy giáo gọi ngẫu nhiên một bạn lên bảng. a) Xác suất học sinh được gọi tên Hiền là \(\frac{1}{{10}}\).
Đúng
Sai
b) Xác suất học sinh được gọi tên Hiền, biết học sinh đó là nữ là \(\frac{3}{{17}}\).
Đúng
Sai
c) Xác suất học sinh được gọi tên Hiền, biết học sinh đó là nam là \(\frac{2}{{13}}\).
Đúng
Sai
d) Nếu thầy giáo gọi một bạn tên Hiền lên bảng thì xác suất bạn đó là nam là \(\frac{3}{{17}}\).
Đúng
Sai
Đáp án
a) Xác suất học sinh được gọi tên Hiền là \(\frac{1}{{10}}\).
Đúng
Sai
b) Xác suất học sinh được gọi tên Hiền, biết học sinh đó là nữ là \(\frac{3}{{17}}\).
Đúng
Sai
c) Xác suất học sinh được gọi tên Hiền, biết học sinh đó là nam là \(\frac{2}{{13}}\).
Đúng
Sai
d) Nếu thầy giáo gọi một bạn tên Hiền lên bảng thì xác suất bạn đó là nam là \(\frac{3}{{17}}\).
Đúng
Sai
Phương pháp giải :
Áp dụng công thức xác suất của biến cố A với điều kiện B: \(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{P(A \cap B)}}{{P(B)}}\). Lời giải chi tiết :
A: “Học sinh được gọi tên Hiền”. B: “Học sinh được gọi là nữ”. C: “Học sinh được gọi là nam”. a) Đúng. Có 3 học sinh tên Hiền trong tổng số 30 học sinh nên \(P(A) = \frac{3}{{30}} = \frac{1}{{10}}\). b) Sai. Có 17 học sinh nữ trong lớp nên \(P(B) = \frac{{17}}{{30}}\). Có 1 học sinh nữ, tên Hiền nên \(P(AB) = \frac{1}{{30}}\). Xác suất để thầy giáo gọi Hiền lên bảng với điều kiện bạn đó là nữ là: \(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{\frac{1}{{30}}}}{{\frac{{17}}{{30}}}} = \frac{1}{{17}}\). c) Đúng. Có 30 – 17 = 13 học sinh nam trong lớp nên \(P(C) = \frac{{13}}{{30}}\). Có 2 học sinh nam, tên Hiền nên \(P(AC) = \frac{2}{{30}} = \frac{1}{{15}}\). Xác suất để thầy giáo gọi Hiền lên bảng với điều kiện bạn đó là nam là: \(P(A|C) = \frac{{P(AC)}}{{P(C)}} = \frac{{\frac{1}{{15}}}}{{\frac{{13}}{{30}}}} = \frac{2}{{13}}\). d) Sai. Xác suất để học sinh được gọi là nam, biết bạn đó tên Hiền là: \(P(C|A) = \frac{{P(AC)}}{{P(A)}} = \frac{{\frac{1}{{15}}}}{{\frac{1}{{10}}}} = \frac{2}{3}\).
Câu 4 :
Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm A(10;3;0) và chuyển động đều theo đường cáp có vectơ chỉ phương \(\overrightarrow u = (2; - 2;1)\), hướng chuyển động cùng chiều với hướng vectơ \(\overrightarrow u \) với tốc độ là 4,5 (m/s) (đơn vị trên mỗi trục là mét). a) Phương trình tham số của đường cáp là \(\left\{ \begin{array}{l}x = 10 + 2t\\y = 3 - 2t\\z = t\end{array} \right.\) \((t \in \mathbb{R})\).
Đúng
Sai
b) Giả sử sau thời gian t (giây) kể từ khi xuất phát \((t \ge 0)\), cabin đến điểm M. Khi đó, tọa độ điểm M là \(\left( {3t + 10; - 3t + 3;\frac{{3t}}{2}} \right)\).
Đúng
Sai
c) Cabin dừng ở điểm B có hoành độ \({x_B} = 550\), khi đó quãng đường AB dài 800 m.
Đúng
Sai
d) Đường cáp AB tạo với mặt phẳng (Oxy) một góc \({30^o}\).
Đúng
Sai
Đáp án
a) Phương trình tham số của đường cáp là \(\left\{ \begin{array}{l}x = 10 + 2t\\y = 3 - 2t\\z = t\end{array} \right.\) \((t \in \mathbb{R})\).
Đúng
Sai
b) Giả sử sau thời gian t (giây) kể từ khi xuất phát \((t \ge 0)\), cabin đến điểm M. Khi đó, tọa độ điểm M là \(\left( {3t + 10; - 3t + 3;\frac{{3t}}{2}} \right)\).
Đúng
Sai
c) Cabin dừng ở điểm B có hoành độ \({x_B} = 550\), khi đó quãng đường AB dài 800 m.
Đúng
Sai
d) Đường cáp AB tạo với mặt phẳng (Oxy) một góc \({30^o}\).
Đúng
Sai
Phương pháp giải :
Đường thẳng đi qua điểm \(M({x_0};{y_0};{z_0})\), nhận vecto \(\overrightarrow u = (a;b;c)\) làm vecto chỉ phương có phương trình tham số là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) \((t \in \mathbb{R})\). Lời giải chi tiết :
a) Đúng. Phương trình tham số của đường cáp là phương trình đường thẳng d đi qua điểm A(10;3;0) và nhận vecto \(\overrightarrow u = (2; - 2;1)\) làm vecto chỉ phương: \(\left\{ \begin{array}{l}x = 10 + 2t\\y = 3 - 2t\\z = t\end{array} \right.\) \((t \in \mathbb{R})\). b) Đúng. M thuộc d nên tọa độ của M là \(\left\{ \begin{array}{l}{x_M} = 10 + 2{t_M}\\{y_M} = 3 - 2{t_M}\\{z_M} = {t_M}\end{array} \right.\). Từ đó ta có \(\overrightarrow {AM} = \left( {10 + 2{t_M} - 10;3 - 2{t_M} - 3;{t_M} - 0} \right) = \left( {2{t_M}; - 2{t_M};{t_M}} \right)\). Suy ra \(AM = \sqrt {{{(2{t_M})}^2} + {{( - 2{t_M})}^2} + {{({t_M})}^2}} = 3{t_M}\). Theo giả thiết, cabin đi từ A với vận tốc 4,5 m/s trong t giây thì đến M nên AM = 4,5t (m). Do đó, \(3{t_M} = 4,5t \Leftrightarrow {t_M} = 1,5t\). Thay vào tọa độ điểm M, ta được \(\left\{ \begin{array}{l}{x_M} = 10 + 2.1,5t\\{y_M} = 3 - 2.1,5t\\{z_M} = 1,5t\end{array} \right. \Leftrightarrow M\left( {10 + 3t;3 - 3t;\frac{3}{2}t} \right)\). c) Sai. Từ câu b), ta tìm được tọa độ \(\left( {10 + 3t;3 - 3t;\frac{3}{2}t} \right)\) là vị trí của cabin sau t giây. Áp dụng với điểm B, giả sử sau \({t_B}\) giây thì cabin đến vị trí B, khi đó \(B\left( {10 + 3{t_B};3 - 3{t_B};\frac{3}{2}{t_B}} \right)\). Theo giả thiết, \({x_B} = 550\) nên \(10 + 3{t_B} = 550 \Leftrightarrow {t_B} = 180\). Quãng đường AB là \(AB = v.{t_B} = 4,5.180 = 810\) (m). d) Sai. Vecto chỉ phương của đường cáp là \(\overrightarrow u = (2; - 2;1)\), vecto pháp tuyến của mặt phẳng (Oxy) là \(\overrightarrow n = (0;0;1)\) nên ta có \(\sin \alpha = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}} = \frac{{2.0 - 2.0 + 1.1}}{{\sqrt {{2^2} + {{( - 2)}^2} + {1^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{1}{3}\) với \(\alpha \) là góc giữa đường cáp và mặt phẳng (Oxy). Suy ra \(\alpha \approx {19^o}\).
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
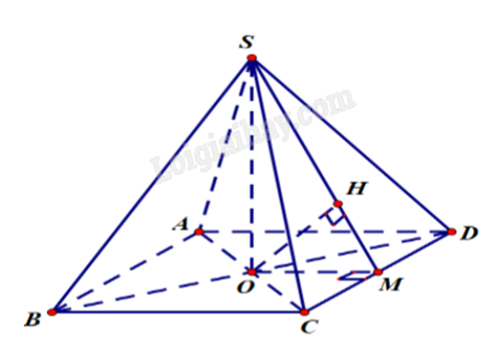
Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng 2, cạnh bên bằng \(2\sqrt 2 \). Tính khoảng cách giữa hai đường thẳng AB và SD (kết quả làm tròn đến hàng phần mười). Đáp án: Đáp án
Đáp án: Phương pháp giải :
Đưa về tìm khoảng cách từ một điểm đến mặt phẳng, áp dụng quan hệ song song. Lời giải chi tiết :
Gọi O là giao điểm của AC, BD. Khi đó, AC = 2OC. Vì AB // (SCD) suy ra \(d(AB;SD) = d(AB;(SCD)) = d(A;(SCD)) = 2d(O;(SCD))\). Trong mặt phẳng (ABCD), dựng \(OM \bot CD = M\). Trong mặt phẳng (SOM), dựng \(OH \bot SM = H\). Ta có \(\left\{ \begin{array}{l}OH \bot SM\\OH \bot CD\end{array} \right.\) suy ra \(OH \bot (SCD)\), do đó \(d(O;(SCD)) = OH\). \(OM = \frac{1}{2}AD = \frac{1}{2}.2 = 1\); \(OC = \frac{1}{2}AC = \frac{1}{2}\sqrt {A{B^2} + B{C^2}} = \frac{1}{2}\sqrt {{2^2} + {2^2}} = \sqrt 2 \); \(SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {{{(2\sqrt 2 )}^2} - {{(\sqrt 2 )}^2}} = \sqrt 6 \). Xét tam giác SOM vuông tại O, OH là đường cao: \(\frac{1}{{O{H^2}}} = \frac{1}{{O{M^2}}} + \frac{1}{{S{O^2}}} = \frac{1}{{{1^2}}} + \frac{1}{{{{\left( {\sqrt 6 } \right)}^2}}} = \frac{7}{6}\). Suy ra \(OH = \frac{{\sqrt {42} }}{7} = d(O;(SCD))\). Vậy \(d(AB;SD) = 2d(O;(SCD)) = \frac{{2\sqrt {42} }}{7} \approx 1,9\).
Câu 2 :
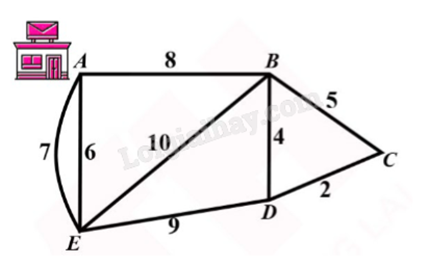
Một người đưa thư xuất phát từ vị trí A, các điểm cần phát thư nằm dọc con đường đi qua. Biết rằng người này phải đi trên mỗi con đường ít nhất một lần (để phát được thư cho tất cả các điểm cần phát nằm dọc theo con đường đó) và cuối cùng quay lại điểm xuất phát. Độ dài các con đường như hình vẽ (đơn vị độ dài). Hỏi tổng quãng đường người đưa thư có thể đi ngắn nhất có thể là bao nhiêu?
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng định lí về đường đi Euler. Lời giải chi tiết :
Theo sơ đồ đường đi thấy có 2 đỉnh bậc lẻ là A và D nên có thể tìm được một đường đi Euler từ A đến D (đường này đi qua mỗi cạnh đúng một lần).
Câu 3 :
Khi gắn hệ tọa độ Oxyz (đơn vị trên mỗi trục tính theo kilomet) vào một sân bay, mặt phẳng Oxy trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí A(5;0;5) đến vị trí B(10;10;3) và hạ cánh tại vị trí M(a;b;0). Giá trị của a + b bằng bao nhiêu (viết kết quả dưới dạng số thập phân)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tìm giao của đường thẳng AB với mặt phẳng (Oxy). Lời giải chi tiết :
Ta có \(\overrightarrow {AB} = (5;10; - 2)\) nên phương trình đường thẳng AB là \(\left\{ \begin{array}{l}x = 5 + 5t\\y = 10t\\z = 5 - 2t\end{array} \right.\). Vì M thuộc đường thẳng AB nên \(\left\{ \begin{array}{l}{x_M} = 5 + 5{t_M}\\{y_M} = 10{t_M}\\{z_M} = 5 - 2{t_M}\end{array} \right.\). Ngoài ra, M thuộc mặt phẳng (Oxy) nên \({z_M} = 0 \Leftrightarrow 5 - 2{t_M} = 0 \Leftrightarrow {t_M} = \frac{5}{2}\). Suy ra M(17,5;25;0). Vậy a + b = 17,5 + 25 = 42,5.
Câu 4 :
Một bể chứa nhiên liệu hình trị đặt nằm ngang, có chiều dài 5 m, bán kính đáy 1 m. Chiều cao của mực nhiên liệu là 1,5 m. Tính thể tích phần nhiên liệu trong bể (theo đơn vị \({m^3}\), làm tròn đến hàng phần chục).
Đáp án: Đáp án
Đáp án: Phương pháp giải :
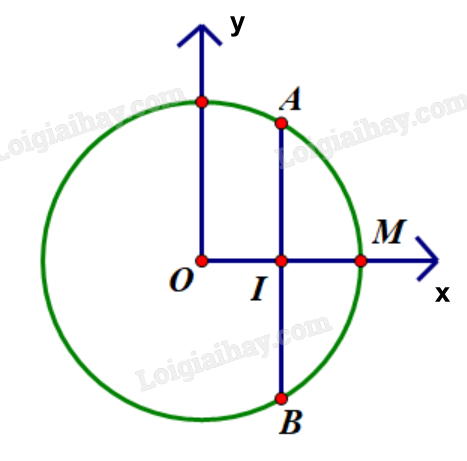
Áp dụng ứng dụng hình học của tích phân: + Tìm hàm số của đồ thị đường tròn và đường thẳng giới hạn mực nước đáy bể. + Tính diện tích đáy và thể tích của phần bể trống nhiên liệu. + Lấy thể tích bể chứa trừ đi thể tích phần bể trống để tìm thể tích nhiên liệu. Lời giải chi tiết :
Thể tích của cả bể nhiên liệu là: \(V = \pi {r^2}h = \pi {.1^2}.5 = 5\pi \) \(({m^3})\). Gọi \({V_1}\) là thể tích phần trống nhiên liệu, \({V_2}\) là phần thể tích chứa nhiên liệu. Khi đó \({V_2} = V - {V_1}\). Đề tìm \({V_2}\) theo yêu cầu đề bài, ta tính \({V_1}\) trước. \({V_1} = {B_{trong}}.h\), với \({B_{trong}}\) là phần diện tích đáy không chứa nhiên liệu. Chọn hệ trục Oxy như hình vẽ:
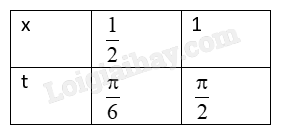
Đường tròn đáy là đường tròn tâm O, bán kính R = 1 nên có phương trình \({x^2} + {y^2} = 1\). Khi đó phần đồ thị nửa đường tròn nằm trên trục hoành có phương trình \(y = \sqrt {1 - {x^2}} \). Chiều cao nhiên liệu là 1,5 m, bán kính đáy bằng 1 m nên \(I\left( {\frac{1}{2};0} \right)\), \(M\left( {1;0} \right)\). Thiết diện phần trống là diện tích hình phẳng tạo bởi cung nhỏ AB và đoạn thẳng AB, tức là hai lần diện tích tạo bởi cung nhỏ AM của đường tròn, trục hoành (đoạn IM) và đường thẳng \(x = \frac{1}{2}\) (đoạn AI). \({B_{trong}} = 2\int\limits_{\frac{1}{2}}^1 {\sqrt {1 - {x^2}} dx} \). Để tính \(\int\limits_{\frac{1}{2}}^1 {\left( {\sqrt {1 - {x^2}} } \right)dx} \), ta đặt \(x = \sin t \Rightarrow dx = \cos tdt\). Đổi cận:
Khi đó \(\int\limits_{\frac{1}{2}}^1 {\left( {\sqrt {1 - {x^2}} } \right)dx} {\rm{\;}} = \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}} {\left( {\sqrt {1 - {{\sin }^2}t} } \right)\cos tdt} {\rm{\;}} = \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}} {\left| {\cos t} \right|\cos tdt} {\rm{\;}} = \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}} {{{\cos }^2}tdt} \) (vì trong khoảng \(\left( {\frac{\pi }{6};\frac{\pi }{2}} \right)\) ta có \(\cos t > 0 \Rightarrow \left| {\cos t} \right| = \cos t\)). Suy ra \(\int\limits_{\frac{1}{2}}^1 {\left( {\sqrt {1 - {x^2}} } \right)dx} {\rm{\;}} = \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}} {{{\cos }^2}tdt} {\rm{\;}} = \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}} {\frac{{1 + \cos 2x}}{2}tdt} {\rm{\;}} = \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}} {\left( {\frac{1}{2} + \frac{{\cos 2x}}{2}} \right)tdt} \) \( = \left( {\frac{x}{2} + \frac{{\sin 2x}}{4}} \right)\left| {\begin{array}{*{20}{c}}{^{\frac{\pi }{2}}}\\{_{\frac{\pi }{6}}}\end{array}} \right. = \frac{\pi }{4} + \frac{{\sin \pi }}{4} - \left( {\frac{\pi }{{12}} + \frac{{\sin \frac{\pi }{3}}}{4}} \right) = \frac{\pi }{6} - \frac{{\sqrt 3 }}{8}\). \({B_{trong}} = 2\int\limits_{\frac{1}{2}}^1 {\left( {\sqrt {1 - {x^2}} } \right)dx} {\rm{\;}} = 2\left( {\frac{\pi }{6} - \frac{{\sqrt 3 }}{8}} \right) = \frac{\pi }{3} - \frac{{\sqrt 3 }}{4}\). \({V_1} = {B_{trong}}.h = 5\left( {\frac{\pi }{3} - \frac{{\sqrt 3 }}{4}} \right)\). Thể tích phần nhiên liệu trong bể là \({V_2} = V - {V_1} = 5\pi {\rm{\;}} - 5\left( {\frac{\pi }{3} - \frac{{\sqrt 3 }}{4}} \right) \approx 12,6\) \(({m^3})\).
Câu 5 :
Nhà máy A chuyển sản xuất một loại sản phẩm cho nhà máy B. Hai nhà máy thỏa thuận rằng, hằng tháng A cung cấp cho B số lượng sản phẩm theo đơn đặt hàng của B (tối đa 100 tấn sản phẩm). Nếu số lượng đặt hàng là x tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là \(P(x) = 45 - 0,001{x^2}\) (triệu đồng). Chi phí để A sản xuất x tấn sản phẩm trong một tháng là \(C(x) = 100 + 30x\) triệu đồng (gồm 100 triệu đồng chi phí cố định và 30 triệu đồng cho mỗi tấn sản phẩm). Nhà máy A bán cho B bao nhiêu tấn sản phẩm để lợi nhuận thu được là lớn nhất (làm tròn kết quả đến hàng phần mười)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Lập hàm số tính lợi nhuận của nhà máy (Lợi nhuận = Doanh thu – Chi phí). Tìm giá trị lớn nhất của hàm số vừa tìm được trên đoạn [0;100]. Lời giải chi tiết :
Doanh thu của nhà máy khi sản xuất 1 tấn sản phẩm là P(x) triệu đồng. Doanh thu của nhà máy khi sản xuất x tấn sản phẩm là xP(x) triệu đồng. Chi phí của nhà máy khi sản xuất x tấn sản phẩm là C(x) triệu đồng. Vì Lợi nhuận = Doanh thu – Chi phí nên ta có lợi nhuận của nhà máy A khi sản xuất x tấn sản phẩm là: \(H(x) = xP(x) - C(x) = x(45 - 0,001{x^2}) - (100 + 30x) = - 0,001{x^3} + 15x - 100\), với \(0 \le x \le 100\). \(H'(x) = - 0,003{x^2} + 15\). \(H'(x) = 0 \Leftrightarrow - 0,003{x^2} + 15 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 50\sqrt 2 \\x = - 50\sqrt 2 \end{array} \right.\) Chỉ có \(x = 50\sqrt 2 \) thỏa mãn điều kiện. Ta có: \(H(0) = - 100\); \(H(50\sqrt 2 ) = 500\sqrt 2 \); \(H(100) = 400\). Vậy lợi nhuận lớn nhất khi A sản xuất \(50\sqrt 2 \approx 70,7\) tấn sản phẩm.
Câu 6 :
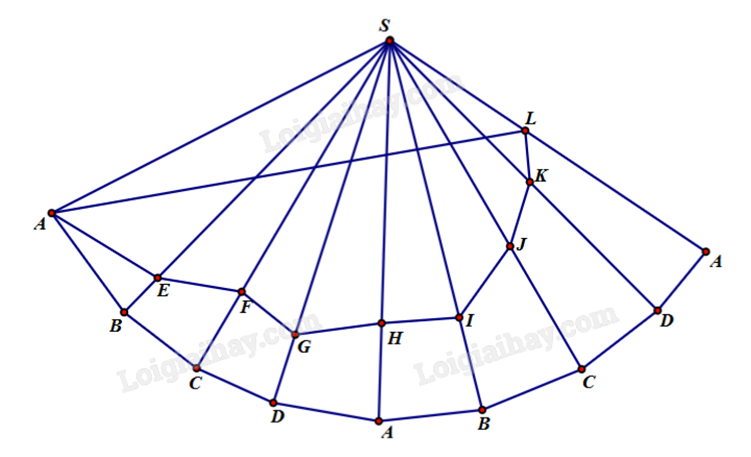
Người ta cần trang trí một kim tự tháp hình chóp tứ giác đều S.ABCD cạnh bên bằng 200 m, góc \(\widehat {ASB} = {15^o}\) bằng đường gấp khúc dây đèn led vòng quanh kim tự tháp AEFGHIJKLS. Trong đó, điểm L cố định và LS = 40 m. Hỏi, khi đó cần dùng ít nhất bao nhiêu mát dây đèn led để trang trí (làm tròn đến hàng đơn vị?
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng phương pháp trải đa diện và định lí cosin trong tam giác. Lời giải chi tiết :
Cắt hình chóp theo cạnh bên SA rồi trải ra mặt phẳng hai lần, ta có hình vẽ sau:
Từ đó suy ra chiều dài dây đèn led ngắn nhất bằng AL + LS. Vì S.ABCD là hình chóp đều nên \(\widehat {ASL} = {8.15^o} = {120^o}\). Sử dụng định lí cosin cho tam giác ASL, ta có: \(A{L^2} = S{A^2} + S{L^2} - 2.SA.SL.\cos \widehat {ASL} = {200^2} + {40^2} - 2.200.40.\cos {120^o} = 49600\). Suy ra \(AL = \sqrt {49600} = 40\sqrt {31} \). Vậy chiều dài dây đèn led cần ít nhất là \(40\sqrt {31} + 40 \approx 263\) mét. |