Đề tham khảo thi THPT môn Toán - Đề số 2 (hay, chi tiết)I. Phần trắc nghiệmĐề bài
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Nguyên hàm của hàm số f(x) = sinx là
Câu 2 :
Cho hàm số y = f(x) xác định và liên tục trên đoạn [a;b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b được tính theo công thức
Câu 3 :
Cô Hà thống kê lại đường kính thân gốc của một số cây xoan đào 6 năm tuổi được trồng ở một lâm trường ở bảng sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Câu 4 :
Trong không gian Oxyz, cho hai điểm M(1;2;1) và N(3;1;-2). Đường thẳng MN có phương trình là
Câu 5 :
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{4x + 1}}{{x - 1}}\) là
Câu 6 :
Với a là số thực dương tùy ý, \({\log _4}(4a)\) bằng
Câu 7 :
Trong không gian Oxyz, cho mặt phẳng (P): 2x + 4y – z = 3. Vecto nào sau đây là vecto pháp tuyến của (P)?
Câu 8 :
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh SA vuông góc với đáy. Khẳng định nào sau đây đúng?
Câu 9 :
Nghiệm của phương trình \({\log _2}(x - 1) = 3\) là
Câu 10 :
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và công bội q = 3. Tìm số hạng thứ 4 của cấp số nhân.
Câu 11 :
Cho hình hộp ABCD. A’B’C’D’. Phát biểu nào sau đây đúng?
Câu 12 :
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Cho hàm số f(x) = sin2x – x. a) \(f\left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2}\); \(f\left( {\frac{\pi }{2}} \right) = - \frac{\pi }{2}\).
Đúng
Sai
b) Đạo hàm của hàm số đã cho là f’(x) = cos2x – 1.
Đúng
Sai
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{6}\) hoặc \(\frac{\pi }{6}\).
Đúng
Sai
d) Giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{2}\).
Đúng
Sai
Câu 2 :
Sự phân hủy của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hòa tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ (\(t \ge 0\)) khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số \(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\). a) Vào thời điểm t = 1 thì nồng độ oxygen trong nước là 3,5 (mg/l).
Đúng
Sai
b) Nồng độ oxygen (mg/l) trong hồ nước không vượt quá 5 (mg/l).
Đúng
Sai
c) Vào thời điểm t = 0 thì nồng độ oxygen trong nước cao nhất.
Đúng
Sai
d) Nồng độ oxygen (mg/l) trong hồ nước thấp nhất là 3,5 (mg/l).
Đúng
Sai
Câu 3 :
Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là 0,4 và khả năng thắng thầu của dự án 2 là 0,5. Khả năng thắng thầu cả 2 dự án là 0,3. Gọi A là biến cố: “Thắng thầy dự án 1”, B là biến cố: “Thắng thầu dự án 2”. a) A và B là hai biến cố độc lập.
Đúng
Sai
b) Xác suất để công ty thắng thầu đúng 1 dự án bằng 0,7.
Đúng
Sai
c) Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là 0,75.
Đúng
Sai
d) Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là 0,25.
Đúng
Sai
Câu 4 :
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục toạ độ là kilomet), một máy bay đang ở vị trí A(3,5;2;0,4) và sẽ hạ cánh ở vị trí B(3,5;5,5;0) trên đường băng EG (hình vẽ). a) Đường thẳng AB có phương trình tham số là \(\left\{ \begin{array}{l}x = 3,5\\y = - 2 + 7,5t\\z = 0,4 - 0,4t\end{array} \right.\) \((t \in \mathbb{R})\).
Đúng
Sai
b) Khi máy bay ở vị trí D(3,5;3,25;0,12) thì máy bay cách mặt đất 120 m.
Đúng
Sai
c) Có một lớp mây được mô phỏng bởi một mặt phẳng \((\alpha )\) đi qua ba điểm M(5;0;0), N(0;-5;0), P(0;0;0,5). Vị trí mà máy bay xuyên qua đám mây để hạ cánh là \(C\left( {\frac{7}{2};\frac{{47}}{{44}};\frac{{13}}{{55}}} \right)\).
Đúng
Sai
d) Theo quy định an toàn bay, người phi công phải nhìn thấy điểm đầu E(3,5;4,5;0) của đường băng ở độ cao tối thiểu là 120 m. Nếu sau khi ra khỏi đám mây, tầm nhìn của người phi công là 900 m thì người phi công đã không đạt được quy định an toàn bay. (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
Đúng
Sai
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Cho tứ diện đều ABCD có cạnh bằng 2. Khoảng cách giữa hai đường thẳng AB và CD bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)? Đáp án:
Câu 2 :
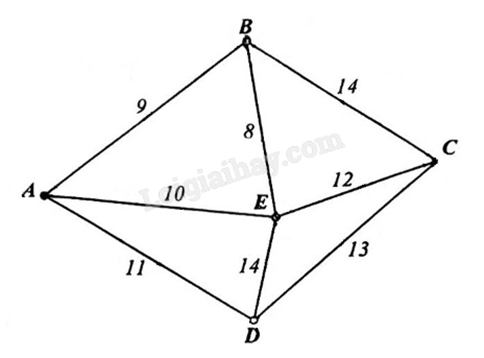
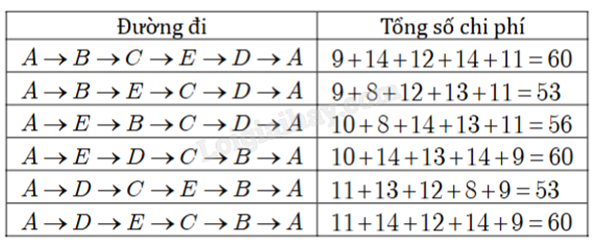
Một công ty vận tải cần giao hàng đến tất cả các thành phố A, B, C, D, E (hình vẽ bên dưới). Chi phí di chuyển giữa các thành phố được mô tả trên hình. Xe giao hàng của công ty xuất phát từ một thành phố trong năm thành phố trên đi qua tất cả các thành phố còn lại đúng một lần sau đó trở lại thành phố ban đầu. Tìm chi phí thấp nhất của xe giao hàng.
Đáp án:
Câu 3 :
Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ tọa độ Oxyz như hình vẽ với độ dài đơn vị trên các trục tọa độ bằng 1 m. Biết . Tính x + 2y – z (làm tròn kết quả đến hàng phần mười).
Đáp án:
Câu 4 :
Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là AB = 8 m. Người treo một tấm phông hình chữ nhật có hai đỉnh M, N nằm trên Parabol và hai đỉnh P, Q nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta mua hoa để trang trí hoa, biết MN = 4 m, MQ = 6 m. Diện tích phần phía ngoài phông để trang trí hoa (phần không tô đen) là bao nhiêu mét vuông (kết quả làm tròn đến hàng phần mười)? Đáp án:
Câu 5 :
Có hai xã A, B cùng ở một bên bờ sông. Khoảng cách từ hai xã đó đến bờ sông lần lượt là AA′ = 500 m, BB′ = 600 m. Người ta đo được A’B’ = 2200 m như hình vẽ dưới đây. Các kỹ sư muốn xây dựng một trạm cung cấp nước sạch nằm bên bờ sông cho người dân của hai xã sử dụng. Để tiết kiệm chi phí, các kỹ sư phải chọn một vị trí M của trạm cung cấp nước sạch đó trên đoạn A’B’ sao cho tổng khoảng cách từ hai xã đến vị trí M là nhỏ nhất. Giá trị nhỏ nhất của tổng khoảng cách đó bằng bao nhiêu mét (làm tròn đến hàng đơn vị)? Đáp án:
Câu 6 :
Một căn bệnh có 1% dân số mắc phải. Một phương pháp chuẩn đoán được phát triển có tỷ lệ chính xác là 99%. Với những người bị bệnh, phương pháp này sẽ đưa ra kết quả dương tính 99% số trường hợp. Với người không mắc bệnh, phương pháp này cũng chuẩn đoán đúng 99 trong 100 trường hợp. Nếu một người kiểm tra và kết quả là dương tính (bị bệnh), xác suất để người đó thực sự bị bệnh là bao nhiêu (kết quả viết dưới dạng số thập phân)? Đáp án: Lời giải và đáp án
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Nguyên hàm của hàm số f(x) = sinx là
Đáp án : C Phương pháp giải :
Sử dụng công thức nguyên hàm của hàm số lượng giác. Lời giải chi tiết :
\(\int {\sin xdx} = - \cos x + C\).
Câu 2 :
Cho hàm số y = f(x) xác định và liên tục trên đoạn [a;b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b được tính theo công thức
Đáp án : A Phương pháp giải :
Sử dụng công thức tính diện tích hình phẳng thông qua tích phân. Lời giải chi tiết :
Diện tích hình phẳng giới hạn bởi y = f(x), trục hoành, x = a, x = b (a < b) là \(\int\limits_a^b {\left| {f(x)} \right|dx} \).
Câu 3 :
Cô Hà thống kê lại đường kính thân gốc của một số cây xoan đào 6 năm tuổi được trồng ở một lâm trường ở bảng sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Đáp án : A Phương pháp giải :
Để tính khoảng biến thiên của mẫu số liệu ghép nhóm, ta lấy đầu mút phải của nhóm cuối cùng trừ đi đầu mút trái của nhóm đầu tiên. Lời giải chi tiết :
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là R = 65 – 40 = 25 (cm).
Câu 4 :
Trong không gian Oxyz, cho hai điểm M(1;2;1) và N(3;1;-2). Đường thẳng MN có phương trình là
Đáp án : B Phương pháp giải :
Đường thẳng có vecto chỉ phương \(\overrightarrow u = (a;b;c)\), đi qua điểm \(M({x_0};{y_0};{z_0})\) có phương trình là \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\). Lời giải chi tiết :
\(\overrightarrow {MN} = (2; - 1; - 3)\) là vecto chỉ phương của đường thẳng MN, lại có M(1;2;1) thuộc MN nên phương trình đường thẳng là \(\frac{{x - 1}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 1}}{{ - 3}}\).
Câu 5 :
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{4x + 1}}{{x - 1}}\) là
Đáp án : B Phương pháp giải :
Hàm số y = f(x) có tiệm cận ngang y = a nếu thỏa mãn ít nhất một trong những điều kiện: \(\mathop {\lim }\limits_{x \to + \infty } f(x) = a\), \(\mathop {\lim }\limits_{x \to - \infty } f(x) = a\). Lời giải chi tiết :
Ta có \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{4x + 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {4 + \frac{1}{x}} \right)}}{{x\left( {1 - \frac{1}{x}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{4 + \frac{1}{x}}}{{1 - \frac{1}{x}}} = \frac{{4 + 0}}{{1 - 0}} = 4\). Vậy tiệm cận ngang của đồ thị hàm số \(y = \frac{{4x + 1}}{{x - 1}}\) là y = 4.
Câu 6 :
Với a là số thực dương tùy ý, \({\log _4}(4a)\) bằng
Đáp án : B Phương pháp giải :
Áp dụng các tính chất của phép tính logarit: \({\log _a}a = 1\); \({\log _a}bc = {\log _a}b + {\log _b}c\). Lời giải chi tiết :
\({\log _4}(4a) = lo{g_4}4 + {\log _4}a = 1 + {\log _4}a\).
Câu 7 :
Trong không gian Oxyz, cho mặt phẳng (P): 2x + 4y – z = 3. Vecto nào sau đây là vecto pháp tuyến của (P)?
Đáp án : A Phương pháp giải :
Vecto pháp tuyến của đường thẳng ax + by + cz + d = 0 là \(\overrightarrow n = (a;b;c)\). Lời giải chi tiết :
Vecto pháp tuyến của đường thẳng 2x + 4y – z = 3 là \(\overrightarrow {{n_1}} = (2;4; - 1)\).
Câu 8 :
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh SA vuông góc với đáy. Khẳng định nào sau đây đúng?
Đáp án : C Phương pháp giải :
Một đường thẳng vuông góc với một măt phẳng nếu đường thẳng đó vuông góc với hai đường thẳng cắt nhau thuộc mặt phẳng. Lời giải chi tiết :
Vì \(SA \bot (ABC)\) nên \(SA \bot BC\). Ta có \(\left\{ \begin{array}{l}SA \bot BC\\AB \bot BC\\SA \cap AB = A\end{array} \right.\) suy ra \(BC \bot (SAB)\).
Câu 9 :
Nghiệm của phương trình \({\log _2}(x - 1) = 3\) là
Đáp án : C Phương pháp giải :
\({\log _a}b = x \Leftrightarrow \left\{ \begin{array}{l}b > 0\\b = {a^x}\end{array} \right.\). Lời giải chi tiết :
\({\log _2}(x - 1) = 3 \Leftrightarrow \left\{ \begin{array}{l}x - 1 > 0\\x - 1 = {2^3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 1\\x = 9\end{array} \right. \Leftrightarrow x = 9\).
Câu 10 :
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và công bội q = 3. Tìm số hạng thứ 4 của cấp số nhân.
Đáp án : B Phương pháp giải :
Áp dụng công thức số hạng tổng quát của cấp số nhân: \({u_n} = {u_1}{q^{n - 1}}\). Lời giải chi tiết :
\({u_4} = {u_1}{q^3} = {2.3^3} = 54\).
Câu 11 :
Cho hình hộp ABCD. A’B’C’D’. Phát biểu nào sau đây đúng?
Đáp án : B Phương pháp giải :
Áp dụng quy tắc hình hộp, xét từng đáp án. Lời giải chi tiết :
Theo quy tắc hình hộp, chỉ có \(\overrightarrow {DB'} = \overrightarrow {DA} + \overrightarrow {DD'} + \overrightarrow {DC} \) đúng.
Câu 12 :
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Đáp án : A Phương pháp giải :
Hàm số f(x) nghịch biến khi f’(x) < 0. Lời giải chi tiết :
Dựa vào bảng xét dấu, thấy f’(x) < 0 trên khoảng \(( - 3;0)\) và \((2; + \infty )\). Trong các đáp án, chỉ có khoảng \(( - 3;0)\) thỏa mãn.
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Cho hàm số f(x) = sin2x – x. a) \(f\left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2}\); \(f\left( {\frac{\pi }{2}} \right) = - \frac{\pi }{2}\).
Đúng
Sai
b) Đạo hàm của hàm số đã cho là f’(x) = cos2x – 1.
Đúng
Sai
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{6}\) hoặc \(\frac{\pi }{6}\).
Đúng
Sai
d) Giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{2}\).
Đúng
Sai
Đáp án
a) \(f\left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2}\); \(f\left( {\frac{\pi }{2}} \right) = - \frac{\pi }{2}\).
Đúng
Sai
b) Đạo hàm của hàm số đã cho là f’(x) = cos2x – 1.
Đúng
Sai
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{6}\) hoặc \(\frac{\pi }{6}\).
Đúng
Sai
d) Giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{2}\).
Đúng
Sai
Phương pháp giải :
a) Thay \( - \frac{\pi }{2}\), \(\frac{\pi }{2}\) vào x của phương trình rồi tính. b) Áp dụng công thức đạo hàm của hàm hợp lượng giác: (sinu)’ = u’.cosu. c) Nếu \(\cos \alpha = m\) thì \(\cos x = m \Leftrightarrow \cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\). Dựa vào khoảng hoặc đoạn đề bài cho, tìm các giá trị k thỏa mãn rồi thay vào công thức nghiệm và kết luận. d) Thay giá trị hai đầu mút của đoạn và các giá trị sao cho f’(x) = 0 vào f(x) và tìm giá trị nhỏ nhất. Lời giải chi tiết :
a) Đúng. \(f\left( { - \frac{\pi }{2}} \right) = \sin ( - \pi ) - \left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2}\) và \(f\left( {\frac{\pi }{2}} \right) = \sin (\pi ) - \frac{\pi }{2} = - \frac{\pi }{2}\). b) Sai. f’(x) = 2cos2x – 1. c) Đúng. \(2\cos 2x - 1 = 0 \Leftrightarrow \cos 2x = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{3} + k2\pi \\2x = - \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x = - \frac{\pi }{6} + k\pi \end{array} \right.\) \((k \in \mathbb{Z})\). +) \( - \frac{\pi }{2} \le x \le \frac{\pi }{2} \Leftrightarrow - \frac{\pi }{2} \le \frac{\pi }{6} + k\pi \le \frac{\pi }{2} \Leftrightarrow - \frac{{2\pi }}{3} \le k\pi \le \frac{\pi }{3} \Leftrightarrow - \frac{2}{3} \le k \le \frac{1}{3} \Rightarrow k = 0\) (vì \(k \in \mathbb{Z}\)). Suy ra \(x = \frac{\pi }{6} + 0.\pi = \frac{\pi }{6}\). +) \( - \frac{\pi }{2} \le x \le \frac{\pi }{2} \Rightarrow - \frac{\pi }{2} \le - \frac{\pi }{6} + k\pi \le \frac{\pi }{2} \Leftrightarrow - \frac{\pi }{3} \le k\pi \le \frac{{2\pi }}{3} \Leftrightarrow - \frac{1}{3} \le k \le \frac{2}{3} \Rightarrow k = 0\) (vì \(k \in \mathbb{Z}\)). Suy ra \(x = - \frac{\pi }{6} + 0.\pi = - \frac{\pi }{6}\). Vậy trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) thì f’(x) = 0 có hai nghiệm là \(x = \frac{\pi }{6}\); \(x = - \frac{\pi }{6}\). d) Đúng. f(x) = sin2x – x; f’(x) = 2cos2x – 1 có nghiệm \(x = \pm \frac{\pi }{6} \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\). \(f\left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2}\); \(f\left( {\frac{\pi }{2}} \right) = - \frac{\pi }{2}\); \(f\left( { - \frac{\pi }{6}} \right) = \sin \left( { - \frac{\pi }{3}} \right) - \left( { - \frac{\pi }{6}} \right) = - \frac{{\sqrt 3 }}{2} + \frac{\pi }{6}\); \(f\left( {\frac{\pi }{6}} \right) = \sin \frac{\pi }{3} - \frac{\pi }{6} = \frac{{\sqrt 3 }}{2} - \frac{\pi }{6}\). Vậy giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{2}\).
Câu 2 :
Sự phân hủy của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hòa tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ (\(t \ge 0\)) khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số \(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\). a) Vào thời điểm t = 1 thì nồng độ oxygen trong nước là 3,5 (mg/l).
Đúng
Sai
b) Nồng độ oxygen (mg/l) trong hồ nước không vượt quá 5 (mg/l).
Đúng
Sai
c) Vào thời điểm t = 0 thì nồng độ oxygen trong nước cao nhất.
Đúng
Sai
d) Nồng độ oxygen (mg/l) trong hồ nước thấp nhất là 3,5 (mg/l).
Đúng
Sai
Đáp án
a) Vào thời điểm t = 1 thì nồng độ oxygen trong nước là 3,5 (mg/l).
Đúng
Sai
b) Nồng độ oxygen (mg/l) trong hồ nước không vượt quá 5 (mg/l).
Đúng
Sai
c) Vào thời điểm t = 0 thì nồng độ oxygen trong nước cao nhất.
Đúng
Sai
d) Nồng độ oxygen (mg/l) trong hồ nước thấp nhất là 3,5 (mg/l).
Đúng
Sai
Phương pháp giải :
a) Thay t = 1 vào hàm số và tính giá trị của hàm số. b), c), d) Lập bảng biến thiên của hàm số và nhận xét. Lời giải chi tiết :
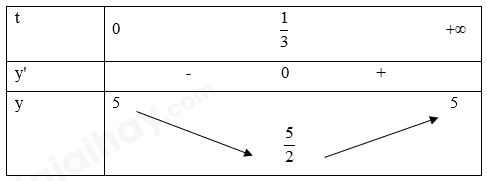
a) Đúng. \(y(1) = 5 - \frac{{15}}{{{{9.1}^2} + 1}} = 3,5\) (mg/l). b) Đúng. Xét \(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\) trên nửa đoạn \([0; + \infty )\): \(y'(t) = \frac{{135{t^2} - 15}}{{9{t^2} + 1}} = 0 \Leftrightarrow \left[ \begin{array}{l}t = \frac{1}{3}\\t = - \frac{1}{3}\end{array} \right.\). Ta có bảng biến thiên:
Từ bảng biến thiên, ta thấy giá trị của \(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\) luôn nhỏ hơn hoặc bằng 5 nên nồng độ oxygen (mg/l) trong hồ nước không vượt quá 5. c) Đúng. Quan sát bảng biến thiên, thấy vào thời điểm t = 0 thì nồng độ oxygen trong nước cao nhất bằng 5. d) Sai. Quan sát bảng biến thiên, thấy nồng độ oxygen (mg/l) trong hồ nước thấp nhất là 2,5 (mg/l).
Câu 3 :
Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là 0,4 và khả năng thắng thầu của dự án 2 là 0,5. Khả năng thắng thầu cả 2 dự án là 0,3. Gọi A là biến cố: “Thắng thầy dự án 1”, B là biến cố: “Thắng thầu dự án 2”. a) A và B là hai biến cố độc lập.
Đúng
Sai
b) Xác suất để công ty thắng thầu đúng 1 dự án bằng 0,7.
Đúng
Sai
c) Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là 0,75.
Đúng
Sai
d) Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là 0,25.
Đúng
Sai
Đáp án
a) A và B là hai biến cố độc lập.
Đúng
Sai
b) Xác suất để công ty thắng thầu đúng 1 dự án bằng 0,7.
Đúng
Sai
c) Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là 0,75.
Đúng
Sai
d) Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là 0,25.
Đúng
Sai
Phương pháp giải :
a) A và B là hai biến cố độc lập khi P(A).P(B) = P(AB). b) Áp dụng công thức cộng cho nhóm biến cố đầy đủ. c) Áp dụng công thức xác suất của biến cố A với điều kiện B: \(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{P(A \cap B)}}{{P(B)}}\). d) Áp dụng công thức có điều kiện và xác suất của biến cố đối. Lời giải chi tiết :
a) Sai. Có P(A).P(B) = 0,4.0,5 = 0,2. Mà P(AB) = 0,3. Suy ra \(P(A).P(B) \ne P(AB)\). Do đó, hai biến cố A, B không độc lập. b) Sai. Gọi C là biến cố: “Thắng thầu đúng 1 dự án”. Khi đó \(C = \overline A B \cup A\overline B \). Mà \(\overline A B\) và \(A\overline B \) là các biến cố xung khắc nên \(P(C) = P(\overline A B) + P(A\overline B )\). Ta có: \(P(A) = P(A\overline B ) + P(AB) \Leftrightarrow P(A\overline B ) = P(A) - P(AB) = 0,4 - 0,3 = 0,1\). \(P(B) = P(\overline A B) + P(AB) \Leftrightarrow P(\overline A B) = P(B) - P(AB) = 0,5 - 0,3 = 0,2\). Vậy \(P(C) = P(\overline A B) + P(A\overline B ) = 0,2 + 0,1 = 0,3\). c) Đúng. \(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{0,3}}{{0,4}} = 0,75\). d) Sai. \(P(B|\overline A ) = \frac{{P(\overline A B)}}{{P(\overline A )}} = \frac{{P(\overline A B)}}{{1 - P(A)}} = \frac{{0,2}}{{1 - 0,4}} = \frac{1}{3}\).
Câu 4 :
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục toạ độ là kilomet), một máy bay đang ở vị trí A(3,5;2;0,4) và sẽ hạ cánh ở vị trí B(3,5;5,5;0) trên đường băng EG (hình vẽ). a) Đường thẳng AB có phương trình tham số là \(\left\{ \begin{array}{l}x = 3,5\\y = - 2 + 7,5t\\z = 0,4 - 0,4t\end{array} \right.\) \((t \in \mathbb{R})\).
Đúng
Sai
b) Khi máy bay ở vị trí D(3,5;3,25;0,12) thì máy bay cách mặt đất 120 m.
Đúng
Sai
c) Có một lớp mây được mô phỏng bởi một mặt phẳng \((\alpha )\) đi qua ba điểm M(5;0;0), N(0;-5;0), P(0;0;0,5). Vị trí mà máy bay xuyên qua đám mây để hạ cánh là \(C\left( {\frac{7}{2};\frac{{47}}{{44}};\frac{{13}}{{55}}} \right)\).
Đúng
Sai
d) Theo quy định an toàn bay, người phi công phải nhìn thấy điểm đầu E(3,5;4,5;0) của đường băng ở độ cao tối thiểu là 120 m. Nếu sau khi ra khỏi đám mây, tầm nhìn của người phi công là 900 m thì người phi công đã không đạt được quy định an toàn bay. (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
Đúng
Sai
Đáp án
a) Đường thẳng AB có phương trình tham số là \(\left\{ \begin{array}{l}x = 3,5\\y = - 2 + 7,5t\\z = 0,4 - 0,4t\end{array} \right.\) \((t \in \mathbb{R})\).
Đúng
Sai
b) Khi máy bay ở vị trí D(3,5;3,25;0,12) thì máy bay cách mặt đất 120 m.
Đúng
Sai
c) Có một lớp mây được mô phỏng bởi một mặt phẳng \((\alpha )\) đi qua ba điểm M(5;0;0), N(0;-5;0), P(0;0;0,5). Vị trí mà máy bay xuyên qua đám mây để hạ cánh là \(C\left( {\frac{7}{2};\frac{{47}}{{44}};\frac{{13}}{{55}}} \right)\).
Đúng
Sai
d) Theo quy định an toàn bay, người phi công phải nhìn thấy điểm đầu E(3,5;4,5;0) của đường băng ở độ cao tối thiểu là 120 m. Nếu sau khi ra khỏi đám mây, tầm nhìn của người phi công là 900 m thì người phi công đã không đạt được quy định an toàn bay. (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
Đúng
Sai
Phương pháp giải :
a) Đường thẳng đi qua điểm \(M({x_0};{y_0};{z_0})\), nhận vecto \(\overrightarrow u = (a;b;c)\) làm vecto chỉ phương có phương trình tham số là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) \((t \in \mathbb{R})\). b) Tính khoảng cách từ D đến mặt phẳng (Oxy). c) Tìm giao điểm của mặt phẳng (MNP) và đường thẳng AB. d) Tính khoảng cách DE và so sánh với 900 m. Lời giải chi tiết :
a) Đúng. Đường thẳng AB đi qua điểm \(A\left( {3,5; - 2;0,4} \right)\) và nhận \(\overrightarrow {AB} {\rm{\;}} = \left( {0;7,5; - 0,4} \right)\) làm một vectơ chỉ phương nên phương trình tham số của đường thẳng AB là: \(\left\{ {\begin{array}{*{20}{l}}{x = 3,5}\\{y = {\rm{\;}} - 2 + 7,5t}\\{z = 0,4 - 0,4t}\end{array}} \right.\) (t là tham số). b) Đúng. Điểm D có cao độ là 0,12, suy ra khoảng cách từ D đến mặt đất (Oxy) là 0,12 km = 120 m. c) Sai. Phương trình mặt chắn của mặt phẳng (MNP) là: \(\frac{x}{5} + \frac{y}{{ - 5}} + \frac{z}{{0,5}} = 1\). Từ đó, ta suy ra phương trình tổng quát của (MNP) là: \(x - y + 10z - 5 = 0\). Vì C là vị trí mà máy bay xuyên qua đám mấy để hạ cánh nên C là giao điểm của đường thẳng AB và mặt phẳng \(\left( {\alpha {\rm{\;}}} \right)\). Vì C thuộc AB nên \(C\left( {3,5; - 2 + 7,5t;0,4 - 0,4t} \right)\). Mà C thuộc mặt phẳng \(\left( {\alpha {\rm{\;}}} \right)\) nên: \(3,5 - \left( { - 2 + 7,5t} \right) + 10\left( {0,4 - 0,4t} \right) - 5 = 0\), suy ra \(t = \frac{9}{{23}}\). Do đó, \(C\left( {\frac{7}{2};\frac{{43}}{{46}};\frac{{28}}{{115}}} \right)\). d) Đúng. Khi máy bay cách mặt đất 120 m, nó đang ở vị trí điểm D. DE là tầm nhìn của phi công tới E khi cách mặt đất 120 m. Ta có: \(DE = \sqrt {{{\left( {3,5 - 3,5} \right)}^2} + {{\left( {4,5 - 3,25} \right)}^2} + {{\left( {0 - 0,12} \right)}^2}} {\rm{\;}} \approx 1,256\) (km). Vì tầm nhìn của phi công sau khi ra khỏi đám mây là \(900m = 0,9km < 1,256km\) nên người phi công đó không nhìn thấy E, do đó không đạt được quy định an toàn bay.
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Cho tứ diện đều ABCD có cạnh bằng 2. Khoảng cách giữa hai đường thẳng AB và CD bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tìm đoạn vuông góc chung của AB và CD. Lời giải chi tiết :
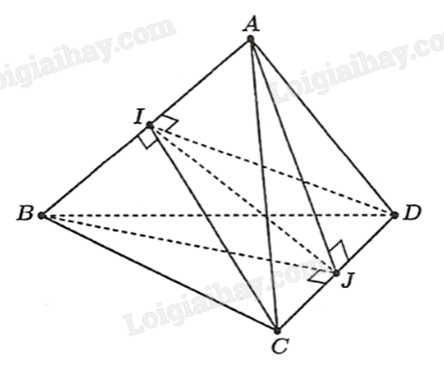
Gọi I, J theo thứ tự là trung điểm của AB, CD. Các tam giác đều ABC, ABD có I là trung điểm của AB nên \(\left\{ \begin{array}{l}AB \bot CI\\AB \bot DI\end{array} \right.\), suy ra \(AB \bot (ICD)\), mà \(IJ \subset (ICD)\) nên \(AB \bot IJ\) (1). Tương tự, các tam giác đều ACD, BCD có J là trung điểm của CD nên \(\left\{ \begin{array}{l}CD \bot AJ\\CD \bot BJ\end{array} \right.\), suy ra \(CD \bot (ABJ)\), mà \(IJ \subset (ABJ)\) nên \(CD \bot IJ\) (2). Từ (1) và (2) suy ra IJ là đoạn vuông góc chung của hai đường thẳng AB, CD. Vậy, IJ là khoảng cách giữa hai đường thẳng AB, CD. CI là đường cao tam giác đều ABC cạnh 2 nên \(CI = \frac{{2\sqrt 3 }}{2} = \sqrt 3 \). Sử dụng định lý Pythagore cho tam giác CIJ vuông tại J, ta có: \(IJ = \sqrt {C{I^2} - C{J^2}} = \sqrt {3 - 1} = \sqrt 2 \approx 1,41\).
Câu 2 :
Một công ty vận tải cần giao hàng đến tất cả các thành phố A, B, C, D, E (hình vẽ bên dưới). Chi phí di chuyển giữa các thành phố được mô tả trên hình. Xe giao hàng của công ty xuất phát từ một thành phố trong năm thành phố trên đi qua tất cả các thành phố còn lại đúng một lần sau đó trở lại thành phố ban đầu. Tìm chi phí thấp nhất của xe giao hàng.
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Liệt kê và so sánh. Lời giải chi tiết :
Do đó, chi phí nhỏ nhất của xe giao hàng là 53.
Câu 3 :
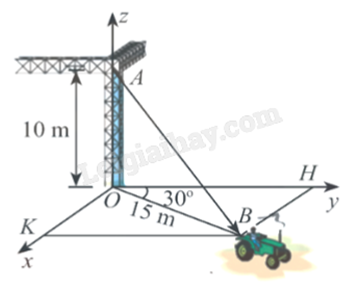
Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ tọa độ Oxyz như hình vẽ với độ dài đơn vị trên các trục tọa độ bằng 1 m. Biết . Tính x + 2y – z (làm tròn kết quả đến hàng phần mười).
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng hệ thức lượng giác và định lý Pythagore để tính tọa độ điểm B. Từ đó tìm tọa độ \(\overrightarrow {AB} = (x;y;z)\). Lời giải chi tiết :
A(0;0;10). \(\sin \widehat {HOB} = \frac{{BH}}{{OB}} \Leftrightarrow \sin {30^o} = \frac{{BH}}{{OB}} \Leftrightarrow BH = OB\sin {30^o} = 15\sin {30^o} = \frac{{15}}{2}\). Suy ra \({x_B} = OK = BH = 7,5\). \({y_B} = OH = \sqrt {O{B^2} - B{H^2}} = \sqrt {{{15}^2} - {{\left( {\frac{{15}}{2}} \right)}^2}} = \frac{{15\sqrt 3 }}{2}\). B thuộc mặt phẳng (Oxy) nên \({z_B} = 0\). \(\overrightarrow {AB} = \left( {\frac{{15}}{2};\frac{{15\sqrt 3 }}{2}; - 10} \right)\). Vậy \(x + 2y - z = \frac{{15}}{2} + 2.\frac{{15\sqrt 3 }}{2} - ( - 10) \approx 43,5\).
Câu 4 :
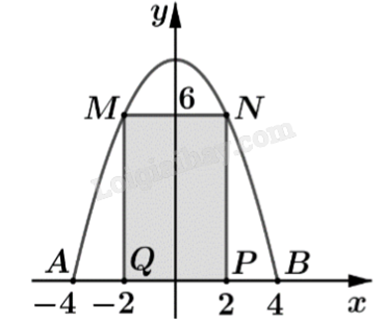
Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là AB = 8 m. Người treo một tấm phông hình chữ nhật có hai đỉnh M, N nằm trên Parabol và hai đỉnh P, Q nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta mua hoa để trang trí hoa, biết MN = 4 m, MQ = 6 m. Diện tích phần phía ngoài phông để trang trí hoa (phần không tô đen) là bao nhiêu mét vuông (kết quả làm tròn đến hàng phần mười)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tính diện tích phần phía ngoài phông để trang trí hoa bằng cách tính diện khoảng trống giới hạn bởi cổng parabol với mặt đất rồi trừ đi diện tích tấm phông chữ nhật MNPQ. + Chọn hệ trục tọa độ phù hợp, xác định tọa độ các điểm. + Ứng dụng hình học của tích phân tính diện tích. Lời giải chi tiết :
Gọi \({S_P}\) là diện tích khoảng trống giới hạn bởi cổng parabol với mặt đất, \({S_{MNPQ}}\) là diện tích tấm phông hình chữ nhật MNPQ, S là diện tích phần ngoài phông cần tính. Khi đó, \(S = {S_P} - {S_{MNPQ}} = {S_P} - MN.MQ = {S_P} - 4.6 = {S_P} - 24\). Chọn hệ trục tọa độ như hình vẽ:
Gọi đồ thị cổng parabol có phương trình là \(y = a{x^2} + bx + c\). Vì parabol đi qua các điểm có tọa độ (4;0), (-4;0) và (2;6) nên ta có hệ phương trình: \(\left\{ \begin{array}{l}0 = a{.4^2} + b.4 + c\\0 = a.{( - 4)^2} + b.( - 4) + c\\6 = a{.2^2} + b.2 + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{2}\\b = 0\\c = 8\end{array} \right. \Rightarrow \) Đồ thị cổng parabol có phương trình là \(y = - \frac{1}{2}{x^2} + 8\). \({S_P}\) là phần hình phẳng giới hạn bởi parabol \(y = - \frac{1}{2}{x^2} + 8\) và trục hoành nên: \({S_P} = \int\limits_{ - 4}^4 {\left| { - \frac{1}{2}{x^2} + 8} \right|dx} = \int\limits_{ - 4}^4 {\left( { - \frac{1}{2}{x^2} + 8} \right)dx} = \frac{{128}}{3}\) \(({m^2})\). Vậy diện tích phía ngoài phông để trang trí hoa là \(S = {S_P} - 24 = \frac{{128}}{3} - 24 = \frac{{56}}{3} \approx 18,7\) \(({m^2})\).
Câu 5 :
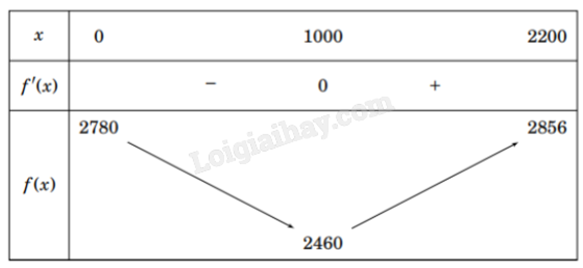
Có hai xã A, B cùng ở một bên bờ sông. Khoảng cách từ hai xã đó đến bờ sông lần lượt là AA′ = 500 m, BB′ = 600 m. Người ta đo được A’B’ = 2200 m như hình vẽ dưới đây. Các kỹ sư muốn xây dựng một trạm cung cấp nước sạch nằm bên bờ sông cho người dân của hai xã sử dụng. Để tiết kiệm chi phí, các kỹ sư phải chọn một vị trí M của trạm cung cấp nước sạch đó trên đoạn A’B’ sao cho tổng khoảng cách từ hai xã đến vị trí M là nhỏ nhất. Giá trị nhỏ nhất của tổng khoảng cách đó bằng bao nhiêu mét (làm tròn đến hàng đơn vị)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Lập hàm số tính khoảng cách AM + MB. Tìm giá trị nhỏ nhất của hàm số vừa tìm được bằng cách ứng dụng đạo hàm. Lời giải chi tiết :
Đặt A’M = x (0 < x < 2200), B’M = 2200 – x (m). Ta có \(AM = \sqrt {{x^2} + {{500}^2}} \), \(BM = \sqrt {{{(2200 - x)}^2} + {{600}^2}} \) (m). Tổng khoảng cách từ hai xã đến vị trí M là: \(AM + BM = \sqrt {{x^2} + {{500}^2}} + \sqrt {{{(2200 - x)}^2} + {{600}^2}} \) (m). Xét hàm số \(f(x) = \sqrt {{x^2} + {{500}^2}} + \sqrt {{{(2200 - x)}^2} + {{600}^2}} \) (m). Đạo hàm \(f'(x) = \frac{x}{{\sqrt {{x^2} + {{500}^2}} }} + \frac{x}{{\sqrt {{{(2200 - x)}^2} + {{600}^2}} }} = 0 \Leftrightarrow x = 1000\) (m). Bảng biến thiên:
Giá trị nhỏ nhất của tổng khoảng cách từ hai xã đó đến bờ sông là khoảng 2460 m, tại vị trí M cách điểm A’ là 1000 m.
Câu 6 :
Một căn bệnh có 1% dân số mắc phải. Một phương pháp chuẩn đoán được phát triển có tỷ lệ chính xác là 99%. Với những người bị bệnh, phương pháp này sẽ đưa ra kết quả dương tính 99% số trường hợp. Với người không mắc bệnh, phương pháp này cũng chuẩn đoán đúng 99 trong 100 trường hợp. Nếu một người kiểm tra và kết quả là dương tính (bị bệnh), xác suất để người đó thực sự bị bệnh là bao nhiêu (kết quả viết dưới dạng số thập phân)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng công thức xác suất có điều kiện và công thức Bayes. Lời giải chi tiết :
A: “Người đó mắc bệnh”. Căn bệnh có 1% dân số mắc phải nên P(A) = 1% = 0,01. \(\overline A \): “Người đó không mắc bệnh”. \(P(\overline A ) = 1 - P(A) = 0,99\). B: “Kết quả kiểm tra của người đó là dương tính”. Xác suất kết quả dương tính nếu người đó mắc bệnh là P(B|A) = 99% = 0,99. Xác suất kết quả dương tính nếu người đó không mắc bệnh là \(P(B|\overline A ) = 1 - P(B|A) = 1 - 0,99 = 0,01\). Áp dụng công thức Bayes, xác suất để một người kiểm tra dương tính mà thực sự bị bệnh là: \(P(A|B) = \frac{{P(A).P(B|A)}}{{P(A).(B|A) + P(\overline A ).(B|\overline A )}} = \frac{{0,01.0,99}}{{0,01.0,99 + 0,99.0,01}} = 0,5\). |