Đề số 5 - Đề kiểm tra học kì 2 - Toán 7

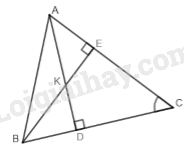
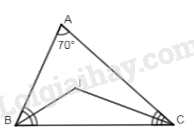
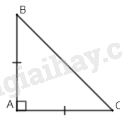
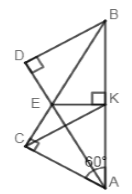
Đề bài

I. TRẮC NGHIỆM (2 điểm)

Câu 1: Thu gọn đơn thức $- {x^3}{\left( {xy} \right)^4}\dfrac{1}{3}{x^2}{y^3}{z^3}$ kết quả là:

A. $\dfrac{1}{3}{x^6}{y^8}{z^3}$               B.$\dfrac{1}{3}{x^9}{y^5}{z^4}$    

C. $- 3{{\rm{x}}^8}{y^4}{z^3}$                  D.$\dfrac{{ - 1}}{3}{x^9}{y^7}{z^3}$

Câu 2: Đơn thức thích hợp điền vào chỗ chấm trong phép toán: $3{x^3} + ... =  - 3{x^3}$ là:

A. $3{x^3}$                B. $- 6{x^3}$  

C.$0$                                      D. $6{x^3}$

Câu 3 Cho các đa thức $A = 3{x^2} - 7xy - \dfrac{3}{4};\,B =  - 0,75 + 2{x^2} + 7xy$. Đa thức $C$ thỏa mãn $C + B = A$  là:

A.$C = 14xy - {x^2}$                        B. $C = {x^2}$ 

C.$C = 5{x^2} - 14xy$                      D.${x^2} - 14xy$  

Câu 4: Cho hai đa thức $P\left( x \right) =  - {x^3} + 2{x^2} + x - 1$   và $Q\left( x \right) = {x^3} - {x^2} - x + 2$  nghiệm của đa thức $P\left( x \right) + Q\left( x \right)$ là:

A. Vô nghiệm                         B. $- 1$    

C. $1$                                                 D. $0$

Câu 5: Cho tam giác nhọn $ABC,\,\angle C = {50^0}$ các đường cao $A{\rm{D}},\,BE$ cắt nhau tại $K$. Câu nào sau đây sai?

A. $\angle AKB = {130^0}$                         B. $\angle KBC = {40^0}$              

C. $\angle A > \angle B > \angle C$                                    D. $\angle K{\rm{A}}C = \angle EBC$

Câu 6: Cho tam giác $ABC$ có $\angle A = {70^0}$. Gọi $I$ là giao điểm các tia phân giác $\angle B$ và $\angle C$. Số đo $\angle BIC$ là:

A. ${135^0}$                         B. ${115^0}$

C. ${125^0}$                         D. ${105^0}$

Câu 7: Cho $\Delta ABC$ có $\angle C = {50^0},\,\angle B = {60^0}$. Câu nào sau đây đúng:

A. $AB > AC > BC$                        

B. $AB > BC > AC$                        

C. $BC > AC > AB$            

D. $AC > BC > AB$

Câu 8: Cho $\Delta ABC$ có $AB = AC$ có $\angle A = 2\angle B$ có dạng đặc biệt nào:

A. Tam giác vuông                 

B. Tam giác đều                     

C. Tam giác cân                     

D. Tam giác vuông cân

II. TỰ LUẬN (8 điểm)

Bài 1 (1,5 điểm) Cho đa thức: $7{x^3} + 3{x^4} - x + 5{x^2}$$- 6{x^3} - 2{x^4} + 2018 + {x^3}$

a) Thu gọn và sắp xếp đa thức theo lũy thừa giảm của biến.

b) Chỉ rõ hệ số cao nhất và hệ số tự do của đa thức.

Bài 2 (2,5 điểm) Cho 2 đa thức $P\left( x \right) = {x^2} + 2x - 5$ và $Q\left( x \right) = {x^2} - 9x + 5$

a) Tính $M\left( x \right) = P\left( x \right) + Q\left( x \right);\,$$N\left( x \right) = P\left( x \right) - Q\left( x \right)$  

b) Tìm nghiệm các đa thức $M\left( x \right);\,N\left( x \right)$ 

c) Không đặt phép tính tìm đa thức $Q\left( x \right) - P\left( x \right)$

Bài 3 (3,5 điểm) Cho $\Delta ABC$ vuông tại $C$ có $\angle A = {60^0}$. Tia phân giác $\angle BAC$ cắt $BC$ ở $E$. Kẻ $EK$ vuông góc với $AB$ ở $K$. Kẻ $BD$ vuông góc với $AE$ ở $D$.

a) Chứng minh: $AC = AK$   và $CK \bot AE$  

b) Chứng minh: $AB = 2AC$  

c) Chứng minh:$EB > AC$ 

d) Chứng minh: $AC,\,EK,\,BD$ là ba đường đồng quy.

Bài 4 (0,5 điểm) Cho đa thức $f\left( x \right) = a{x^2} + bx + c$. Tính giá trị của $f\left( { - 1} \right)$ biết $a + c = b + 2018$.

Đ/a TN

Câu 1:

Phương pháp: Áp dụng quy tắc nhân đơn thức: Để nhân hai đơn thức ta nhân các hệ số với nhau và nhân các phần biến với nhau.

Cách giải:

$\begin{array}{l} - {x^3}{\left( {xy} \right)^4}\dfrac{1}{3}{x^2}{y^3}{z^3}\\ =  - \dfrac{1}{3}{x^5}.{x^4}.{y^4}.{y^3}.{z^3}\\ =  - \dfrac{1}{3}{x^9}.{y^7}.{z^3}\end{array}$

Chọn D

Câu 2:

Phương pháp: Để cộng (hay trừ)  các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến.

Cách giải:

Đơn thức cần điền vào dấu ba chấm là:

$- 3{x^3} - 3{x^3}$$= \left( { - 3 - 3} \right){x^3} =  - 6{x^3}$

Chọn B                                     

Câu 3:

Phương pháp: Áp dụng quy tắc cộng, trừ hai  đa thức: Muốn cộng, trừ hai đa thức, ta thực hiện nhóm các hạng tử đồng dạng rồi cộng các đơn thức đồng dạng với nhau.

Cách giải:

$C + B = A$$\Rightarrow C = A - \,B$$= 3{x^2} - 7xy - \dfrac{3}{4}$$- \left( { - 0,75 + 2{x^2} + 7xy} \right)$

$= 3{x^2} - 7xy - \dfrac{3}{4} + 0,75$$- 2{x^2} - 7xy$$= {x^2} - 14xy$

Chọn D

Câu 4:

Phương pháp: Áp dụng quy tắc cộng, trừ hai đa thức. Giải $P\left( x \right) + Q\left( x \right) = 0$để tìm nghiệm của đa thức đó.

+ Muốn cộng, trừ hai đa thức, ta thực hiện nhóm các hạng tử đồng dạng rồi cộng các đơn thức đồng dạng với nhau.

+ Nghiệm của đa thức một biến: Nếu tại $x = a$ đa thức $P\left( x \right)$ có giá trị bằng 0 thì ta nói a {hoặc $x = a$ } là một nghiệm của đa thức đó.

Cách giải:

$P\left( x \right) + Q\left( x \right)$$=  - {x^3} + 2{x^2} + x - 1$$+ {x^3} - {x^2} - x + 2$$= {x^2} + 1$

$\begin{array}{l}P\left( x \right) + Q\left( x \right) = 0\\ \Leftrightarrow {x^2} + 1 = 0\end{array}$

$\Leftrightarrow {x^2} =  - 1\,\,$ (Vô nghiệm) (Vì ${x^2} \ge 0\,$ với mọi $x$)

Chọn A

Câu 5:

Phương pháp: Áp dụng tính chất trong tam giác vuông hai góc nhọn phụ nhau, tính chất hai góc kề bù.

Cách giải:

Xét ${\Delta _v}BEC$ có:

$\begin{array}{l}\angle E = {90^0} \Rightarrow \angle C + \angle EBC = {90^0}\\ \Rightarrow \angle EBC = {90^0} - \angle C\\ = {90^0} - {50^0} = {40^0}\end{array}$

nên kết luận của đáp án B đúng.

Xét ${\Delta _v}BKD$ có:

$\begin{array}{l}\angle D = {90^0}\\ \Rightarrow \angle KBD + \angle BKD = {90^0}\\ \Rightarrow \angle BKD = {90^0} - \angle KBD\\ = {90^0} - {40^0} = {50^0}\end{array}$

Mà $\angle BKD + \angle BKA = {180^0}$$\Rightarrow \angle BKA = {180^0} - \angle BKD$$= {180^0} - {50^0} = {130^0}$  nên kết luận của đáp án A đúng.

Xét ${\Delta _v}ADC$ có:

$\begin{array}{l}\angle D = {90^0}\\ \Rightarrow \angle DAC + \angle C = {90^0}\\ \Rightarrow \angle DAC = {90^0} - \angle C\\ = {90^0} - {50^0} = {40^0}\\ \Rightarrow \angle K{\rm{A}}C = \angle EBC\end{array}$

Nên kết luận của đáp án D đúng.

Vậy kết luận của đáp án C sai.

Chọn C

Câu 6:

Phương pháp: Áp dụng tính chất tia phân giác và định lý tổng ba góc của tam giác.

Cách giải:

Vì $BI$ và $CI$ là tia phân giác của $\angle ABC$ và $\angle ACB\,\,\left( {gt} \right)$

$\Rightarrow \left\{ \begin{array}{l}\angle IBC = \dfrac{1}{2}\angle ABC\\\angle ICB = \dfrac{1}{2}\angle ACB\end{array} \right.$    (tính chất tia phân giác)

$\begin{array}{l} \Rightarrow \angle IBC + \angle ICB\\ = \dfrac{1}{2}\left( {\angle ABC + \angle ACB} \right)\\ = \dfrac{1}{2}\left( {{{180}^0} - \angle A} \right)\\ = \dfrac{1}{2}\left( {{{180}^0} - {{70}^0}} \right)\\ = \dfrac{1}{2}{.110^0} = {55^0}\end{array}$

Xét $\Delta BIC$ có: $\angle BIC + \angle IBC + \angle ICB = {180^0}$ (tổng ba góc trong tam giác)

$\Rightarrow \angle BIC = {180^0} - \left( {\angle IBC + \angle ICB} \right)$ $= {180^0} - {55^0} = {125^0}$

Chọn C

Câu 7:

Phương pháp: Áp dụng định lý tổng ba góc của một tam giác và bất đẳng thức trong tam giác.

Cách giải: Xét $\Delta ABC$ có: $\angle A + \angle B + \angle C = {180^0}$ (định lý tổng ba góc trong tam giác)

 $\Rightarrow \angle A = {180^0} - \angle B - \angle C$$= {180^0} - {50^0} - {60^0} = {70^0}$

Vì $\angle C < \angle B < \angle A\,\,\left( {{{50}^0} < {{60}^0} < {{70}^0}} \right)$$\Rightarrow AB < AC < BC$ (bất đẳng thức tam giác)

Chọn C.

Câu 8:

Phương pháp: Áp dụng định lý tổng ba góc trong tam giác, tính chất tam giác cân, dấu hiệu nhận biết tam giác vuông cân.

Cách giải:

Vì $AB = AC\,\left( {gt} \right) \Rightarrow \Delta ABC$ cân tại $A$ (dấu hiệu nhận biết tam giác cân)

$\Rightarrow \angle B = \angle C$ (tính chất tam giác cân) 

Ta có: $\angle A + \angle B + \angle C = {180^0}$ (định lý tổng ba góc của tam giác)

Mà

$\begin{array}{l}\left\{ \begin{array}{l}\angle B = \angle C\\\angle A = 2\angle B\\\angle A + \angle B + \angle C = {180^0}\end{array} \right.\\ \Rightarrow 2\angle B + 2\angle C = {180^0}\end{array}$

$\begin{array}{l} \Rightarrow \angle B + \angle C = {180^0}:2 = {90^0}\\ \Rightarrow \angle A = {180^0} - {90^0} = {90^0}\end{array}$

$\Rightarrow \Delta ABC$ là tam giác vuông cân tại $A$ (dấu hiệu nhận biết tam giác vuông cân)

Chọn D

LG bài 1

Phương pháp giải:

Áp dụng quy tắc cộng, trừ đa thức: Muốn cộng, trừ hai đa thức, ta thực hiện nhóm các hạng tử đồng dạng rồi cộng các đơn thức đồng dạng với nhau.

Để cộng hoặc trừ hai đa thức một biến ta có thể thực hiện theo một trong hai cách sau:

Cách 1: Thực hiện nhóm các hạng tử đồng dạng rồi cộng các đơn thức đồng dạng với nhau.

Cách 2: Sắp xếp các hạng tử của hai đa thức cùng theo lũy thừa giảm hoặc tăng của biến, rồi đặt phép tính theo cột dọc tương tự như cộng, trừ các số (chú ý đặt các đơn thức đồng dạng ở cùng một cột).

Lời giải chi tiết:

a) $7{x^3} + 3{x^4} - x + 5{x^2}$$- 6{x^3} - 2{x^4} + 2018 + {x^3}$

$= 3{x^4} - 2{x^4} + 7{x^3} - 6{x^3}$$+ {x^3} - x + 2018$

$= {x^4} + 2{x^3} - x + 2018$

b) Hệ số cao nhất là: $1$, hệ số tự do là $2018$.

LG bài 2

Phương pháp giải:

Áp dụng quy tắc cộng, trừ đa thức. Muốn tìm nghiệm của đa thức ta cho đa thức đó bằng $0$ và giải tìm nghiệm.

Lời giải chi tiết:

$\begin{array}{l}a)\,M\left( x \right) = P\left( x \right) + Q\left( x \right)\\ = {x^2} + 2x - 5 + {x^2} - 9x + 5\\ = 2{x^2} - 7x\\N\left( x \right) = P\left( x \right) - Q\left( x \right)\\ = {x^2} + 2x - 5 - \left( {{x^2} - 9x + 5} \right)\\ = {x^2} + 2x - 5 - {x^2} + 9x - 5\\ = 11x - 10\end{array}$

$\begin{array}{l}b)\,M\left( x \right) = 0\\ \Leftrightarrow 2{x^2} - 7x = 0\\ \Leftrightarrow x\left( {2x - 7} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\2x - 7 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{7}{2}\end{array} \right.\\N\left( x \right) = 0\\ \Leftrightarrow 11x - 10 = 0\\ \Leftrightarrow x = \dfrac{{10}}{{11}}\end{array}$

c)  Ta có: $\begin{array}{l}Q\left( x \right) - P\left( x \right)\\ =  - \left( {Q\left( x \right) - P\left( x \right)} \right)\\ =  - N\left( x \right) =  - 11x + 10\end{array}$

LG bài 3

Phương pháp giải:

Áp dụng dấu hiệu nhận biết đường trung trực của đoạn thẳng, tính chất tam giác cân, tính chất tia phân giác, bất đẳng thức tam giác, tính chất ba đường cao trong tam giác.

Lời giải chi tiết:

a)  Vì $AE$ là phân giác của $\angle CAK\,\left( {gt} \right)$ $\Rightarrow \angle CAE = \angle BAE$ (tính chất tia phân giác)

Xét ${\Delta _v}ACE$ và ${\Delta _v}AKE$ có:

$AE$ chung (gt)

$\angle CAE = \angle BAE\,\left( {cmt} \right)$

$\Rightarrow {\Delta _v}ACE = {\Delta _v}AKE$ (cạnh huyền – góc nhọn)

$\Rightarrow AC = AK$ (hai cạnh tương ứng)

Vì ${\Delta _v}ACE = {\Delta _v}AKE\,\left( {cmt} \right)\,$$\Rightarrow \,\,CE = \,EK$ (hai cạnh tương ứng) (1)

Vì $AC = AK\,\,\left( {cmt} \right)$ (2)

Từ (1) và (2) suy ra $AE$ là đường trung trực của $CK$ (dấu hiệu nhận biết đường trung trực của đoạn thẳng)

$\Rightarrow CK \bot \,\,AE$ (tính chất đường trung trực của đoạn thẳng)

b) Xét ${\Delta _v}ABC$ có $\angle B + \angle BAC = {90^0}$ $\Rightarrow \angle B = {90^0} - \angle BAC$$= {90^0} - {60^0} = {30^0}$

Vì $AE$ là phân giác của $\angle BAC\,\,\left( {gt} \right)\,$$\Rightarrow \angle EBA\, = \dfrac{1}{2}\angle BAC$$= \dfrac{1}{2}{.60^0} = {30^0}$ (tính chất tia phân giác)

$\Rightarrow \angle EBA\,\, = \,\angle EAB\, = {30^0}$$\Rightarrow \Delta ABE$ cân tại $E$ (dấu hiệu nhận biết tam giác cân)

Mà $EK \bot AB\,\left( {gt} \right) \Rightarrow EK$ cũng là đường trung trực của $AB$ (tính chất tam giác cân)

$\Rightarrow AB = 2AK$ (tính chất đường trung trực)

Mà $AK = AC\,\left( {cmt} \right)\,$ $\Rightarrow AB = 2AC$

c) Xét ${\Delta _v}BEK$ có: $EB > BK$ (bất đẳng thức tam giác)

Mà $\left\{ \begin{array}{l}BK = AK\\AK = AC\end{array} \right.\,\,\left( {cmt} \right)$ $\Rightarrow EB > AC$

d) Xét $\Delta ABE$ có:

$\left\{ \begin{array}{l}BD\, \bot \,AE\\EK\, \bot \,AB\\AC\, \bot \,BE\,\end{array} \right.\,\,\left( {gt} \right)$ 

Suy ra $BD,\,EK,\,\,AC$ là ba đường cao của $\Delta ABE$, 

Mà trong một tam giác ba đường cao đồng quy tại một điểm. Vậy 3 đường thẳng $BD,\,EK,\,\,AC$ đồng quy.

LG bài 4

Phương pháp giải:

Tính $f\left( { - 1} \right)$bằng cách thay $x =  - 1$ vào $f\left( x \right) = a{x^2} + bx + c$. Sau đó, thay $a + c = b + 2018$  vào $f\left( { - 1} \right)$.

Lời giải chi tiết:

Ta có:

 $f\left( { - 1} \right) = a.{\left( { - 1} \right)^2} + b.\left( { - 1} \right) + c$ $= \,a - b + c = \,\left( {a + c} \right) - b$

Mà $a + c = b + 2018$$\Rightarrow f\left( { - 1} \right) = b + 2018 - b = 2018$. Vậy $f\left( { - 1} \right) = 2018$

Nguồn sưu tầm

HocTot.Nam.Name.Vn