Đề số 3 - Đề kiểm tra học kì 2 - Toán 7Đáp án và lời giải chi tiết Đề số 3 - Đề kiểm tra học kì 2 - Toán 7
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài Câu 1 (1,5 điểm). Điểm kiểm tra học kì 1 môn Toán của tất cả học sinh trong lớp 7A được ghi lại như sau:
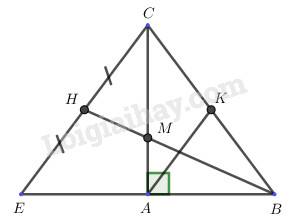
a) Dấu hiệu ở đây là gì? Số các giá trị của dấu hiệu là bao nhiêu? b) Lập bảng tần số và tính số trung bình cộng của dấu hiệu. Câu 2 (2,0 điểm). a) Cho đơn thức \(A = \left( { - \dfrac{1}{2}x{y^2}} \right).{\left( {2{x^3}y} \right)^2}\). Thu gọn và tính giá trị của \(A\) khi \(x = - 1\) và \(y = \dfrac{1}{2}\). b) Tìm hệ số \(a\) của đa thức \(P\left( x \right) = a\,{x^2} + 2x + 1\) biết rằng \(P\left( {\dfrac{1}{2}} \right) = 1\). Câu 3 (2,5 điểm). Cho các đa thức: \(F\left( x \right) = 5{x^2} - 1 + 3x + {x^2} - 5{x^3}\) và \(G\left( x \right) = 2 - 3{x^3} + 6{x^2} + 5x - 2{x^3} - x.\) a) Thu gọn và sắp xếp hai đa thức \(F\left( x \right)\) và \(G\left( x \right)\) theo lũy thừa giảm dần của biến. b) Tính \(M\left( x \right) = F\left( x \right) - G\left( x \right)\); Tìm nghiệm của đa thức \(M\left( x \right)\) c) Tìm đa thức \(N\left( x \right)\) biết \(N\left( x \right) + F\left( x \right) = - G\left( x \right)\) Câu 4 (3,5 điểm). Cho \(\Delta ABC\) vuông tại \(A\) , có \(AB = 9cm,\,BC = 15cm.\) Trên tia đối của tia \(AB\) lấy điểm \(E\) sao cho \(A\) là trung điểm của \(BE.\) a) Tính độ dài cạnh \(AC\) và so sánh các góc của tam giác \(ABC\). b) Chứng minh rằng hai tam giác \(ABC\) và tam giác \(AEC\) bằng nhau. c) Vẽ đường trung tuyến \(BH\) của tam giác \(BEC\) cắt cạnh \(AC\) tại \(M.\) Chứng minh \(M\) là trọng tâm của tam giác \(BEC\) và tính độ dài đoạn \(CM.\) d) Từ \(A\) vẽ đường thẳng song song với \(EC\), đường thẳng này cắt cạnh \(BC\) tại \(K\). Chứng minh rằng ba điểm \(E,M,K\) thẳng hàng. Câu 5 (0,5 điểm). Cho đa thức \(f\left( x \right) = a\,{x^3} + b{x^2} + cx + d\) với \(a\) là số nguyên dương và \(f\left( 5 \right) - f\left( 4 \right) = 2019\). Chứng minh \(f\left( 7 \right) - f\left( 2 \right)\) là hợp số. LG câu 1 Phương pháp giải: a) Nêu dấu hiệu. Lưu ý: Dấu hiệu là vấn đề hay hiện tượng mà người điều tra quan tâm tìm hiểu. Chỉ ra số các giá trị của dấu hiệu. b) Tính trung bình cộng. Ta có công thức: \(\overline X = \dfrac{{{x_1}.{n_1} + {x_2}.{n_2} + {x_3}.{n_3} + ... + {x_k}.{n_k}}}{N}\) Trong đó: \({x_1};{x_2};.....;{x_k}\) là \(k\) giá trị khác nhau của dấu hiệu \(X.\) \({n_1};{n_2};....;{n_k}\) là tần số tương ứng. \(N\) là số các giá trị. \(\overline X \) là số trung bình của dấu hiệu \(X.\) Lời giải chi tiết: a) Dấu hiệu: Điểm kiểm tra học kì 1 môn toán của mỗi bạn học sinh trong lớp 7A. Số các giá trị của dấu hiệu là: 30. b) Bảng tần số: Trung bình cộng của dấu hiệu là: \(\overline X \)\(= \dfrac{{3.1 + 4.1 + 5.3 + 6.4 + 7.9 + 8.6 + 9.4 + 10.2}}{{30}}\)\( = 7,1\) (điểm) LG câu 2 Phương pháp giải: a) Thu gọn đơn thức, ta nhân hệ số với nhau và nhân phần biến với nhau. Tính các giá trị của biểu thức ta thay \(x = - 1\) và \(y = \dfrac{1}{2}\) vào biểu thức thu gọn của \(A\). b) Để tìm hệ số \(a\) của đa thức ta thay \(x = \dfrac{1}{2}\) và \(P\left( {\dfrac{1}{2}} \right) = 1\) vào biểu thức của \(P\left( x \right)\). Tính toán và tìm ra kết quả. Lời giải chi tiết: a) Cho đơn thức \(A = \left( { - \dfrac{1}{2}x{y^2}} \right).{\left( {2{x^3}y} \right)^2}\). Thu gọn và tính giá trị của \(A\) khi \(x = - 1\) và \(y = \dfrac{1}{2}\). Ta có: \(\begin{array}{l}A = \left( { - \dfrac{1}{2}x{y^2}} \right).{\left( {2{x^3}y} \right)^2}\\ = \left( { - \dfrac{1}{2}{{.2}^2}} \right).x.{\left( {{x^3}} \right)^2}.{y^2}.{y^2}\\ = - 2.{x^7}.{y^4}\end{array}\) Thay \(x = - 1\) và \(y = \dfrac{1}{2}\) thì \(A = - 2.{\left( { - 1} \right)^7}.{\left( {\dfrac{1}{2}} \right)^4}\)\( = \dfrac{{ - 2.\left( { - 1} \right).1}}{{{2^4}}} = \dfrac{1}{8}\) Vậy \(A = \dfrac{1}{8}\) khi \(x = - 1\) và \(y = \dfrac{1}{2}\). b) Tìm hệ số \(a\) của đa thức \(P\left( x \right) = a\,{x^2} + 2x + 1\) biết rằng \(P\left( {\dfrac{1}{2}} \right) = 1\). Ta có: \(\begin{array}{l}P\left( {\dfrac{1}{2}} \right) = 1\\ \Leftrightarrow a.{\left( {\dfrac{1}{2}} \right)^2} + 2.\dfrac{1}{2} + 1 = 1\\ \Leftrightarrow \,\dfrac{a}{4} + 2 = 1\\ \Leftrightarrow \dfrac{a}{4} = - 1\\ \Leftrightarrow a = - 4\end{array}\) Vậy \(a = - 4\) , đa thức \(P\) có dạng: \(P\left( x \right) = - 4{x^2} + 2x + 1\). LG câu 3 Phương pháp giải: a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến của hai đa thức \(F\left( x \right)\) và \(G\left( x \right)\). Khi thu gọn các đơn thức đồng dạng ta cộng hệ số với nhau và giữ nguyên phần biến, sau đó sắp xếp theo lũy thừa giảm dần của biến số. b) Tính \(M\left( x \right) = F\left( x \right) - G\left( x \right)\). Ta thực hiện trừ hai đa thức. Sau đó tìm nghiệm của đa thức \(M\left( x \right)\), ta cho \(M\left( x \right) = 0\) để tìm nghiệm. c) Biến đổi \(N\left( x \right) + F\left( x \right) = - G\left( x \right)\)\( \Rightarrow N\left( x \right) = - F\left( x \right) - G\left( x \right)\), rồi thực hiện tính. Chú ý: Trước dấu trừ các hạng tử đổi dấu. Lời giải chi tiết: a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến. Thu gọn \(F\left( x \right):\) \(\begin{array}{l}F\left( x \right) = 5{x^2} - 1 + 3x + {x^2} - 5{x^3}\\ = - 5{x^3} + \left( {5{x^2} + {x^2}} \right) + 3x - 1\\ = - 5{x^3} + 6{x^2} + 3x - 1\end{array}\) Thu gọn \(G\left( x \right):\) \(\begin{array}{l}G\left( x \right) = 2 - 3{x^3} + 6{x^2} + 5x - 2{x^3} - x.\\ = \left( { - 3{x^3} - 2{x^3}} \right) + 6{x^2} + \left( {5x - x} \right) + 2\\ = - 5{x^3} + 6{x^2} + 4x + 2\end{array}\) b) Tính \(M\left( x \right)\) \(\begin{array}{l}M\left( x \right) = F\left( x \right) - G\left( x \right)\\ = \left( { - 5{x^3} + 6{x^2} + 3x - 1} \right) - \left( { - 5{x^3} + 6{x^2} + 4x + 2} \right)\\ = - 5{x^3} + 6{x^2} + 3x - 1 + 5{x^3} - 6{x^2} - 4x - 2\\ = \left( { - 5{x^3} + 5{x^3}} \right) + \left( {6{x^2} - 6{x^2}} \right) + \left( {3x - 4x} \right) + \left( { - 1 - 2} \right)\\ = \,\, - x - 3\end{array}\) Tìm nghiệm của đa thức \(M\left( x \right)\): Ta có: \(M\left( x \right) = - x - 3 = 0 \Leftrightarrow x = - 3\) Vậy \(x = - 3\) là nghiệm của đa thức \(M\left( x \right)\). c) Ta có: \(N\left( x \right) + F\left( x \right) = - G\left( x \right)\) \( \Rightarrow N\left( x \right) = - F\left( x \right) - G\left( x \right)\)\( = - \left[ {F\left( x \right) + G\left( x \right)} \right]\) Trong đó: \(F\left( x \right) = - 5{x^3} + 6{x^2} + 3x - 1\) \(G\left( x \right) = - 5{x^3} + 6{x^2} + 4x + 2\) \( \Rightarrow F\left( x \right) + G\left( x \right)\) \( = \left( { - 5{x^3} + 6{x^2} + 3x - 1} \right)\)\( + \left( { - 5{x^3} + 6{x^2} + 4x + 2} \right)\) \( = - 10{x^3} + 12{x^2} + 7x + 1\) \(\begin{array}{l} \Rightarrow N\left( x \right) = - \left[ {F\left( x \right) + G\left( x \right)} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \left( { - 10{x^3} + 12{x^2} + 7x + 1} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 10{x^3} - 12{x^2} - 7x - 1\end{array}\) Vậy \(N\left( x \right) = 10{x^3} - 12{x^2} - 7x - 1\). LG câu 4 Phương pháp giải: a) Áp dụng định lý Py-ta-go cho \(\Delta ABC\) để tính độ dài cạnh \(AC.\) Sau khi tính được độ dài cạnh \(AC\), dựa vào mối quan hệ giữa ba cạnh của tam giác để so sánh số đo góc của ba góc trong \(\Delta ABC\). Chú ý: Trong một tam giác góc đối diện với cạnh lớn hơn thì lớn hơn. b) Chỉ ra \(\Delta ABC = \Delta AEC\left( {c.g.c} \right)\). c) Trọng tâm của một tam giác là giao điểm của ít nhất hai đường trung tuyến của tam giác đó. Dựa vào tính chất trọng tâm của tam giác để tính cạnh \(CM.\) d) Chứng minh \(K\) là trung điểm của \(BC\). Do đó \(EK\) là đường trung tuyến của \(\Delta BEC\) \( \Rightarrow E,M,K\) là ba điểm thẳng hàng. Lời giải chi tiết:
a) Tính độ dài cạnh \(AC\) và so sánh các góc của tam giác \(ABC\). Tam giác \(ABC\) vuông tại \(A\) nên: \(A{B^2} + A{C^2} = B{C^2}\) (định lý Py-ta-go) \( \Rightarrow A{C^2} = B{C^2} - A{B^2}\)\( = {15^2} - {9^2} = {12^2}\) \( \Rightarrow AC = 12\left( {cm} \right)\). Ta có: \(AB < AC < BC\) \( \Rightarrow \angle C < \angle B < \,\angle A\) (mối quan hệ giữa cạnh và góc trong tam giác). b) Xét \(\Delta ABC\) và \(\Delta AEC\) có: \(AE = AB\) (do \(A\) là trung điểm của \(BE.\)) \(\angle EAC = \angle BAC = {90^0}\left( {gt} \right)\) Cạnh \(AC\) chung. \( \Rightarrow \Delta ABC = \Delta AEC\left( {c.g.c} \right)\) c) Trong tam giác \(BEC\) ta có: \(AE = AB\left( {gt} \right)\) \( \Rightarrow CA\) là đường trung tuyến xuất phát từ đỉnh \(C\). \(BH\) cũng là đường trung tuyến xuất phát từ đỉnh \(B\) của \(\Delta BEC\) Mà \(CA \cap BH = M\) Do đó: \(M\) là trọng tâm của \(\Delta BEC\). \( \Rightarrow CM = \dfrac{2}{3}CA\) \( = \dfrac{2}{3}.12 = 8\left( {cm} \right)\) (tính chất trọng tâm của tam giác). d) Từ \(A\) vẽ đường thẳng song song với \(EC\), đường thẳng này cắt cạnh \(BC\) tại \(K\). Chứng minh rằng ba điểm \(E,M,K\) thẳng hàng. Ta có: \(AK//EC\) (giả thiết) \( \Rightarrow \angle ACE = \angle CAK\) (so le trong) Mà \(\angle ACE = \angle ACK\) (do \(\Delta ABC = \Delta AEC\left( {c.g.c} \right)\)). \( \Rightarrow \angle CAK = \angle ACK\) Do đó: \(\Delta AKC\) cân tại \(K\). \( \Rightarrow CK = AK\) (tính chất tam giác cân). (1) Lại có: \(\begin{array}{l}\angle ACK + \angle B = {90^0}\\\angle CAK + \angle KAB = {90^0}\end{array}\) Mà \(\angle ACK = \angle CAK\left( {cmt} \right)\) Nên \(\angle B = \angle KAB\) Do đó: \(\Delta KAB\) cân tại \(K.\) \( \Rightarrow AK = BK\) (tính chất tam giác cân) (2) Từ (1) và (2) suy ra: \(CK = BK\) \( \Rightarrow K\) là trung điểm của \(BC\) \( \Rightarrow EK\) là đường trung tuyến của \(\Delta EBC\) Do đó: \(E,M,K\) là ba điểm thẳng hàng. LG câu 5 Phương pháp giải: Chứng minh \(f\left( 7 \right) - f\left( 2 \right)\) là một hợp số ta chứng minh nó có thể phân tích được thành tích của hai số tự nhiên nhỏ hơn nó. * Lưu ý: Hợp số là một số tự nhiên chia hết cho các số ngoài 1 và chính nó. Lời giải chi tiết: Theo đề bài, ta có: \(f\left( x \right) = a\,{x^3} + b{x^2} + cx + d\). \(f\left( 5 \right) = 125.a + 25.b + 5.c + d\) \(f\left( 4 \right) = 64a + 16.b + 4.c + d\) \( \Rightarrow f\left( 5 \right) - f\left( 4 \right)\) \( = 61a + 9b + c = 2019\) Lại có: \(f\left( 7 \right) = 343.a + 49.b + 7c + d\) \(f\left( 2 \right) = 8a + 4b + 2c + d\) \(\begin{array}{l} \Rightarrow f\left( 7 \right) - f\left( 2 \right)\\ = 335a + 45b + 5c\\ = 5.\left( {61a + 9b + c} \right) + 30.a=5.2019+60.a\end{array}\) Vì a là số nguyên dương nên 60a chia hết cho 5. Mặt khác, 5.2019 chia hết cho 5. Ta được 5.2019+60a chia hết cho 5(tính chất chia hết của 1 tổng) nên 5.2019+60a là hợp số \( \Rightarrow f\left( 7 \right) - f\left( 2 \right)\) là hợp số (đpcm). Nguồn sưu tầm HocTot.Nam.Name.Vn
|