Đề số 2 - Đề kiểm tra học kì 2 - Toán 7Đáp án và lời giải chi tiết Đề số 2 - Đề kiểm tra học kì 2 - Toán 7
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài I. TRẮC NGHIỆM (2 ĐIỂM) Câu 1: Kết quả thu gọn đơn thức (−34x2y).(−xy3) là: A. 34x3y3 B.−34y4x3 C.34x3y4 D.34x4y3 Câu 2: Giá trị của đa thức P=x2y+2xy+3 tại x=−1,y=2 là A.8 B.1 C.5 D.−1 Câu 3: Tổng của hai đơn thức 4x2y và −8x2y là: A.−4x4y2 B.−32x2y C.−4x2y D.4x2y Câu 4: Cho ΔABC có AB=6cm,BC=8cm,AC=10cm. Số đo góc ∠A;∠B;∠C theo thứ tự là A.∠B<∠C<∠A B.∠C<∠A<∠B C.∠A>∠B>∠C D.∠C<∠B<∠A II. TỰ LUẬN (8 ĐIỂM) Bài 1 (1,5 điểm) Tìm nghiệm của mỗi đa thức sau: a)A(x)=2x−6 b)B(x)=2(x−1)+3(2−x) c)C(x)=8x3−2x Bài 2 (2,5 điểm) Cho 2 đa thức: A(x)=6x2−5x+x3−4x2−7B(x)=−2x2−5x+11+2x2+x3 a) Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến. b) Tính A(2) và B(−1); c) Tính A(x)+B(x) và A(x)−B(x) Bài 3 (3,5 điểm) Cho ΔABC vuông tại A có AB<AC, đường cao AH. Trên cạnh AC lấy điểm E sao cho AH=AE. Qua E kẻ đường thẳng vuông góc với AC, cắt BC tại D. a) Chứng minh ΔAHD=ΔAED b) So sánh DH và DC c) Gọi DE cắt AH tại K. Chứng minh ΔDKC cân tại D. d) Gọi M là trung điểm của KC. Chứng minh ba điểm A,D,M thẳng hàng. Bài 4 (0,5 điểm) Cho đa thức f(x)=ax2+bx+c. Biết f(0)=2017;f(1)=2018;f(−1)=2019. Tính f(2) Đ/án Trắc nghiệm Lời giải chi tiết:
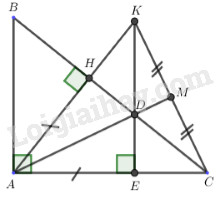
Câu 1: Phương pháp: Muốn nhân hai đơn thức ta nhân hệ số với nhau và nhân phần biến với nhau. Cách giải: Ta có: (−34x2y).(−xy3)=(−34.(−1)).x2.x.y.y3=34.x3.y4 Chọn C. Câu 2: Phương pháp: Thay x=−1,y=2 vào đa thức P để tìm giá trị. Cách giải: Thay x=−1,y=2 vào đa thức P ta có: P(−1;2)=(−1)2.2+2.(−1).2+3=2−4+3=1. Chọn B. Câu 3: Phương pháp: Muốn cộng hai đơn thức đồng dạng ta cộng hệ số với nhau và giữ nguyên phần biến. Ta có: 4x2y+(−8x2y)=[4+(−8)].x2y=−4.x2y Chọn C. Câu 4: Phương pháp: So sánh độ dài các cạnh rồi dựa vào mối quan hệ giữa cạnh và góc trong một tam giác để so sánh các góc với nhau. Trong một tam giác, góc đối diện với cạnh lớn hơn thì góc lớn hơn. Cách giải: ΔABC có AB=6cm,BC=8cm,AC=10cm. Ta có: AB<BC<AC ⇒∠C<∠A<∠B Chọn B.LG bài 1 Phương pháp giải: Để tìm nghiệm của đa thức ta cho đa thức đó bằng 0, sau đó giải phương trình tìm nghiệm. Lời giải chi tiết: a)A(x)=2x−6 Cho A(x)=0 ta có: 2x−6=0⇔2x=6⇔x=3 Vậy x=3 là nghiệm của đa thức A(x). b)B(x)=2(x−1)+3(2−x)=2x−2+6−3x=−x+4 Cho B(x)=0, ta có: −x+4=0⇔x=4 Vậy x=4 là nghiệm của đa thức B(x). c)C(x)=8x3−2x Cho C(x)=0 ta có: 8x3−2x=0⇔2x(4x2−1)=0⇔[x=04x2−1=0⇔[x=0x=±12 Vậy nghiệm của đa thức C(x) là x=0;x=12;x=−12. LG bài 2 Phương pháp giải: a) Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến. b) Thay x=2 vào biểu thức đã thu gọn của A(x) để tìm A(2). Thay x=−1 vào biểu thức đã thu gọn của B(x) để tìm B(−1). c) Thực hiện cộng trừ hai đa thức với nhau theo quy tắc. Lời giải chi tiết: a) Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến. +)A(x)=6x2−5x+x3−4x2−7=x3+(6x2−4x2)−5x−7=x3+2x2−5x−7+)B(x)=−2x2−5x+11+2x2+x3=x3+(2x2−2x2)−5x+11=x3−5x+11 b) Thay x=2 vào A(x) để tìm A(2). Ta có: A(2)=23+2.22−5.2−7=−1 Vậy A(2)=−1. Thay x=−1 vào B(x) để tìm B(−1). Ta có: B(−1)=(−1)3−5(−1)+11=15 Vậy B(−1)=15. c) A(x)+B(x)=(x3+2x2−5x−7)+(x3−5x+11) =(x3+x3)+2x2+(−5x−5x)+11−7 =2x3+2x2−10x+4 Vậy A(x)+B(x)=2x3+2x2−10x+4. A(x)−B(x)=(x3+2x2−5x−7)−(x3−5x+11)=x3+2x2−5x−7−x3+5x−11 =(x3−x3)+2x2+(−5x+5x)+(−7−11) =2x2−18 Vậy A(x)−B(x)=2x2−18 LG bài 3 Phương pháp giải: a) Chứng minh ΔAHD=ΔAED (cạnh huyền-cạnh góc vuông). b) So sánh DH với DE rồi so sánh DE với DC, từ đó kết luận DH<DC. c) Chứng minh DC=DK từ đó suy ra ΔDKC cân tại D. d) Chứng minh D là trực tâm của tam giác cân AKC, sau đó chứng minh AM là đường cao hạ từ đỉnh A của ΔAKC. Suy ra A,D,M thẳng hàng. Lời giải chi tiết:
a) Xét ΔAHDvà ΔAED có: AH=AE(gt)ADchung∠H=∠E=900(gt) ⇒ΔAHD=ΔAED (cạnh huyền-cạnh góc vuông). b) Vì ΔAHD=ΔAED(cmt) do đó: DH=DE (hai cạnh tương ứng) Mà trong ΔDEC có DE<DC (cạnh góc vuông luôn nhỏ hơn cạnh huyền) ⇒DH<DC. c) Xét ΔHAC và ΔEAK có: ∠H=∠E=900(gt) HA=EA(gt) ∠A chung ⇒ΔHAC=ΔEAK(g.c.g) ⇒CH=KE (hai cạnh tương ứng) Mà CH=DC+DHKE=DK+DE Lại có: DH=DE(doΔAHD=ΔAED(cmt)) ⇒DC=DK. Xét ΔDKC có DC=DK(cmt) do đó: ΔDKC cân tại D. d) Xét tam giác AKC ta thấy D là giao điểm của hai đường caoKE và HC ⇒D là trực tâm của ΔAKC Mà AK=AC (do ΔHAC=ΔEAK(cmt)) ⇒ΔAKC cân tại A. Mặt khác M là trung điểm của KC ⇒AM là đường trung tuyến đồng thời là đường cao xuất phát từ đỉnh A. ⇒A,D,M thẳng hàng. LG bài 4 Phương pháp giải: Thay x=0 vào F(x) để tìm c. Thay x=1 và c vừa tìm được vào F(x) để tìm ra biểu thức liên hệ giữa a và b. Thay x=−1 vào F(x), từ đấy tìm ra a và b. Cuối cùng tìm được biểu thức cụ thể của F(x) rồi thay x=2 vào ta tìm được giá trị của F(2). Lời giải chi tiết: Ta có: F(x)=ax2+bx+c Khi đó: F(0)=2017⇒a.02+b.0+c=2017⇒c=2017 F(1)=2018⇒a.12+b.1+c=2018⇒a+b+2017=2018 ⇒a+b=1⇒a=1−b(1) F(−1)=2019⇒a.(−1)2+b(−1)+c=2019⇒a−b+2017=2019⇒a−b=2(2) Thay (1) vào (2) , ta được: (1−b)−b=2⇒1−2b=2⇒2b=−1⇒b=−12 Thay b=−12 vào (1) ta được: a=1−(−12)=32 Khi đó: F(x)=32.x2−12.x+2017 ⇒F(2)=32.22−12.2+2017=6−1+2017=2022 Vậy F(2)=2022. Nguồn sưu tầm HocTot.Nam.Name.Vn
|