Đề số 4 - Đề kiểm tra học kì 2 - Toán 7

Đề bài

Câu 1: Bậc của đa thức $f\left( x \right) =  - 7{x^4} + 4{x^3} + 8{x^2} - 5{x^3}$ $- {x^4} + 5{x^3} + 4{x^4} + 2018$ là:

A. $2018$                   B. $5$

C.$4$                          D.$3$

Câu 2: Kết quả kiểm tra phần thi tâng cầu của môn thể dục được cô giáo ghi lại như sau:

Mỗi học sinh phải tâng được ít nhất 4 quả cầu mới đạt. Số học sinh thi đạt bài kiểm tra là:

A. $3$                                     B.$25$           

C.$23$                                    D.$48$

Câu 3: Cho $\Delta ABC$ biết $BC = 4cm;AB = 5cm;$$AC = 3cm$. Khi đó ta có tam giác $ABC$

A. Nhọn                                  B. Vuông tại A

C. Vuông tại B                       D. Vuông tại C.

Câu 4: Cho $\Delta ABC$ có ba góc nhọn $(AB > AC)$ , đường cao $AH$ , điểm P thuộc đoạn thẳng AH.

Khi đó ta có:

A. $PB \le PC$                                  B.$PB > PC$            

C.$PB < PC$                                     D.$PB \ge PC$

II. TỰ LUẬN (8 điểm)

Câu 5 (2 điểm) Cho các đa thức :$A\left( x \right) = 3{x^3} + 3{x^2} + 2x - 1$ và

$B\left( x \right) = 5{x^4} + 6x - 2{x^2} + 3{x^3}$ $+ 4 - 5{x^4} - 5x$

a) Tìm bậc, hệ số tự do, hệ số cao nhất của $A\left( x \right)$ . Tính $A\left( { - 2} \right).$

b) Thu gọn, sắp xếp đa thức $B\left( x \right)$ theo lũy thừa giảm dần của biến.

c) Tính $A\left( x \right) - B\left( x \right).$

d) Tìm đa thức $C\left( x \right)$ biết $C\left( x \right) - 2.B\left( x \right) = A\left( x \right).$

Câu 6 (2 điểm) Tìm nghiệm của các đa thức sau :

a) $M\left( x \right) = 2x - \dfrac{1}{2}$

b) ${\rm N}\left( x \right) = \left( {x + 5} \right)\left( {4{x^2} - 1} \right)$

c) $P\left( x \right) = 9{x^3} - 25x$

Câu 7 (3,5 điểm) Cho $\Delta ABC$ cân tại A, kẻ AH vuông góc với $BC\left( {H \in BC} \right).$

a) Chứng minh : $HB = HC$ và $AH$ là tia phân giác của $\angle BAC$

b) Lấy $D$ trên tia đối của tia $BC$ sao cho $BD = BH;$ Lấy E trên tia đối của tia BA sao cho $BE = BA.$ Chứng minh rằng : $DE//AH.$

c) So sánh $\angle DAB$ và $\angle BAH$

d) Lấy điểm F sao cho D là trung điểm của EF. Gọi G là trung điểm của EC. Chứng minh rằng : $F,B,G$ thẳng hàng.

Câu 8 (0,5 điểm) Cho đa thức $P\left( x \right) = a\,{x^3} + b{x^2} + cx + d$ có các hệ số $a,b,c,d$ nguyên. Biết $P\left( x \right) \vdots 5$ với mọi số nguyên $x.$ Chứng minh : $a;b;c;d$ chia hết cho 5.

LG câu 1-4

Câu 1 : 

Phương pháp: Thu gọn đa thức rồi xác định bậc của nó. Lưu ý : Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
Cách giải:

Ta có:

$f\left( x \right) =  - 7{x^4} + 4{x^3} + 8{x^2} - 5{x^3}$$- {x^4} + 5{x^3} + 4{x^4} + 2018$

$= \,\left( { - 7{x^4} + 4{x^4} - {x^4}} \right)$$+ \left( { - 5{x^3} + 5{x^3} + 4{x^3}} \right)$$+ 8{x^2} + 2018$

 $= \, - 4{x^4} + 4{x^3} + 8{x^2} + 2018$

Bậc của đa thức là 4.

Chọn C

Câu 2 :

Phương pháp: Tính số học sinh tâng được từ 4 quả trở lên. Ta cộng các tần số của các điểm 4, 5, 6, 7

Cách giải:

Số học sinh tâng được từ 4 quả trở lên là: $25 + 14 + 6 + 3 = 48$

Chọn D

Câu 3 :

Phương pháp: Dựa vào độ dài các cạnh đã cho và lý thuyết về tam giác vuông để đưa ra kết luận.

Cách giải:

Ta thấy cạnh AB lớn nhất $\Rightarrow AB$ là cạnh huyền.

$\Rightarrow \Delta ABC$ vuông tại C.

Chọn D

Câu 4 :

Phương pháp: Có thể vẽ hình để minh họa.

Dựa vào mối liên hệ giữa các cạnh trong tam giác.

Cách giải:

Vì $AB > AC$ nên $PB > PC$

Chọn B

LG câu 5

Phương pháp giải:

a) Thay $x =  - 2$ vào $A\left( x \right)$ để tính $A\left( { - 2} \right)$

b) Thu gọn các số hạng có cùng số mũ và sắp xếp theo số mũ giảm dần.

c) Lưu ý dấu khi phá ngoặc.

d) Rút $C\left( x \right)$ từ biểu thức cho trước và tính.

Lời giải chi tiết:

$a)\,A\left( x \right)$có bậc là 3, hệ số tự do là $- 1$, hệ số cao nhất là 3.

$A\left( { - 2} \right) = 3.{\left( { - 2} \right)^3} + 3.{\left( { - 2} \right)^2} + 2.\left( { - 2} \right) - 1$$= 3.\left( { - 8} \right) + 3.4 - 4 - 1$$=  - 24 + 12 - 5 =  - 17$

$b)\,B\left( x \right) = 5{x^4} + 6x - 2{x^2}$$+ 3{x^3} + 4 - 5{x^4} - 5x$

$= \left( {5{x^4} - 5{x^4}} \right) + 3{x^3}$$- 2{x^2} + \left( {6x - 5x} \right) + 4$

$= 3{x^3} - 2{x^2} + x + 4$

$c)\,A\left( x \right) - B\left( x \right) = 3{x^3} + 3{x^2} + 2x - 1$$- \left( {3{x^3} - 2{x^2} + x + 4} \right)$

$\, = 3{x^3} + 3{x^2} + 2x - 1$$- 3{x^3} + 2{x^2} - x - 4$

$\, = \left( {3{x^3} - 3{x^3}} \right) + \left( {3{x^2} + 2{x^2}} \right)$$+ \left( {2x - x} \right) + \left( { - 1 - 4} \right)$

$= 5{x^2} + x - 5$

$\begin{array}{l}d)\,C\left( x \right) - 2.B\left( x \right) = A\left( x \right)\\ \Rightarrow C\left( x \right) = A\left( x \right) + 2.B\left( x \right)\end{array}$

$= 3{x^3} + 3{x^2} + 2x - 1$$+ 2.\left( {3{x^3} - 2{x^2} + x + 4} \right)$

$= 3{x^3} + 3{x^2} + 2x - 1$$+ \,6{x^3} - 4{x^2} + 2x + 8$

$\, = \,\left( {3{x^3} + 6{x^3}} \right) + \left( {3{x^2} - 4{x^2}} \right)$$+ \left( {2x + 2x} \right) + \left( {8 - 1} \right)$

 $= \,\,9{x^3} - {x^2} + 4x + 7$

LG câu 6

Phương pháp giải:

Cho đa thức bằng 0 và giải tìm x.

Lời giải chi tiết:

a) $M\left( x \right) = 2x - \dfrac{1}{2}$

$\begin{array}{l}M\left( x \right) = 0 \Leftrightarrow 2x - \dfrac{1}{2} = 0\\ \Leftrightarrow 2x = \dfrac{1}{2} \Leftrightarrow x = \dfrac{1}{4}\end{array}$

Vậy nghiệm của đa thức là $x = \dfrac{1}{4}$

b) $N\left( x \right) = \left( {x + 5} \right)\left( {4{x^2} - 1} \right)$

$N\left( x \right) = 0$ $\Leftrightarrow \left( {x + 5} \right)\left( {4{x^2} - 1} \right) = 0$

$\Leftrightarrow x + 5 = 0$ hoặc $4{x^2} - 1 = 0$

$\Leftrightarrow x =  - 5$ hoặc ${x^2} = \dfrac{1}{4}$

$\Leftrightarrow x =  - 5$ hoặc $x = \dfrac{1}{2}$ hoặc $x =  - \dfrac{1}{2}$

Vậy đa thức có 3 nghiệm $x =  - 5$; $x = \dfrac{1}{2}$; $x =  - \dfrac{1}{2}$

c) $P\left( x \right) = 9{x^3} - 25x$

$P\left( x \right) = 0 \Leftrightarrow 9{x^3} - 25x = 0$$\Leftrightarrow x\left( {9{x^2} - 25} \right) = 0$

$\Leftrightarrow x = 0$ hoặc $9{x^2} - 25 = 0$

$\Leftrightarrow x = 0$ hoặc ${x^2} = \dfrac{{25}}{9}$

$\Leftrightarrow x = 0$ hoặc $x = \dfrac{5}{3}$ hoặc $x =  - \dfrac{5}{3}$

Vậy đa thức có 3 nghiệm $x = 0$;$x = \dfrac{5}{3}$; $x =  - \dfrac{5}{3}$

LG câu 7

Phương pháp giải:

a) Chứng minh $\Delta AHB = \Delta AHC$ (cạnh huyền- cạnh góc vuông) từ đó suy ra đpcm

b) Chứng minh DE và AH cùng vuông góc với DH 

c) Dựa vào mối quan hệ giữa cạnh và góc trong tam giác để chứng minh

d) Chứng minh B là trọng tâm và $FG$ là đường trung tuyến trong $\Delta CEF$

Lời giải chi tiết:

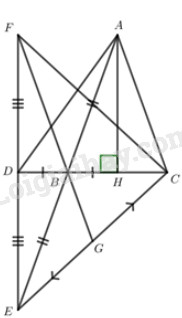
a) Xét $\Delta AHB$ và $\Delta AHC$ có: AH chung ; $\angle AHB = \angle AHC = {90^o}$; $AB = AC$ ($\Delta ABC$ cân tại A)

$\Rightarrow \Delta AHB = \Delta AHC$ (cạnh huyền- cạnh góc vuông) $\Rightarrow HB = HC$ (2 cạnh tương ứng) và $\angle HAB = \angle HAC$ (2 góc tương ứng)

$\Rightarrow$ AH là tia phân giác của $\angle BAC$.

b) Xét $\Delta EDB$ và $\Delta AHB$ có: $BD = BH$ (gt) ;$\angle EBD = \angle ABH$ (đối đỉnh); $BE = BA$ (gt)

$\Rightarrow \Delta EDB = \Delta AHB$ (c.g.c) $\Rightarrow \angle EDB = \angle AHB = {90^o}$ (2 góc tương ứng)

$\Rightarrow$ DE // AH (cùng vuông góc với DH)

c) Ta có DE // AH (cmt) $\Rightarrow \angle BAH = \angle DEA$ (so le trong)

Có $\Delta AHD$ vuông tại H $\Rightarrow AD > AH$ (AD là cạnh huyền)

Mà $AH = ED$ ($\Delta EDB = \Delta AHB$ cmt) $\Rightarrow AD > ED$

Xét $\Delta ADE$ có $AD > ED$$\Rightarrow \angle DEA > \angle DAB$ (mối quan hệ giữa cạnh và góc trong tam giác)

Mà $\angle BAH = \angle DEA$ (cmt) $\Rightarrow \angle DAB < \angle BAH$

d) Có $BD = BH$ (gt) ; $HB = HC$ (cmt) $\Rightarrow BD = BH = CH$

$\Rightarrow CB = BH + CH = 2BH\,\,;\,$ $\,CD = BD + BH + CH = 3BH$

$\Rightarrow \dfrac{{CB}}{{CD}} = \dfrac{{2BH}}{{3BH}} = \dfrac{2}{3}$

 Có D là trung điểm của EF $\Rightarrow CD$ là đường trung tuyến trong $\Delta CEF$ mà $\dfrac{{CB}}{{CD}} = \dfrac{2}{3}$  (cmt)

$\Rightarrow$ B là trọng tâm của $\Delta CEF$

Có G là trung điểm của EC $\Rightarrow FG$ cũng là đường trung tuyến trong $\Delta CEF$

Mà B là trọng tâm của $\Delta CEF$ $\Rightarrow B \in FG \Rightarrow$ F, B, G thẳng hàng.

LG câu 8

Phương pháp giải:

Thay các giá trị $x = 0\,;\,x = 1\,;\,$$x =  - 1\,;\,x = 2$ vào $P\left( x \right)$  kết hợp tính chất chia hết của một tổng để chứng minh.

Lời giải chi tiết:

Ta có $P\left( 0 \right) = d \Rightarrow d \vdots 5$

$P\left( 1 \right) = a + b + c + d$ $\Rightarrow \left( {a + b + c + d} \right) \vdots 5$  (1) $\Rightarrow \left( {a + b + c} \right) \vdots 5$ (do $d \vdots 5$)

$P\left( { - 1} \right) =  - a + b - c + d$ $\Rightarrow \left( { - a + b - c + d} \right) \vdots 5$  (2)

Cộng (1) và (2) ta có: $\left( {2b + 2d} \right) \vdots 5$

Mà $d \vdots 5 \Rightarrow 2d \vdots 5$$\Rightarrow 2b \vdots 5 \Rightarrow b \vdots 5$

$P\left( 2 \right) = 8a + 4b + 2c + d$ $\Rightarrow \left( {8a + 4b + 2c + d} \right) \vdots 5$

$\Rightarrow \left( {8a + 2c} \right) \vdots 5$ (vì $\left( {4b + d} \right) \vdots 5$)

$\Rightarrow \left( {6a + 2a + 2c} \right) \vdots 5$ $\Rightarrow \left[ {6a + 2\left( {a + c} \right)} \right] \vdots 5$

Mà $\left( {a + c} \right) \vdots 5$  (vì $\left( {a + b + c} \right) \vdots 5$ và $b \vdots 5$)

$\Rightarrow 6a \vdots 5 \Rightarrow a \vdots 5 \Rightarrow c \vdots 5$

Vậy a, b, c, d chia hết cho 5.

Nguồn sưu tầm

HocTot.Nam.Name.Vn