Đề số 3 - Đề kiểm tra học kì 1 - Toán 8Tải vềĐáp án và lời giải chi tiết Đề số 3 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 8
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
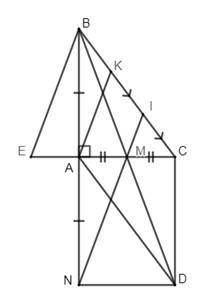
Đề bài Bài 1 (2 điểm)Phân tích các đa thức sau thành nhân tử: a)2x3−50x b)x2−6x+9−4y2 c)x2−7x+10 Bài 2 (1,5 điểm) a.Làm tính chia: (12x6y4+9x5y3−15x2y3):3x2y3 b. Rút gọn biểu thức: (x2−2)(1−x)+(x+3)(x2−3x+9) Bài 3 (2,5 điểm)Cho biểu thức: A=5x+3−23−x−3x2−2x−9x2−9 (với x≠±3) a)Rút gọn biểu thức A. b)Tính giá trị của A khi |x−2|=1 c)Tìm giá trị nguyên của x đểA có giá trị nguyên. Bài 4 (3,5 điểm)Cho ΔABCvuông tại A, gọi M là trung điểm của AC. Gọi D là điểm đối xứng với B qua M. a)Chứng minh tứ giác ABCD là hình bình hành. b)Gọi N là điểm đối xứng với B qua A. Chứng minh tứ giác ACDN là hình chữ nhật. c)Kéo dài MN cắt BC tại I. Vẽ đường thẳng qua A song song với MN cắt BC ởK. Chứng minh: KC=2BK d)Qua B kẻ đường thẳng song song với MN cắt AC kéo dài tại E . Tam giác ABC cần có thêm điều kiện gì để tứ giác EBMN là hình vuông. Bài 5 (0,5 điểm)Cho a thỏa mãn: a2−5a+2=0. Tính giá trị của biểu thức:P=a5−a4−18a3+9a2−5a+2017+(a4−40a2+4):a2 LG bài 1 Lời giải chi tiết: a)2x3−50x=2x(x2−25)=2x(x−5)(x+5) b)x2−6x+9−4y2=(x−3)2−4y2=(x−3+2y)(x−3−2y) c)x2−7x+10=x2−5x−2x+10=(x2−5x)−(2x−10)=x(x−5)−2(x−5)=(x−5)(x−2) LG bài 2 Lời giải chi tiết: a)(12x6y4+9x5y3−15x2y3):3x2y3=(12x6y4:3x2y3)+(9x5y3:3x2y3)−(15x2y3:3x2y3)=4x4y+3x3−5b)(x2−2)(1−x)+(x+3)(x2−3x+9)=x2−x3−2+2x+x3−3x2+9x+3x2−9x+27=x2+2x+25 LG bài 3 Lời giải chi tiết: a)A=5x+3−23−x−3x2−2x−9x2−9(x≠±3)=5x+3+2x−3−3x2−2x−9(x−3)(x+3)=5(x−3)+2(x+3)−3x2+2x+9(x+3)(x−3)=5x−15+2x+6−3x2+2x+9(x+3)(x−3)=−3x2+9x(x+3)(x−3)=−3x(x−3)(x+3)(x−3)=−3xx+3. b)|x−2|=1⇒[x−2=1x−2=−1 ⇒[x=3(ktm)x=1(tm) Với x=1 thay vào A ta có: A=−3.11+3=−34. c) Ta có: A=−3xx+3=−3+9x+3, đểA nguyên ⇔(x+3)∈U(9)={±1;±3;±9}
Vậy với x∈{−2;−4;0;−6;6;−12} thì A nguyên. LG bài 4 Lời giải chi tiết:
a) Ta có: Vì D và B đối xứng với nhau qua M (gt)⇒MD=MB(tính chất hai điểm đối xứng với nhau qua 1 điểm) Xét tứ giác ABCD ta có: {MC=MA(gt)MD=MB(cmt) ⇒ Tứ giác ABCD là hình bình hành (dhnb) b)Vì N đối xứng với B qua A (gt) ⇒NA=AB(tính chất) Lại có ABCD là hình bình hành (cmt) ⇒{DC=ABDC//AB(tính chất) ⇒{DC=ANDC//AN ⇒ANDC là hình bình hành (dhnb) Mặt khác, ∠CAB=900(gt)⇒∠CAN=900 ⇒hình bình hành ANDC là hình chữ nhật (dhnb) (đpcm) c)Xét ΔBNI có: AK//NI (do AK//MN ) NA=AB(gt) ⇒AK là đường trung bình của ΔBNI(định lý) ⇒KI=KB (tính chất) Xét ΔCAK có: MI//AK (do AK//NI) MA=MC (gt) ⇒MI là đường trung bình của ΔACK (dhnb) ⇒IK=CI (tính chất) Mà KC=CI+IK⇒KC=2KI=2KB (do KI=KB) d)Vì BE//MN(gt)⇒BE//IM⇒ Tứ giác BEMI là hình thang (dấu hiệu nhận biết hình thang) Lại có: K là trung điểm của BI (cmt) và AK//MI(cmt)⇒Alà trung điểm của EM (trong hình thang, nếu một đường thẳng đi qua trung điểm của cạnh bên thứ nhất và song song với cạnh đáy thì đi qua trung điểm của cạnh bên thứ hai) Xét tứ giác BENM có hai đường chéo BN và EM cắt nhau tại trung điểm A của mỗi đường. ⇒BENMlà hình bình hành (dhnb) Mà BN⊥EM(gt)⇒ hình bình hành BENM là hình thoi (dhnb) Để hình thoi BENM là hình vuông khi và chỉ khi AB=AM⇔AB=12AC. LG bài 5 Lời giải chi tiết: P=a5−a4−18a3+9a2−5a+2017+(a4−40a2+4):a2=(a5−5a4+2a3)+(4a4−20a3+8a2)+(a2−5a+2)+2015+a4−40a2+4a2=a3(a2−5a+2)+4a2(a2−5a+2)+2015+a4−40a2+4a2=2015+a4−40a2+4a2=a4+1975a2+44. Theo đề bài ta có: a2−5a=−2⇒(a2−5a)2=4⇒a4−10a3+25a2=4 P=a4+1975a2+4a2=(a4−10a3+25a2)+(10a3−50a2+20a)+(4a2−20a+8)+1996a2−4a2=4+10a(a2−5a+2)+4(a2−5a+2)+1996a2−4a2=1996 Vậy P=1996. Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 8 tại HocTot.Nam.Name.Vn HocTot.Nam.Name.Vn
|