Đề số 1 - Đề kiểm tra học kì 1 - Toán 8

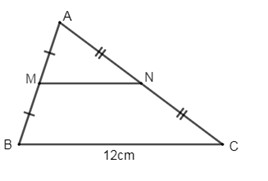
Đề bài

Bài 3 (2,0 điểm)Cho biểu thức:  \(A = \dfrac{{2{x^2}}}{{{x^2} - 1}} + \dfrac{x}{{x + 1}} - \dfrac{x}{{x - 1}}\)

a) Với giá trị nào của \(x\) thì giá trị của biểu thức\(A\)được xác định?

b)Rút gọn biểu thức \(A\).

c)Tìm các giá trị nguyên của\(x\)để biểu thức\(A\)có giá trị nguyên.

Bài 4 (3,5 điểm) Cho \(\Delta ABC\)vuông tại\(A\), đường cao \(AM\). Gọi \(D,\,E\) lần lượt là chân các đường vuông góc kẻ từ \(M\) đến các cạnh\(AB,\,AC\).

a)Tứ giác\(A{\rm{D}}ME\) là hình gì? Vì sao?

b)Chứng minh: \(AM.BC = AB.AC\)

c)Gọi\(I\)là trung điểm của\(MC\). Chứng minh rằng \(\Delta DEI\) vuông.

d) \(\Delta ABC\) phải có thêm điều kiện gì để \(DE = 2{\rm{E}}I\).

Bài 5 (0,5 điểm) Cho \(x,y\)thỏa mãn đẳng thức \(2{x^2} + 2{y^2} + 3xy - x + y + 1 = 0\). Tính giá trị của biểu thức \(P = {\left( {x + 2y} \right)^5} + {\left( {y + 1} \right)^4} + {\left( {x - 2} \right)^3}\).

LG bài 1

Lời giải chi tiết:

1.      Thực hiện phép tính:

a)\(2x\left( {{x^2} - 3y} \right) = 2x.{x^2} - 2x.3y = 2{x^3} - 6xy\)

b)\( - 18{x^3}{y^4}:3x{y^4} =  - \dfrac{{18{x^3}{y^4}}}{{3x{y^4}}} =  - 6{x^2}.\)

2.

Cho \(\Delta ABC\)có cạnh\(BC = 12cm\). Gọi\(M\)và\(N\)lần lượt là trung điểm của các cạnh\(AB,\,AC\) . Tính\(MN\) .

Vì\(M,\,N\)là trung điểm của\(AB,\,AC\) (gt)

\( \Rightarrow MN\)là đường trung bình của\(\Delta ABC\) (dấu hiệu nhận biết đường

trung bình của tam giác)

\( \Rightarrow MN = \dfrac{{BC}}{2} = 12:2 = 6cm\) (tính chất đường trung bình của tam giác)

LG bài 2

Lời giải chi tiết:

1.      Tìm x biết:

\(\begin{array}{l}a)\,\,{\left( {x + 2} \right)^2} - \left( {x - 2} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x + 2 - x + 2} \right) = 0\\ \Leftrightarrow 4\left( {x + 2} \right) = 0\\ \Leftrightarrow x + 2 = 0\\ \Leftrightarrow x =  - 2\end{array}\)

\(\begin{array}{l}b)\,\,\,\left( {{x^2} - 2x + 1} \right):\left( {x - 1} \right) + 5x = 8\\ \Leftrightarrow {\left( {x - 1} \right)^2}:\left( {x - 1} \right) + 5x = 8\\ \Leftrightarrow x - 1 + 5x = 8\\ \Leftrightarrow 6x = 9\\ \Leftrightarrow x = \dfrac{3}{2}\end{array}\)

 2.      Phân tích đa thức sau thành nhân tử:

\(a)\,\,2{x^2} - 14x\,{\rm{ = }}\,{\rm{2}}x\left( {x - 7} \right)\)

\(\begin{array}{l}b)\,\,{x^2} - {y^2} + 5x + 5y = \left( {{x^2} - {y^2}} \right) + 5\left( {x + y} \right)\\ = \left( {x + y} \right)\left( {x - y} \right) + 5\left( {x + y} \right)\\ = \left( {x + y} \right)\left( {x - y + 5} \right).\end{array}\)

LG bài 3

Lời giải chi tiết:

Cho biểu thức\(A = \dfrac{{2{x^2}}}{{{x^2} - 1}} + \dfrac{x}{{x + 1}} - \dfrac{x}{{x - 1}}\)

a) Để A xác định\( \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 1 \ne 0\\x + 1 \ne 0\\x - 1 \ne 0\end{array} \right. \Leftrightarrow x \ne  \pm 1\)

b) Điều kiện: \(x \ne  \pm 1.\)

\(\begin{array}{l}A = \dfrac{{2{x^2}}}{{{x^2} - 1}} + \dfrac{x}{{x + 1}} - \dfrac{x}{{x - 1}} \\\;\;\;= \dfrac{{2{x^2} + x\left( {x - 1} \right) - x\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\\;\;\; = \dfrac{{2{x^2} + {x^2} - x - {x^2} - x}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} \\\;\;\;= \dfrac{{2{x^2} - 2x}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\\;\;\; = \dfrac{{2x\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \dfrac{{2x}}{{x + 1}}.\end{array}\)

c) Điều kiện: \(x \ne  \pm 1.\)

Ta có: \(A = \dfrac{{2x}}{{x + 1}} = 2 - \dfrac{2}{{x + 1}}\)

Để\(A\)đạt giá trị nguyên thì \(2 \vdots \left( {x + 1} \right) \Rightarrow \left( {x + 1} \right) \in \) Ư(2) \( = \left\{ { \pm 1; \pm 2} \right\}\)

Vậy với \(x \in \left\{ {0; - 2; - 3} \right\}\) thì \(A\) nguyên.

LG bài 4

Lời giải chi tiết:

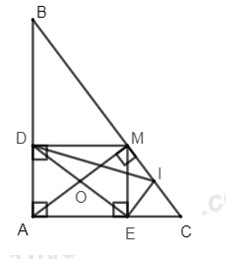
a) Vì \(\left\{ \begin{array}{l}M{\rm{D}} \bot AB\\ME \bot AC\end{array} \right.\left( {gt} \right) \Rightarrow \angle M{\rm{D}}A = \angle ME{\rm{A}} = {90^0}\)

Xét tứ giác \(A{\rm{D}}ME\)có: \(\left\{ \begin{array}{l}\angle MDA = \angle ME{\rm{A}} = {90^0}\left( {cmt} \right)\\\angle DAE = {90^0}\left( {gt} \right)\end{array} \right.\)

\( \Rightarrow \) Tứ giác \(A{\rm{D}}ME\) là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)

b)Xét \(\Delta AMC\) và \(\Delta BAC\) có:

\(\left\{ \begin{array}{l}\angle AMC = \angle BAC = {90^0}\left( {gt} \right)\\\angle C\,\,chung\end{array} \right. \Rightarrow \Delta AMC \sim \Delta BAC\left( {g - g} \right)\)

\( \Rightarrow \dfrac{{AM}}{{AB}} = \dfrac{{AC}}{{BC}} \Rightarrow AM.BC = AB.AC\) (tính chất hai tam giác đồngdạng)

c)Gọi \(O\) là giao điểm của \(DE\) và \(AM\). Ta có \(DME{\rm{A}}\) là hình chữ nhật (cmt)

\( \Rightarrow OM = OE\) (tính chất hình chữ nhật)

\( \Rightarrow \Delta OM{\rm{E}}\)cân tại\(O\) (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow \angle OME = \angle OEM\) (tính chất tam giác cân)

Xét \(\Delta MEC\) vuông tại \(E\) và có \(I\) là trung điểm của \(MC\) (gt)

\( \Rightarrow EI = \dfrac{{MC}}{2}\left( 1 \right)\) (tính chất trong tam giác vuông, đường trung tuyến  ứng với cạnh huyền bằng nửa cạnh ấy)

Mà\(I\)là trung điểm của\(MC\) (gt) \( \Rightarrow MI = IC\left( 2 \right)\) (tính chất trung điểm)

Từ (1) và (2) suy ra\(EI = MI \Rightarrow \Delta MIE\)cân tại\(I\) (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow \angle IME = \angle IEM\) (tính chất tam giác cân)

Mặtkhác, \(\angle AME + \angle EMC = {90^0} \Rightarrow \angle DEM + \angle MEI = {90^0}\)

\( \Rightarrow \Delta DEI\) vuông tại \(E\) (dấu hiệu nhận biết tam giác cân)

d)Vì\(EI = \dfrac{{MC}}{2}\left( {cmt} \right) \Rightarrow MC = 2{\rm{E}}I\). Mà\(DE = 2{\rm{E}}I \Rightarrow DE = MC\)

Suyra \(D,\,E\) là trung điểm của \(AB\)và\(AC\). Thật vậy, ta có:

\(D,\,E\)là trung điểm của \(AB\) và \(AC\) \( \Rightarrow DE\)là đường trung bình của\(\Delta ABC\) (dấu hiệu nhận biết đường trung bình của tam giác)

\( \Rightarrow DE//BC\) (tính chất đường trung bình của tam giác) (3)

Mà DMEA là hình chữ nhật (cmt) \( \Rightarrow DM//A{\rm{E}}\) (tính chất hình chữ nhật)

Hay \(DM//EC\left( 4 \right)\) .

Từ (3) và (4) suy ra tứ giác\(DMCE\)là hình bình hành (dấu hiệu nhận biết hình bình hành)

\( \Rightarrow DE = MC\) (tính chất hình bình hành)

Mà\(MC = 2{\rm{E}}I\left( {cmt} \right) \Rightarrow DE = 2{\rm{E}}I\).

Vậy để\(DE = 2{\rm{E}}I\)thì\(D,\,E\)là trung điểm của\(AB\)và\(AC\).

LG bài 5

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}\;\;\;\;\;2{x^2} + 2{y^2} + 3xy - x + y + 1 = 0\\ \Leftrightarrow 4{x^2} + 4{y^2} + 6xy - 2x + 2y + 2 = 0\\ \Leftrightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} + 2y + 1} \right) + 3\left( {{x^2} + {y^2} + 2xy} \right) = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} + 3{\left( {x + y} \right)^2} = 0\\ \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 0\\y + 1 = 0\\x + y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 1\\x =  - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 1\end{array} \right.\end{array}\)

Thay\(\left\{ \begin{array}{l}x = 1\\y =  - 1\end{array} \right.\)vào\(P = {\left( {x + 2y} \right)^5} + {\left( {y + 1} \right)^4} + {\left( {x - 2} \right)^3}\)ta được:

\(P = {\left( {1 - 2} \right)^5} + {\left( { - 1 + 1} \right)^4} + {\left( {1 - 2} \right)^3} =  - 2\).

Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 8 tại HocTot.Nam.Name.Vn

 HocTot.Nam.Name.Vn