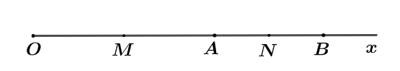Đề thi học kì 2 Toán 6 - Đề số 3 - Kết nối tri thứcTải về Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Tổng hợp đề thi học kì 1 lớp 6 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1: Cho đoạn thẳng AB = 6 cm. Điểm K nằm giữa AB, biết KA = 4 cm thì đoạn thẳng KB bằng: A. 10 cm B. 6 cm C. 4 cm D. 2 cm Câu 2: Bạn Nam có một cái hộp đựng 1 chiếc bút xanh, 2 chiếc bút đỏ và 1 chiếc bút đen. Nam lấy ngẫu nhiên cùng lúc 3 chiếc bút trong hộp. Kết quả nào sau đây chắc chắn sẽ xảy ra? A. Luôn lấy được một chiếc bút đỏ. B. Luôn lấy được một chiếc bút xanh. C. Luôn lấy được một chiếc bút đen. D. Luôn lấy được 3 chiếc, ba màu khác nhau. Câu 3: Thực hiện phép tính rồi làm tròn kết quả đến hàng phần trăm: \(96,3\,.\,3,007\) A. \(289,5\) B. \(289,57\) C. \(289,58\) D. \(289,6\) Câu 4: Cho \(\dfrac{3}{x} = \dfrac{y}{{12}} = \dfrac{1}{4}\) thì giá trị của \(x\) và \(y\) là: A. \(x = 4;y = 9\) B. \(x = - 4;y = - 9\) C. \(x = 12;y = 3\) D. \(x = - 12;y = - 3\) Phần II. Tự luận (8 điểm): Bài 1: (2 điểm) Thực hiện phép tính (Tính hợp lý nếu có thể) a) \(2\dfrac{1}{9} - \dfrac{1}{3}:\dfrac{3}{7}\) b) \(\dfrac{7}{{19}}.\dfrac{8}{{11}} + \dfrac{3}{{11}}.\dfrac{7}{{19}} + \dfrac{{ - 12}}{{19}}\) c) \(20\dfrac{8}{{23}} - \left( {5\dfrac{7}{{32}} + 14\dfrac{8}{{23}}} \right)\) d) \(75\% {\rm{\;}} - 1\dfrac{1}{2} + 0,5:\dfrac{5}{{12}} - {\left( { - \dfrac{1}{2}} \right)^2}\) Bài 2: (1,5 điểm) Tìm x biết: \(a)\,\,x - \dfrac{1}{3} = \dfrac{5}{{14}} \cdot \dfrac{{ - 7}}{6}\,\,\) \(b)\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = 0,2\) \(c)\,\,\dfrac{1}{{12}}.{x^2} = 1\dfrac{1}{3}\) Bài 3 (1,5 điểm) Một bác nông dân vừa thu hoạch 30,8 kg cà chua và 12 kg đậu đũa. a) Bác đem số cà chua đó đi bán hết, giá mỗi kg cà chua là 15 000 đồng. Hỏi bác nông dân nhận được bao nhiêu tiền? b) Số đậu đũa bác vừa thu hoạch chỉ bằng \(\dfrac{2}{5}\) số đậu đũa có trong vườn. Nếu bác thu hoạch hết tất cả thì thu được bao nhiêu kg đậu đũa? Bài 4: (2,5 điểm) Trên tia \(Ox\) lấy hai điểm \(A,{\kern 1pt} {\kern 1pt} B\) sao cho \(OA = 5cm,{\kern 1pt} {\kern 1pt} OB = 8cm\). a) Trong ba điểm \(O,{\kern 1pt} {\kern 1pt} A,{\kern 1pt} {\kern 1pt} B\) điểm nào nằm giữa hai điểm còn lại? b) Tính độ dài đoạn thẳng \(AB\). c) Điểm \(A\) có phải là trung điểm của đoạn thẳng \(OB\) không? Vì sao? d) Gọi \(M\) là trung điểm của \(OA\), \(N\) là trung điểm của \(AB\). Tính độ dài đoạn thẳng \(MN\)? Bài 5: (0,5 điểm) Tính nhanh : \(S = 1 + \dfrac{1}{{1 + 2}} + \dfrac{1}{{1 + 2 + 3}} + \dfrac{1}{{1 + 2 + 3 + 4}} + ... + \dfrac{1}{{1 + 2 + 3 + 4 + ... + 8}}\). Lời giải Phần I: Trắc nghiệm
Câu 1 Phương pháp: Dựa vào tính chất điểm nằm giữa hai điểm: Khi M nằm giữa A và B thì \(AM + MB = AB\) Cách giải: Vì K nằm giữa A và B nên ta có: \(AK + KB = AB\) Hay \(4 + KB = 6\) Suy ra: \(KB = 6 - 4 = 2\left( {cm} \right)\) Chọn D. Câu 2 Phương pháp: Liệt kê các trường hợp có thể xảy ra Cách giải: Lấy ngẫu nhiên \(3\) chiếc bút có thể đưa ra các kết quả sau: + Trường hợp 1: \(1\) xanh, \(1\) đỏ, \(1\) đen. + Trường hợp 2: \(1\) xanh, \(2\) đỏ. + Trường hợp 3: \(2\) đỏ, \(1\) đen. Ta thấy trong cả 3 trường hợp trên ta luôn lấy được ít nhất \(1\) chiếc bút màu đỏ. Chọn A. Câu 3 Phương pháp: Thực hiện phép tính nhân hai số thập phân. Cách giải: Ta có: \(96,3\,.\,3,007 = 289,5741 \approx 289,57\) Chọn B. Câu 4 Phương pháp: Quy đồng mẫu số để tìm y, quy đồng tử số để tìm x. Cách giải: Ta có: \(\dfrac{3}{x} = \dfrac{y}{{12}} = \dfrac{3}{{12}}\) Vậy: \(x = 12;y = 3\) Chọn C. Phần II: Tự luận Bài 1 Phương pháp Áp dụng các quy tắc : - Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc: Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ. - Thứ tự thực hiện các phép tính đối với biểu thức có dấu ngoặc: \(({\kern 1pt} {\kern 1pt} ){\kern 1pt} {\kern 1pt} \to [{\kern 1pt} {\kern 1pt} ]{\kern 1pt} {\kern 1pt} \to \{ {\kern 1pt} {\kern 1pt} \} \) Cách giải: a) \(2\dfrac{1}{9} - \dfrac{1}{3}:\dfrac{3}{7}\) \(\begin{array}{l} = \dfrac{{19}}{9} - \dfrac{1}{3}.\dfrac{7}{3}\\ = \dfrac{{19}}{9} - \dfrac{7}{9}\\ = \dfrac{{12}}{9} = \dfrac{4}{3}\end{array}\) b) \(\dfrac{7}{{19}}.\dfrac{8}{{11}} + \dfrac{3}{{11}}.\dfrac{7}{{19}} + \dfrac{{ - 12}}{{19}}\) \(\begin{array}{l} = \dfrac{7}{{19}}.\left( {\dfrac{8}{{11}} + \dfrac{3}{{11}}} \right) + \dfrac{{ - 12}}{{19}}\\ = \dfrac{7}{{19}}.\dfrac{{11}}{{11}} + \dfrac{{ - 12}}{{19}}\\ = \dfrac{7}{{19}} + \dfrac{{ - 12}}{{19}} = \dfrac{{ - 5}}{{19}}\end{array}\) c) \(20\dfrac{8}{{23}} - \left( {5\dfrac{7}{{32}} + 14\dfrac{8}{{23}}} \right)\) \(\begin{array}{l} = 20 + \dfrac{8}{{23}} - \left( {5 + \dfrac{7}{{32}} + 14 + \dfrac{8}{{23}}} \right)\\ = 20 + \dfrac{8}{{23}} - 5 - \dfrac{7}{{32}} - 14 - \dfrac{8}{{23}}\\ = \left( {20 - 5 - 14} \right) + \left( {\dfrac{8}{{23}} - \dfrac{8}{{23}}} \right) - \dfrac{7}{{32}}\\ = 1 + 0 - \dfrac{7}{{32}}\\ = 1 - \dfrac{7}{{32}}\\ = \dfrac{{32}}{{32}} - \dfrac{7}{{32}}\\ = \dfrac{{25}}{{32}}\end{array}\) d) \(75\% - 1\dfrac{1}{2} + 0,5:\dfrac{5}{{12}} - {\left( { - \dfrac{1}{2}} \right)^2}\) \(\begin{array}{l} = \dfrac{3}{4} - \dfrac{3}{2} + \dfrac{1}{2}.\dfrac{{12}}{5} - \dfrac{1}{4}\\ = \dfrac{3}{4} - \dfrac{3}{2} + \dfrac{6}{5} - \dfrac{1}{4}\\ = \dfrac{3}{4} - \dfrac{1}{4} - \dfrac{3}{2} + \dfrac{6}{5}\\ = \dfrac{2}{4} - \dfrac{3}{2} + \dfrac{6}{5}\\ = \dfrac{1}{2} - \dfrac{3}{2} + \dfrac{6}{5}\\ = \dfrac{{ - 2}}{2} + \dfrac{6}{5}\\ = - 1 + \dfrac{6}{5}\\ = \dfrac{{ - 5}}{5} + \dfrac{6}{5} = \dfrac{1}{5}\end{array}\) Bài 2: Phương pháp: Áp dụng quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”. Cách giải: \(\begin{array}{l}a)\,\,x - \dfrac{1}{3} = \dfrac{5}{{14}} \cdot \dfrac{{ - 7}}{6}\,\\\,\,\,\,\,\,x - \dfrac{1}{3} = \dfrac{{ - 5}}{{12}}\,\,\,\\\,\,\,\,\,\,x = \dfrac{{ - 5}}{{12}}\, + \dfrac{1}{3}\,\\\,\,\,\,\,\,x = \dfrac{{ - 1}}{{12}}\,\end{array}\) Vậy \(x = \dfrac{{ - 1}}{{12}}\) \(\begin{array}{l}\,b)\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = 0,2\,\\\,\,\,\,\,\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = \dfrac{1}{5}\,\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4} \cdot x = \dfrac{1}{5} - \dfrac{3}{4}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4} \cdot x = \dfrac{{ - 11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \,\,\dfrac{{ - 11}}{{20}}:\dfrac{1}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \,\dfrac{{ - 11}}{5}\end{array}\) Vậy \(x = \dfrac{{ - 11}}{5}\) \(\begin{array}{l}c)\,\,\dfrac{1}{{12}}.{x^2} = 1\dfrac{1}{3}\\\,\dfrac{1}{{12}}.{x^2} = \dfrac{4}{3}\\{x^2} = \dfrac{4}{3}:\dfrac{1}{{12}}\\{x^2} = 16\\ \Rightarrow \,\left[ \begin{array}{l}x = 4\\x = - 4\end{array} \right.\end{array}\) Vậy \(x \in \left\{ {4; - 4} \right\}\) Bài 3 Phương pháp: Phương pháp: Lấy giá tiền 1 kg cà chua nhân với khối lượng cà chua. Cách giải: Số tiền bác nông dân nhận được là: \(15000.30,8 = 462000\)(đồng) b) (VD): Phương pháp: Lấy khối lượng đậu đũa vừa thu hoạch chia cho \(\dfrac{2}{5}\). Cách giải: Nếu thu hoạch hết thì thu được số ki-lô-gam đậu đũa là: \(12:\dfrac{2}{5} = 30\)(kg) Bài 4 Phương pháp Áp dụng tính chất trung điểm của một đoạn thẳng và công thức cộng đoạn thẳng. Cách giải:
a) Ta có: \(A\) và \(B\) cùng thuộc tia \(Ox\) và \(OA < OB{\kern 1pt} {\kern 1pt} \left( {5cm < 8cm} \right)\) nên \(A\) nằm giữa \(O\) và \(B\). b) Vì \(A\) nằm giữa \(O\) và \(B\) nên ta có: \(OB = OA + AB\) \(AB = OB - OA\) \(AB = 8cm - 5cm\) \(AB = 3cm\) c) Vì \(AB = 3cm\) và \(OA = 5cm\) suy ra \(AB \ne OA\) nên \(A\) không phải là trung điểm của \(OB\). Vì \(M\) là trung điểm của \(AO\) nên \(MA = \dfrac{{OA}}{2} = \dfrac{5}{2} = 2,5{\kern 1pt} {\kern 1pt} \left( {cm} \right)\) Vì \(N\) là trung điểm của \(AB\) nên \(NA = \dfrac{{AB}}{2} = \dfrac{3}{2} = 1,5{\kern 1pt} {\kern 1pt} \left( {cm} \right)\) Vì \(A\) nằm giữa \(O\) và \(B\) nên \(AO\) và \(AB\) là hai tia đối nhau. Mặt khác, \(M\) là trung điểm của \(OA\) và \(N\) là trung điểm của \(AB\) nên \(A\) nằm giữa \(M\) và \(N\). Do đó, ta có: \(MN = MA + AN = 2,5cm + 1,5cm = 4cm\) Vậy \(MN = 4cm\). Bài 5 Phương pháp Đưa tổng đã cho về dạng: \(S = 1 + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{36}}.\) Tính \(\dfrac{1}{2}S\) sau đó suy ra giá trị của biểu thức \(S.\) Cách giải: \(\begin{array}{*{20}{l}}{S = 1 + \dfrac{1}{{1 + 2}} + \dfrac{1}{{1 + 2 + 3}} + \dfrac{1}{{1 + 2 + 3 + 4}} + ... + \dfrac{1}{{1 + 2 + 3 + 4 + ... + 8}}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 1 + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{36}}}\\{ \Rightarrow \dfrac{1}{2}.S = \dfrac{1}{2}\left( {1 + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{36}}} \right)}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \dfrac{1}{2} + \dfrac{1}{6} + \dfrac{1}{{12}} + \dfrac{1}{{20}} + ... + \dfrac{1}{{72}}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + ... + \dfrac{1}{{8.9}}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left( {1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + \dfrac{1}{4} - \dfrac{1}{5} + ... + \dfrac{1}{8} - \dfrac{1}{9}} \right)}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 1 - \dfrac{1}{9} = \dfrac{8}{9}}\\{ \Rightarrow \dfrac{1}{2}S = \dfrac{8}{9}}\\{ \Rightarrow S = \dfrac{8}{9}:\dfrac{1}{2} = \dfrac{{16}}{9}.}\end{array}\)
|