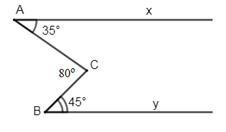
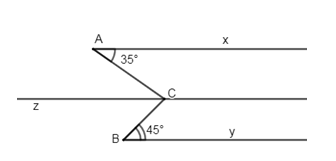
Đề kiểm tra giữa kì I Toán 7 - Đề số 7 có lời giải chi tiếtĐề kiểm tra giữa kì I Toán 7 - Đề số 7 có lời giải chi tiết Đề bài I. TRẮC NGHIỆM (2,5 điểm) Khoanh tròn đáp án trước câu trả lời đúng: Câu 1: Kết quả của phép tính \({\left( {\frac{1}{3}} \right)^9}:{\left( {\frac{1}{9}} \right)^3}\) A. \({\left( {\frac{1}{3}} \right)^3}\) B. \({\left( { - \frac{1}{3}} \right)^3}\) C. \(\frac{1}{3}\) D. \( - \frac{1}{3}\) Câu 2: Nếu \(\sqrt {x + 3} = 4\) thì \(x\) bằng: A. \(16\) B. \( \pm 13\) C. \(13\) D. \( \pm 169\) Câu 3: Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\,\,\left( {a,b,c,d \ne 0} \right)\) ta có thể suy ra A. \(\frac{a}{c} = \frac{d}{b}\,\) B. \(\frac{a}{d} = \frac{b}{c}\,\) C. \(\frac{b}{a} = \frac{d}{c}\,\) D. \(\frac{a}{b} = \frac{d}{c}\,\) Câu 4: Cho đường thẳng \(c\)cắt hai đường thẳng \(a\) và \(b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì: A. \(a//b\) B. \(a\) cắt \(b\) C. \(a \bot b\) D. \(a\) trùng với \(b\) Câu 5: Cho \(\Delta ABC\) có \(\angle A = 40^\circ ;\,\,\angle C = 80^\circ \). Góc ngoài của tam giác tại đỉnh \(B\) có số đo là: A. \(140^\circ \) B. \(100^\circ \) C. \(60^\circ \) D. \(120^\circ \) II. TỰ LUẬN (7,5 điểm) Câu 1 (2 điểm)Thực hiện phép tính: \(a)\,\,\frac{4}{{13}}.15\frac{3}{{41}} - \frac{4}{{13}}.2\frac{3}{{41}}\) \(b)\,\,\sqrt {25} .\left( {0,4 - 1\frac{1}{2}} \right):\left[ {{{\left( { - 2} \right)}^3}.\frac{{11}}{8}} \right]\) Câu 2 (2 điểm): a) Tìm \(x\) biết: \(\frac{3}{4} + \frac{1}{4}:x = 2\). b) Tìm \(x,y\) biết: \(3x = 2y\)và \(x - 2y = 8\) Câu 3 (2 điểm) Ba lớp 7A, 7B, 7C có tất cả 153 học sinh. Số học sinh lớp 7B bằng \(\frac{8}{9}\) số học sinh lớp 7A, số học sinh lớp 7C bằng \(\frac{{17}}{{16}}\) số học sinh lớp 7B. Tính số học sinh của lớp 7A. Câu 4 (1 điểm): Cho hình vẽ sau: Biết \(\widehat {xAC} = {35^0},\,\widehat {CBy} = {45^0}\) và \(\widehat {ACB} = {80^0}.\) Chứng minh rằng \(Ax\,//\,By\) . Bài 5 (0,5 điểm) Cho \(a + b + c = {a^2} + {b^2} + {c^2} = 1\) và \(\frac{x}{a} = \frac{y}{b} = \frac{z}{c}\) (với \(a \ne 0;\,\,b \ne 0;\,\,c \ne 0\)). Chứng minh rằng : \({\left( {x + y + z} \right)^2} = {x^2} + {y^2} + {z^2}\).
Lời giải chi tiết I. TRẮC NGHIỆM
Câu 1: Phương pháp: Sử dụng công thức \({a^m}:{a^n} = {a^{m - n}}\) Cách giải: \(\begin{array}{l}{\left( {\frac{1}{3}} \right)^9}:{\left( {\frac{1}{9}} \right)^3} = {\left( {\frac{1}{3}} \right)^9}:{\left( {\frac{1}{3}} \right)^6}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\left( {\frac{1}{3}} \right)^{9 - 6}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\left( {\frac{1}{3}} \right)^3}\end{array}\) Chọn A. Câu 2: Phương pháp: Sử dụng công thức \(\sqrt A = B\left( {B > 0} \right)\) thì \(A = {B^2}\) Cách giải: \(\begin{array}{l}\sqrt {x + 3} = 4\\ \Leftrightarrow x + 3 = {4^2}\\ \Leftrightarrow x + 3 = 16\\ \Leftrightarrow x = 16 - 3\\ \Leftrightarrow x = 13\end{array}\) Vậy \(x = 13.\) Chọn C. Câu 3: Phương pháp: Sử dụng tính chất tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Cách giải: Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\,\,\left( {a,b,c,d \ne 0} \right)\) ta có thể suy ra \(\frac{b}{a} = \frac{d}{c}\). Chọn C. Câu 4: Phương pháp: Sử dụng dấu hiệu nhận biết hai đường thẳng song song. Cách giải: Nếu đường thẳng \(c\)cắt hai đường thẳng \(a\) và \(b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì \(a//b\). Chọn A. Câu 5: Phương pháp: Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó. Cách giải: Số đo góc ngoài tại đỉnh \(B\) của tam giác \(ABC\) là \({40^0} + {80^0} = {120^0}\). Chọn D. II: TỰ LUẬN Câu 1: Phương pháp: a) Sử dụng tính chất phân phối của phép nhân và cộng \(ab + ac = a\left( {b + c} \right)\). b) Đưa về phân số và tính toán. Cách giải:
Câu 2 : Phương pháp: a) Sử dụng quy tắc chuyển vế đổi dấu. b) Sử dụng tính chất dãy tỉ số bằng nhau \(\frac{a}{x} = \frac{b}{y} = \frac{{ma \pm nb}}{{mx \pm ny}}\) Cách giải:
Câu 3: Phương pháp: + Gọi số học sinh lớp 7A, 7B, 7C lần lượt là \(x;y;z\,\left( {x;y;z > 0} \right)\) + Sử dụng dữ kiện đề bài suy ra mối quan hệ của \(x;y;z\) từ đó lập được tỉ lệ thức + Áp dụng tính chất dãy tỉ số bằng nhau để giải bài toán Cách giải: Gọi số học sinh lớp 7A, 7B, 7C lần lượt là \(x;y;z\,\left( {x;y;z > 0} \right)\) Theo bài ra ta có \(x + y + z = 153\); \(y = \frac{8}{9}x;\,z = \frac{{17}}{{16}}y\) Suy ra \(9y = 8x \Rightarrow \frac{x}{9} = \frac{y}{8} \Rightarrow \frac{x}{{18}} = \frac{y}{{16}}\) ; \(16z = 17y \Rightarrow \frac{z}{{17}} = \frac{y}{{16}}\) Nên \(\frac{x}{{18}} = \frac{y}{{16}} = \frac{z}{{17}}\) Áp dụng tính chất dãy tỉ số bằng nhau ta có \(\frac{x}{{18}} = \frac{y}{{16}} = \frac{z}{{17}}\)\( = \frac{{x + y + z}}{{18 + 16 + 17}} = \frac{{153}}{{51}} = 3\) Do đó: \(x = 18.3 = 54\); \(y = 16.3 = 48\); \(z = 17.3 = 51\) Số học sinh lớp \(7A\) là \(54\) học sinh. Câu 4: Phương pháp: + Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau. + Dấu hiệu nhận biết hai đường thẳng song song. Cách giải: Kẻ \(Cz//{\rm{Ax}} \Rightarrow \widehat {xAC} = \widehat {ACz} = {35^0}\) (so le trong) Ta có: \(\widehat {ACz} + \widehat {zCB} = \widehat {ACB} \Rightarrow \widehat {zCB} = \widehat {ACB} - \widehat {ACz} = {80^0} - {35^0} = {45^0}\) \( \Rightarrow \widehat {zCB} = \widehat {CBy}\left( { = {{45}^0}} \right)\) Mà hai góc ở vị trí so le trong nên suy ra \(Cz//\,By\) (dấu hiệu nhận biết hai đường thẳng song song) Ta có: \(\left\{ \begin{array}{l}Cz//\,Ax\left( {gt} \right)\\C{\rm{z}}//\,By\left( {cmt} \right)\end{array} \right. \Rightarrow Ax//\,By\) . Câu 5: Phương pháp: Sử dụng tính chất dãy tỉ số bằng nhau \(\frac{x}{a} = \frac{y}{b} = \frac{z}{c} = \frac{{x + y + z}}{{a + b + c}}\) Cách giải: Theo giả thiết ta có : \(\frac{x}{a} = \frac{y}{b} = \frac{z}{c}\). Áp dụng dãy tỉ số bằng nhau ta có: \(\frac{x}{a} = \frac{y}{b} = \frac{z}{c} = \frac{{x + y + z}}{{a + b + c}}\)\( = \frac{{x + y + z}}{1} = x + y + z\) Ta có : \({\left( {x + y + z} \right)^2} = {\left( {\frac{x}{a}} \right)^2} = {\left( {\frac{y}{b}} \right)^2} = {\left( {\frac{z}{c}} \right)^2}\) \( = \frac{{{x^2}}}{{{a^2}}} = \frac{{{y^2}}}{{{b^2}}} = \frac{{{z^2}}}{{{c^2}}}\) \( = \frac{{{x^2} + {y^2} + {z^2}}}{{{a^2} + {b^2} + {c^2}}} = \frac{{{x^2} + {y^2} + {z^2}}}{1}\) \( = {x^2} + {y^2} + {z^2}\) Vậy \({\left( {x + y + z} \right)^2} = {x^2} + {y^2} + {z^2}\) (đpcm).
|