Đề kiểm tra giữa kì I Toán 7 - Đề số 6 có lời giải chi tiếtĐề kiểm tra giữa kì I Toán 7 - Đề số 6 có lời giải chi tiết Đề bài I. TRẮC NGHIỆM (1,5 điểm) Ghi lại chữ cái đứng trước câu trả lời đúng. Câu 1. Kết quả thực hiện phép tính (−0,5)2+34 là A. 14 B. 1 C. −12 D. 12 Câu 2. Kết quả thực hiện phép tính −38+14:2 là: A. 14 B. −116 C. −14 D. 12 Câu 3. Cho ΔABC có ˆA=50∘,ˆC=70∘. Góc ngoài của tam giác tại đỉnh B có số đo là A. 140∘ B. 100∘ C. 60∘ D. 120∘ II. TỰ LUẬN (8,5 điểm) Câu 1 (2 điểm). Thực hiện phép tính: a)25.1513−25.1013 b)(−23)0−15:√925+20% Câu 2 (2 điểm) Tìm x, biết: a)(x−1)3=−27 b)2−12|2x−1|=0,5 Câu 3 (2 điểm) Cho hình vẽ sau: Biết AB//DE,^BAC=1200,^CDE=1300. Tính: ^BAC+^ACD+^CDE. Câu 4 (2 điểm) Biết các cạnh của một tam giác tỉ lệ với 4; 5; 3 và chu vi của nó bằng 120m. Tính cạnh nhỏ nhất của tam giác đó. Câu 5 (0,5 điểm). Tìm các số a,b biết: |5a−6b+300|2011+(2a−3b)2010=0 . Lời giải chi tiết I. TRẮC NGHIỆM
Câu 1: Phương pháp: Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc: Lũy thừa → Nhân và chia → Cộng và trừ Cách giải: (−0,5)2+34=(−12)2+34 =14+34=44=1 Chọn B Câu 2: Phương pháp:Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc: Lũy thừa → Nhân và chia → Cộng và trừ Cách giải: −38+14:2=−38+14.2=−38+18=−28=−14 Chọn C Câu 3: Phương pháp: - Áp dụng định lí tổng ba góc trong tam giác để tìm tổng số đo góc B. - Áp dụng tính chất : Hai góc kề bù có tổng số đo bằng 180∘. Cách giải: Áp dụng định lí tổng ba góc trong tam giác ABC ta có: ˆA+ˆB+ˆC=180∘ ⇒ˆB=180∘−(ˆA+ˆC)=180∘−(50∘+70∘)=60∘ Vì góc ngoài tại đỉnh B và góc .. là hai góc kề bù nên có tổng số đo là 180∘. Suy ra góc ngoài của tam giác tại đỉnh B có số đo là 180∘−60∘=120∘. Chọn D II. TỰ LUẬN Câu 1: Phương pháp: Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc: Lũy thừa → Nhân và chia → Cộng và trừ Sử dụng tính chất phân phối của phép nhân đối với phép cộng, phép trừ Cách giải:
Câu 2: Phương pháp: a) Biến đổi −27=(−3)3 , sau đó áp dụng tính chất từ đó tìm x. b) Áp dụng quy tắc chuyển vế tìm được |2x−1|, sau đó áp dụng tính chất : |A|=B⇒A=B hoặc A=−B. Cách giải:
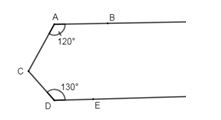
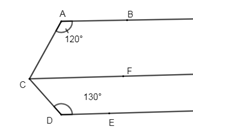
Câu 3: Phương pháp: Áp dụng tính chất hai đường thẳng song song, tiên đề Ơ-Clit. - Tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau. Cách giải: Kẻ CF//AB⇒^BAC+^ACF=1800 (2 góc trong cùng phía) ⇒^ACF=1800−^BAC=1800−1200=600 Ta có: {AB//DECF//AB(gt)⇒DE//CF. ⇒^FCD+^CDE=1800 (2 góc trong cùng phía) ⇒^DCF=1800−^CDE=1800−1300=500⇒^ACD=^ACF+^FCD=600+500=1100⇒^BAC+^ACD+^CDE=1200+1100+1300=3600 Câu 4: Phương pháp: Gọi các cạnh của tam giác là x;y;z(x;y;z>0). Sử dụng dữ kiện đề bài để suy ra tỉ lệ thức và sử dụng tính hất dãy tỉ số bằng nhau. Cách giải: Gọi các cạnh của tam giác là x;y;z(x;y;z>0) Theo đề bài ta có x4=y5=z3 và x+y+z=120. Áp dụng tính chất dãy tỉ số bằng nhau ta có x4=y5=z3=x+y+z4+5+3=12012=10 Do đó x=4.10=40m; y=5.10=50m; z=3.10=30m. Cạnh nhỏ nhất của tam giác dài 30m. Câu 5: Phương pháp: Áp dụng tính chất : |x|≥0 với mọi x∈Z và xn≥0 với mọi n là số chẵn. Cách giải: |5a−6b+300|2011+(2a−3b)2010=0|5a−6b+300|2011≥0⇒|5a−6b+300|2011≥0(2a−3b)2010≥0⇒|5a−6b+300|2011+(2a−3b)2010≥0Hay|5a−6b+300|2011+(2a−3b)2010=0khi{5a−6b+300=02a−3b=02a−3b=0⇒2a=3b⇒a3=b2=5a−6b3.5−2.6=−3003=−100⇒a=−300;b=−200
|