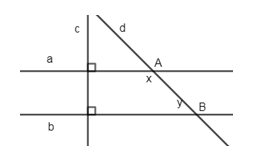
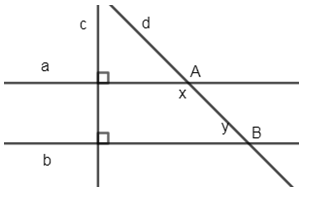
Đề kiểm tra giữa kì I Toán 7 - Đề số 3 có lời giải chi tiếtĐề kiểm tra giữa kì I Toán 7 - Đề số 3 có lời giải chi tiết Đề bài Bài 1 (2 điểm) a) Tính hợp lý: \(\frac{1}{4} + \frac{3}{4}.19\frac{1}{3} - \frac{3}{4}.39\frac{1}{3}\) b) Thực hiện phép tính: \(\left[ {\sqrt {\frac{4}{9}} + {{\left( { - \frac{1}{2}} \right)}^2}} \right]:0,75 + 1\frac{1}{3}.\left| {1 - \frac{{11}}{{12}}} \right|\) Bài 2 ( 3 điểm) Tìm .. biết: \(a)\,\,\frac{3}{4}x + \frac{1}{2} = 5\) \(b)\,\,1\frac{1}{4} - \left| {x + \frac{5}{6}} \right| = \frac{{ - 5}}{7}.\frac{{21}}{6}\) \(c)\,\,\left( {{x^2} + \sqrt {16} } \right)\left( {\left| x \right| - \frac{1}{3}} \right) = 0\) Bài 3 (2 điểm) Sàn nhà của bác An là hình chữ nhật có độ dài hai cạnh tỉ lệ với 3; 4 và chu vi là \(28\) mét. a) Tìm chiều dài hai cạnh của sàn nhà bác An. b) Bác An dự định mua gạch men để lát lại sàn nhà. Cửa hàng báo giá mỗi mét vuông gạch là 300.000 đồng. Em hãy tính xem số tiền phải trả để mua gạch men là bao nhiêu? Câu 4 (1 điểm): Tìm hai số \(x;y\) biết \(\frac{x}{3} = \frac{y}{5}\) và \(x + y = - 32\) Bài 5 ( 2 điểm): Cho hình vẽ sau: Biết \(a \bot c,\,b \bot c,\,2{\rm{x}} = 3y\). Tính x, y. Lời giải chi tiết Bài 1: Phương pháp: Nhóm các số hạng thích hợp để được tổng là số tròn trăm, tròn chục,… Thứ tự thực hiện phép tính: - Có ngoặc: trong ngoặc trước, ngoài ngoặc sau. - Không có ngoặc: Lũy thừa, nhân chia, công trừ. Cách giải:
Bài 2: Phương pháp: a) Áp dụng quy tắc chuyển vế đổi dấu. b) Sử dụng kiến thức: \(\left| A \right| = B > 0\) thì \(A = B\) hoặc \(A = - B\). c) Sử dụng kiến thức: \(AB = 0\) thì \(A = 0\) hoặc \(B = 0\). Cách giải:
\(c)\,\,\left( {{x^2} + \sqrt {16} } \right)\left( {\left| x \right| - \frac{1}{3}} \right) = 0\) \(\left( {{x^2} + 4} \right)\left( {\left| x \right| - \frac{1}{3}} \right) = 0\) TH1: \({x^2} + 4 = 0\) \(\begin{array}{l}{x^2} = 0 - 4\\{x^2} = - 4\end{array}\) Không có giá trị nào của \(x\) thỏa mãn vì \({x^2} \ge 0\) với mọi \(x\) và \( - 4 < 0\). TH2: \(\left| x \right| - \frac{1}{3} = 0\) \(\begin{array}{l}\left| x \right| = \frac{1}{3}\\x = \pm \frac{1}{3}\end{array}\) Vậy \(x = \pm \frac{1}{3}\). Bài 3: Phương pháp: a) Gọi chiều dài, chiều rộng là \(x,y\). Lập luận thiết lập mối quan hệ của \(x,y\) dựa vào điều kiện bài cho. Sử dụng tính chất của dãy tỉ số bằng nhau: \(\frac{a}{b} = \frac{c}{d} = \frac{{a + c}}{{b + d}}\). b) Tính diện tích mặt sàn, từ đó suy ra số tiền cần trả. Cách giải: a) Tìm chiều dài hai cạnh của sàn nhà bác An. Gọi chiều dài, chiều rộng sàn nhà lần lượt là \(x,y\) \(\left( {x > y > 0} \right)\). Nửa chu vi hình chữ nhật là: \(28:2 = 14\left( m \right)\). Do đó \(x + y = 14\). Vì hai cạnh tỉ lệ với \(3;4\) nên \(\frac{x}{4} = \frac{y}{3}\) (do \(x > y\)) Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\frac{x}{4} = \frac{y}{3} = \frac{{x + y}}{{4 + 3}} = \frac{{14}}{7} = 2\) \(\begin{array}{l} \Rightarrow x = 4.2 = 8\left( m \right)\\y = 3.2 = 6\left( m \right)\end{array}\) Vậy chiều rộng sàn nhà là \(6m\) và chiều dài sàn nhà là \(8m\). b) Bác An dự định mua gạch men để lát lại sàn nhà. Của hàng báo giá mỗi mét vuông gạch là 300.000 đồng. Em hãy tính xem số tiền phải trả để mua gạch men là bao nhiêu? Diện tích sàn nhà là: \(6.8 = 48\left( {{m^2}} \right)\). Số tiền phải trả là: \(48.300000 = 14400000\) (đồng) Vậy bác An phải trả \(14400000\) đồng mua gạch men. Câu 4: Phương pháp: Sử dụng tính chất dãy tỉ số bằng nhau. Cách giải: Áp dụng dãy tỉ số bằng nhau ta có: \(\frac{x}{3} = \frac{y}{5} = \frac{{x + y}}{{3 + 5}} = \frac{{ - 32}}{8} = - 4\) Do đó \(\frac{x}{3} = - 4 \Rightarrow x = - 12\) và \(\frac{y}{5} = - 4 \Rightarrow y = - 20.\) Vậy \(x = - 12;y = - 20.\) Câu 5: Phương pháp: Áp dụng tính chất hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. - Tính chất hai đường thẳng song song. Cách giải: Vì \(a \bot c,\,b \bot c\left( {gt} \right) \Rightarrow a//\,b \Rightarrow \widehat {aAB} + \widehat {ABb} = {180^0} \Rightarrow x + y = {180^0}\)(2 góc trong cùng phía bù nhau) \( \Rightarrow x = {180^0} - y\) Lại có: \(\begin{array}{l}2{\rm{x}} = 3y\left( {gt} \right) \Rightarrow 2\left( {{{180}^0} - y} \right) = 3y\\ \Leftrightarrow {360^0} - 2y = 3y\\ \Leftrightarrow 5y = {360^0} \Rightarrow y = {360^0}:5 = {72^0}\\ \Rightarrow x = {180^0} - {72^0} = {108^0}\end{array}\)
|