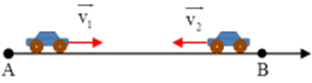
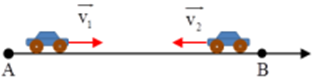
Đề kiểm tra giữa học kì 1 Vật lí 10 - Đề số 05 có lời giải chi tiết

Đề bài

PHẦN I – TRẮC NGHIỆM

Câu 1: Chọn đáp số đúng. Hai lực đồng quy có độ lớn là 9N và 12N. Giá trị nào có thể là độ lớn của hợp lực:

A. 25N                                   B. 1N 

C. 2N                                     D. 15N

Câu 2: Lúc 8h sáng, tại A xe thứ nhất chuyển động thẳng đều với tốc độ 20km/h để về B. Hai giờ sau, tại B xe thứ hai cũng chuyển động thẳng đều với tốc độ 30km/h theo chiều ngược lại để về A. Cho đoạn thẳng AB = 90km. Thời điểm hai xe gặp nhau là:

A. 3h                                      B. 2h

C. 1h                                      D. 4h

Câu 3: Một chiếc xe khối lượng 2 tấn đang chuyển động trên đường ngang với vận tốc 54km/h thì người lái xe hãm phanh. Chiếc xe chạy chậm dần đều được 20m thì dừng hẳn. Lực hãm có thể là:

A. 11250N                             B. 12250N

C. 20000N                             D. 1550N

Câu 4: Công thức nào dưới đây là công thức liên hệ giữa v, a và s:

A. $v - {v_0} = \sqrt {2a.s}$

B. $v + {v_0} = \sqrt {2a.s}$

C. ${v^2} - v_0^2 = 2a.s$

D. ${v^2} + v_0^2 = 2a.s$

Câu 5: Gọi ${F_1};{F_2}$ là độ lớn của hai lực thành phần, $F$ là độ lớn hợp lực của chúng. Câu nào sau đây đúng?

A. $F$ không bao giờ nhỏ hơn cả ${F_1}$ và ${F_2}$

B. Trong mọi trường hợp: $\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}$

C. $F$ luôn luôn lớn hơn cả ${F_1}$ và ${F_2}$

D. $F$ không bao giờ bằng ${F_1}$ hoặc ${F_2}$

Câu 6: Kim giờ của một đồng hồ dài 30cm, kim phút dài 40cm. Tỉ số tốc độ dài của điểm đầu kim giờ và

kim phút là:

A. $\frac{{{v_p}}}{{{v_h}}} = 12$

B. $\frac{{{v_p}}}{{{v_h}}} = 16$

C. $\frac{{{v_h}}}{{{v_p}}} = 16$

D. $\frac{{{v_h}}}{{{v_p}}} = 12$

Câu 7: Một vật được ném lên theo phương thẳng đứng từ mặt đất. Sau 6s vật lại rơi xuống mặt đất. Cho $g = 10m/{s^2}$.  Độ cao tối đa mà vật lên tới là:

A. 20m                                   B. 25m

C. 37m                                   D. 45m

Câu 8: Công thức liên hệ giữa tốc độ góc $\omega$ với chu kì T và tần số f là:

A. $\omega  = \frac{{2\pi }}{T};f = 2\pi \omega$

B. $T = \frac{{2\pi }}{\omega };f = 2\pi \omega$             

C. $T = \frac{{2\pi }}{\omega };\omega  = 2\pi f$

D. $\omega  = 2\pi f;\omega  = 2\pi T$

Câu 9: Chọn câu sai:

A. Chuyển động của người nhảy dù cũng là chuyển động rơi tự do.

B. Khi được coi là rơi tự do mọi vật chuyển động rơi giống nhau.

C. Vật rơi tự do không chịu sức cản của không khí.

D. Chuyển động rơi rự do là chuyển động nhanh dần đều.

Câu 10: Chọn đáp án đúng. Giả sử một vật đang trượt trên đường phẳng nhẵn mà đột nhiên mất hết các lực tác dụng vào vật thì:

A. vật sẽ chuyển động thẳng đều với vận tốc cũ

B. vật sẽ chuyển động chậm dần một thời gian rồi chuyển động tròn đều

C. vật chuyển động chậm dần rồi dừng lại

D. vật dừng lại ngay.

Câu 11: Một tàu thủy chở hàng đi xuôi dòng sông trong 4 giờ đi được 100 km, khi chạy ngược dòng trong 4 giờ thì đi được 60 km. Tính vận tốc của tàu so với nước. Coi vận tốc của nước đối bờ là luôn luôn không đổi.

A. 5km/h                                B. 10km/h

C. 15km/h                              D. 20km/h

Câu 12: Một ôtô chuyển động từ A về B. Chặng đầu xe đi mất $\frac{1}{3}$ tổng thời gian với vận tốc ${v_1}\; = 45km/h$. Chặng giữa xe đi mất  $\frac{1}{2}$ tổng thời gian với vận tốc ${v_2}\; = 60km/h$. Chặng còn lại xe chuyển động với vận tốc ${v_3}\; = 48km/h$. Tính vận tốc của xe trên cả quãng đường AB.

A. $v = 40km/h$

B. $v = 53km/h$

C. $v = 46km/h$

D. $v = 54km/h$

Câu 13: Cùng một lúc tại hai điểm A, B cách nhau 125m có hai vật chuyển động ngược chiều nhau. Vật đi từ A có vận tốc đầu 4 m/s và gia tốc là $2m/{s^2}$,  vật đi từ B có vận tốc đầu 6 m/s và gia tốc$4m/{s^2}$.  Biết các vật chuyển động nhanh dần đều. Chọn A làm gốc tọa độ, chiều dương hướng từ A đến B, gốc thời gian lúc hai vật cùng xuất phát. Xác định thời điểm hai vật gặp nhau?

A. 10s                                     B. 5s

C. 6s                                       D. 12s

Câu 14: Một vật chuyển động nhanh dần đều với vận tốc ban đầu bằng  0.  Trong giây thứ nhất, vật đi được quãng đường  s = 3m.  Trong giây thứ hai, vật đi được quãng đường bao nhiêu?

A. 9m                        B. 3m

C. 6m                        D. Đáp án khác

Câu 15: Thả một hòn đá từ độ cao $h$ xuống đất và hòn đá rơi trong $1s$. Nếu thả hòn đá từ độ cao  thì thời gian rơi là:

A. 5s                                       B. 1s

C. 2s                                       D. 4s

Câu 16: Một vệ tinh nhân tạo chuyển động tròn đều quanh Trái Đất, mỗi vòng hết 90 phút. Vệ tinh bay ở độ cao 320 km so với mặt đất. Biết bán kính Trái Đất là 6380 km. Vận tốc và gia tốc hướng tâm của vệ tinh là:

A. $7792m/s;{\rm{ }}9,062{\rm{ }}m/{s^2}$

B. $7651m/s;{\rm{ }}8,120{\rm{ }}m/{s^2}$

C. $6800m/s;{\rm{ }}7,892{\rm{ }}m/{s^2}$

D. $7902m/s;{\rm{ }}8,960{\rm{ }}m/{s^2}$

Câu 17: Hãy chỉ ra câu không đúng.

A. Quỹ đạo của chuyển động thẳng đều là đường thẳng.

B. Tốc độ trung bình của chuyển động thẳng đều trên mọi đoạn đường là như nhau.

C. Trong chuyển động thẳng đều, quãng đường đi được của vật tỉ lệ thuận với khoảng thời gian chuyển động.

D. Chuyển động đi lại của một pit-tông trong xilanh là chuyển động thẳng đều.

Câu 18: Trong phương án thực nghiệm đo gia tốc rơi tự do tại một phòng thí nghiệm của trường THPT, người ta đặt cổng quang điện cách nam châm điện một khoảng $s = 0,5m$ và đo được khoảng thời gian rơi của vật là 0,32s. Gia tốc rơi tự do tính được từ thí nghiệm trên là:

A. $g = 9,81m/{s^2}$

B. $g = 10,0m/{s^2}$

C. $g = 9,76m/{s^2}$

D. $g = 10,1m/{s^2}$

Câu 19: Một quạt máy quay với tần số  400 vòng/ phút. Cách quạt dài 0,8m.  Tính tốc độ dài và tốc độ góc của một điểm ở đầu cánh quạt.

A. $\omega  = 33,5rad/s;\,\,v = 41,87m/s$

B. $\omega  = 41,87rad/s;v = 33,5m/s$

C. $\omega  = 33,5m/s;{\mkern 1mu} {\mkern 1mu} v = 41,87rad/s$

D. $\omega  = 41,87m/s;v = 33,5rad/s$

Câu 20: Một em bé ngồi trên ghế của một chiếc đu quay đang quay với tần số  5 vòng/phút. Khoảng cách từ chỗ người ngồi đến trục quay của chiếc đu là 3m.  Gia tốc hướng tâm của em bé đó là bao nhiêu?

A. ${a_{ht}} = 8,2{\mkern 1mu} {\mkern 1mu} m/{s^2}$

B. ${a_{ht}} = 2,{96.10^2}{\mkern 1mu} {\mkern 1mu} m/{s^2}$

C. ${a_{ht}} = 29,{6.10^2}{\mkern 1mu} {\mkern 1mu} m/{s^2}$

D. ${a_{ht}} = 0,82{\mkern 1mu} {\mkern 1mu} m/{s^2}$

PHẦN II – TỰ LUẬN

Bài 1: Hai xe chuyển động ngược chiều nhau trên cùng một đường thẳng từ hai địa điểm A và B cách nhau 400m.  Lúc  6  giờ xe thứ nhất qua A với tốc độ ${v_1} = 20m/s$,  ngay sau đó xe tắt máy chuyển động chậm dần đều với gia tốc $2m/{s^2}$.  Cùng lúc đó xe thứ 2 qua B chuyển động thẳng đều với tốc độ ${v_2} = 72km/h$. Chọn trục Ox trùng đường thẳng AB, gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian là lúc 6 giờ.

a, Viết phương trình chuyển động của xe thứ nhất. Xác định quãng đường đi và vận tốc của xe sau  5  giây.

b, Viết phương trình chuyển động của xe thứ hai. Xác định vị trí của xe sau hai 1 phút.

c, Tính thời gian chuyển động của xe thứ nhất đến khi dừng.

d, Xác định chính xác thời điểm và vị trí 2 xe gặp nhau.

Bài 2: Lực  $\overrightarrow F$ truyền cho vật khối lượng ${m_1}$  gia tốc , truyền cho vật khối lượng ${m_2}$ gia tốc Lực $\overrightarrow F$  sẽ truyền cho vật khối lượng $m = {m_1} - {m_2}\;$ gia tốc bao nhiêu?

Bài 3: Hai thành phố A và B cách nhau 100km. Cùng một lúc, hai xe chuyển động đều ngược chiều nhau, xe ô tô đi từ A với vận tốc 30km/h, xe ô tô đi từ B với vận tốc 20km/h. Chọn A làm gốc toạ độ, chiều dương từ A đến B, gốc thời gian là lúc hai xe bắt đầu đi.

a) Viết phương trình chuyển động của mỗi xe

b) Vẽ đồ thị toạ độ của mỗi xe. Từ đồ thị, xác định vị trí và thời điểm hai xe gặp nhau.

Lời giải chi tiết

1.D	2.A	3.A	4.C	5.B	6.B	7.D	8.C	9.A	10.A
11.D	12.B	13.B	14.A	15.C	16.A	17.D	18.C	19.B	20.D

Câu 1:

Phương pháp giải:

 

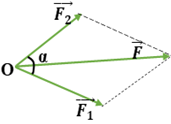
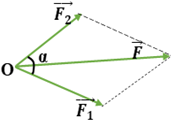
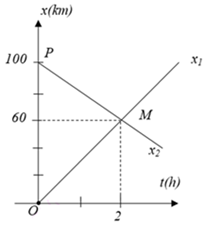
Áp dụng quy tắc hình bình hành: $\vec F = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}$

Độ lớn của hợp lực: $F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha }$

Vì ${0^0}\; \le \alpha  \le {180^0}\; \Rightarrow \left| {{F_1}\; - {F_2}} \right| \le F \le {F_1}\; + {F_2}$

Lời Giải:

Công thức xác định độ lớn của hợp lực : $F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha }$

Ta có :  $\left| {{F_1}\; - {F_2}} \right| \le F \le {F_1}\; + {F_2} \Leftrightarrow 3 \le F \le 21$

$\Rightarrow$ Vậy 15N là giá trị có thể là độ lớn của hợp lực

Chọn D.

Câu 2:

Phương pháp giải:

Phương trình chuyển động của chuyển động thẳng đều: $x = {x_0} + v\left( {t - {t_0}} \right)$

Hai xe gặp nhau: ${x_1} = {x_2} \Rightarrow t$

Lời Giải:

Chọn gốc tọa độ tại A, chiều dương chọn là chiều từ A hướng B. Chọn gốc thời gian là lúc hai xe bắt đầu khởi hành.

Phương trình của xe đi từ A có dạng: ${x_1} = {x_{01}} + {v_1}\left( {t - {t_{01}}} \right)$

Với:  $\left\{ {\begin{array}{*{20}{l}}{{x_{01}} = 0}\\{{t_{01}} = 0}\\{{v_1} = 20km/h}\end{array}} \right. \\\Rightarrow {x_1} = 0 + 20\left( {t - 0} \right) = 20t\left( {km} \right)$

Phương trình của xe đi từ B có dạng ${x_2} = {x_{02}} - {v_2}\left( {t - {t_{02}}} \right)$

Với:  $\left\{ {\begin{array}{*{20}{l}}{{x_{02}} = 90km}\\{{t_{02}} = 2}\\{{v_2} =  - 30km/h}\end{array}} \right. \\\Rightarrow {x_2} = 90 - 30\left( {t - 2} \right) = 150 - 30t\left( {km} \right)$

Hai xe gặp nhau khi: ${x_1} = {x_2} \Leftrightarrow 20t = 150 - 30t \Rightarrow t = 3h$

Chọn A.

Câu 3:

Phương pháp giải:

+ Công thức liên hệ giữa s, v và a: ${v^2} - v_0^2 = 2a.s \Rightarrow a = \frac{{{v^2} - v_0^2}}{{2s}}$

+ Định luật II Niu – tơn: Gia tốc của một vật cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật.

Hệ thức: $\vec a = \frac{{\vec F}}{m}$ hay $\vec F = m.\vec a$

Lời Giải:

Ta có: $\left\{ \begin{array}{l}m = 2T = 2000kg\\\begin{array}{*{20}{l}}{{v_0} = 54km/h = 15m/s}\\{v = 0}\\{s = 20m}\end{array}\end{array} \right.$

Gia tốc của xe: $a = \frac{{{v^2} - v_0^2}}{{2s}} = \frac{{{0^2} - {{15}^2}}}{{2.20}} =  - 5,625m/{s^2}$

Độ lớn hợp lực hãm là: ${F_h} = m\left| a \right| = 2000.5,625 = 11\,250N$

Chọn A.

Câu 4:

Công thức liên hệ giữa v, a và s là: ${v^2} - v_0^2 = 2a.s$

Chọn C.

Câu 5:

Phương pháp giải:

 

Áp dụng quy tắc hình bình hành: $\vec F = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}$

Độ lớn của hợp lực: $F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha }$

Vì ${0^0}\; \le \alpha  \le {180^0}\; \Rightarrow \left| {{F_1}\; - {F_2}} \right| \le F \le {F_1}\; + {F_2}$

Lời Giải:

Ta có: $\vec F = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}$

Độ lớn của hợp lực: $F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha }$

$\; \Rightarrow \left| {{F_1}\; - {F_2}} \right| \le F \le {F_1}\; + {F_2}$
Chọn B.

Câu 6:

Phương pháp giải:

Công thức tính tốc độ dài: $v = \omega .R = \frac{{2\pi }}{T}.R$

Lời Giải:

Ta có: $\left\{ \begin{array}{l}{T_h} = 12h\\{T_p} = 1h\\{R_h} = 30cm\\{R_p} = 40cm\end{array} \right.$

Lại có: $\left\{ \begin{array}{l}{v_p} = \frac{{2\pi }}{{{T_p}}}.{R_p}\\{v_h} = \frac{{2\pi }}{{{T_h}}}.{R_h}\end{array} \right.\\ \Rightarrow \frac{{{v_p}}}{{{v_p}}} = \frac{{{T_h}.{R_p}}}{{{T_p}.{R_h}}} = \frac{{12.40}}{{1.30}} = 16$

Chọn B.

Câu 7:

Phương pháp giải:

+ Ném lên tương đương với chuyển động thẳng chậm dần đều với gia tốc $- g$

Ném xuống tương đương với chuyển động thẳng nhanh dần đều với gia tốc $g$

+ Phương trình chuyển động: $y = {y_0} + {v_0}t + \frac{1}{2}a{t^2}$

+ Hai vật gặp nhau khi tọa độ của chúng bằng nhau: ${y_1} = {y_2}$

+ Công thức độc lập thời gian: ${v^2} - v_0^2 = 2as$

Lời Giải:

Chọn chiều dương hướng lên, gốc tọa độ tại mặt đất, gốc thời gian là lúc ném vật.

Chuyển động của vật ném lên thẳng đứng là chuyển động thẳng chậm dần đều với gia tốc:

 $a =  - g =  - 10m/{s^2}$ với vận tốc ban đầu ${v_0}$

Phương trình chuyển động của vật là: $y = {v_0}t - \frac{1}{2}g{t^2} = {v_0}t - 5{t^2}{\mkern 1mu} \left( m \right)$

Khi vật chạm đất thì: $\left\{ {\begin{array}{*{20}{l}}{y = 0}\\{t = 6s}\end{array}} \right. \Rightarrow {v_0}.6 - {5.6^2} = 0 \Rightarrow {v_0} = 30m/s$

Ta có: ${v^2} - v_0^2 = 2as \Rightarrow s = \frac{{{v^2} - v_0^2}}{{2a}}$

Khi vật đạt độ cao tối đa thì $v = 0 \Rightarrow s = \frac{{{0^2} - {{30}^2}}}{{2.\left( { - 10} \right)}} = 45m$

Chọn D.

Câu 8:

Phương pháp giải:

+ Công thức liên hệ giữa chu kì và tốc độ góc: $T = \frac{{2\pi }}{\omega }$

+ Công thức liên hệ giữa chu kì và tần số: $f = \frac{1}{T}$

Lời Giải:

Công thức liên hệ giữa tốc độ góc $\omega$ với chu kì T và tần số f là: $\left\{ \begin{array}{l}T = \frac{{2\pi }}{\omega }\\\omega  = 2\pi f\end{array} \right.$

Chọn C.

Câu 9:

Phương pháp giải:

+ Sự rơi tự do là sự rơi chỉ dưới tác dụng của trọng lực.

+ Trong trường hộ có thể bỏ qua ảnh hưởng của các yếu tố khác lên vật rơi, ta có thể coi sự rơi của vật như là sự rơi tự do.

+ Chuyển động rơi tự do là chuyển động thẳng nhanh dần đều theo phương thẳng đứng, chiều từ trên xuống dưới.

Lời Giải:

Chuyển động của người nhảy dù không phải là chuyển động rơi tự do.

Chọn A.

Câu 10:

Phương pháp giải:

Định luật I Niuton: Nếu không chịu tác dụng của lực nào hoặc chịu tác dụng của các lực có hợp lực bằng không, thì vật đang đứng yên sẽ tiếp tục đứng yên, đang chuyển động sẽ tiếp tục chuyển động thẳng đều.

Lời Giải:

Giả sử một vật đang trượt trên đường phẳng nhẵn mà đột nhiên mất hết các lực tác dụng vào vật thì vật sẽ chuyển động thẳng đều với vận tốc cũ.

Chọn A.

Câu 11:

Phương pháp giải:

Vật (1) : Vật chuyển động

Vật (2): Hệ quy chiếu chuyển động

Vật (3): Hệ quy chiếu đứng yên.

Ta có:

 + $\overrightarrow {{v_{12}}}$: vận tốc của vật chuyển động (1) so với hệ quy chiếu chuyển động (2) → Vận tốc tương đối

 + $\overrightarrow {{v_{13}}}$: vận tốc của vật chuyển động (1) so với hệ quy chiếu đứng yên (3) → Vận tốc tuyệt đối

 + $\overrightarrow {{v_{23}}}$: vận tốc của hệ quy chiếu chuyển động (2) so với hệ quy chiếu chuyển động (3) → Vận tốc kéo theo.

Công thức cộng vận tốc: $\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}}$

Lời Giải:

Vật (1): Tàu thuỷ; Vật (2): dòng nước; Vật (3): bờ sông.

Với  $\overrightarrow {{v_{12}}} {\mkern 1mu}$  là vận tốc của tàu so với nước; ${\mkern 1mu} {\mkern 1mu} \overrightarrow {{v_{23}}}$ là vận tốc của nước so với bờ.

Thời gian chuyển động là: $t = \frac{{AB}}{{{v_{13}}}}$

+ Tàu đi xuôi dòng ta có  $\overrightarrow {{v_{12}}} {\mkern 1mu}  \uparrow  \uparrow {\mkern 1mu} {\mkern 1mu} \overrightarrow {{v_{23}}}$

Vận tốc của tàu so với bờ là: ${v_{13}} = {v_{12}} + {v_{23}}$

mà ${v_{13}} = \frac{{{S_1}}}{{{t_x}}} = \frac{{100}}{4} = 25km/h\\ \Rightarrow {v_{12}} + {v_{23}} = 25{\mkern 1mu} {\mkern 1mu} \left( {km/h} \right){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( * \right)$

+ Tàu đi ngược dòng ta có: $\overrightarrow {{v_{12}}} {\mkern 1mu}  \uparrow  \downarrow {\mkern 1mu} {\mkern 1mu} \overrightarrow {{v_{23}}}$  

Vận tốc của tàu so với bờ là: ${v_{13}}' = {v_{12}} - {v_{23}}$

mà ${v_{13}}^\prime  = \frac{{{S_2}}}{{{t_x}}} = \frac{{60}}{4} = 15km/h \\\Rightarrow {v_{12}} - {v_{23}} = 15{\mkern 1mu} {\mkern 1mu} \left( {km/h} \right){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {**} \right)$

Từ (*) và (**) ta có $\left\{ {\begin{array}{*{20}{l}}{{v_{12}} + {v_{23}} = 25}\\{{v_{12}} - {v_{23}} = 15}\end{array}} \right.{\mkern 1mu}  \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{v_{12}} = 20km/h}\\{{v_{23}} = 5km/h}\end{array}} \right.$

$\Rightarrow$  Vận tốc của tàu so với nước là ${v_{12}}\; = 20km/h$

Chọn D.

Câu 12:

Phương pháp giải:

Vận tốc trung bình: ${v_{tb}} = \frac{{{S_1} + {S_2} + {S_3}}}{{{t_1} + {t_2} + {t_3}}}$

Công thức liên hệ giữa s,v, t: $S = v.t$

Lời Giải:

Gọi t là tổng thời gian xe chuyển động từ A về B, v là vận tốc trung bình của xe.

Thời gian xe đi hết chặng cuối là: $t - \frac{t}{3} - \frac{t}{2} = \frac{t}{6}$

Độ dài quãng đường AB là: $S = v.t\;{\rm{ }}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)$

Theo bài ta có: $S = {v_1}.\frac{t}{3} + {v_2}.\frac{t}{2} + {v_3}.\frac{t}{6}\\ = 45.\frac{t}{3} + 60.\frac{t}{2} + 48\frac{t}{6} = 53t{\mkern 1mu} {\mkern 1mu} \,\,{\mkern 1mu} (2)$

Từ (1) và (2) suy ra: $v.t = 53t \Rightarrow v = 53km/h$

Chọn B.

Câu 13:

Phương pháp giải:

+ Phương trình chuyển động thẳng biến đổi đều: $x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}$

+ Viết phương trình chuyển động của 2 vật

+ Hai xe gặp nhau khi: ${x_1} = {x_2} \Rightarrow t$

Lời Giải:

 

Chọn A làm gốc tọa độ, chiều dương hướng từ A đến B, gốc thời gian lúc hai vật cùng xuất phát

+ Phương trình chuyển động của hai vật lúc này là:

$\left\{ {\begin{array}{*{20}{l}}{{x_1} = 4t + {t^2}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( m \right)}\\{{x_2} = 125 - 6t - 2{t^2}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( m \right)}\end{array}} \right.$
+ Khi hai vật gặp nhau:

$\begin{array}{*{20}{l}}{{x_1} = {x_2} \Leftrightarrow 4t + {t^2} = 125 - 6t - 2{t^2}}\\{ \Leftrightarrow 3{t^2} + 10t - 125 = 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{t = 5{\rm{s}}}\\{t =  - \frac{{25}}{3} < 0{\mkern 1mu} {\mkern 1mu} (L)}\end{array}} \right.}\end{array}$

Vậy thời điểm 2 vật gặp nhau là $5s$

Chọn B.

Câu 14:

Phương pháp giải:

+ Công thức tính quãng đường đi được của chuyển động thẳng biến đổi đều: $s = {v_0}.t + \frac{1}{2}.a.{t^2}$

+ Quãng đường đi trong giây thứ n là: $\Delta s = {s_n} - {s_{n - 1}}$

Lời Giải:

Quãng đường vật đi được trong giây thứ nhất là 3m, ta có:

${s_1} = {v_0}{t_1} + \frac{1}{2}at_1^2 \Leftrightarrow 0.1 + \frac{1}{2}a{.1^2} = 3 \\\Rightarrow a = 6m/{s^2}$

Quãng đường vật đi được trong  2s  đầu là: 

${s_2} = 0.2 + \frac{1}{2}\left( 6 \right){.2^2} = 12m$

Quãng đường vật đi được trong giây thứ hai:

$\;s = {s_2} - {s_1} = 12 - 3 = 9m$

Chọn A.

Câu 15:

Phương pháp giải:

Công thức tính độ cao thả vật: $h = \frac{1}{2}g.{t^2}$

Lời Giải:

Ta có:  $\left\{ \begin{array}{l}h = \frac{1}{2}g.{t^2}\\h' = \frac{1}{2}g.t{'^2} = 4h\end{array} \right. \\\Rightarrow \frac{{t'}}{t} = \sqrt {\frac{{h'}}{h}}  = \sqrt 4  = 2 \Rightarrow t' = 2t = 2.1 = 2s$

Chọn C.

Câu 16:

Phương pháp giải:

Gia tốc hướng tâm: ${a_{ht}} = \frac{{{v^2}}}{r} = {\omega ^2}r$

Tốc độ dài: $v = \omega r = \frac{{2\pi }}{T}.r$

Lời Giải:

Chu kì: $T = 90{\rm{ }}ph = 5400s$

Có: $r = 6380 + 320 = 6700km = 6\,700{\rm{ }}000m$

Vận tốc:  $v = \omega r = \frac{{2\pi }}{T}.r = \frac{{2.3,14}}{{5400}}.6700000 \approx 7792m/s$

Gia tốc hướng tâm: ${a_{ht}} = \frac{{{v^2}}}{r} = \frac{{{{7792}^2}}}{{6700000}} \approx 9,062m/{s^2}$

Chọn A.

Câu 17:

Phương pháp giải:

Sử dụng lí thuyết về:

- Chuyển động thẳng đều là chuyển động có quĩ đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.

- Công thức tính quãng đường đi được trong chuyển động thẳng đều: $s = vt \Rightarrow s \sim t$

Lời Giải:

+ A, B - đúng vì chuyển động thẳng đều là chuyển động có quĩ đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.

+ C - đúng vì quãng đường đi được trong chuyển động thẳng đều là $s = vt \Rightarrow s\sim t$

+ D - sai vì chuyển động đi lại của một pit-tông trong xilanh có quĩ đạo là đường thẳng nhưng có tốc độ trung bình không như nhau trên mọi quãng đường.

Chọn D.

Câu 18:

Phương pháp giải:

Công thức tính quãng đường đi được của vật rơi tự do: $s = \frac{1}{2}g{t^2} \Rightarrow g = \frac{{2s}}{{{t^2}}}$

Lời Giải:

Ta có: $\left\{ \begin{array}{l}s = 0,5m\\t = 0,32s\end{array} \right.$

$\Rightarrow$ Gia tốc rơi tự do tính được từ thí nghiệm trên là: $g = \frac{{2s}}{{{t^2}}} = \frac{{2.0,5}}{{0,{{32}^2}}} = 9,765625m/{s^2}$

Chọn C.

Câu 19:

Phương pháp giải:

+ Tốc độ góc $\omega  = 2\pi f$

+ Tốc độ dài: $v = \omega .r$

Lời Giải:

Ta có:

 + Tần số: $f = 400vong/phut = \frac{{20}}{3}vong/s$

 + Bán kính: $r = 0,8m$

Tốc độ góc của một điểm bất kì ở đầu cánh quạt là:

$\omega  = 2\pi f = 2\pi .\frac{{20}}{3} = 41,87rad/s$

Tốc độ dài của điểm trên đầu cánh quạt là: 

$v = r.\omega  = 0,8.41,87{\mkern 1mu} \,{\rm{ =  33}},{\rm{5}}m/s$

Chọn B.

Câu 20:

Phương pháp giải:

Công thức tính gia tốc hướng tâm  là: ${a_{ht}} = \frac{{{v^2}}}{r} = {\omega ^2}r$

Công thức liên hệ giữa tần số và tốc độ góc: $\omega  = 2\pi f$

Lời Giải:

Tần số: $f = 5vong/phut = \frac{1}{{12}}vong/s$

Tốc độ góc của chuyển động tròn đều là: $\omega  = 2\pi .f = 2\pi .\frac{1}{{12}} = \frac{\pi }{6}rad/s$

Gia tốc hướng tâm của em bé đó là: ${a_{ht}} = {\omega ^2}r = {\left( {\frac{\pi }{6}} \right)^2}.3 \approx 0,82m/{s^2}$

Chọn D.

PHẦN II – TỰ LUẬN

Bài 1:

Phương pháp giải:

+ Phương trình chuyển động thẳng biến đổi đều: $x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}$

+ Công thức tính vận tốc của vật chuyển động thẳng biến đổi đều: $v = {v_0} + at$

+ Công thức tính quãng đường đi được của chuyển động thẳng biến đổi đều: $s = {v_0}t + \frac{1}{2}a{t^2}$

+ Phương trình của chuyển động thẳng đều: $x = {x_0} + vt$

+ Viết phương trình chuyển động của 2 xe

+ Hai xe gặp nhau khi: ${x_1} = {x_2}$

+ Thay $t$  vào phương trình của 1 xe

Lời Giải:

Chọn trục Ox trùng đường thẳng AB, gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian là lúc  6  giờ.

a) Phương trình chuyển động của xe qua thứ nhất (đi từ A sang B ) là:

${x_1} = {x_{01}} + {v_{01}}.t + \frac{1}{2}{a_1}.{t^2} = 20t - {t^2}{\mkern 1mu} {\mkern 1mu} \left( m \right){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\left( 1 \right)$

Công thức tính vận tốc và quãng đường đi được: $\left\{ {\begin{array}{*{20}{c}}{{v_1} = 20 - 2t{\mkern 1mu} {\mkern 1mu} \left( {m/s} \right){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\,\left( 2 \right)}\\{{s_1} = 20t - {t^2}{\mkern 1mu} {\mkern 1mu} \left( m \right){\mkern 1mu} {\mkern 1mu} \,\,\,\,\,\,\,\,{\mkern 1mu} \left( 3 \right)}\end{array}} \right.$

Vậy sau  5s  thì: $\left\{ {\begin{array}{*{20}{c}}{{v_1} = 20 - 2.5 = 10{\mkern 1mu} {\mkern 1mu} \left( {m/s} \right)}\\{{s_1} = 20.5 - {5^2} = 75{\mkern 1mu} {\mkern 1mu} \left( m \right)}\end{array}} \right.$

b) Đổi ${v_{02}} = 72km/h = 20m/s$

Phương trình chuyển động của xe thứ hai là: ${x_2} = {x_{02}} - {v_{02}}.t = 400 - 20t{\mkern 1mu} {\mkern 1mu} \,\,\left( 4 \right)$

Sau $1ph = 60s\;$ thì vị trí của xe 2 là: ${x_2} = 400 - 20.60 =  - 800\left( m \right)$

Tức là xe thứ hai đã đi qua A được  800m.

c) Xe thứ nhất khi dừng lại có vận tốc bằng 0.  Thay vào phương trình (2) ta có:

${v_1} = 0 \Leftrightarrow 20 - 2t = 0 \Rightarrow t = 10s$

d) Sau  10s  thì xe thứ nhất dừng lại, nên vị trí của xe thứ nhất khi đó là: ${x_1} = 20.10 - {10^2} = 100m$

Sau đó dù thời gian trôi đi, xe 1 vẫn đứng yên tại đó, ta chỉ cần xác định thời gian xe 2 đi qua vị trí này.  

${x_2} = 100m \Leftrightarrow 400 - 20t = 100{\mkern 1mu} {\mkern 1mu}  \Rightarrow t = 15s$

Vậy thời điểm hai xe gặp nhau là: $6h + 15s = 6h0ph15s$

Vị trí gặp nhau cách A  100m.

Bài 2:

Phương pháp giải:

Định luật II Niu – tơn: Gia tốc của một vật cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật.

$\vec a = \frac{{\vec F}}{m}$ hay $\vec F = m.\vec a$

 Lời Giải:

Ta có:  $\left\{ {\begin{array}{*{20}{l}}{{a_1} = \frac{F}{{{m_1}}} \Rightarrow {m_1} = \frac{F}{{{a_1}}}}\\{{a_2} = \frac{F}{{{m_2}}} \Rightarrow {m_2} = \frac{F}{{{a_2}}}}\\{a = \frac{F}{{\left( {{m_1} - {m_2}} \right)}} \Rightarrow {m_1} - {m_2} = \frac{F}{a}}\end{array}} \right.$

$\Rightarrow \frac{F}{{{a_1}}} - \frac{F}{{{a_2}}} = \frac{F}{a} \Leftrightarrow \frac{1}{{{a_1}}} - \frac{1}{{{a_2}}} = \frac{1}{a} \\\Leftrightarrow \frac{1}{a} = \frac{1}{2} - \frac{1}{6} = \frac{1}{3} \Rightarrow a = 3m/{s^2}$

Bài 3:

Phương pháp giải:

+ Phương trình chuyển động của chuyển động thẳng đều: $x = {x_0} + vt$

+ Ôn tập lại cách vẽ đồ thị của hàm số: $y = a.x + b$ trong môn Toán.

Lời Giải:

 

a)  Phương trình chuyển động của hai xe:

Xe ô tô đi từ A: ${x_{1\;}} = 30t\,\,\left( {km} \right)$

Xe ô tô đi từ B: ${x_2}\; = 100 - 20t\,\,\,\left( {km} \right)$

b) Đồ thị toạ độ-thời gian của hai xe:

Hai đường thẳng cắt nhau tại điểm M nên

vị trí 2 xe gặp nhau cách gốc tọa độ 60km,

thời điểm hai xe gặp nhau là lúc 2h.

HocTot.Nam.Name.Vn