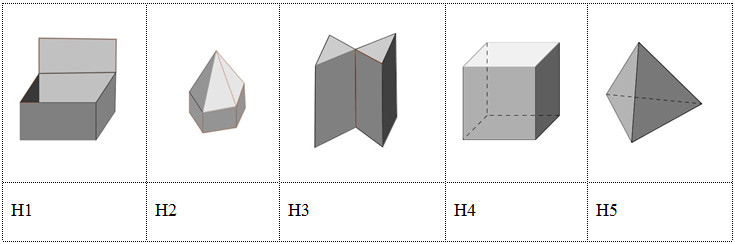
Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương I - Hình học 12

Đề bài

Câu 1: Một hình chóp có 28 cạnh sẽ có bao nhiêu mặt?

A. 14               B. 28   

C. 15              D. 42

Câu 2. Những hình nào không phải là khối đa diện?

A.  H1 và H3.             B. H1 và H2. 

C. H2 và H4.              D. H3 và H5.

Câu 3: Cho khối chóp S.ABC. Lấy A', B' lần lượt thuộc SA, SB sao cho 2SA' = 3A'A; 3SB' = B'B. Tỉ số thể tích giữa hai khối chóp S.A'B'C và S.ABC là:

A. $\dfrac{3}{{20}}$ ,            B.$\dfrac{2}{{15}}$ ,

C.$\dfrac{1}{6}$ ,               D. $\dfrac{3}{{10}}$

Câu 4: thể tích của khối hộp chữ nhật ABCDA’B’C’D’ có AB = a; BC = b; AA’ = c là:

A. $V = ab+bc+ca$       B. $V = b^3$

C. $V = c^3$                   D. $V = abc$

Câu 5: Cho khối lăng trụ ABC.A’B’C’ có thể tích là V. Thể tích của khối chóp A’.ABC là:

A. 2V              B. $\dfrac{1}{2}V$

C. $\dfrac{1}{3}V$           D. $\dfrac{1}{6}V$

Câu 6: Số đỉnh của một hình bát diện đều là:

A. Sáu           B. Tám

C. Mười        D. Mười hai

Câu 7: Khối chóp có diện tích đáy 4 $m^2$ và chiều cao 1,5m có thể tích là:

A. $6 m^3$             B. $4.5{m^3}$

C. $4{m^3}$             D. $2 m^3$

Câu 8: Khối chóp tứ giác đều có thể tích $V = 2{{\rm{a}}^3}$, cạnh đáy bằng $a\sqrt 6$ thì chiều cao khối chóp bằng:

A. a.       B. $a\sqrt 6$

C. $\dfrac{a}{3}$      D. $\dfrac{{a\sqrt 6 }}{3}$

Câu 9. Cho khối chóp $S.ABC$có đáy $ABC$ là tam giác đều cạnh $a$. Hai mặt bên $\left( {SAB} \right)$ và $\left( {SAC} \right)$ cùng vuông góc với đáy. Tính thể tích khối chóp biết $SC = a\sqrt 3$

A. $\dfrac{{2{a^3}\sqrt 6 }}{9}$    B. $\dfrac{{{a^3}\sqrt 6 }}{{12}}$            

C. $\dfrac{{{a^3}\sqrt 3 }}{4}$       D. $\dfrac{{{a^3}\sqrt 3 }}{2}$

Câu 10. Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a biết  SA   vuông góc với đáy ABC và (SBC) hợp với đáy (ABC) một góc $60^o$.   Tính thể tích hình chóp

A. $\dfrac{{{a^3}\sqrt 3 }}{8}$            B. $\dfrac{{{a^3}\sqrt 3 }}{{12}}$

C. $\dfrac{{{a^3}}}{4}$                  D. $\dfrac{{{a^3}\sqrt 3 }}{4}$

Câu 11. Cho khối chóp $S.ABCD$có đáy $ABCD$ là hình chữ nhật $AD = 2a,\,AB = a$. Gọi $H$ là trung điểm của $AD$ , biết $SH \bot \left( {ABCD} \right)$. Tính thể tích khối chóp biết $SA = a\sqrt 5$.

A. $\dfrac{{2{a^3}\sqrt 3 }}{3}$          B. $\dfrac{{4{a^3}\sqrt 3 }}{3}$

C. $\dfrac{{4{a^3}}}{3}$                D. $\dfrac{{2{a^3}}}{3}$

Câu 12.  Cho hình chóp tứ giác  có đáy là hình chữ nhật cạnh  các cạnh bên có độ dài bằng nhau và bằng . Thể tích khối chóp  bằng:

$A.\,\,\dfrac{{10{a^3}}}{{\sqrt 3 }}$           $B.\,\,\dfrac{{9{a^3}\sqrt 3 }}{2}$

$C.\,\,10{a^3}\sqrt 3$        $D.\,\,9{a^3}\sqrt 3$

Câu 13.  Tổng diện tích các mặt của một hình lập phương bằng $216.$ Thể tích của khối lập phương đó là:

A.216               B.36 

C. 125              D. Đáp án khác

Câu 14: Cho hình chóp đều S.ABCD có cạnh đáy bằng $a$ và cạnh bên tạo với đáy một góc bằng ${30^0}$. Thể tích của hình chóp S.ABCD là?

A. $\dfrac{{\sqrt 6 }}{3}{a^3}$            B. $\dfrac{1}{{18}}{a^3}$ 

C. $\dfrac{{\sqrt 6 }}{{18}}{a^3}$            D. $\dfrac{{\sqrt 6 }}{6}{a^3}$

Câu 15: Hình chóp đều S.ABC có cạnh đáy bằng $a$ và cạnh bên bằng $3a$. Thể tích hình chóp S.ABC là ?

A.$\dfrac{{\sqrt {28} }}{4}{a^3}$    B. $\dfrac{{\sqrt {26} }}{4}{a^3}$

C. $\dfrac{{\sqrt 3 }}{{12}}{a^3}$     D.  $\dfrac{{\sqrt {26} }}{{12}}{a^3}$

 Câu 16. Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a là:

A. $\dfrac{{{a^3}\sqrt 2 }}{3}$     B. $\dfrac{{{a^3}\sqrt 3 }}{6}$

C. $\dfrac{{{a^3}\sqrt 3 }}{2}$     D. $\dfrac{{{a^3}\sqrt 3 }}{4}$

Câu 17. Thể tích $V$ của khối lập phương $ABCD.A'B'C'D'$, biết $AB = 2a$  là:

A. $6{a^3}$ .        B. $2{a^3}$ .

 C. $\dfrac{{8{a^3}}}{3}$        D. $8{a^3}$

Câu 18. Cho lăng trụ $ABCD.A_1B_1C_1D_1$ , đáy là hình chữ nhật ,AB = a ,$AD = a\sqrt 3$. Hình chiếu vuông góc của $A_1$ trên mp(ABCD) trùng với giao điểm của AC và BD. Góc giữa $(ADD_1A_1)$ và (ABCD) bằng $60^o$ .Tính thể tích khối lăng trụ đã cho:   

A.$3\sqrt 3 {a^3}\quad$     B. $\dfrac{{3{a^3}}}{2}$

C.$\dfrac{{\sqrt 3 {a^3}}}{2}$         D.$\dfrac{{\sqrt 3 {a^3}}}{4}$

Câu19:  Số mặt phẳng đối xứng của hình hộp chữ nhật mà không có mặt nào là hình vuông:

A. 6              B. 2         

C. 3              D. 4

Câu 20: Hình nào trong các hình sau không phải là hình đa diện?

A. Hình thoi

B. Hình chóp

C. Hình lập phương

D. Hình lăng trụ

Lời giải chi tiết

Câu	1	2	3	4	5
Đáp án	C	A	A	D	C
Câu	6	7	8	9	10
Đáp án	A	D	A	B	A
Câu	11	12	13	14	15
Đáp án	C	C	A	C	D
Câu	16	17	18	19	20
Đáp án	C	D	B	C	A

Câu 1

Một hình chóp có 28 cạnh sẽ có 15 cạnh.

Chọn đáp án C.

Câu 2

Chọn đáp án A.

Câu 3

Ta có: $\left\{ \begin{array}{l}2SA' = 3AA' = 3\left( {SA - SA'} \right)\\3SB' = BB' = SB - SB'\end{array} \right.$

$\Rightarrow \left\{ \begin{array}{l}5SA' = 3SA\\4SB' = SB\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}\dfrac{{SA'}}{{SA}} = \dfrac{3}{5}\\\dfrac{{SB'}}{{SB}} = \dfrac{1}{4}\end{array} \right.$

Khi đó $\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}} = \dfrac{3}{5}.\dfrac{1}{4} = \dfrac{3}{{20}}$

Chọn đáp án A.

Câu 4

Thể tích của khối hộp chữ nhật ABCDA’B’C’D’ là $V = abc$

Chọn đáp án D.

Câu 5

Ta có: $V = b.h$

${V_{A'.ABC}} = \dfrac{1}{3}.Bh$

Chọn đáp án C.

Câu 6

Số đỉnh của một hình bát diện đều là 6.

Chọn đáp án A.

Câu 7

Thể tích khối chóp là $V = \dfrac{1}{3}.4.1,5 = 2\,\left( {{m^3}} \right)$

Chọn đáp án D.

Câu 8

Diện tích đáy của khối chóp là $S = \left( {a\sqrt 6 } \right)\left( {a\sqrt 6 } \right) = 6{a^2}$

Khi đó $h = \dfrac{{3V}}{S} = \dfrac{{6{a^3}}}{{6{a^2}}} = a$

Chọn đáp án A.

Câu 9

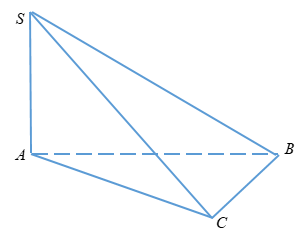
Hai mặt bên $\left( {SAB} \right)$ và $\left( {SAC} \right)$ cùng vuông góc với đáy

$\Rightarrow SA \bot \left( {ABC} \right)$

Áp dụng định lí Py – ta – go ta có:

$SA = \sqrt {S{C^2} - A{C^2}}  = \sqrt {3{a^2} - {a^2}}  = a\sqrt 2$

Khi đó:

$V = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.a\sqrt 2 .\dfrac{1}{2}a.a.\sin {60^0} = \dfrac{{{a^3}\sqrt 6 }}{{12}}$

Chọn đáp án B.

Câu 10

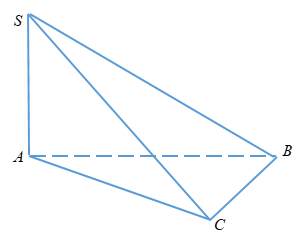
Gọi H là trung điểm của BC

(SBC) hợp với đáy (ABC) một góc 60^o

$\Rightarrow \widehat {SHA} = {60^0}$

Ta có: $AH = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}$

+ $\tan {60^0} = \dfrac{{SA}}{{AH}} \Rightarrow SA = \dfrac{{3a}}{2}$

Khi đó: $V = \dfrac{1}{3}.SA.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{3a}}{2}.\dfrac{1}{2}.a.a.\sin {60^0} = \dfrac{{{a^3}\sqrt 3 }}{8}$

Chọn đáp án A.

Câu 11

Ta có: $AH = DH = \dfrac{{AD}}{2} = a$

Áp dụng định lí Py – ta – go ta có:

$SH = \sqrt {S{A^2} - A{H^2}}  = \sqrt {5{a^2} - {a^2}}  = 2a$

Khi đó ta có:

$V = \dfrac{1}{3}.SH.{S_{ABCD}} = \dfrac{1}{3}.2a.2a.a = \dfrac{{4{a^3}}}{3}$

Chọn đáp án C.

Câu 12

Gọi O là giao điểm của AC và BD

Hình chóp có các cạnh bên bằng nhau nên chân đường vuông góc kẻ từ S xuống mặt phẳng (ABCD) là điểm O

Hay $SO \bot \left( {ABCD} \right)$

Ta có: $BD = \sqrt {A{B^2} + A{C^2}}  = \sqrt {9{a^2} + 16{a^2}}  = 5a$

+ $SO = \sqrt {S{D^2} - O{D^2}}  = \sqrt {25{a^2} - \dfrac{{25{a^2}}}{4}}  = \dfrac{{5a\sqrt 3 }}{2}$

Khi đó ta có:

$V = \dfrac{1}{3}.SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{5a\sqrt 3 }}{2}.3a.4a = 10{a^3}\sqrt 3$

Chọn đáp án C.

Câu 13

Chọn đáp án A.

Câu 14

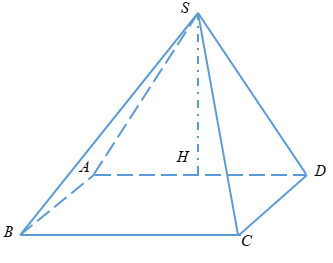
Gọi O là giao điểm của AC và BD

Các mặt bên đều tạp với đáy một góc bằng nhau nên $SO \bot \left( {ABCD} \right)$

Ta có: $BD = \sqrt {{a^2} + {a^2}}  = a\sqrt 2$

$\Rightarrow BO = DO = \dfrac{{a\sqrt 2 }}{2}$

+ $\tan {30^0} = \dfrac{{SO}}{{OB}} \Rightarrow SO = \dfrac{{\sqrt 3 }}{3}.\dfrac{{a\sqrt 2 }}{2} = \dfrac{{a\sqrt 6 }}{6}$

Khi đó ta có:

$V = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{6}.{a^2} = \dfrac{{{a^3}\sqrt 6 }}{{18}}$

Chọn đáp án C.

Câu 15

Gọi H là giao điểm của các đường cao trong tam giác ABC

Vì là hình chóp đều nên chân đường cao hạ từ S xuống mặt phẳng (ABC) chính là H

Hay $SH \bot \left( {ABC} \right)$

Ta có: $AH = \dfrac{2}{3}\sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{3}$

$\Rightarrow SH = \sqrt {S{A^2} - A{H^2}}  = \sqrt {9{a^2} - \dfrac{{{a^2}}}{3}}  = \dfrac{{a\sqrt {78} }}{3}$

Khi đó

$V = \dfrac{1}{3}SH.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{a\sqrt {78} }}{3}.\dfrac{1}{2}.aa\sin {60^0}$$\,= \dfrac{{{a^3}\sqrt {26} }}{{12}}$

Chọn đáp án D.

Câu 16

Diện tích đáy là: $S = \dfrac{1}{2}a.a\sin {60^0} = \dfrac{{{a^2}\sqrt 3 }}{4}$

Thể tích được xác định: $V = S.h = \dfrac{{{a^2}\sqrt 3 }}{4}.2a = \dfrac{{{a^3}\sqrt 3 }}{2}$

Chọn đáp án C.

Câu 17

Thể tích khối lập phương là $V = {\left( {2a} \right)^3} = 8{a^3}$

Chọn đáp án D.

Câu 18

Gọi H là trung điểm của AD

Góc giữa $\left( {ADD'A'} \right)$và (ABCD) bằng 60⁰

$\Rightarrow \widehat {A'HO} = {60^ \circ }$

Ta có:

$\tan {60^ \circ } = \dfrac{{A'O}}{{OH}} \Rightarrow AO' = \tan {60^ \circ }.\dfrac{a}{2} = \dfrac{{a\sqrt 3 }}{2}$

Vậy $V = A'O.{S_{ABCD}} = \dfrac{{a\sqrt 3 }}{2}.a.a\sqrt 3  = \dfrac{{3{a^3}}}{2}$

Chọn đáp án B.

Câu 19

Chọn đáp án C.

Câu 20

Hình thoi không phải là hình đa diện.

Chọn đáp án A.

 HocTot.Nam.Name.Vn