Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 1 - Hình học 7

Đề bài

Bài 1.Cho hình vẽ, biết:

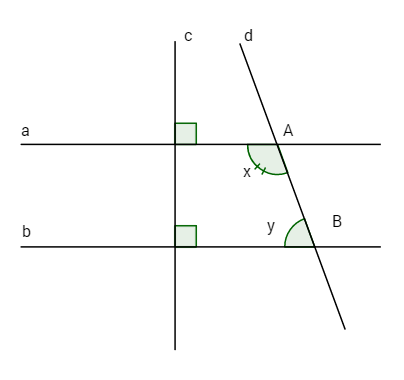
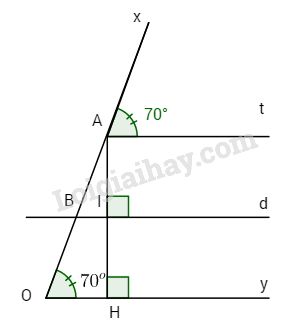
\(\widehat {tOB} + \widehat {OBy} = {180^o}\);\(\;a \bot c\,;\,b \bot c\) và \({x \over 5} = {y \over 4}\)

Tính x; y.

Bài 2. Cho \(\widehat {xOy} = {70^o}\). Trên tia Ox lấy A. Vẽ tia At sao cho \(\widehat {xAt} = {70^o}\)(tia At nằm trong góc \(\widehat {xOy}\))

a) Tia At có song song với Oy không? Vì sao?

b) Vẽ AH vuông Ay \(\left( {H \in Oy} \right)\). Chứng tỏ AH vuông góc với At.

c) Tính số đo góc \(\widehat {OAH}\).

d) Gọi I là trung điểm của AH. Đường trung trực d của đoan AH cắt OA tại B. Chứng tỏ \(\widehat {OBI} = \widehat {OAt}\).

Bài 3.Cho hình vẽ biết  Ax // By và \(\widehat {xAO} = {32^o}\) và \(\widehat {OBy} = {122^o}\)

Chứng tỏ \(OA \bot OB.\)

LG bài 1

Phương pháp giải:

+\(\left\{ \matrix{ a \bot c \hfill \cr b \bot c \hfill \cr}  \right. \Rightarrow a//b\)

+Nếu 1 đường thẳng cắt hai đường thẳng song song thì:

a) Các cặp góc so le trong bằng nhau.

b) Các cặp góc đồng vị  bằng nhau.

c) Các cặp góc trong cùng phía bù nhau

Lời giải chi tiết:

Bài 1.Ta có: \(\left\{ \matrix{ a \bot c \hfill \cr b \bot c \hfill \cr}  \right. \Rightarrow a//b\). Do đó \(x + y = {180^o}\)(cặp góc trong cùng phía).

Lại có \({x \over 5} = {y \over 4} = {{x + y} \over {4 + 5}} = {{{{180}^o}} \over 9} = {20^o}\)

\(\; \Rightarrow x = {100^o}\) và \(y = {80^o}.\)

LG bài 2

Phương pháp giải:

a.Chỉ ra 2 góc đồng vị bằng nhau

b.

\(\left\{ {\begin{array}{*{20}{c}}{a \bot b}\\{b//c}\end{array}} \right. \Rightarrow a \bot c\)

c. Tổng ba góc của 1 tam giác bằng 180 độ

d.\(\left\{ \matrix{ a \bot c \hfill \cr b \bot c \hfill \cr}  \right. \Rightarrow a//b\)

Lời giải chi tiết:

a) Hai góc \(\widehat {xAt}\) và \(\widehat {xOy}\) ở vị trí đồng vị, mà \(\widehat {xAt} = \widehat {xOy} = {70^o}\) nên At // Oy.

b) \(\left\{ \matrix{ AH \bot Oy \hfill \cr Oy//At\,(cmt) \hfill \cr}  \right. \Rightarrow AH \bot At.\)

c) Ta có: \(\widehat {xAt} + \widehat {tAH} + \widehat {HAO} = {180^o}\)

\(\eqalign{&  \Rightarrow \widehat {OAH} = {180^o} - \left( {\widehat {xAt} + \widehat {tAH}} \right)  \cr &  \Rightarrow \widehat {OAH} = {180^o} - \left( {{{70}^o} + {{90}^o}} \right)  \cr &  \Rightarrow \widehat {OAH} = {180^o} - {160^o} \cr&\Rightarrow \widehat {OAH} = {20^o} \cr} \)

d) Ta có: \(\left\{ \matrix{ d \bot AH \hfill \cr AH \bot At\,(cmt) \hfill \cr}  \right. \Rightarrow d//At.\)

LG bài 3

Phương pháp giải:

+\(\left\{ {\begin{array}{*{20}{c}}{a//b}\\{b//c}\end{array}} \right. \Rightarrow a//c\)

+Nếu 1 đường thẳng cắt hai đường thẳng song song thì:

a) Các cặp góc so le trong bằng nhau.

b) Các cặp góc đồng vị  bằng nhau.

c) Các cặp góc trong cùng phía bù nhau

Lời giải chi tiết:

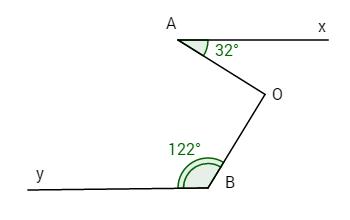
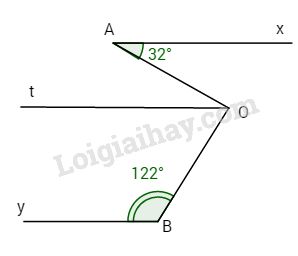
Kẻ qua O tia Ot // Ax (1).Hai góc \(\widehat {OBI}\) và \(\widehat {OAt}\) ở vị trí đồng vị \( \Rightarrow \widehat {OBI} = \widehat {OAt}.\)

Ta có \(\widehat {OAt} = \widehat {xAO} = {32^o}\)(cặp góc so le trong).

Lại có Ax // By (2). Từ (1) và (2) \( \Rightarrow Ot//By\), mà hai góc \(\widehat {tOB}\) và \(\widehat {OBy}\) ở vị trí trong cùng phía nên \(\widehat {tOB} + \widehat {OBy} = {180^o}\)

\(OA \bot OB.\) \( \Rightarrow \widehat {tOB} = {180^o} - \widehat {OBy} \)\(\;= {180^o} - {122^o} = {58^o}\).

Tia Ot nằm giữa hai tia OA và OB, ta có \(\widehat {AOt} + \widehat {tOB} = \widehat {AOB}\)

Hay

\(\eqalign{ & \widehat {AOB} = {32^o} + {58^o}  \cr & \widehat {AOB} = {90^o}. \cr} \)

Chứng tỏ \(OA \bot OB.\)

HocTot.Nam.Name.Vn