Đề kiểm tra 45 phút (1 tiết) - Đề số 1 - Chương 1 - Hình học 7

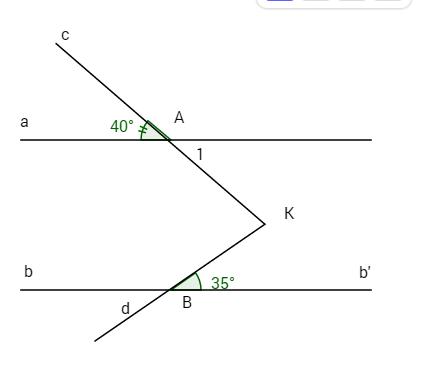
Đề bài

Bài 1.Cho hình vẽ, biết a//b.

C cắt a tại A sao cho \(\widehat {{\rm{cAa}}} = {40^o}\)

A cắt b tại B, sao cho \(\widehat {KBb'} = {35^o}\)

c cắt d tại K. Tính góc AKB

Bài 2. Cho hình vẽ.Tính góc  \(\widehat {AKB}\).

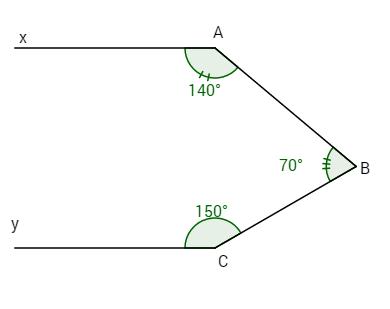
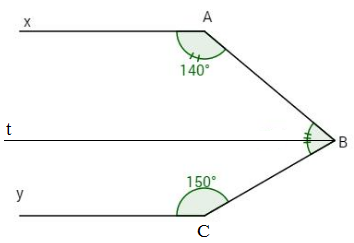
Biết  \(\widehat A = {140^o}\)

\(\widehat B = {70^o}\)

\(\widehat C = {150^o}\).

Chứng minh rằng Ax//Cy.

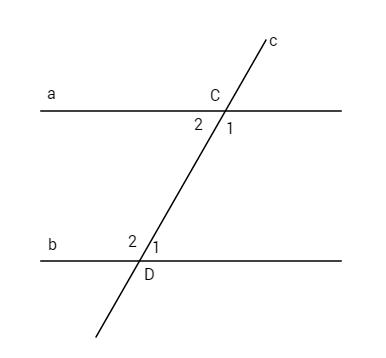
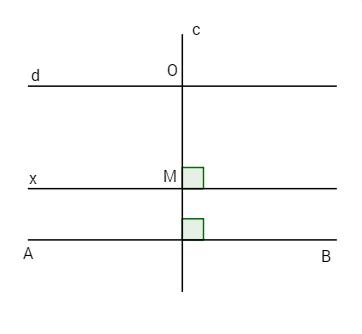
Bài 3. Cho đường thẳng AB lấy điểm O nằm ngoài đường thẳng AB. Qua O vẽ đường thẳng c vuông góc với AB và đường thẳng d song song với AB.

a) Đường thẳng d có vuông góc với đường thẳng c không? Vì sao?

b) Lấy M thuộc đường thẳng c (M khác O), vẽ đường thẳng x qua M và x vuông góc với đường thẳng c. Chứng tỏ x//d.

Bài 4. Cho hình vẽ, biết a//b và \(\widehat {{C_1}} - \widehat {{D_1}} = {30^o}\). 

Tính \(\widehat {{C_2}}\) và \(\widehat {{D_2}}\).

Phương pháp giải:

Nếu 1 đường thẳng cắt hai đường thẳng song song thì:

a) Các cặp góc so le trong bằng nhau.

b) Các cặp góc đồng vị  bằng nhau.

c) Các cặp góc trong cùng phía bù nhau 

LG bài 1

Lời giải chi tiết:

Bài 1. Ta có \(\widehat {{A_1}} = \widehat {{\rm{cAa}}} = {40^o}\) (đối đỉnh)

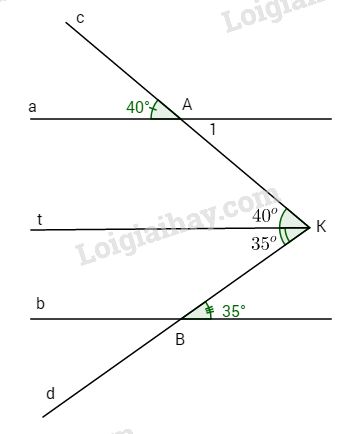
Lại có a // b \( \Rightarrow Kt//b\) (hai đường thẳng phân biệt cùng song song với đường thứ ba thì chúng song song vói nhau), hai góc \(\widehat {tKB}\) và \(\widehat {KBb'}\) ở vị trí so le trong. Kẻ qua K tia Kt // a, ta có \( \Rightarrow Kt//b\) \(\widehat {AKt} = \widehat {{A_1}} = {40^o}\) (cặp góc so le trong).

\( \Rightarrow \widehat {tKB} = \widehat {KBb'} = {35^o}.\)

 ta có \(\widehat {AKB} = \widehat {AKt} + \widehat {tKB}\)

\( = {40^o} + {35^o} = {75^o}.\)

LG bài 2

Lời giải chi tiết:

Kẻ qua B tia Bt // Ax (1), ta có \(\widehat {xAB} + \widehat {ABt} = {180^o}\)(cặp góc trong cùng phía)

\( \Rightarrow \widehat {ABt} = {180^o} - \widehat {xAB}\)

\( = {180^o} - {140^o} = {40^o}.\)

Mặt khác, vì Bt nằm giữa hai tia BA và BC nên ta có \(\widehat {ABt} + \widehat {tBC} = \widehat {ABC}\)

\( \Rightarrow \widehat {tBC} = {70^o} - {40^o} = {30^o}\)

Hai góc \(\widehat {tBC}\) và \(\widehat {BCy}\) ở vị trí trong cùng phía,

Mà \( \Rightarrow \widehat {tBC} + \widehat {BCy} = {30^o} + {150^o} = {180^o}\). Do đó Bt // Cy (2).

Từ (1) và (2) \( \Rightarrow \) Ax // Cy.

LG bài 3

Lời giải chi tiết:

Bài 3.

a)\(\left\{ \matrix{ c \bot AB \hfill \cr d//AB \hfill \cr}  \right. \Rightarrow d \bot c\) (nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia).

b) \(\left\{ \matrix{ x \bot c \hfill \cr c \bot d \hfill \cr}  \right. \Rightarrow x//d\) (hai đường thẳng phân biệt cùng vuông góc với đường thứ ba thì chúng song song với nhau). 

LG bài 4

Lời giải chi tiết:

Bài 4. Ta có a//b, \(\widehat {{D_2}} = \widehat {{C_1}}\) (hai góc so le trong)

\(\widehat {{C_1}}\) và \(\widehat {{D_1}}\) là hai góc trong cùng phía nên

\( \Rightarrow \widehat {{C_1}} + \widehat {{D_1}} = {180^o}\), lại có \(\widehat {{C_1}} - \widehat {{D_1}} = {30^o}\)

\( \Rightarrow 2\widehat {{C_1}} = {210^o} \Rightarrow \widehat {{C_1}} =210^0:2= {105^o}\)

\(\widehat {{C_2}} = {180^o} - \widehat {{C_1}}\)(cặp góc kề bù)\( = {180^o} - {105^o} = {75^o}\)

\(\widehat {{D_2}} = \widehat {{C_1}} = {105^o}\).

HocTot.Nam.Name.Vn