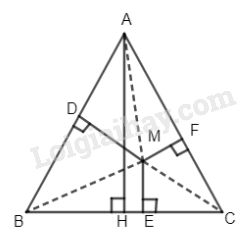
Đề kiểm tra 15 phút - Đề số 5 - Bài 3 - Chương 2 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 3 - Chương 2 - Hình học 8 Đề bài Cho tam giác đều ABC. Một điểm M thuộc miền trong của tam giác. Kẻ \(MD \bot AB,ME \bot BC,MF \bot AC.\) Chứng minh rằng: Tổng MD + ME + MF không phụ thuộc vào vị trí điểm M. Phương pháp giải - Xem chi tiết Sử dụng: Diện tích tam giác bằng nửa tích đường cao với cạnh đáy tương ứng Lời giải chi tiết
Ta có \({S_{ABC}} = {S_{AMB}} + {S_{BMC}} + {S_{CMA}}\) Hay \(\dfrac{1}{2}BC.AH = \dfrac{1}{2}AB.MD\)\(\, + \dfrac{1}{2}BC.ME + \dfrac{1}{2}AC.MF\) \( \Rightarrow \dfrac{1}{2}BC.AH = \dfrac{1}{2}BC\left( {MD + ME + MF} \right)\) \(\Rightarrow AH = MD + ME + MF\) AH không đổi nên tổng MD + ME + MF không đổi. HocTot.Nam.Name.Vn
|