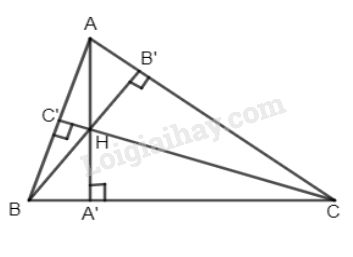
Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 2 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 2 - Hình học 8 Đề bài Cho tam giác ABC, các đường cao \(AA',BB',CC'\) cắt nhau tại H. Chứng minh rằng: a) \(\dfrac{{{S_{HBC}}}}{{{S_{ABC}}}} = \dfrac{{HA'}}{{AA'}}\) b) \(\dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}} = 1.\) Phương pháp giải - Xem chi tiết Sử dụng: Diện tích tam giác bằng nửa tích đường cao với cạnh đáy tương ứng Lời giải chi tiết
a) Ta có: \({S_{HBC}} = \dfrac{1}{2}BC.HA';\) \({S_{ABC}} = \dfrac{1}{2}BC.AA'\) \( \Rightarrow \dfrac{{{S_{HBC}}}}{{{S_{ABC}}}} = \dfrac{{HA'}}{{AA'}}\) b) Chứng minh tương tự câu a) ta có: \(\dfrac{{{S_{HAC}}}}{{{S_{ABC}}}} = \dfrac{{HB'}}{{BB'}}\) và \(\dfrac{{{S_{HAB}}}}{{{S_{ABC}}}} = \dfrac{{HC'}}{{CC'}}\) Do đó: \(\dfrac{{{S_{HBC}} + {S_{HAC}} + {S_{HAB}}}}{{{S_{ABC}}}} \)\(\,= \dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}}\) Hay \(1 = \dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}}\) (đpcm) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
