Đề kiểm tra 15 phút - Đề số 6 - Bài 2 - Chương 3 – Hình học 7

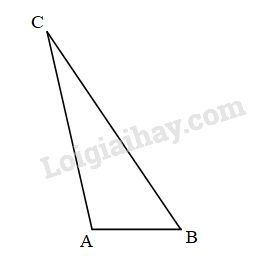
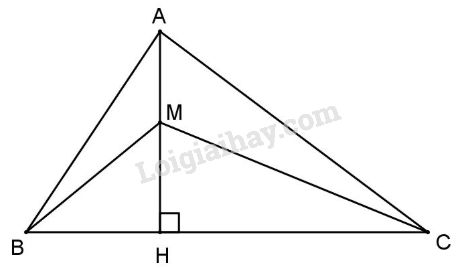
Đề bài

Bài 1: Cho tam giác ABC  có $\widehat B = 3\widehat C$ và $\widehat A = {100^0}$, hãy so sánh 3 cạnh của tam giác.

Bài 2: Cho tam giác ABC có $AB < AC$, kẻ AH vuông góc với BC

a) So sánh HB và HC.

b) Lấy M trên AH so sánh MB và MC.

c) So sánh $\widehat {BAH}$ và $\widehat {CAH}$. 

LG bài 1

Phương pháp giải:

+Tổng 3 góc của 1 tam giác bằng 180 độ

+ Trong 1 tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn

Lời giải chi tiết:

Ta có $\widehat A + 3\widehat C + \widehat C = {180^0}$ (định lý tổng 3 góc của tam giác) hay

$\eqalign{  & {100^0} + 4\widehat C = {180^0}  \cr  & 4\widehat C = {180^0} - {100^0} = {80^0}  \cr  & \widehat C = {20^0} \Rightarrow \widehat B = 3\widehat C = {3.20^0} = {60^0} \cr}$

Vậy $\widehat A > \widehat B > \widehat C{\rm{  }}({100^0} > {60^0} > {20^0})$

$\Rightarrow BC > AC > AB.$

LG bài 2

Phương pháp giải:

+Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:

a) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn

b) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn

+Tổng 3 góc của 1 tam giác bằng 180 độ

+Trong 1 tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn

Lời giải chi tiết:

a) $AB < AC{\;{  (gt) }}\Rightarrow HB < HC$ (quan hệ đường xiên và hình chiếu).

b) Vì $HB < HC$ (cmt) $\Rightarrow MB < MC$ (quan hệ đường xiên và hình chiếu).

c) Ta có $\Delta AHB$ vuông tại H (gt)

$\Rightarrow \widehat {BAH} + \widehat {ABC} = {90^0}$ 

Tương tự với $\Delta AHC$ ta có $\widehat {CAH} + \widehat {ACB} = {90^0}$

Mà $\widehat {ABC} > \widehat {ACB}$ ( vì $AB < AC$ gt)

$\Rightarrow \widehat {BAH} < \widehat {CAH}.$

HocTot.Nam.Name.Vn