Đề kiểm tra 15 phút - Đề số 8 - Bài 2 - Chương 3 – Hình học 7Giải Đề kiểm tra 15 phút - Đề số 8 - Bài 2 - Chương 3 – Hình học 7
Lựa chọn câu để xem lời giải nhanh hơn
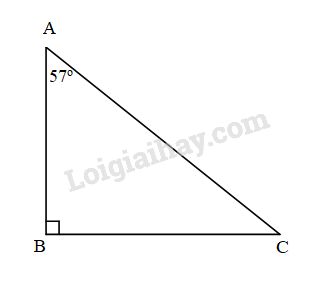
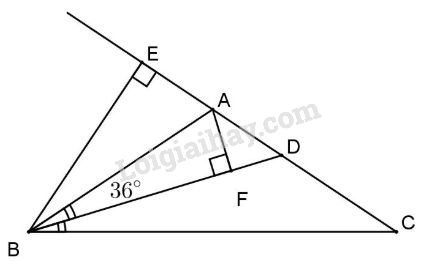
Đề bài Bài 1: Cho tam giác ABC vuông tại B có \(\widehat A = {57^0}\). Hãy so sánh các cạnh của tam giác ABC. Bài 2: Cho tam giác ABC cân tại A có \(\widehat {ABC} = {36^0}\). a) Tính số đo góc \(\widehat {BAC}\). b) Tia phân giác của góc ABC cắt cạnh AC tại D. Gọi E là hình chiếu của B lên CA và F là hình chiếu của A lên BD. Chứng minh \(\Delta ABE = \Delta ABF\). c) Chứng minh \(B{\rm{D}} < EC\). LG bài 1 Phương pháp giải: + Tổng ba góc của 1 tam giác bằng 180 độ + Trong tam giác cân 2 góc ở đáy bằng nhau +Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: a) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn b) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn Lời giải chi tiết:
Ta có \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng 3 góc của tam giác) LG bài 2 Lời giải chi tiết:
a) Ta có \(\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = {180^0}\) (tổng 3 góc của tam giác) mà \(\widehat {ABC} = \widehat {ACB}\) (\(\Delta ABC\) cân tại A) b) Ta có \(\widehat {BAC} + \widehat {BA{\rm{E}}} = {180^0}\) (kề bù) \( \Rightarrow \widehat {BA{\rm{E}}} = {180^0} - \widehat {BAC} \)\(\,= {180^0} - {108^0} = {72^0}.\) \(\Delta BA{\rm{E}}\) vuông tại E (gt) \( \Rightarrow \widehat {ABE} = {90^0} - {72^0} = {18^0}.\) BD là phân giác của góc \(\widehat {ABC}\) ta có: \(\widehat {AB{\rm{D}}} = \widehat {CB{\rm{D}}} = \dfrac{{\widehat {ABC}} }{ 2} =\dfrac {{{{36}^0}}}{2} = {18^0}.\) Xét \(\Delta {\rm A}{\rm B}{\rm E}\) và \(\Delta ABF\) có \(\widehat {A{\rm{E}}B} = \widehat {AFB}\) (cạnh huyền góc nhọn). c) Ta có \(B{\rm{D}} = BF + F{\rm{D}},CE = CA + A{\rm{E}}\) mà \(BF < BA = AC\) (quan hệ đường vuông góc và đường xiên). Tương tự: \(F{\rm{D}} < A{\rm{D}} = A{\rm{E}}\) \(\Rightarrow BF + F{\rm{D}} < AC + A{\rm{E}}\) hay \(B{\rm{D}} < EC.\) HocTot.Nam.Name.Vn
|