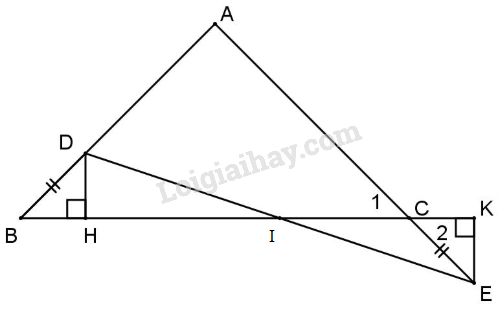
Đề kiểm tra 15 phút - Đề số 5 - Bài 2 - Chương 3 – Hình học 7

Đề bài

Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên tia đối của tia CA lấy điểm E sao cho $B{\rm{D}} = CE$, nối D với E, kẻ $DH \bot BC$ (H thuộc BC) CK vuông góc với đường thẳng BC (K thuộc BC). Chứng minh:

a) $BH = CK.$

b) $BC < DE.$ 

Lời giải chi tiết

a) Ta có $\widehat B = {\widehat C_1}$ (gt) và ${\widehat C_1} = {\widehat C_2}$ (đối đỉnh) $\Rightarrow \widehat B = {\widehat C_2}$.

Do đó hai tam giác vuông $\Delta BH{\rm{D}} = \Delta CKE$ (ch.gn)

$\Rightarrow BH = CK$.

b) Ta có $BC = BH + HC$

$HK = HC + CK$, mà $HB = CK$ (cmt)

$\Rightarrow BC = HK$.

Ta có $\Delta DHI$ vuông tại H nên $HI < DI$

Tương tự $IK < IE$

$\Rightarrow HI + IK < DI + IE$

Hay $HK < DE$, mà $HK = BC$, do đó $BC < DE$.  

HocTot.Nam.Name.Vn