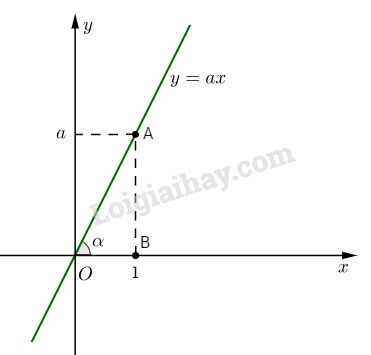
Đề kiểm tra 15 phút - Đề số 5 - Bài 5 - Chương 2 - Đại số 9Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 5 - Chương 2 - Đại số 9 Đề bài Bài 1. Viết phương trình đường thẳng (d) qua gốc tọa độ và tạo với trục hoành một góc \(60^\circ \) Bài 2. Tính góc \(α\) tạo bởi đường thẳng \(y = - {1 \over {\sqrt 3 }}x\) và trục hoành. Phương pháp giải - Xem chi tiết Vẽ đồ thị hàm số rồi tìm góc bằng cách sử dụng tỉ số lượng giác của góc nhọn. Đường thẳng \(y = ax +b(a ≠ 0)\) có hệ số góc là \(a\) Lời giải chi tiết Bài 1. Phương trình đường thẳng (d) qua \(O\) nên có dạng : \(y = ax (a ≠ 0)\). Cho \(x = 1 ⇒ y = a\). Vậy, ta có điểm \(A(1; a)\) thuộc (d). Trong tam giác vuông OAB (xem hình vẽ):
\(\tan \alpha = {{AB} \over {OB}} = {{\left| a \right|} \over 1} = \left| a \right|\) mà \(α = 60^\circ \) Vậy \(\tan 60^\circ = a ⇒ a = \sqrt 3 \) Vậy phương trình của (d) là : \(y = \sqrt 3 x\) Chú ý: - Ta có thể vẽ đường thẳng (d) : \(y = \sqrt 3 x\) bằng cách dựng một tia Ot sao cho \(\widehat {xOT} = 60^\circ \) (T có tung độ dương). Vậy đường thẳng (d) là đường thẳng chứa tia Ot. Tương tự: Vẽ đường thẳng \(y = {1 \over {\sqrt 3 }}x.\) Ta có: \(\tan \alpha = {1 \over {\sqrt 3 }} \Rightarrow \alpha = 30^\circ \) Dựng góc \(\widehat {TOx} = 30^\circ \) (T có tung độ dương). Từ đó dựng đường thẳng chứa tia \(OT\). Bài 2. Bảng giá trị:
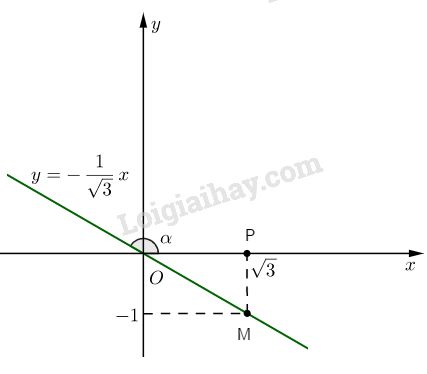
Đường thẳng \(y = - {1 \over {\sqrt 3 }}x\) qua hai điểm O(0; 0) và \(M\left( {\sqrt 3 ; - 1} \right)\)
Ta có : \(\alpha = \widehat {TOx}\) Trong tam giác \(OMP\), ta có: \(\eqalign{ & OP = \sqrt 3 ;MP = \left| { - 1} \right| = 1 \cr & \Rightarrow \tan \widehat {MOP} = {{MP} \over {OP}} = {1 \over {\sqrt 3 }} \cr&\Rightarrow \widehat {MOP} = 30^\circ \cr & \Rightarrow \widehat {TOx} = 150^\circ \,\,hay\,\,\alpha = 150^\circ \cr} \) HocTot.Nam.Name.Vn
|