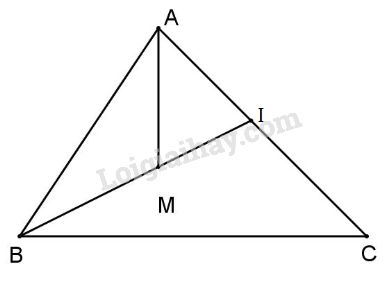
Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 3 – Hình học 7Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 3 – Hình học 7 Đề bài Cho tam giác ABC, điểm M nằm trong tam giác. Gọi I là giao điểm của BM và AC. Chứng minh rằng: MA+MB<IA+IB<CA+CB. Phương pháp giải - Xem chi tiết Trong một tam giác độ dài 1 cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại Lời giải chi tiết
Xét ΔAMI, theo bất đẳng thức tam giác MA<MI+IA⇒MA+MB<MI+IA+MB⇒MA+MB<IA+IB(1) Xét ΔBIC, ta có IB<IC+BC ⇒IB+IA<IC+BC+IA⇒IB+IA<AC+BC(2) Từ (1) và (2) ta có MA+MB<IA+IB<AC+BC. HocTot.Nam.Name.Vn
|