Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 3 – Hình học 7Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 3 - Chương 3 – Hình học 7 Đề bài Cho tam giác ABC có AB>AC, tia phân giác của góc A cắt BC ở D. Trên đoạn thẳng AD lấy điểm E. Chứng minh rằng: AB−AC>EB−EC. Phương pháp giải - Xem chi tiết +Trong một tam giác độ dài 1 cạnh luôn lớn hơn hiệu độ dài hai cạnh còn lại Lời giải chi tiết
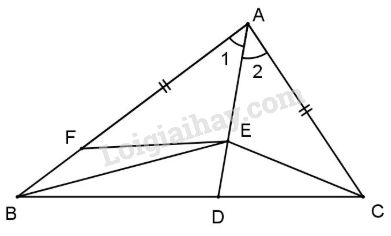
Vì AB>AC (gt) nên trên AB lấy điểm F sao cho AF=AC. Khi đó ΔAEF=ΔAEC (c.g.c) ⇒EF=EC. Xét ΔBEF, theo bất đẳng thức tam giác ⇒BF>BE−FE, mà BF=AB−AF ⇒AB−AF>EB−FE. Mặt khác AF=AC;FE=EC. Do đó AB−AC>EB−EC. HocTot.Nam.Name.Vn
|