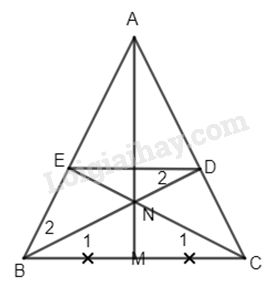
Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 1 - Hình học 8

Đề bài

Cho tam giác ABC cân ở A có M là trung điểm của BC. Trên tia AM lấy N. BN cắt AC ở D, CN cắt AB ở E. Chứng minh BEDC là hình thang cân.

Lời giải chi tiết

$\Delta ABC$ cân có AM là đường trung tuyến (gt) $\Rightarrow AM$ cũng là đường trung trực của BC.

N thuộc AM $\Rightarrow NB = NC$ hay $\Delta NBC$ cân tại N $\Rightarrow \widehat {{B_1}} = \widehat {{C_1}}$ 

Xét $\Delta BEC$ và $\Delta CDB$ có

$\widehat B = \widehat C$ (gt)

BC chung

$\widehat {{C_1}} = \widehat {{B_1}}(cmt)$

$\Rightarrow \Delta BEC = \Delta CDB(g.c.g)$

$\Rightarrow EB = DC$

Mà $AB = AC(gt)$ $\Rightarrow AB - EB = AC - DC$

Hay AE = AD.

Từ đó $\Delta AED$ cân tại A $\Rightarrow \widehat {AED} = \widehat {ADE} =\dfrac {{{{180}^ \circ } - \widehat A} }{2}$

Với $\Delta ABC$ có: $\widehat {ABC} = \widehat {ACB} = \dfrac{{{{180}^ \circ } - \widehat A} }{2}$ $\Rightarrow \widehat {AED} = \widehat {ABC}$

Do đó $ED// BC$ (cặp góc đồng vị bằng nhau) nên BEDC là hình thang.

Lại có $\widehat B = \widehat C$ (gt).

Vậy BEDC là hình thang cân.

HocTot.Nam.Name.Vn