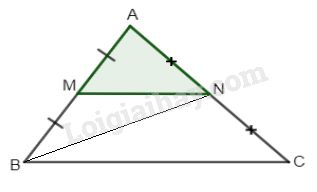
Đề kiểm tra 15 phút - Đề số 3 - Bài 3 - Chương 2 - Hình học 8

Đề bài

a) Cho tam giác ABC có M, N lần lượt là trung điểm của AB, AC. Chưng minh rằng: \({S_{ABC}} = 4{S_{AMN}}.\)

b) Cho \(\Delta ABC.\) Gọi \(A'B'C'\) lần lượt là trung điểm của BC, AC và AB. Biết diện tích của \(\Delta ABC\) là \(12c{m^2}\) . Tính \(S(A'B'C').\)

Lời giải chi tiết

a)

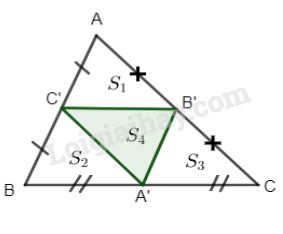
BN là trung tuyến của \(\Delta ABC\) nên

\({S_{ANB}} = {S_{BNC}} = {1 \over 2}{S_{ABC}}\) (chung đường cao, đáy tương ứng bằng nhau).

Tương tự NM là trung tuyến của \(\Delta ANB\) nên \({S_{AMN}} = {S_{BNM}} = {1 \over 2}{S_{ANB}}.\)

Do đó: \({S_{AMN}} = {1 \over 4}{S_{ABC}}\) hay \({S_{ABC}} = 4{S_{AMN}}.\) 

b) Ta có \(C'B',B'A',A'C'\) là các đường trung bình của \(\Delta ABC\) nên các tam giác sau đây bằng nhau:

\(\Delta AC'B' = \Delta A'B'C' = \Delta  C'BA' \)\(\,= \Delta B'A'C\left( {c.c.c} \right)\)

\( \Rightarrow {S_1} = {S_2} = {S_3} = {S_4} = {1 \over 4}{S_{ABC}}\)

Hay \({S_{A'B'C'}} = {1 \over 4}{S_{ABC}} = {{12} \over 4} = 3c{m^2}.\)

HocTot.Nam.Name.Vn