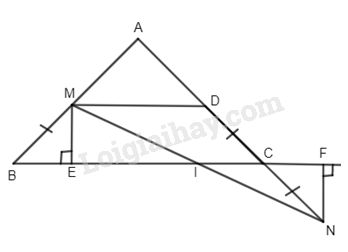
Đề kiểm tra 15 phút - Đề số 3 - Bài 3 - Chương 1 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 3 - Chương 1 - Hình học 8 Đề bài Tam giác ABC cân tại A, M là điểm bất kì nằm giữa hai điểm A và B. Trên tia đối của tia CA lấy N sao cho CN = BM. Vẽ ME và NF lần lượt vuông góc với đường thẳng BC. Gọi I là giao điểm của MN và BC. a) Chứng minh IE = IF. b) Trên cạnh AC lấy D sao cho CD = CN. Chứng minh BMDC là hình thang cân. Phương pháp giải - Xem chi tiết Sử dụng: Tứ giác có hai cạnh đối song song là hình thang Hình thang có hai góc ở đáy bằng nhau là hình thang cân. Lời giải chi tiết
a) Ta có \(\widehat B = \widehat C\) (do tam giác ABC cân tại A) mà \(\widehat C = \widehat {NCF}\) (đối đỉnh) Suy ra \(\widehat B = \widehat {NCF}\) Xét \(\Delta MEB\) và \(\Delta NFC\) có: +) BM=CN (gt) +) \(\widehat B = \widehat {NCF}\) Do đó \(\Delta MEB = \Delta NFC\) (cạnh huyền – góc nhọn) \( \Rightarrow ME = NF\) Lại có \(ME// NF\) (cùng vuông góc với BC) \( \Rightarrow \widehat {EMI} = \widehat {FNI}\) (so le trong) Xét \(\Delta IME\) và \(\Delta INF\) có: +) \(\widehat {EMI} = \widehat {FNI}\) (cmt) +) ME=NF (cmt) +) \(\widehat {MEI} = \widehat {NFI}=90^0\) Từ đó \(\Delta IME = \Delta INF(g.c.g) \Rightarrow IE = IF\) b) Ta có CD = CN mà CN = BM (gt) \( \Rightarrow BM = CD\) mà \(AB = AC\) \( \Rightarrow AB - BM = AC - CD\) hay AM = AD \( \Rightarrow \Delta AMD\) cân tại A nên: \(\widehat {AMD} = \widehat {ADM} = \dfrac{{{{180}^ \circ } - \widehat A}}{2}\) Mặt khác \(\Delta ABC\) cân tại A \( \Rightarrow \widehat {ABC} = \widehat {ACB} =\dfrac {{{{180}^ \circ } - \widehat A} }{2}\) Do đó \(\widehat {AMD} = \widehat {ABC} \Rightarrow MD//BC\) hay BMDC là hình thang có \(\widehat B = \widehat C\) Suy ra BMDC là hình thang cân. HocTot.Nam.Name.Vn
|