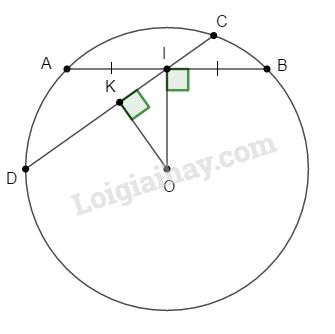
Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 2 - Hình học 9Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 2 - Hình học 9 GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn Đề bài Gọi I là trung điểm của dây cung AB không qua tâm của đường tròn (O; R). Qua I vẽ dây cung CD. a. Chứng tỏ CD≥AB. Tìm độ dài nhỏ nhất, lớn nhất của các dây quanh I. b. Cho R=5cm,OI=4cm. Tính độ dài dây cung ngắn nhất qua I. c. Chứng tỏ rằng : ^OAI>^ODI Phương pháp giải - Xem chi tiết - Trong hai dây của một đường tròn: a) Dây nào lớn hơn thì dây đó gần tâm hơn. b) Dây nào gần tâm hơn thì dây đó lớn hơn. - Định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương các cạnh góc vuông. - Sử dụng tỉ số lượng giác của góc nhọn.
Lời giải chi tiết
a. Kẻ OK⊥CD, ta có: ∆OKI vuông nên OI≥OK (cạnh huyền > cạnh góc vuông) ⇒CD≥AB (định lí 2) Dấu “=” xảy ra khi CD=AB. Do đó độ dài nhỏ nhất của CD bằng AB hay CD trùng với AB. Hiển nhiên đường kính qua I là dây lớn nhất. b. Ta có: ∆OIA vuông tại I ⇒AI=√OA2−OI2=√52−42=3(cm) Do đó dây cung AB=6cm c. sin^OAI=OIOA=OIR;sin^ODI=OKOD=OKR Mà OI>OK⇒OIR>OKR hay sin^OAI>sin^ODI⇒^OAI>^ODI HocTot.Nam.Name.Vn
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|