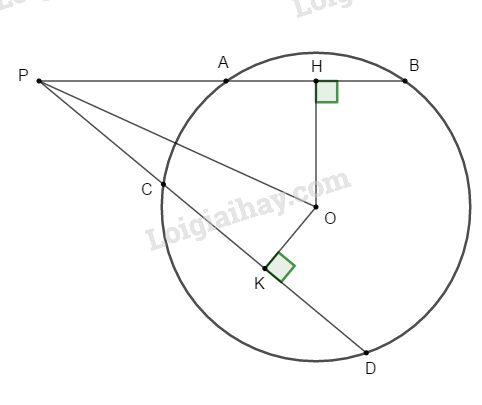
Đề kiểm tra 15 phút - Đề số 5 - Bài 3 - Chương 2 - Hình học 9

Đề bài

Cho điểm P nằm ngoài đường tròn (O; R) và $OP = 2R.$ Một đường thẳng qua P cắt (O) tại A và B ( A nằm giữa B và P) và $AB = R.$ Gọi H là chân đường vuông góc kẻ từ O đến PB.

a. Tính OH, AP theo R. 

b. Kẻ một đường thẳng khác qua P cắt (O) tại C và D (CD ở khác phía với AB so với OP), kẻ $OK ⊥ CD.$

So sánh AB và CD biết $OK < {{R\sqrt 3 } \over 2}$

Lời giải chi tiết

a. Ta có: $OH ⊥ AB$ (gt) 

$\Rightarrow HA = HB = {{AB} \over 2} = {R \over 2}$

(định lí đường kính dây cung)

Xét tam giác vuông AHO, ta có:

$OH = \sqrt {A{O^2} - A{H^2}}$$\;= \sqrt {{R^2} - {{\left( {{R \over 2}} \right)}^2}}  = {{R\sqrt 3 } \over 2}$

∆PHO vuông tại H, ta có:

$\eqalign{  & PH = \sqrt {P{O^2} - O{H^2}} \cr& = \sqrt {{{\left( {2R} \right)}^2} - {{\left( {{{R\sqrt 3 } \over 2}} \right)}^2}}  = {{R\sqrt {13} } \over 2}  \cr  &  \Rightarrow PA = PH - AH \cr&= {{R\sqrt {13} } \over 2} - {R \over 2} = {{R\left( {\sqrt {13}  - 1} \right)} \over 2} \cr}$

b. $OK < {{R\sqrt 3 } \over 2}$ hay $OK < OH = {{R\sqrt 3 } \over 2}\,\left( {cmt} \right)$

$\Rightarrow AB < CD$

HocTot.Nam.Name.Vn