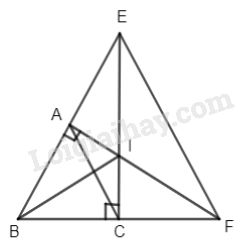
Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 1 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 1 - Hình học 8 Đề bài Cho tam giác đều ABC. Vẽ đường vuông góc với BC tại C cắt AB tại E. Vẽ đường vuông góc với AB tại A cắt BC tại F. Chứng minh ACFE là hình thang cân. Phương pháp giải - Xem chi tiết Tứ giác có hai cạnh đối song song là hình thang Hình thang có hai góc ở đáy bằng nhau là hình thang cân. Lời giải chi tiết
Gọi I là giao điểm của AF và CE. Ta có hai tam giác vuông BAI và BCI có AB=BC (do tam giác ABC đều), cạnh BI chung Suy ra ΔBAI=ΔBCI (cạnh huyền- cạnh góc vuông) ⇒IA=IC Xét hai tam giác vuông AIE và CIF, ta có: IA = IC (cmt) ^AIE=^CIF (đối đỉnh) ^IAE=^ICF=90∘ Suy ra ΔAIE=ΔCIF(g.c.g) ⇒AE=CF ( hai cạnh tương ứng) Mà BA = BC (gt) ⇒AE+BA=CF+BC hay BE = BF. Do đó ΔEBF cân có ˆB=60∘(gt) nên là tam giác đều ⇒ˆE=ˆF=60∘ ⇒ˆE=^BAC⇒AC//EF (cặp góc đồng vị bằng nhau) Suy ra ACFE là hình thang có ˆE=ˆF nên ACFE là hình thang cân. HocTot.Nam.Name.Vn
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|